1

Piotr LUDWIKOWSKI

2009/2010Fizyka

8 października 2009

Czwartek, 13:00

dr J. Rudzińska-Girulska

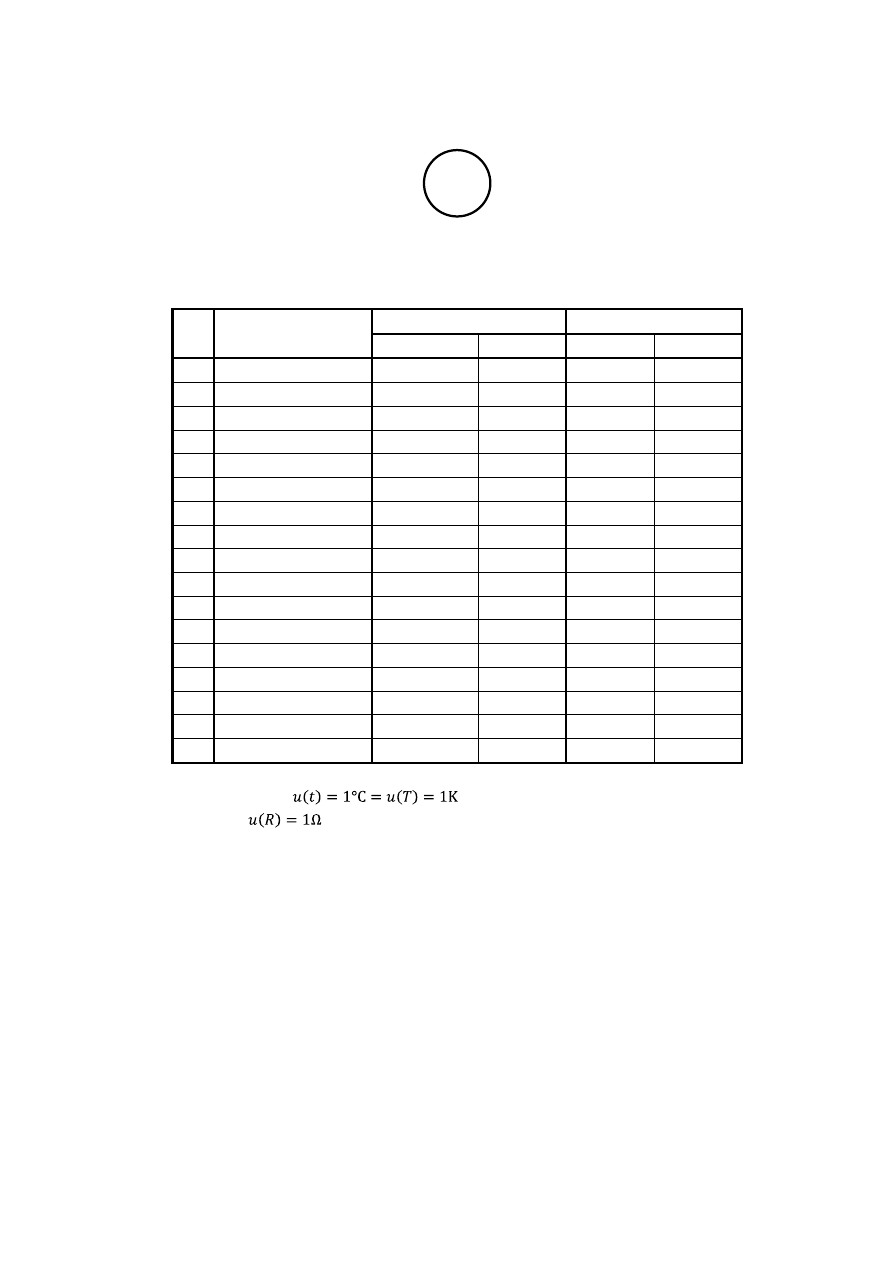
ZALEŻNOŚĆ OPORU ELEKTRYCZNEGO

METALU I PÓŁPRZEWODNIKA OD TEMPERATURY

Lp. Temperatura T, °C/K

Opór termistora R

1

[kΩ]

Opór miedzi R

2

[kΩ]

temp. ros.

temp. mal. temp. ros. temp. mal.

1

22/295

0,213

0,177

0,219

0,223

2

27/300

0,117

0,149

0,231

0,226

3

32/305

0,095

0,128

0,236

0,230

4

37/310

0,079

0,109

0,241

0,233

5

42/315

0,064

0,094

0,246

0,236

6

47/320

0,054

0,087

0,250

0,240

7

52/325

0,048

0,075

0,251

0,243

8

57/330

0,042

0,066

0,251

0,246

9

62/335

0,037

0,058

0,261

0,250

10

67/340

0,033

0,051

0,264

0,253

11

72/345

0,030

0,046

0,267

0,257

12

77/350

0,027

0,040

0,270

0,260

13

82/355

0,023

0,035

0,273

0,264

14

87/360

0,021

0,032

0,275

0,268

15

92/365

0,018

0,028

0,281

0,272

16

97/370

0,017

0,024

0,284

0,277

17

103/375

0,015

0,015

0,288

0,288

Niepewność pomiaru temperatury:

Niepewność pomiaru oporu:

57

2

TEORIA:

Opór

elektryczny

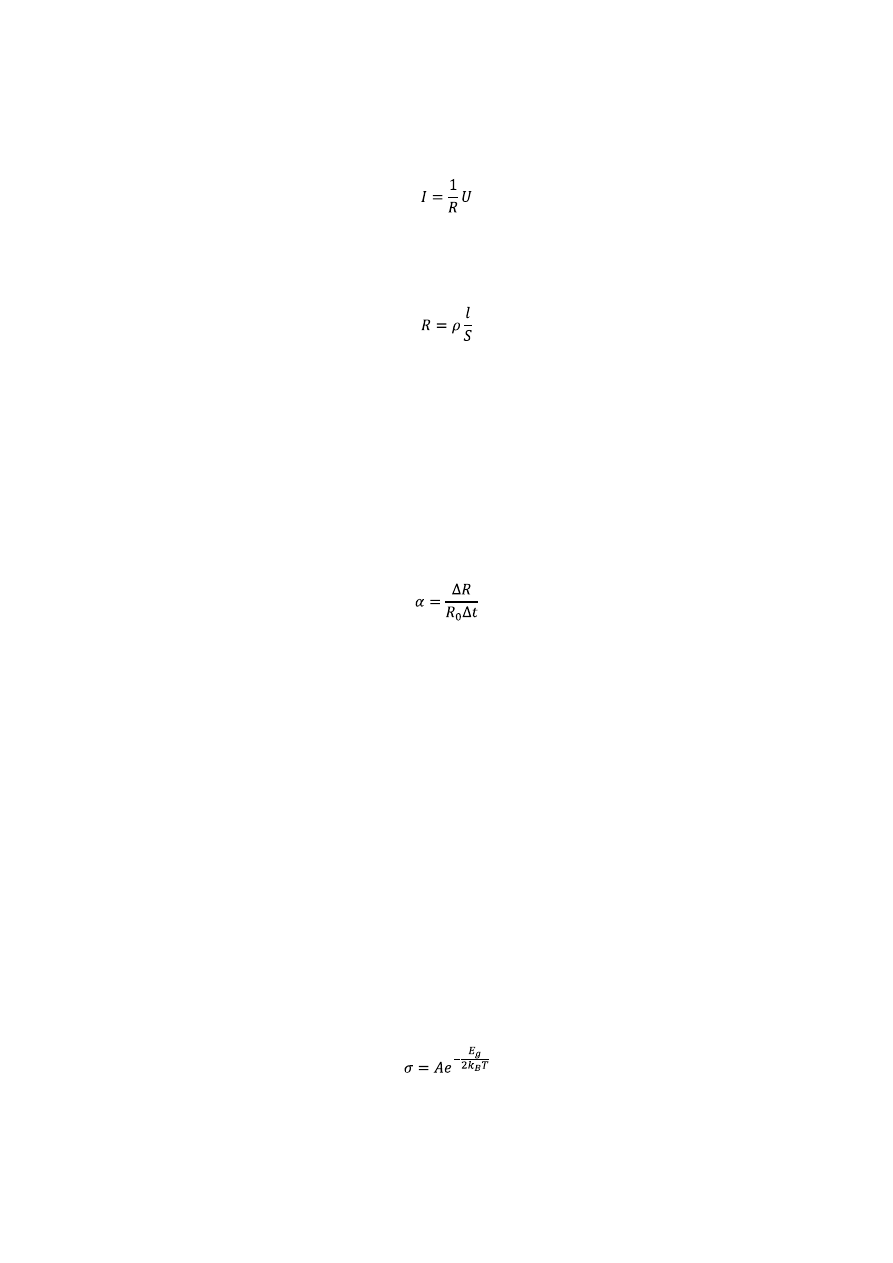
Zgodnie z I prawem Ohma natężenie prądu jest proporcjonalne do napięcia przyłożonego do końców

przewodnika i wyraża się wzorem:

Odwrotnością współczynnika proporcjonalności jest opór elektryczny. Oznaczamy go literą R i wyrażamy w

omach [Ω]. Warto wspomnieć, że wyrażenie to jest definicją oporu. Sens tej zależności jest taki, że wzrost napięcia
powoduje wzrost natężenia, czyli inaczej dla każdej pary wartości U i I stosunek U/I jest stały. Opór przewodnika jest

proporcjonalny do jego długości i odwrotnie proporcjonalny do przekroju poprzecznego:

Współczynnik proporcjonalności ρ nazywamy oporem właściwym. Jednostką jest jeden omometr

[1 Ωm].

Przewodnictwo w ciałach stałych

W ciałach stałych przewodzenie prądu jest możliwe dzięki ruchomym ładunkom. Napięcie przyłożone do

końców przewodnika powoduje uporządkowany ruch nośników tych ładunków (elektronów, jonów dodatnich i

ujemnych), które pod wpływem sił pola elektrycznego poruszają się z pewną prędkością v. W metalach, liczba

elektronów swobodnych, które są nośnikami prądu jest olbrzymia. Najczęściej są to elektrony walencyjne

poszczególnych atomów tworzących sieć krystaliczną.

Okazuje się, że opór jest stały dla danego przewodnika tylko przy stałej temperaturze. Jeżeli podczas

przepływu prądu ogrzewamy lub ochładzamy przewodnik, to możemy zaobserwować odpowiednio dodatnie lub

ujemne przyrosty oporu. Dla każdego przewodnika charakterystyczny jest współczynnik temperaturowy oporu α:

gdzie R

0

– opór przewodnika w temperaturze początkowej.

Pasma energetyczne kryształów, zależność przewodnictwa elektrycznego półprzewodników od temperatury

Przewodzenie prądu elektrycznego jest związane ze zmianą energii kinetycznej elektronów, które muszą być

przyspieszane przez pole elektryczne po to, aby uzyskać energię kinetyczną. W metalach puste poziomy

energetyczne znajdują się bardzo blisko poziomów zapełnionych, dlatego aby przejść na wyższy poziom

energetyczny elektrony potrzebują stosunkowo niewielkiej energii, co skutkuje tym, że nawet w niskich

temperaturach pole elektryczne może przyspieszać elektrony i nadawać im większą energię. Nośnikami są elektrony

z pasma walencyjnego, które można nazwać pasmem przewodzącym.

W półprzewodnikach puste i zapełnione poziomy energetyczne oddziela tzw. pasmo wzbronione (zakaz

Pauligo). Przy mniejszej szerokości pasma wzbronionego, część elektronów z pasma walencyjnego może w wyniku
wzbudzeń termicznych (zmiany energii) przedostać się do wyższego, pustego pasma energetycznego nawet w

temperaturze pokojowej. W paśmie tym, które w półprzewodnikach nazywane jest pasmem przewodnictwa,

elektrony mogą być przyspieszane polem elektrycznym, czyli mogą stać się nośnikami prądu. Dzięki zwolnieniu

niektórych poziomów w górnej części pasma walencyjnego, elektrony pozostałe w tym paśmie także uzyskują

możliwość brania udziału w przewodzeniu prądu. Przewodnictwo związane z ruchem elektronów w prawie

całkowicie zapełnionym paśmie walencyjnym, nosi nazwę przewodnictwa dziurowego. Przy podwyższaniu

temperatury półprzewodnika rośnie eksponencjalnie prawdopodobieństwo termicznego wzbudzenia elektronów do

pasma przewodnictwa, a wraz z nim koncentracja nośników prądu. Ponieważ przy wzroście temperatury ruchliwość

nośników prądu maleje znacznie wolniej niż wzrasta ich koncentracja, to w rezultacie, przy podwyższaniu

temperatury opór elektryczny półprzewodnika maleje (odwrotnie niż w przypadku metali). Zależność przewodności

właściwej σ półprzewodnika od temperatury T wyraża się wzorem:

gdzie: E

g

oznacza energię aktywacji nośników, k

B

– stała Boltzmanna, A –stała.

3

OPRACOWANIE WYNIKÓW
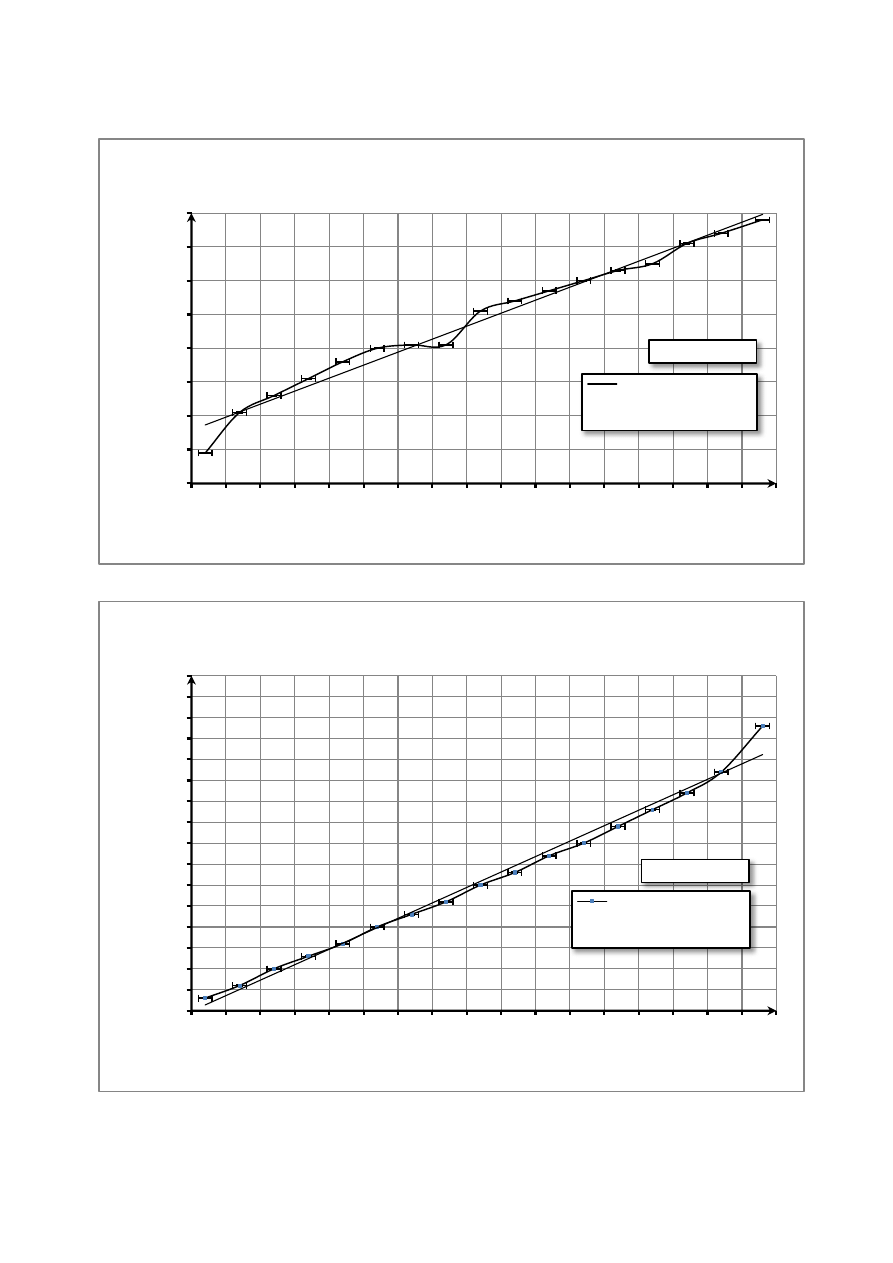
Najpierw sporządzam wykresy zależności oporu od temperatury dla drutu miedzianego i termistora:
I Wykres dla miedzi (temperatura rosnąca):

II Wykres dla miedzi (temperatura malejąca):

R = 7,69t + 2103

2100

2200

2300

2400

2500

2600

2700

2800

2900

20

25

30

35

40

45

50

55

60

65

70

75

80

85

90

95

100 105

Op

ó

r

[Ω

]

Temperatura [°C]

Wykres I.1

Zależność oporu drutu miedzianego od temperatury

Zależność oporu drutu
miedzianego od
temperatury

R = 7,38t + 2051

2200

2250

2300

2350

2400

2450

2500

2550

2600

2650

2700

2750

2800

2850

2900

2950

3000

20

25

30

35

40

45

50

55

60

65

70

75

80

85

90

95

100 105

Op

ó

r

[Ω

]

Temperatura [°C]

Wykres I.2

Zależność oporu miedzi od temperatury (temp. malejąca)

Zależność oporu
miedzi od temperatury
(temp. malejąca)

4

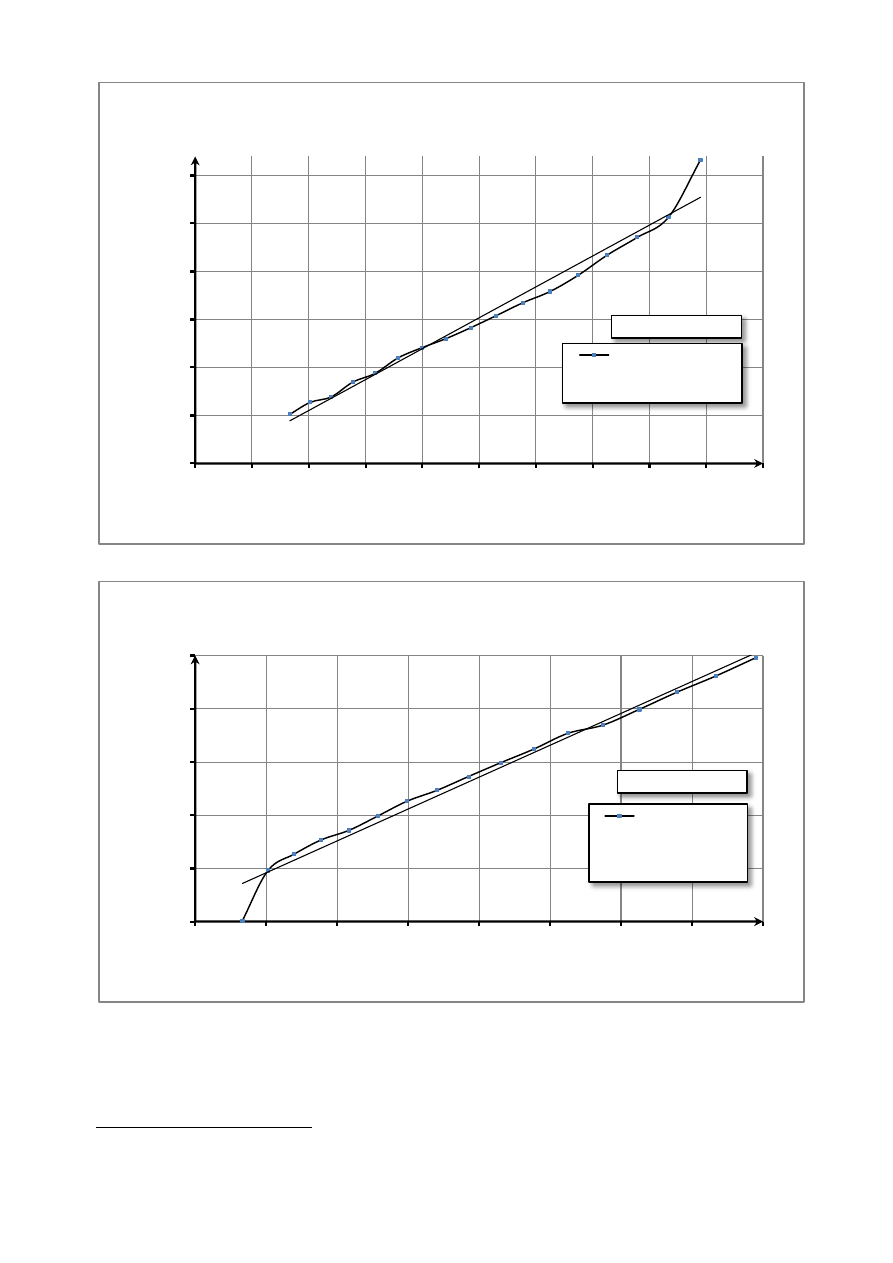
I Wykres dla termistora (temperatura rosnąca):

II Wykres dla termistora (temperatura malejąca):

Wartości temperaturowego współczynnika oporu dla miedzi (podobnie jak dla półprzewodnika) zostały

podane na każdym wykresie. Zobaczmy jak wyglądały obliczenia

1

:

1

Obliczenia dla każdego z czterech temperaturowych współczynników oporu zostały wykonane identycznie,

dlatego szczegółowe operacje przedstawię tylko na jednym przykładzie. Będzie to wykres I.1 (oporu od temp. dla miedzi).

ln R = 3221T

-1

- 3,64

4,500

5,000

5,500

6,000

6,500

7,000

7,500

0,00250 0,00260 0,00270 0,00280 0,00290 0,00300 0,00310 0,00320 0,00330 0,00340 0,00350

ln

R

Odwrotność temperatury *K

-1

]

Wykres II.1

Zależność oporu od temperatury dla termistora

Zależność oporu od
temperatury dla
półprzewodnika

ln R = 2994T

-1

- 2,63

5,000

5,500

6,000

6,500

7,000

7,500

0,00260

0,00270

0,00280

0,00290

0,00300

0,00310

0,00320

0,00330

0,00340

ln

R

Odwrotność temperatury *K

-1

]

Wykres II.2

Zależność oporu termistora od temperatury (temp.malejąca)

Zależność oporu
termistora od
temperatury
(temp.malejąca)

5

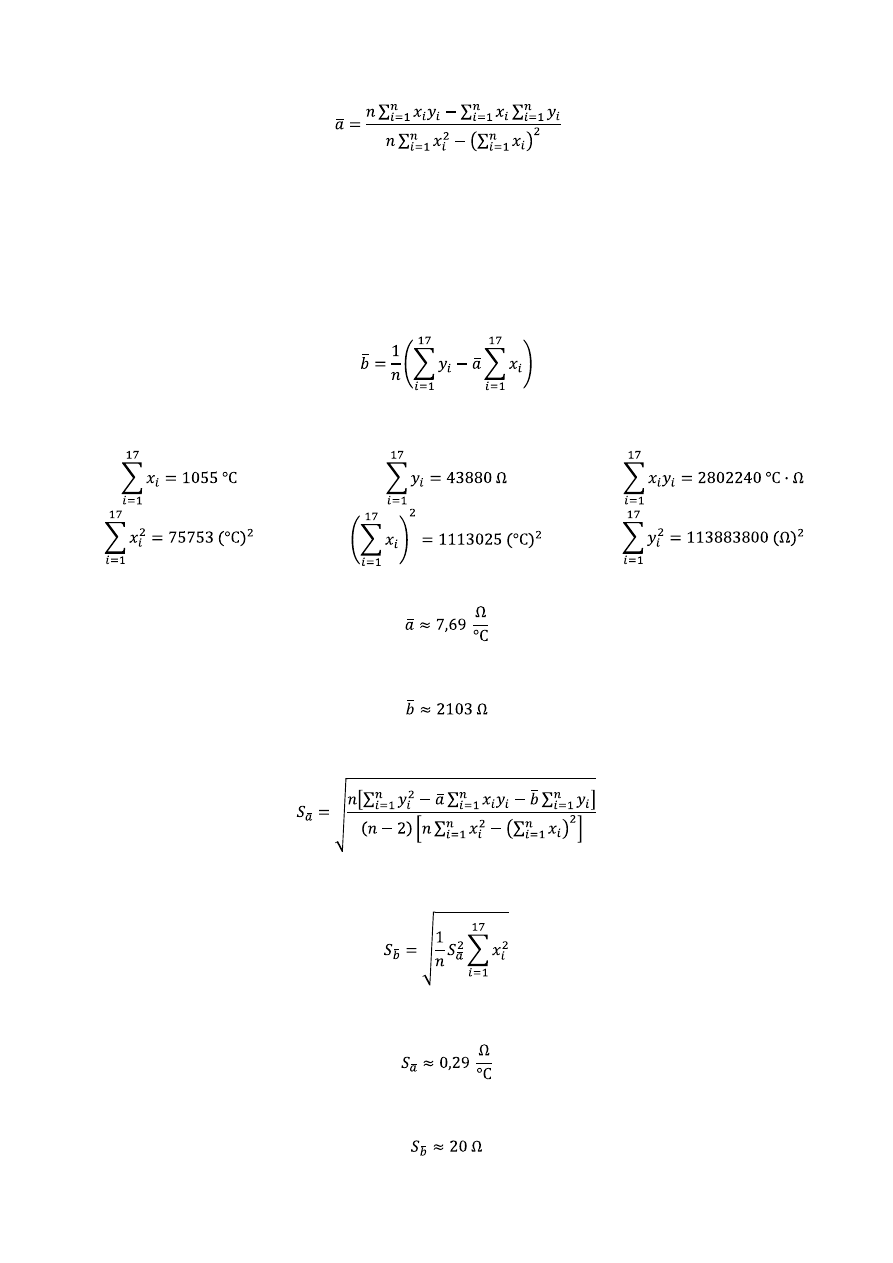
Aby wyliczyć współczynnik kierunkowy prostej (który jest jednocześnie temperaturowym współczynnikiem

oporu), korzystamy z następującego wzoru:

gdzie:
x

i

– temperatury poszczególnych pomiarów (dla badanego wykresu w °C),

y

i

– opory w poszczególnych pomiarach (w Ω),

n =17 – liczba pomiarów.

Obliczymy również współczynnik b dla prostej reprezentującej zależność oporu od temperatury:

Wyliczamy poszczególne składniki powyższych wzorów:

Następnie wstawiamy do wyrażeń i otrzymujemy:

oraz:

Do obliczenia niepewności posłużymy się wzorami:

oraz:

Otrzymujemy:

oraz:

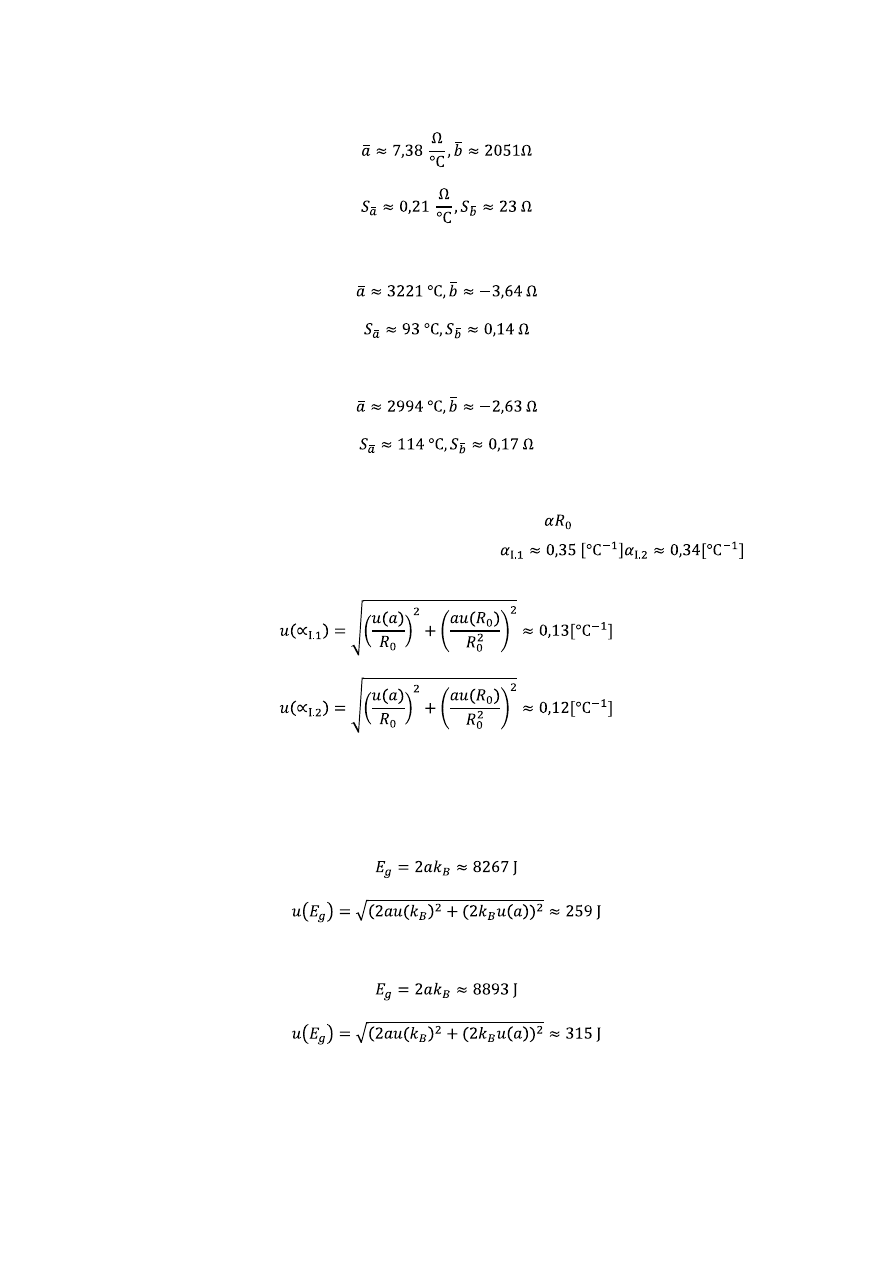
6

Dla pozostałych wykresów analogicznie:

Wykres I.2:

Wykres II.1:

Wykres II.2:

Otrzymane współczynniki kierunkowe prostych reprezentują iloczyn

, gdzie R

0

= 22°.

Temperaturowe współczynniki oporu α wynoszą odpowiednio

.

Niepewności policzymy z wzoru:

Wykresy II.1 i II.2 ilustrują zależność oporu od temperatury dla termistora. Policzymy jeszcze szerokość pasma

wzbronionego E

g

:

Wykres II.1:

Wykres II.2:

7

WNIOSKI

W wyniku przeprowadzonego eksperymentu otrzymaliśmy następujące wyniki: Temperaturowy

współczynnik oporu miedzi dla temp. rosnącej wyniósł

, a dla

temp. malejącej

. Wynik ten znacząco obiega od danych

tablicowych. Myślę, że może to być spowodowane złą jakością użytych przewodów. Świadczyć może o

tym również fakt, że oporu próbki manganinowej w ogóle nie udało się zmierzyć ze względu na zbyt
luźno dopasowany przewód.

Wielkość pasma wzbronionego dla półprzewodnika wyliczyliśmy na

.