Automatyka, sem. III ENS, rok akad. 2012/2013
Przykładowe zadania na kolokwium nr 1, 04. 12. 2012 r.
Zad. 1.
Wyznaczyć transmitancję operatorową układu, opisanego równaniem różniczkowym
u
u
u
y
y
y
5
3
2
2
przy założeniu, że w układzie panują zerowe warunki początkowe. Określić wartości zer i biegunów
układu. Wypowiedzieć się na temat stabilności układu o transmitancji uzyskanej z w/w równania.
Zad. 2.
Dany jest układ o odpowiedzi skokowej:
)
(
1
]
4
2
1
[
)
(
4
t
e
e
t
h
t
t
Znaleźć transmitancję układu oraz jego w przestrzeni stanu.
Zad. 3.
Dany jest układ dynamiczny, opisany w przestrzeni stanu za pomocą następujących równań:
)
(
6
2
)
(
0
)
0
(
);
(
1
1
)
(
3
0
0
2
)
(
t
x
t
y
x
t
u
t
x
t
x
Znaleźć i narysować odpowiedź skokową tego układu. Podać opis układu w przestrzeni fazowej.
Zad. 4.
Dla jakiej wartości parametru a odpowiedź impulsowa układu opisanego równaniem stanu:
)
(
5
4
)
(
0
)
0
(
);
(
1
0
)
(
3
1
0
)
(
t
x
t
y
x
t
u
t
x
a
t
x
ma postać:
)
(
1
]
4
[
)
(
2
t
e
e
t
g
t
t
Zad. 5.
Dany jest układ o transmitancji operatorowej:
)
3
(
)
1
(
2
)
(
s
s
s
s
G
Znaleźć opis układu w przestrzeni fazowej (tj. przestrzeni stanu, gdzie kolejna współrzędna jest
pochodną poprzedniej).
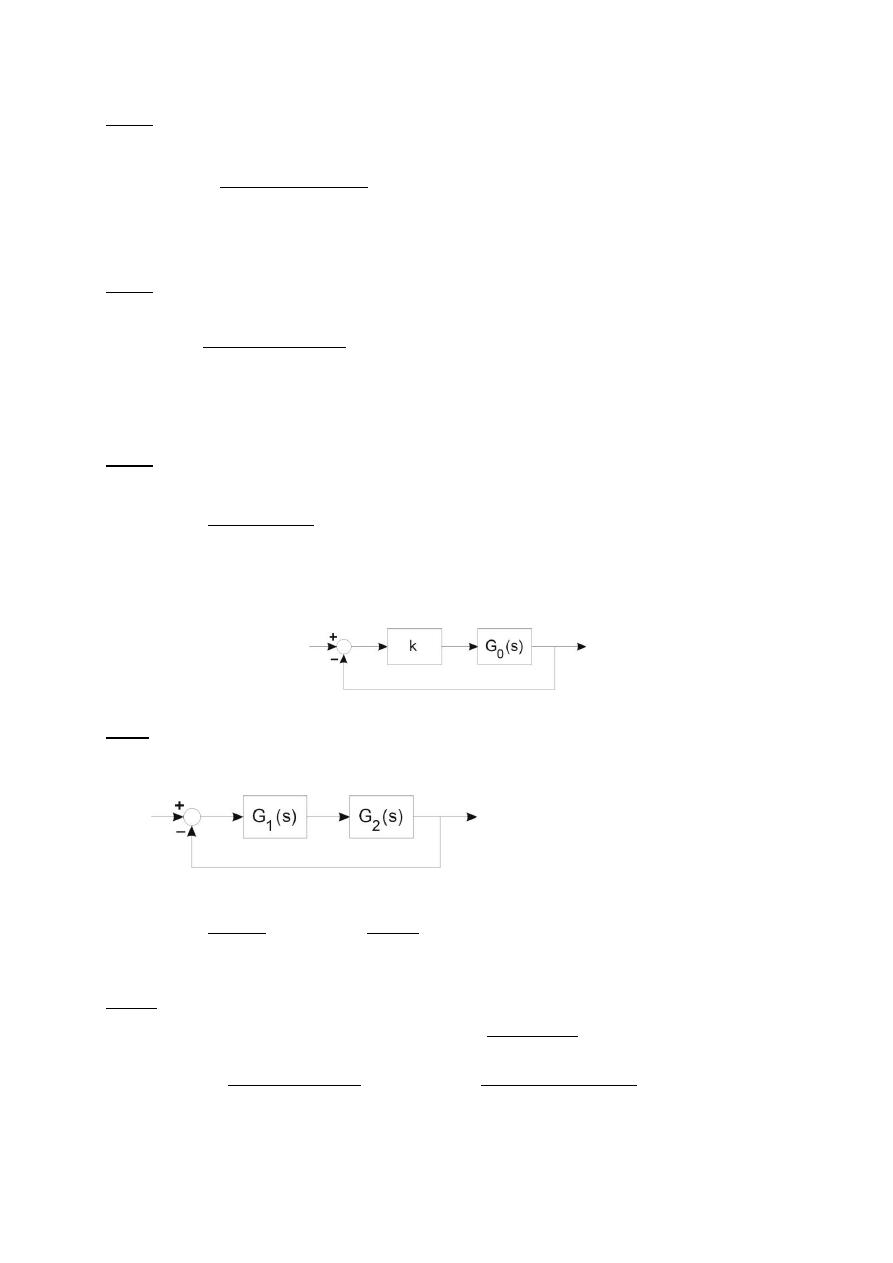
Zad. 6.
Wyznaczyć i narysować logarytmiczne charakterystyki modułu i fazy układu o transmitancji:
2
2
)
1
1
.
0
(
)
1
2
(
)
1
10
(
2
)
(
s
s
s
s
G
Na podstawie tych charakterystyk naszkicować charakterystykę amplitudowo-fazową układu.
Zad. 7.
Wyznaczyć i narysować logarytmiczne charakterystyki modułu i fazy układu o transmitancji:
)
1
01
.
0
(
)
1
(
)
1
05
.
0
(
)
1
2
.
0
(
)
(
s
s
s
s
s
s
G
Na podstawie logarytmicznych charakterystyk modułu i fazy naszkicować charakterystykę amplitudowo-
fazową tego układu.
Zad. 8.
Transmitancja operatorowa G
0
(s) liniowego układu dynamicznego ma postać:
)
1
(
)
1
(
1
)
(
0
Ts
s
s
s
G
Układ połączono szeregowo ze wzmacniaczem o wzmocnieniu k i zamknięto pętlą ujemnego
sprzężenia zwrotnego, jak na rysunku. Wyznaczyć i narysować obszar stabilności asymptotycznej
układu na płaszczyźnie (k, T). Do obliczeń należy zastosować kryterium Hurwitza.
Zad. 9.
Dla układu zamkniętego przedstawionego na poniższym rysunku wyznaczyć i narysować obszar stabilności
asymptotycznej na płaszczyźnie (k, T). Do obliczeń należy zastosować kryterium Hurwitza.
Należy ponadto założyć, że k > 0 i T > 0. Transmitancje G
1
(s) i G
2
(s) podane są poniżej:
2
2
1
)
1
(
1
)
(
;
)
1
(
)
(
s
s
G
s
T
k
s
G
Zad. 10.
Narysuj logarytmiczne charakterystyki częstotliwościowe (asymptotyczne charakterystyki Bodego) liniowych
układów dynamicznych o transmitancjach operatorowych:
2
2
1
)
1
02
.
0
(
)
1
10
(
)
1
(
100
)
(
)
;
)
1
5
(
)
01
.
0
(
01
.
0
)
(
)
s
s
s
s
s
G
b
s
s
s
s
G
a
oraz oszacuj zapasy stabilności każdego z tych układów.
Wyszukiwarka
Podobne podstrony:
Automatyka kol 2 2012 2013 przy Nieznany (2)
zagadnienia kol I 2012-2013, Studia, UR OŚ, semestr III, biochemia
zestaw lesny 15h 2012 2013 id 5 Nieznany
zagadnienia kol I 2012-2013, Studia, UR OŚ, semestr III, biochemia
kol zal sem2 EiT 2012 2013
kol zal sem2 AiR IBM 2012 2013
PKM-wały, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMiR, Aut
Cw Charakterystyki częstotliwościowe, Semestr III PK, Semestr Zimowy 2012-2013 (III), Automatyka, Au
plan lekcji 2012 2013 nowy id 3 Nieznany
kol zal pop sem2 EiT 2012 2013
2IA PS2 2012 2013 04 B id 32601 Nieznany (2)
badania preferencji 2012 2013 c Nieznany
M 2 GiK stacjonarne 2012 2013 i Nieznany
2012 2013 kolokwium nr 2 2012 2 Nieznany (2)
sprawko10, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMiR, Au
sprawko6, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMiR, Aut
więcej podobnych podstron