Semestr zimowy 2012/2013 Wydział Leśny 15h
Część 1
KINEMATYKA
Ruch jednostajny, prędkość wypadkowa, układ odniesienia

1.

Z łódki płynącej w górę rzeki ze stałą szybkością 3 m/s względem wody wypadło koło ratunkowe. Pasażer zauważył ten
fakt po upływie 5 min od chwili wypadnięcia koła i natychmiast zawrócił. Woda w rzece płynie z szybkością 1 m/s. Po
jakim czasie łódka dotrze do unoszonego z prądem koła? Rozwiązać zadanie dwoma sposobami, rozpatrując ruch łódki i
koła względem a) brzegu, b) rzeki. [5 min]

Prędkość względna

2.

Równolegle do siebie, w tym samym kierunku, poruszają się: pociąg o długości 200 [m] mający szybkość 10 [m/s] oraz
samochód jadący z prędkością 20 [m/s]. Po jakim czasie samochód wyprzedzi pociąg? Jaką drogę pokona samochód do
czasu, w którym wyprzedzi pociąg? [20 s, 400 m]

Prędkość średnia

3.

Łódź płynie rzeką z miejscowości A do B i z powrotem. Prędkość łodzi względem wody wynosi 5 [m/s], a prędkość
wody względem brzegów wynosi 4 [m/s]. Ile wynosi prędkość średnia ruchu łodzi (względem brzegu) na trasie ABA?
[1,8 m/s]

Ruch jednostajnie zmienny

4.

Ciało poruszające się po linii prostej ruchem jednostajnie przyśpieszonym bez prędkości początkowej przebywa w
pierwszej sekundzie drogę 5 [m]. Ile wynosi droga przebyta w trzydziestej sekundzie? [295 m]

5.

Samochód poruszający się 70 km/h zaczyna hamować. W ciągu 10 s jego prędkość spadła do 30 km/h. Jaką drogę w tym
czasie przejechał samochód. Ile czasu zajmie zatrzymanie się samochodu? [139 m, 17,6 s]

6.

Na rysunku przedstawiono wykres prędkości pojazdu w funkcji czasu. Jaką drogę przejechał pojazd w czasie pierwszych
7 sekund ruchu? [205 m]

0

10

20

30

40

50

60

70

80

0

1

2

3

4

5

6

7

8

czas [s]

p

r

ę

d

k

o

ś

ć

[

m

/s

]

DYNAMIKA
Środek masy

7.

Wyznacz położenie środka masy pręta o długości 2a i masie m zgiętego w połowie pod kątem 90°.

Druga zasada dynamiki Newtona

8.

Lokomotywa manewrowa pchnęła wagon o masie 40 ton, nadając mu prędkość początkową o wartości 5 [m/s]. Wagon,
poruszając się ruchem jednostajnie opóźnionym, zatrzymał się po upływie 20 [s]. Oblicz wartość siły hamującej wagon.
[10 000 N]

9.

Jeżeli pominiemy tarcie i masę bloczków, to ile wynosi przyspieszenie klocków i siła naciągu liny łączącej klocki? Masa
m=1 [kg]. [3,3 m/s

2

, 13,3 N]

m

2 m

Równia pochyła, tarcie

10.

Z równi pochyłej o kącie nachylenia 30 stopni zsuwa się skrzynia. Jaką wartość ma przyspieszenie skrzyni, jeśli
współczynnik tarcia kinetycznego wynosi 0,01? [4,9 m/s

2

]

Wypadkowy moment siły

11.

Ewa i Karol siedzą na huśtawce, która jest w równowadze. Odległości dzieci od miejsca podparcia podano na rysunku.
Jaka jest masa Karola, jeżeli masa Ewy wynosi 25 [kg]? [50 kg]

Praca, moc, energia mechaniczna

12.

Dźwig unosi w górę ciężar o masie 500 [kg] ze stałym przyśpieszeniem 1.2 [m/s

2

] na wysokość 10 [m]. Obliczyć pracę

jaką wykona silnik dźwigu. [56 kJ]

13.

Samochód, którego silnik pracuje z mocą 30 [kW], jedzie ze stałą prędkością 20 [m/s]. Ile wynosi siła napędowa
samochodu? [1500 N]

14.

Na ciało działa siła F(x), przy czym x jest przesunięciem ciała w kierunku działania siły. Praca wykonywana przez tę siłę
na drodze 20 [m] wynosi 300 [J]. Znajdź wartość siły F. [20 N]

Zasada zachowania energii

15.

Skoczek wzwyż o masie 90 [kg] pokonał poprzeczkę umieszczoną na wysokości 125 [cm]. Jaką prędkość musiał
uzyskać w wyniku odbicia się? [5 m/s]

16.

Po pionowym pręcie o wysokości 5 [m] zsuwa się pierścień o masie 500 g. Podczas zsuwania się pierścienia, działa na
niego siła tarcia, o średniej wartości 1,5 N. Ile wynosi prędkość w chwili zderzenia pierścienia z podłożem? [8,4 m/s]

Zasada zachowania pędu

17.

Pocisk o masie m

1

=20 [kg], lecący poziomo z prędkością v

1

=1000 [m/s], trafia w platformę z piaskiem o masie

m

2

=1 [tona] i grzęźnie w piasku. Z jaką prędkością v

2

zacznie poruszać się platforma? [19,6 m/s]

18.

Chłopiec o masie m

1

=50 [kg] zeskoczył ze stojącego wózka o masie m

2

=25 [kg] z prędkością skierowaną poziomo,

której wartość wynosi v

1

=1 [m/s]. Z jaką prędkością v

2

cofnął się wózek? [2 m/s]

19.

Dwaj ludzie o masie m

1

=60 [kg] i m

2

=50 [kg] biegnący naprzeciw siebie z prędkościami v

1

=10 [m/s] i v

2

=4 [m/s]

wskakują równocześnie na wózek o masie m

3

=60 [kg] stojący na ich drodze. Znajdź prędkość v

3

wózka z ludźmi,

pomijając siły tarcia wózka o ziemię. W którą stronę pojedzie wózek? [2,3 m/s]

Zadania domowe 1

1.

Sokół leci po linii prostej z prędkością 25 m/s, goniąc gołębia, który porusza się po tej samej prostej z prędkością 20 m/s.
Jeśli początkowa odległość między ptakami wynosiła 0,5 km, to po jakim czasie sokół dogoni gołębia? [100 s]

2.

Łódź płynie z prądem rzeki w czasie 3 [h], a pod prąd przepływa tę samą drogę w czasie 6 [h]. W jakim czasie tę samą
odległość, łódź przepłynie w dół rzeki z wyłączonym silnikiem? [12 h]

3.

Chłopiec postanowił zmierzyć prędkość i długość schodów ruchomych. Biegnąc z prędkością 2 schodów/sek w kierunku
przeciwnym do ruchu schodów chłopiec zauważył, że pozostaje na tej samej wysokości. Biegnąc zaś z prędkością 3
schodów/sek chłopiec zbiegł z nich w ciągu 10 sek. Oblicz prędkość i długość schodów. [2 schody/sek, 10 schodów]

4.

Pasażer pociągu poruszającego się z prędkością 10 [m/s] widzi w ciągu czasu 3 [s] wymijany pociąg o długości 75 [m]. Jaką
wartość ma prędkość wymijanego pociągu? [15 m/s]

5.

Samochód jedzie na północ z prędkością 72 km/h, a motocykl na wschód z prędkością 20 m/s. Jaki jest zwrot i prędkość
samochodu względem motocykla? [północny zachód, 28.3 m/s]

6.

Hydraulik idzie z prędkością 2,5 m/s trzymając w ręku rurę. Pada deszcz, a krople deszczu spadają pionowo z prędkością
10 m/s. Pod jakim kątem do pionu hydraulik musi trzymać rurę, aby deszcz nie zmoczył wnętrza rury? [14°]

7.

Pierwszą połowę drogi samochód przejechał z prędkością 80 [km/h], a drugą połowę drogi z prędkością 40 km/h. Jaka była
ś

rednia prędkość samochodu? [53.3 km/h]

8.

Ciało poruszające się ruchem jednostajnie przyspieszonym przebyło w pierwszej sekundzie ruchu drogę 5 m. Jaką drogę
przebyło to ciało w ciągu początkowych trzech sekund ruchu, a jaką w ciągu trzeciej sekundy ruchu? [45 m, 25 m]

9.

Obserwator stojący na peronie zauważył, że pierwszy wagon ruszającego przed nim pociągu minął go w czasie 3 s.
Zakładając, że ruch pociągu jest jednostajnie przyspieszony, oblicz ile sekund będzie go mijał cały pociąg składający się z 9
wagonów. [9s] Ile czasu będzie go mijał ostatni wagon? [0,5 s]

10.

Ciało spadające swobodnie ma w punkcie A prędkość 0.4 [m/s], a w punkcie B 2.5
[m/s]. Określić odległość AB. [0.3 m]

11.

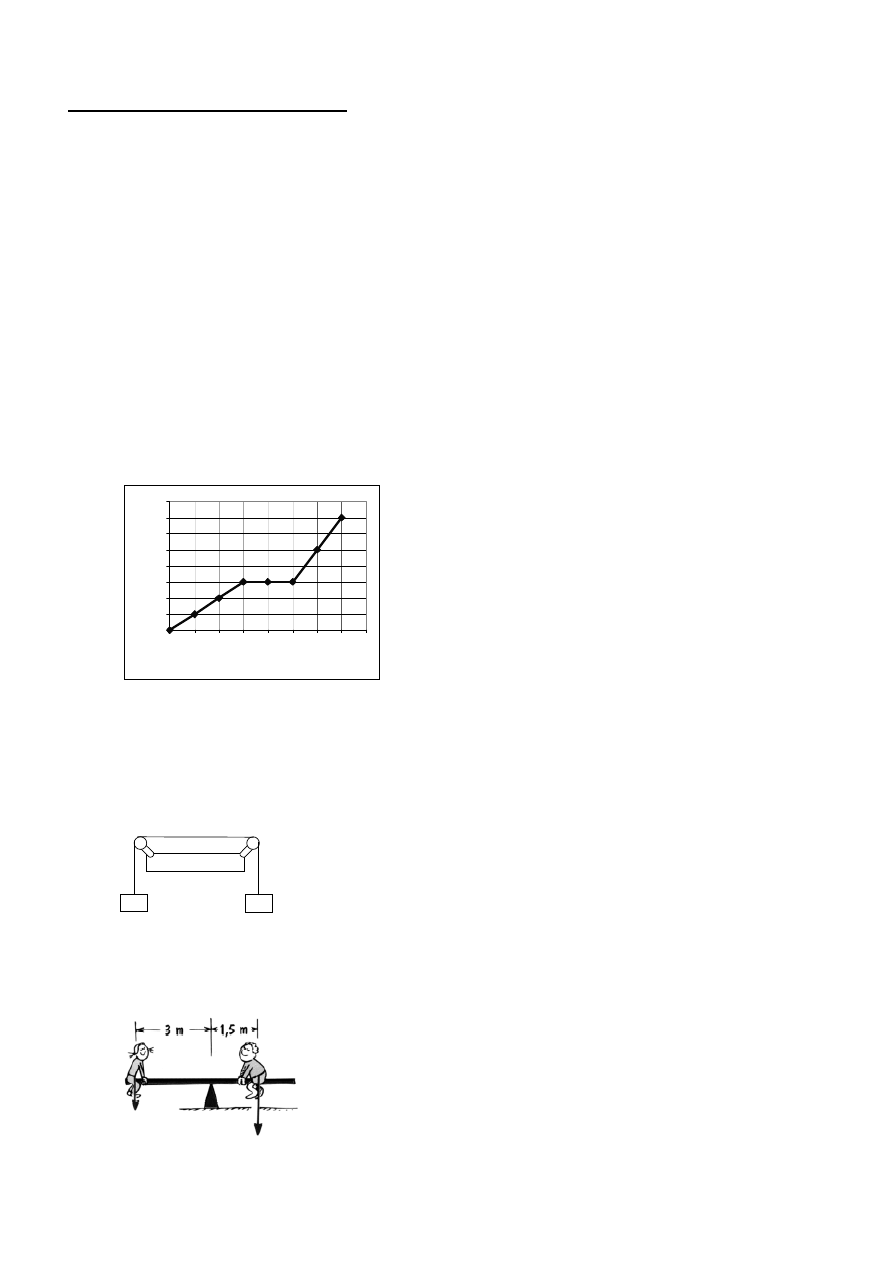
Określ prędkość początkową, przyspieszenie, drogę i prędkość średnią na podstawie
wykresu. [3 m/s, 1,25 m/s

2

, 22 m, 5,5 m/s]

12.

Czas wjeżdżania windy na wieżę telewizyjną o wysokości 322 [m] wynosi 60 [s]. Pierwszą część drogi winda przebywa ze
stałym przyspieszeniem do osiągnięcia prędkości 7 [m/s]. Drugą część drogi przebywa ruchem jednostajnym, a trzecią
ruchem jednostajnie opóźnionym. Obliczyć przyspieszenie z jakim winda rusza z miejsca przyjmując, że jest ono co do
wartości bezwzględnej równe opóźnieniu podczas hamowania. [0.5 m/s

2

]

13.

Pręt o długości 3a i masie m jest wygięty w kształcie litery U. Wyznaczyć środek masy.

14.

Jaką wartość ma siła, którą musimy działać na ciało o masie 5 [kg], aby podnieść je pionowo z przyspieszeniem 3 [m/s

2

]?

[65 N]

15.

Wózek o masie 0,8 kg ciągnięty przez sznurek, na którego końcu zawieszono obciążnik o masie 0,2 kg, porusza się po
powierzchni poziomej bez tarcia. Jakie jest przyspieszenie wózka? [2 m/s

2

]

16.

Ciału nadano prędkość początkową 2 m/s zwróconą ku górze gładkiej (tarcie pomijamy) równi pochyłej, nachylonej do
poziomu pod kątem 30°. Jak długo będzie trwał ruch pod górę? [0,4 s]

17.

Jasio ciągnie zabawkę o ciężarze P=20 N za sznurek skierowany pod kątem α=60° do podłogi. Siła napięcia sznurka wynosi
F=10 N, a współczynnik tarcia zabawki o podłogę jest równy 0,8. Czy zabawka ruszy z miejsca? [nie, Fcosα=5 N, T=9 N]

18.

Ciało swobodnie zsuwa się z wierzchołka równi pochyłej, której kąt nachylenia do poziomu wynosi 30 stopni. Wyznaczyć
czas ruchu ciała na równi, jeżeli wysokość równi pochyłej wynosi 1 [m], współczynnik tarcia 0.5. [2.5 s]

19.

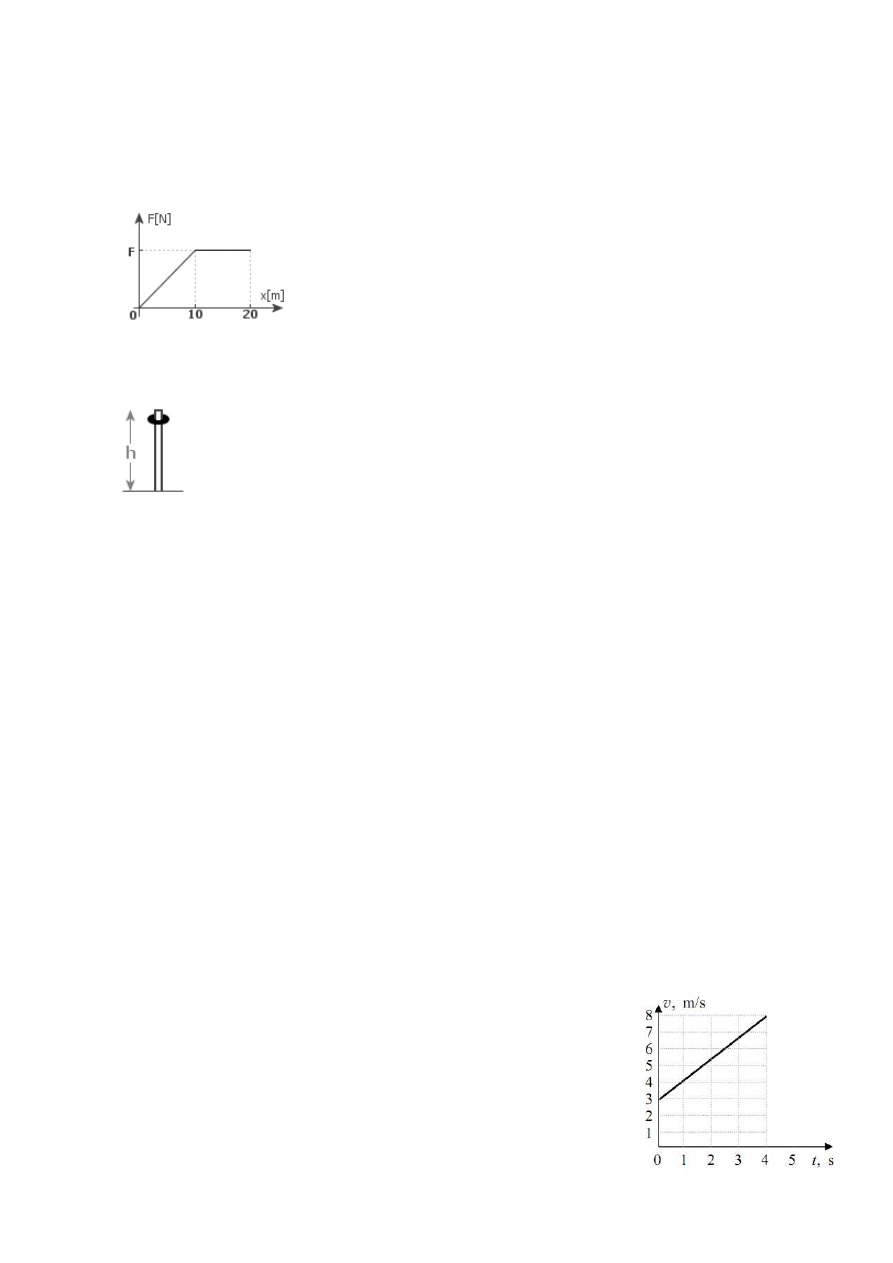
Uczniowie położyli na stole klocek, do którego doczepili siłomierz. Działając na klocek stałą siłą wprawili go w ruch i
mierzyli jego przyspieszenie a. Doświadczenie powtórzyli kilka razy przy różnych wartościach siły F wywieranej przez
siłomierz, a wyniki przedstawiono na poniższym wykresie. Ile wynosi siła tarcia? [0,9N]. Ile wynosi masa klocka? [1,6 kg]

a

a

a

20.

Drążek o długości 50 cm podparty jest na środku. Na drążku zawieszone są trzy ciężarki, jak na rysunku. Znajdź odległość
x, jeśli cały układ jest w równowadze. [5 cm]

21.

Oblicz, jaką pracę należy wykonać, aby ciało o masie 10 [kg] podnieść ze stałą prędkością na wysokość 10 [m]. Jaką pracę
należy wykonać, aby to samo ciało podnieść z przyspieszeniem 2 [m/s

2

]. [1 kJ, 1.2 kJ]

22.

Pociąg o masie 10 ton rusza ze stacji i po upływie 10 min. osiąga prędkość 36 km/h. Jaką pracę wykonały maszyny
napędowe pociągu, jeśli współczynnik tarcia wynosi 0,01? [3,6 MJ]

23.

Sportowiec o masie 80 kg podczas skoku wzwyż osiąga przy odbiciu prędkość 5 [m/s] w czasie 0.02 [s]. Ile wynosi moc
rozwijana w tym momencie przez sportowca? [50 kW]

24.

Ś

rednia moc tracona przez człowieka wynosi 110 W. Spalanie 1 g tłuszczu wyzwala energię równą 40000 J. Ile wynosi masa

tłuszczu traconego w ciągu doby przez człowieka prowadzącego głodówkę? [238 g]

25.

Wykres przedstawia zależność siły mięśni dwóch rowerzystów od przebytej drogi. Który z nich wykonał większą pracę?
[Adam 800J; Maciek 800J]

0

5

10

15

20

25

0

20

40

60

80

100

s [m ]

F

[

N

]

Adam

Maciek

26.

Gimnastyczka wyrzuciła pionowo w górę piłkę z prędkością o wartości 4 m/s. Piłka w momencie wyrzucania znajdowała się
na wysokości 1 m licząc od podłogi. Oblicz wartość prędkości, z jak pika uderzy o podłogę. Załóż, że na piłkę nie działa siła
oporu. [6 m/s]

27.

Aby wyładować beczki z gipsem z samochodu, położono pochylnię. Beczki staczały się z wysokości 100 cm i miały masę
100 kg każda. Oblicz, korzystając ze związku pomiędzy energią i pracą, zasięg toczenia się beczki po poziomej trawiastej
powierzchni. Przyjmij, że podczas toczenia się beczki po trawie działa na nią stała siła oporu o wartości 50 N. [20 m]

28.

Piłka spada z wysokości 5 m, a następnie odbija się od podłoża. W trakcie odbicia tracona jest jedna trzecia energii
kinetycznej piłki. Na jaką wysokość wzniesie się piłka po odbiciu? [3,33 m]

29.

Kulka wpadła do wody opadając z wysokości h=50 cm i zanurzyła się do głębokości H=20 cm. Zakładając, że ruch kulki w
wodzie jest jednostajnie opóźniony, obliczyć przyspieszenie kulki w wodzie. Opory pomijamy. [25 m/s

2

]

30.

Ciało porusza się pod wpływem stałej siły o kierunku i zwrocie zgodnym z przesunięciem. Oblicz stosunek pracy wykonanej
w pierwszej sekundzie ruchu do pracy wykonanej w drugiej sekundzie ruchu, jeżeli prędkość początkowa była równa zeru.
[1:3]

31.

Pocisk o masie 10 g lecący poziomo z prędkością 600 m/s wpada do pudła z piaskiem o masie 5 kg i grzęźnie w nim. Pudło
początkowo spoczywało na poziomym podłożu. Współczynnik tarcia pudła o podłoże wynosi 0,3. Oblicz odległość, na jaką
przemieści się pudło do chwili zatrzymania. [24 cm]

32.

Prędkość pocisku po przebiciu klocka o masie 0,5 kg leżącego na poziomym podłożu zmalała z 400 m/s do 200 m/s. Masa
pocisku wynosi 0,01 kg. Z jaką prędkością będzie poruszał się klocek? [4 m/s]. Ile wynosi strata energii kinetycznej układu
(układ = klocek + pocisk) podczas przebijania klocka przez pocisk? [596 J]

33.

Na gładkim lodzie stoi chłopiec o masie 50 [kg] trzymając w obu rękach dwa kamienie o łącznej masie 2 [kg]. Z jaką
prędkością zacznie poruszać się chłopiec, jeśli zamachnąwszy się rzuci on obydwa kamienie za siebie z prędkością 5 [m/s]
względem ziemi? [0,2 m/s]

15 N

10 N

50 cm

x

25 N

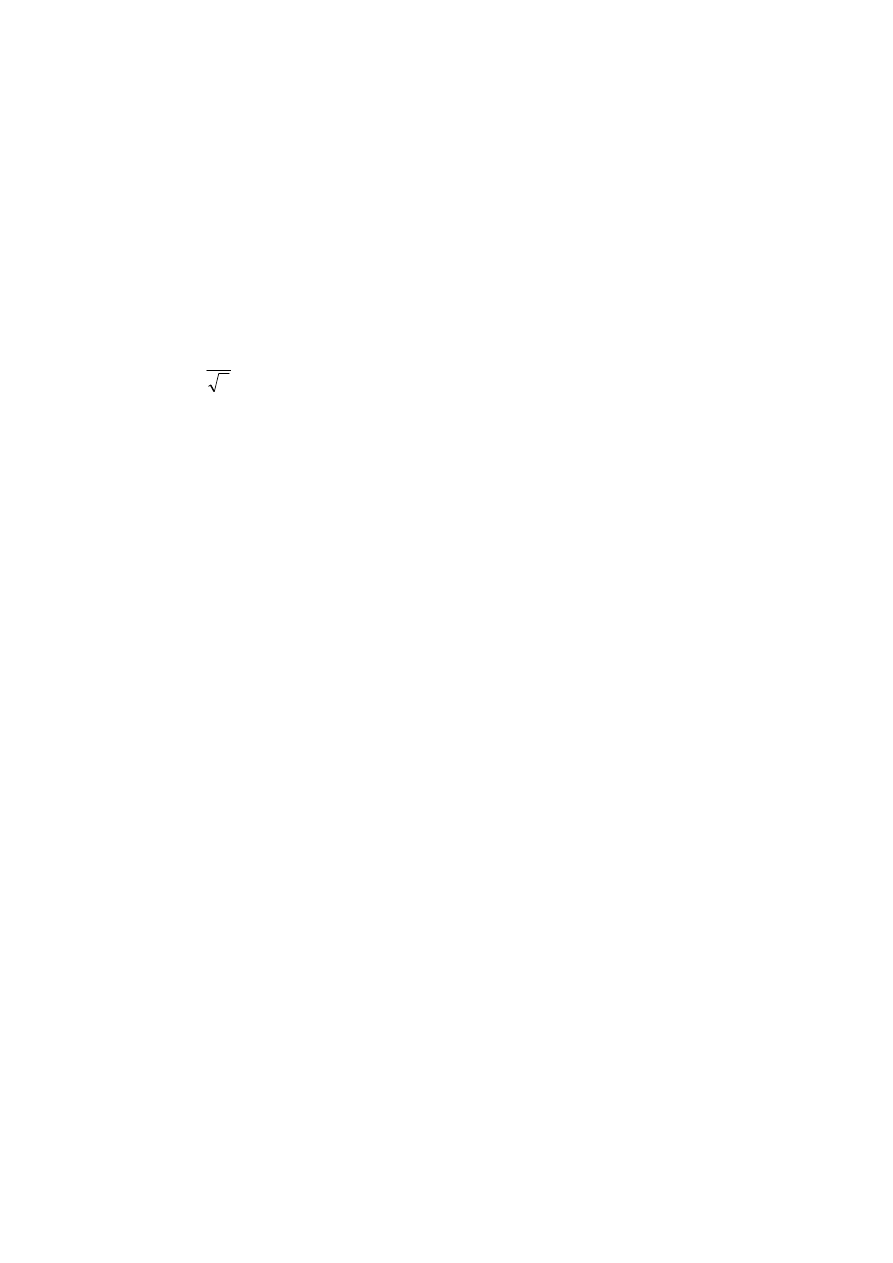
34.

Cztery jednakowe ciała o równych masach po 20 [g] każde leżą na jednej prostej w pewnych odległościach od siebie. W
pierwsze ciało uderza takie samo ciało, które porusza się z prędkością 10 [m/s] wzdłuż prostej, na której są umieszczone
ciała. Traktując zderzenia jako doskonale niesprężyste, znaleźć energię kinetyczną układu ciał po zakończeniu zderzeń.
[0.2 J]

Część 2
DRGANIA
Wahadło matematyczne, układ nieinercjaln

1.

Wahadło zegara ma okres drgań 1 s. Zegar umieszczono w poruszającej się do góry windzie i stwierdzono, że w czasie
15 s wahadło wykonało 10 pełnych wahnięć. Czy winda przyspieszała czy hamowała? Jaka była bezwzględna wartość
przyspieszenia? [winda hamowała z opóźnieniem 5,4 m/s

2

]

Wahadło sprężynowe

2.

Ciało o masie 1 [kg] rozciąga sprężynę o 16 [cm] w porównaniu z jej długością przed rozciągnięciem. Oblicz
współczynnik sprężystości sprężyny oraz okres drgań ciała na sprężynie. [62.5 N/m, 0.8 s]

Energia potencjalna sprężystości

3.

Kula wykonuje drgania harmoniczne. Oblicz wychylenie, przy którym energia kinetyczna kuli jest równa energii

potencjalnej. [

2

A

]

FALE

4.

Statek płynący po jeziorze wywołał falę, która doszła do brzegu po jednej minucie. Odległość między sąsiednimi
grzbietami fali jest równa 1,5 m, a czas pomiędzy dwoma kolejnymi uderzeniami fali o brzeg jest równy 2 s. Jaka jest
odległość przepływającego statku od brzegu? [45 m]

5.

Nietoperz wysyła falę dźwiękową o częstotliwości 70 [kHz]. Wiedząc, że fala akustyczna skutecznie odbija się od
obiektów mającej co najmniej połowę długości fali, oblicz jaki najmniejszy obiekt może zlokalizować nietoperz.
Prędkość dźwięku w powietrzu wynosi 330 [m/s]. [2,3 mm]

6.

Fala akustyczna przechodzi z powietrza do wody. Prędkość tej fali w powietrzu wynosi 330 [m/s], a w wodzie 1485
[m/s]. Długość fali w powietrzu jest równa 2 [m]. Oblicz długość fali w wodzie. [9 m]

HYDROSTATYKA I HYDRODYNAMIKA
Siła wyporu

7.

Kula o masie 10 g pływa w cieczy, zanurzona do 1/3 swojej objętości. Jaką siłą zwróconą pionowo w dół należy
podziałać na kulę, aby ją całkowicie zanurzyć? [0,2 N]

8.

Wyznacz gęstość jednorodnego ciała, którego ciężar w powietrzu wynosi 2.8 [N], a w wodzie 1.8 [N]. Pomiń siłę
wyporu powietrza. [2800 kg/m

3

]

Ciśnienie hydrostatyczne

9.

Do rurki w kształcie litery U nalano rtęci, a na jej powierzchnię w jednym ramieniu wlano oliwę o gęstości 920 kg/m

3

, a

w drugim ramieniu naftę o gęstości 800 kg/m

3

. Wysokość słupków oliwy i nafty wynosiła odpowiednio 48 cm i 20 cm.

Oblicz różnicę poziomów rtęci w obu ramionach rurki wiedząc, że gęstość rtęci wynosi 13600 kg/m

3

. [ 2 cm]

Prawo Pascala

10.

Podnośnik hydrauliczny jest wyposażony w dwa cylindry o średnicach 50 [cm] i 100 [cm]. Jaką siłą należy nacisnąć
mniejszy tłok, aby większy mógł podnieść samochód o masie 1000 [kg]? [2500 N]

Przepływ cieczy

11.

Woda przepływa przez rurę kanalizacyjną o średnicy 10 [cm] z prędkością 0.1 [m/s]. W pewnym miejscu rura rozszerza
się i jej średnica wynosi 20 [cm]. Wyznacz różnicę ciśnienia wody w obu odcinkach rury. [4,8 Pa]

TERMODYNAMIKA
Przemiany gazowe

12.

Stalowy zbiornik zawiera azot pod ciśnieniem 1200 [kPa]. Temperatura gazu wynosi 27

o

C. Zbiornik zabezpieczony jest

zaworem bezpieczeństwa, który otwiera się gdy ciśnienie gazu przekroczy 1500 [kPa]. Zbiornik wystawiono na działanie
promieni słonecznych, w wyniku czego temperatura gazu wzrosła do 77

o

C. Podaj, czy w opisanej sytuacji nastąpi

otwarcie zaworu. [nie, 1400 kPa]

Przepływ ciepła

13.

Ile energii musimy dostarczyć do 1 kg lodu o temperaturze – 10

°

C by otrzymać 1 [kg] wrzątku? Ciepło właściwe lodu

2.1 [kJ/(kg K)], ciepło właściwe wody 4.2 [kJ/(kgK)], ciepło topnienia lodu 0.3 [MJ/kg]. [741 kJ]

14.

Kalorymetr mosiężny o masie 200 [g] zawiera 400 [g] aniliny o temperaturze 10 °C. Do kalorymetru dolano 400 [g]
aniliny o temperaturze 31 °C. Wyznacz ciepło właściwe aniliny, jeżeli po wymieszaniu temperatura ustaliła się i wynosi
20 °C. Ciepło właściwe mosiądzu wynosi 400 [J/kgK]. [2000 J/kgK]

Sprawność silnika

15.

Sprawność silnika cieplnego wynosi 20%. W ciągu 1 [h] silnik oddaje chłodnicy 20 [kJ] energii. Ile energii cieplnej z
grzejnika pobiera w tym samym czasie ów silnik? [25 kJ]

ELEKTRYCZNOŚĆ
Natężenie prądu, prawo Ohma

16.

Jaki ładunek przepływa przez przewodnik o oporze 4 [

Ω

] dołączony do źródła napięcia 12 [V], w czasie 1 minuty?

[180 C]

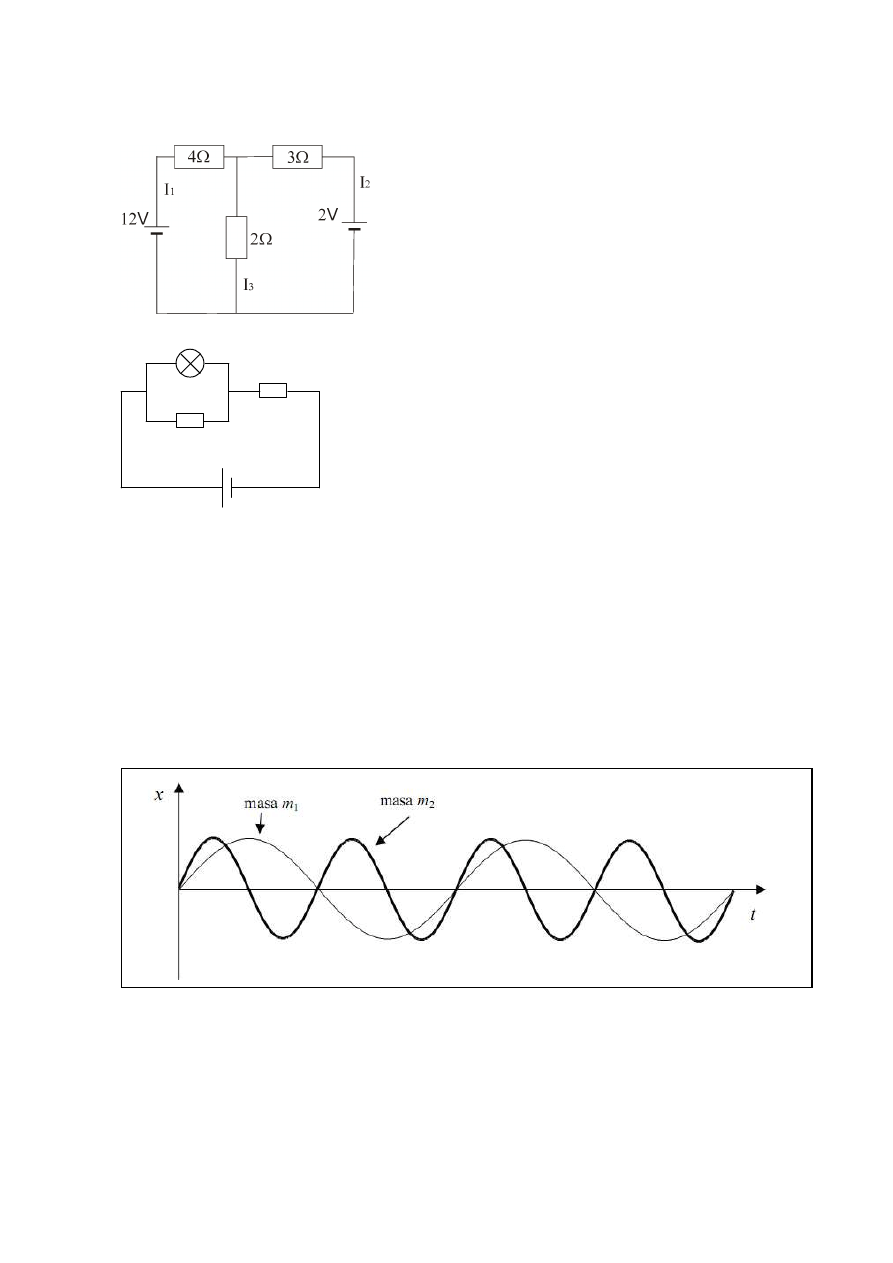
Obwody elektryczne

17.

Obliczyć natężenia prądów płynących w gałęziach obwodu, którego schemat przedstawiono na rysunku. [I

1

– 2,15 A, I

2

–

-0,46 A, I

3

– 1,69 A]

18.

W przedstawionym obwodzie bateria wytwarza napięcie 9 V. śarówka ma opór 6

Ω

. Jaki prąd będzie płynął przez

ż

arówkę? Jaką moc wydzieli się na żarówce? [0.8 A, 3.8 W]

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

R1=4

R2=2

Praca prądu

19.

Jakiej wartości nie może przekroczyć praca wykonana w ciągu 1 [h] przez urządzenie z bezpiecznikiem 10 [A],
podłączone do napięcia 200 [V]? [7,2 MJ]

Zadania domowe 2

1.

Wahadło wykonuje na Ziemi wahania o okresie 1 [s]. Jaki będzie okres drgań tego wahadła na Neptunie
(g

N

= 14 [m/s

2

])? [0,84 s]

2.

Na dwóch różnych sprężynach zawieszono różne masy. Na pierwszej sprężynie zawieszono masę 100 [g], a na drugiej
sprężynie masę 300 [g]. Jaki warunek muszą spełnić współczynniki sprężystości, aby wychylenia sprężyn były jednakowe?
[1:3]

3.

Uczeń chce zbudować dwa wahadła: matematyczne i sprężynowe, o takim samym okresie drgań. Dysponuje lekką sprężyną
o współczynniku sprężystości równym 7 N/m, dwoma małymi ciężarkami o masie 500 g każdy oraz nicią o długości 0,5 m
(którą można skrócić w razie potrzeby). Czy uczniowi uda się zrealizować ten pomysł? [nie, minimalny okres drgań wahadła
sprężynowego 1,68 s, maksymalny okres drgań wahadła matematycznego 1,4 s]

4.

Wykres przedstawia zależność wychylenia od czasu dla dwóch mas m

1

lub m

2

zawieszonych kolejno na tej samej sprężynie.

Ile wynosi okres drgań ciężarka m

1

i m

2

? [0.5 s, 0.25 s]. Ile wynosi stosunek mas m

1

:m

2

? [4:1].

5.

Klocek ma masę 100 [g] i jest zawieszony na sprężynie o współczynniku sprężystości 10 [N/m]. Oblicz wartość
przyspieszenia drgającego klocka w chwili, gdy jest wychylony o 5 [cm]. [5 m/s

2

]

6.

Obliczyć amplitudę drgań harmonicznych punktu materialnego, jeżeli jego całkowita energia mechaniczna 0,04 [J], a
działająca nań siła przy wychyleniu do połowy amplitudy wynosi 2 [N]. [0.02 m]

7.

Jaka jest szybkość rozchodzenia się fal na wodzie, jeżeli okres drgań łódki wynosi 4 [s], a odległość pomiędzy sąsiednimi
grzbietami fal wynosi 8 [m]? [2 m/s]

8.

Telefon komórkowy działa na częstotliwości 1200 [MHz]. Jaka jest długość fali odbieranych i wysyłanych przez
„komórkę”? [0.25 m]

9.

Prędkość rozchodzenia się ultradźwięków w stali wynosi 5100 m/s, a w wodzie 1490 m/s. Jaka jest długość fali w wodzie,
jeśli w stali wynosi 25 cm? [7,3 cm]

[s]

1

0,5

10.

Łódź podwodna o masie 523 [ton] ma objętość 602 [m

3

]. Oblicz, ile wody morskiej muszą wchłonąć zbiorniki łodzi

podwodnej, aby została całkowicie zanurzona. [79 m

3

]

11.

W wodzie o gęstości 1 [kg/dm

3

] pływa sześcian drewniany o gęstości 0.6 [g/cm

3

]. Krawędź sześcianu wynosi 0.1 [m].

Oblicz wysokość zanurzonej części sześcianu. [6 cm]

12.

Wyznacz siłę nośną balonu-sondy napełnionego helem, jeśli pojemność powłoki wynosi 200 m

3

, a jej ciężar łącznie z

instrumentami pomiarowymi wynosi 1900 N. Gęstość powietrza wynosi 1,29 kg/m

3

, gęstość helu 0,178 kg/m

3

. [324 N]

13.

Przedmiot jednorodny waży w powietrzu 9.81 [N]. Przedmiot ten zanurzony całkowicie w wodzie destylowanej waży
6.54 [N]. Ile wynosi objętość tego przedmiotu? [3.3·10

-4

m

3

]

14.

Dwa klocki sześcienne wykonane z metali o gęstościach 3600 [kg/m

3

] i 2300 [kg/m

3

] zanurzone w wodzie ważą tyle samo.

Jaki jest stosunek ich objętości? [1:2]

15.

Do rurki w kształcie litery U nalano rtęci (d

r

=13600 [kg/m

3

]), a następnie do jednego ramienia dolano wody, a do drugiego

nafty (d

n

=800 [kg/m

3

]). Powierzchnie swobodne wody i nafty znajdują się na jednakowym poziomie. Słupek wody ma

długość 64 [cm]. Obliczyć różnicę poziomów rtęci. [1 cm]

16.

W prasie hydraulicznej lewy tłok ma średnicę 10 razy mniejszą niż prawy. Jaką siłę należy przyłożyć do lewego tłoka, by
zrównoważyć ciężar o masie 100 [kg] położony na prawy tłok? [10 N]

17.

Oblicz, z jaką prędkością wypływa woda ze strzykawki, której pole powierzchni przekroju otworu wynosi 0.5 [mm

2

], jeżeli

tłok o polu powierzchni przekroju 1 [cm

2

] przemieszcza się z prędkością 2 [cm/s]. [4 m/s]

18.

W poziomej rurze płynie woda. W miejscu, gdzie średnica rury wynosi 4 cm, szybkość wody wynosi 1 m/s, a ciśnienie
150 kPa. Jakie ciśnienie panuje w miejscu, w jakim średnica rury zwęża się do 2 cm? [148,5 kPa]

19.

Temperaturę pewnego gazu podwyższono z 25°C do 100°C. Jego ciśnienie nie zmieniło się. Jak zmieniła się objętość tego
gazu? [wzrosła o 25%]

20.

W objętości 0,4 [m

3

] znajduje się masa 12 [g] gazu, którego temperatura wynosi 177[°C]. W jakiej temperaturze gęstość

tego gazu jest równa 0,06 [kg/m

3

], jeżeli ciśnienie pozostaje stałe? [-48

°

C]

21.

Z butli o pojemności 0,01 m

3

ulatnia się gaz o masie molowej 32 g/mol, W temperaturze 280 K manometr wskazuje

ciśnienie 5·10

6

Pa. Po pewnym czasie w temperaturze 290 K manometr wskazał to samo ciśnienie. Obliczyć masę gazu,

który się ulotnił. [23,7 g]

22.

Objętość pęcherzyka powietrza w miarę wypływania z dna jeziora na powierzchnię powiększa się trzy razy. Obliczyć
głębokość jeziora. Ciśnienie atmosferyczne 100 kPa. Temperatura wody jest wszędzie jednakowa. [20 m]

23.

Do ścianek cylindra wypełnionego gazem doskonałym przylega szczelnie ruchomy tłok, który dzieli objętość cylindra w
stosunku 1:2. Ciśnienie gazu i temperatura są początkowo w obu częściach cylindra jednakowe. Gaz zawarty w pierwszej
części cylindra ogrzewamy do temperatury 127 [

°

C], a gaz w drugiej części cylindra oziębiamy do -73 [

°

C]. Jakie położenie

zajmie tłok po wyrównaniu ciśnień w obu częściach cylindra? [tłok będzie po środku cylindra, czyli podzieli cylinder w
stosunku 1:1]

24.

Kawałek ołowiu o masie 1 [kg] po dostarczeniu mu ciepła 54.5·10

3

[J] osiągnął temperaturę topnienia i połowa ołowiu

uległa stopieniu. Jaka była temperatura początkowa ołowiu? Ciepło topnienia ołowiu 2.4·10

4

[J/kg], ciepło właściwe ołowiu

130 [J/kg K], temperatura topnienia ołowiu 327 [

°

C]. [0

°

C]

25.

Do naczynia zawierającego 3 [kg] wody o temperaturze 17 [ºC] włożono 0.5 [kg] cynku ogrzanego do temperatury 100 [ºC].
Temperatura wody z cynkiem wzrosła do 18.3 [ºC]. Jakie jest ciepło właściwe cynku? [400 J/kgK]

26.

Energia elektryczna jest przekazywana z elektrowni do odbiorcy w ten sposób, że najpierw urządzenie A podwyższa
napięcie otrzymywane z generatorów elektrowni, a następnie prąd jest przesyłany do odbiorcy, gdzie urządzenie B obniża
napięcie do wymaganej wartości. Sprawność każdego z urządzeń A i B wynosi 90%, a w linii przesyłowej traci się 5% tej
energii, którą oddaje urządzenie A. Oblicz sprawność przekazywania energii od elektrowni do odbiorcy. Możesz przyjąć, że
moc wytwarzana w generatorach elektrowni ma pewną zadaną wartość, np. 1000 MW. [77%]

27.

Silnik cieplny wykonał pracę podnosząc ciało o masie 20 ton na wysokość 50 m. Równocześnie oddał do chłodnicy tyle
ciepła, że stopiło się 1000 kg lodu o temperaturze 0°C. Oblicz sprawność silnika. Ciepło topnienia lodu 335000 J/kgK. [3%]

28.

Bateria wyczerpie się po godzinie, jeżeli będzie pobierany z niej prąd stały o natężeniu 8.1 [A]. Oblicz, jaki ładunek wtedy
przepłynie. Wynik podaj w kulombach. Przez żarówkę latarki zasilanej tą baterią płynie prąd stały o natężeniu 0.3 [A]. Po
ilu godzinach używania tej latarki wyczerpie się bateria? [29160 C; 27 h]

29.

Jakie jest natężenie prądu płynącego przez opornik R? Siła elektromotoryczna każdego ogniwa wynosi 3V. Opór
wewnętrzny ogniw wynosi 0.Opornik R ma opór 9

Ω

. [0,33 A]

R

30.

Ogniwa A i B połączono szeregowo tak, że biegun dodatni A był połączony a) z biegunem ujemnym B, b) z biegunem
dodatnim B. Amperomierz włączony do obwodu wskazywał natężenie I

a

=2,4 A, I

b

=0,6 A. Kierunek prądu był w obu

przypadkach taki sam. Opór całkowity obwodu jest w obu przypadkach taki sam. Oblicz stosunek sił elektromotorycznych

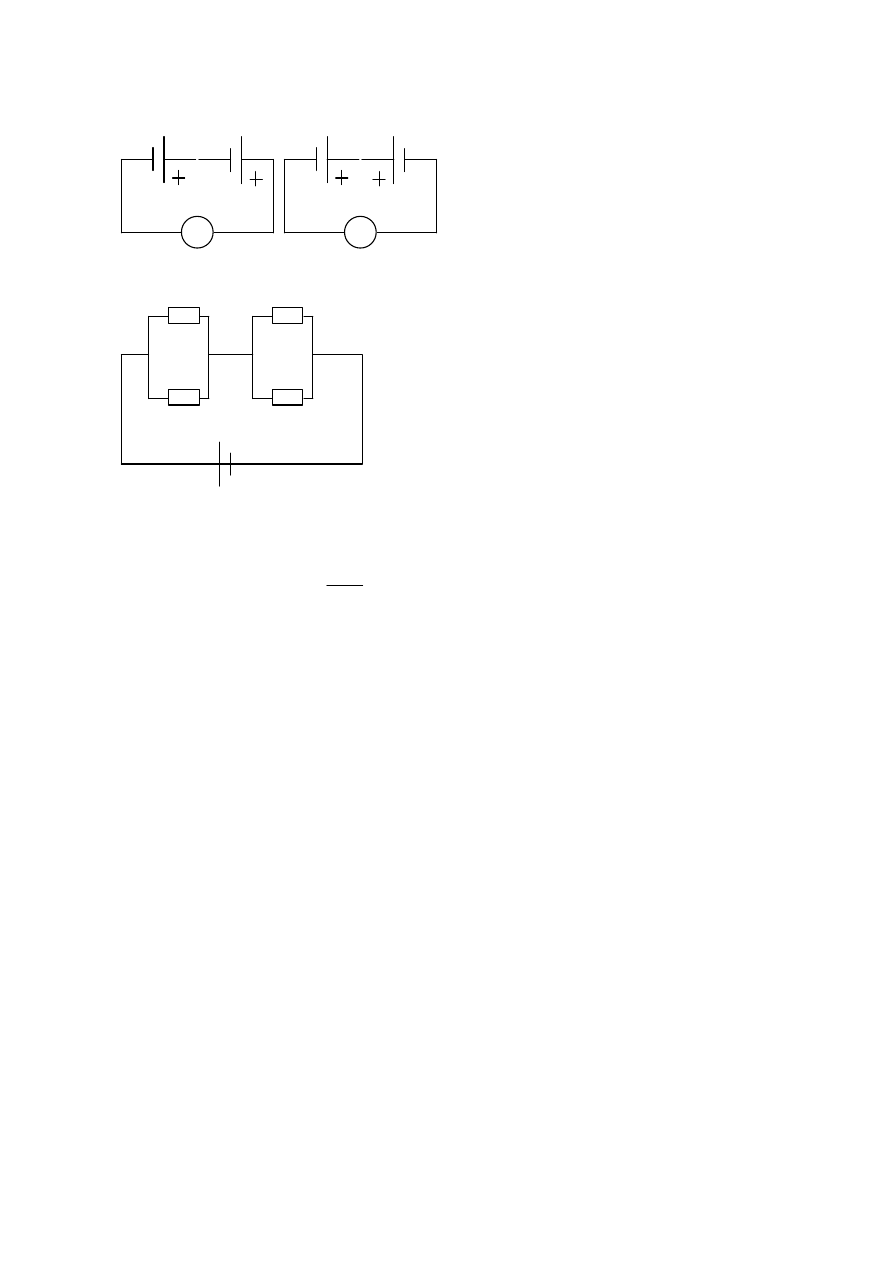
ogniw A i B ε

A

/ε

B

. [5:3]

A

A

B

A

A

B

31.

Ile wynosi prąd przepływający przez opornik 1

Ω

? [1,7 A]

1

2

6 V

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

3

4

32.

Kilowatogodzina jest pobierana przez odbiornik 20-omowy w czasie 30 minut. Jakie jest natężenie prądu? [10 A]

33.

Aby zagotować (doprowadzić do temperatury 100 [

°

C] 2 [kg] wody o temperaturze początkowej 20 [

°

C] użyto grzałki

elektrycznej o efektywnym oporze pracy 35 [Ω]. Po 5 minutach zasilania grzałki ze źródła prądu przemiennego woda
zaczęła wrzeć. Oblicz wartość skuteczną natężenia prądu płynącego przez grzałkę. Sprawność procesu podgrzewania wynosi

75 %. Ciepło właściwe wody 4200

K

kg

J

⋅

. [9.2 A]

34.

Jak się zmieni czas potrzebny do zagotowania wody, gdy dwie grzałki o jednakowej mocy połączymy szeregowo i
włączymy do sieci? [Czas będzie 2 razy dłuższy niż w przypadku zastosowania tylko jednej grzałki]

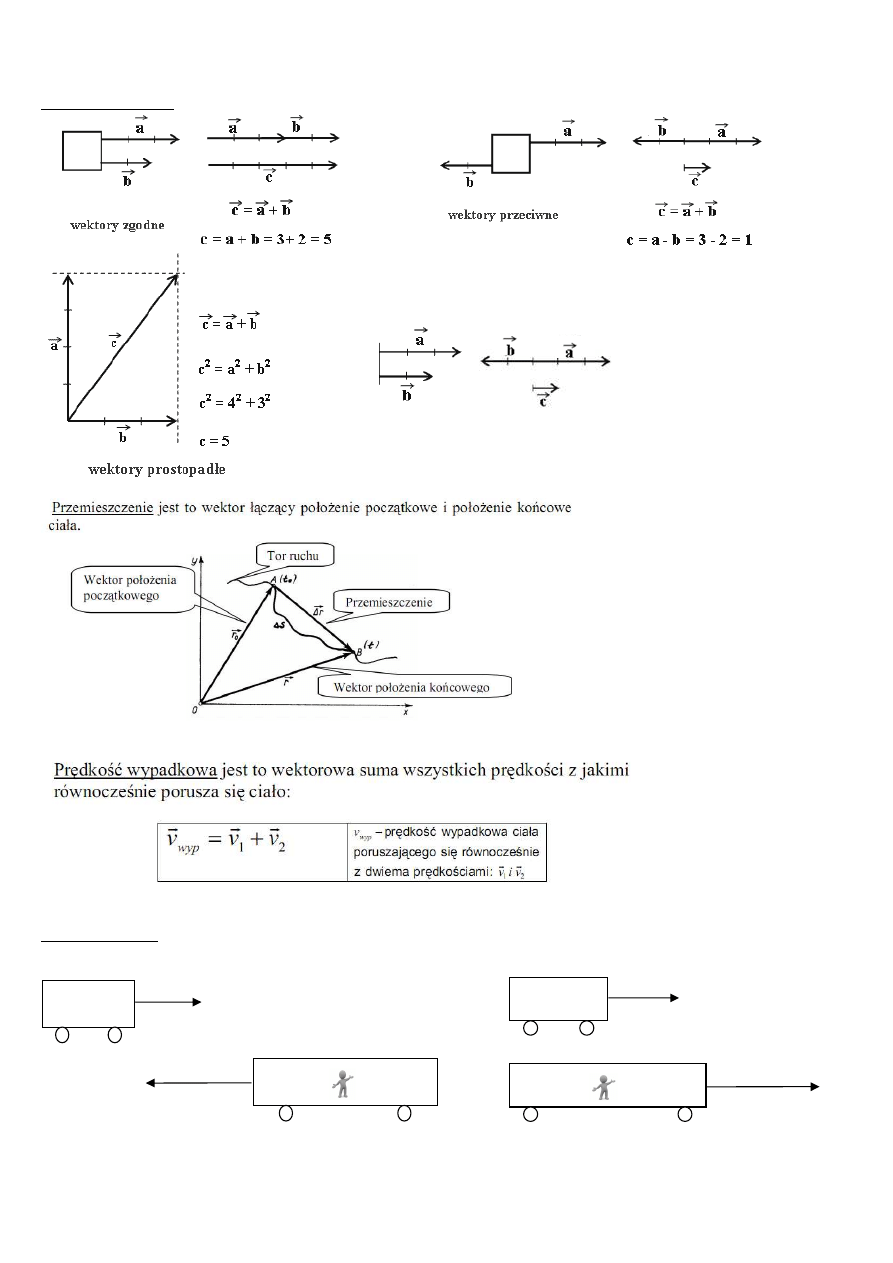
Dodawanie wektorów:

0

r

r

r

r

r

r

−

=

∆

Prędkość względna

AB

v

r

- prędkość ciała A względem ciała B

A

v

r

B

v

r

A

v

r

B

v

r

B

A

AB

B

A

AB

v

v

v

v

v

v

+

=

−

=

r

r

r

B

A

AB

B

A

AB

v

v

v

v

v

v

−

=

−

=

r

r

r

Wektory odejmuje się dodając wektor o przeciwnym zwrocie,
np.:

b

a

c

b

a

c

−

=

−

=

r

r

r

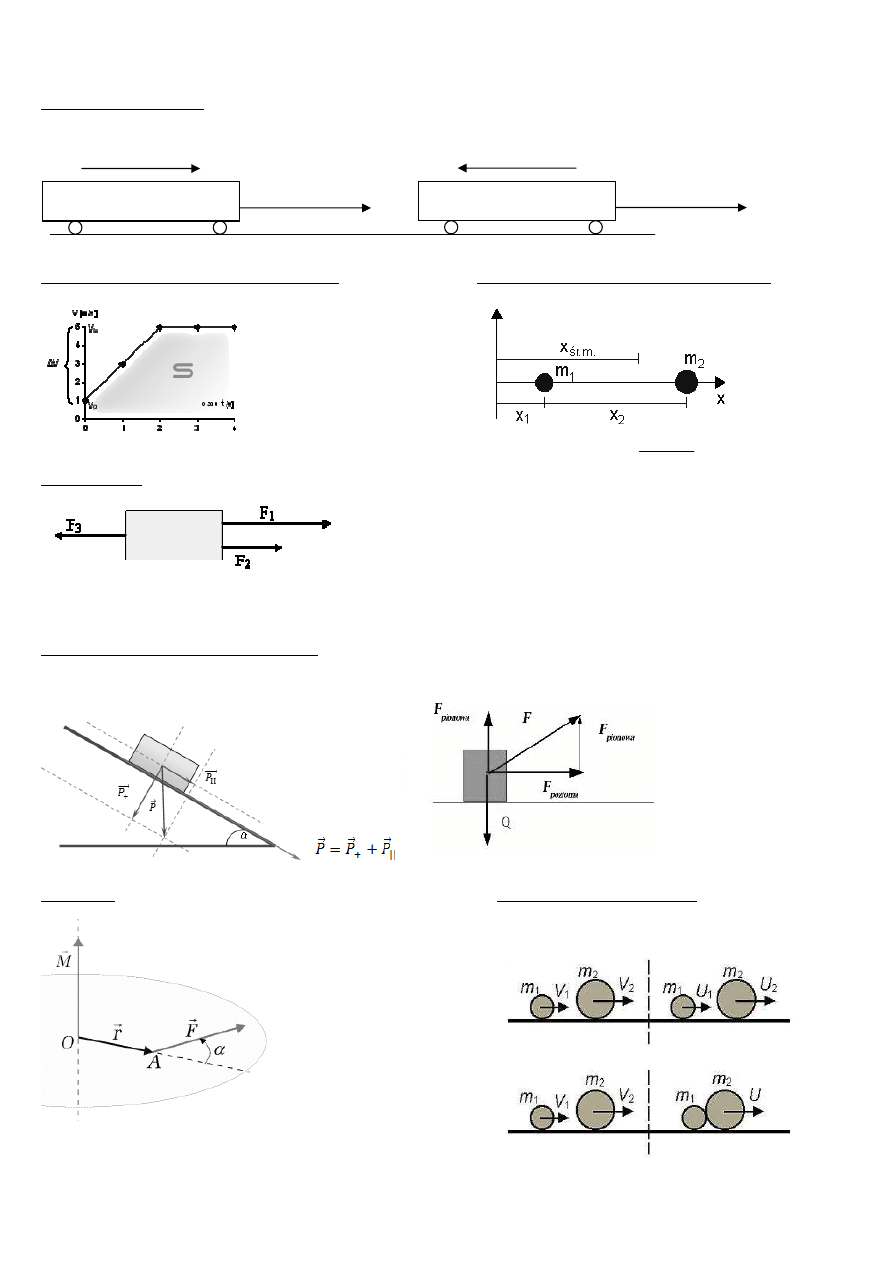
Przyspieszenie i opóźnienie

Graficzne wyznaczanie drogi na wykresie v=f(t)

Położenie środka masy w układzie współrzędnych

S – pole wielokąta

Siła wypadkowa F

w

– suma wektorowa wszystkich działających na ciało sił.

3

2

1

3

2

1

F

F

F

F

F

F

F

F

w

w

−

+

=

+

+

=

r

r

r

r

Rozkładanie wektora siły na wektory składowe

pozioma

pionowa

F

F

F

r

r

r

+

=

Moment siły

Zderzenia sprężyste i niesprężyste

α

sin

⋅

⋅

=

r

F

M

r

r

r

a

r

a

r

v

r

przyspieszenie

v

r

opóźnienie

Zderzenie sprężyste

Zderzenie niesprężyste

)

(

1

2

2

1

1

2

1

.

.

x

m

x

m

m

m

x

m

ś

r

+

+

=

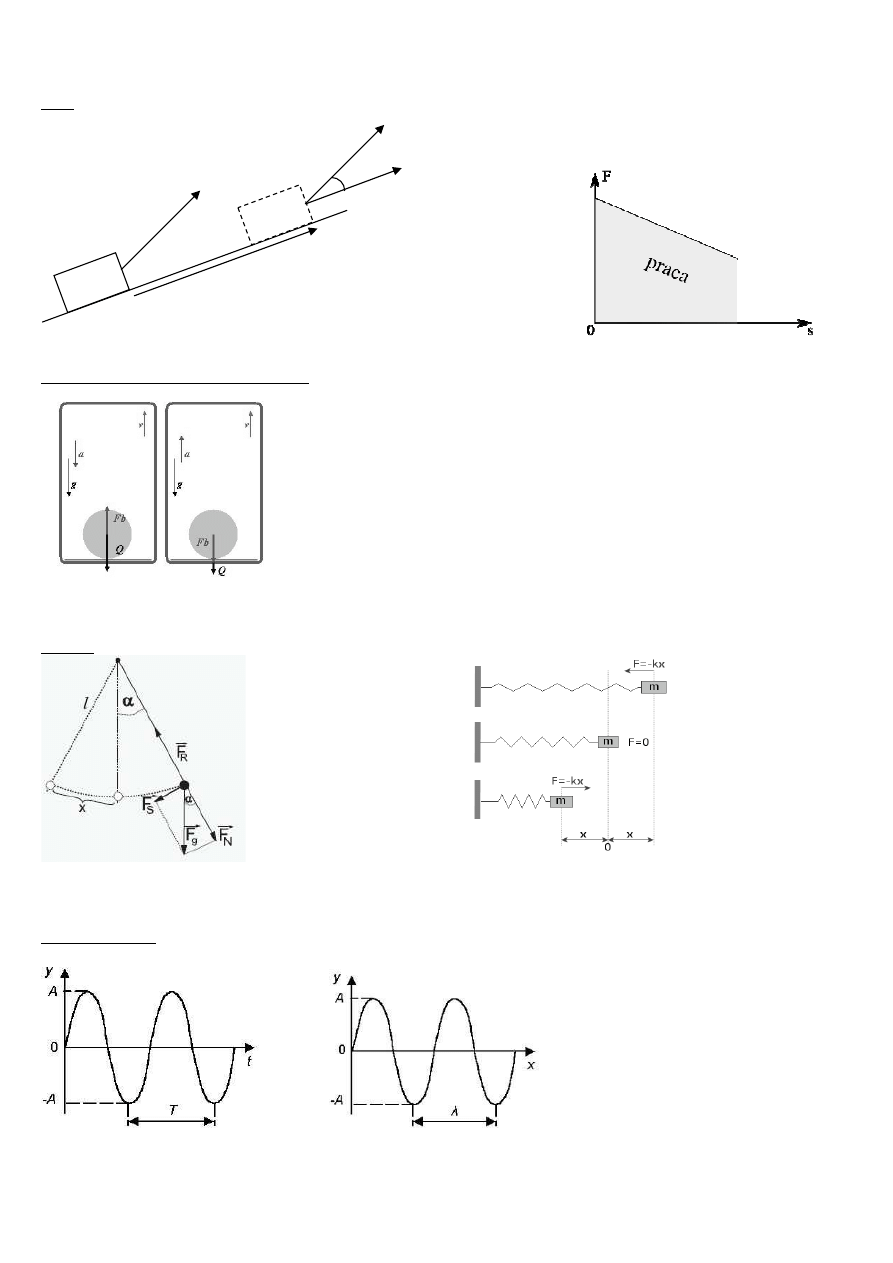
Praca

Siła bezwładności w układzie nieinercjalnym (winda hamująca i winda przyspieszająca)

g- przyspieszenie ziemskie, a- przyspieszenie windy, v – prędkość windy, F

b

- siła bezwładności, Q- ciężar

Wahadło

siła F

S

(część ciężaru F

g

) wywołuje ruch ciężarka

siła F (siła sprężystości) wywołuje ruch ciężarka

Okres i długość fali

s

r

F

r

α

cos

F

F

s

=

α

s

F

W

s

F

W

s

F

W

s

⋅

=

⋅

=

⋅

=

α

cos

r

r

F

r

matematyczne

sprężynowe

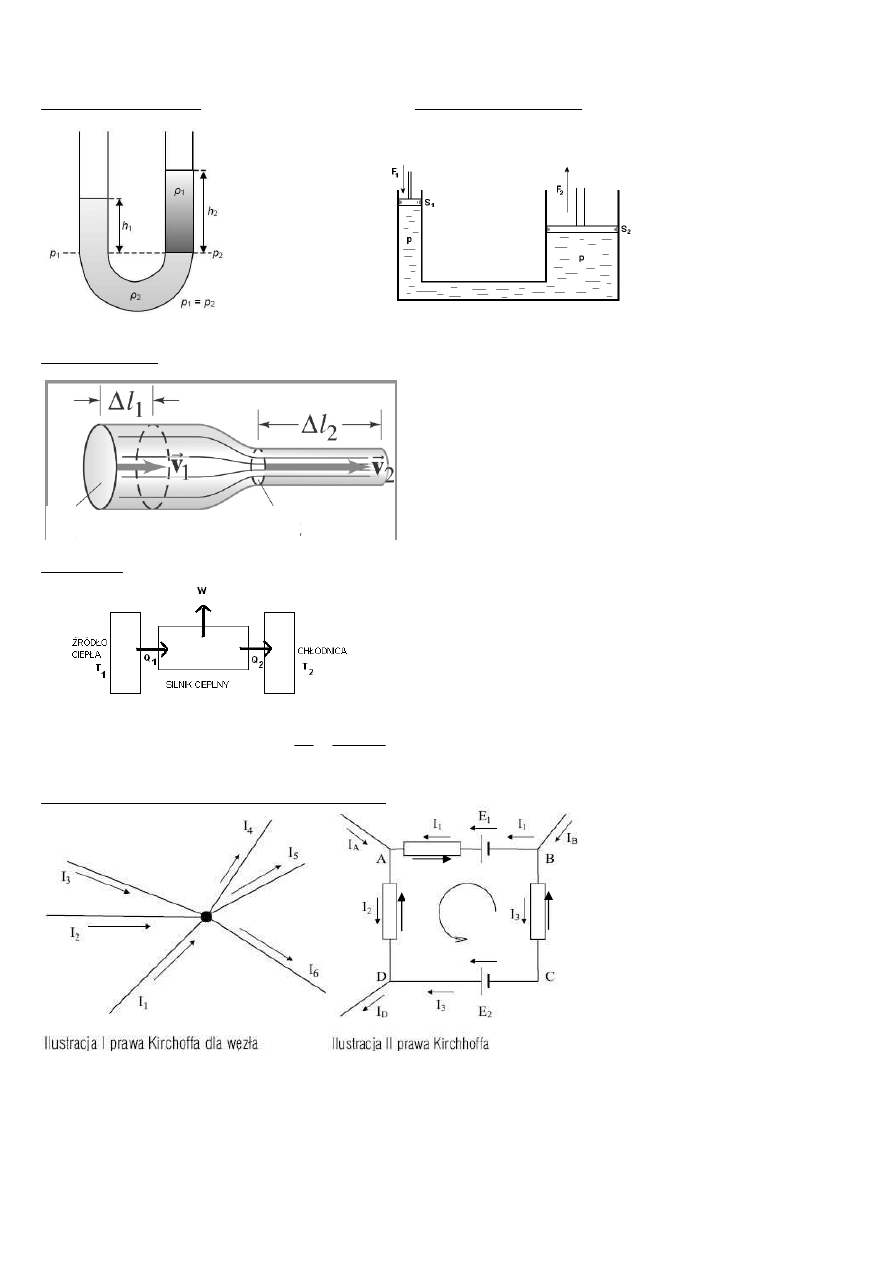
Prawo naczyń połączonych

Zastosowanie prawa Pascala

Ciągłość przepływu

Jeżeli ciecz płynie przez rurę ciągłym strumieniem, w tym samym
czasie

t w obu odcinkach rury musi płynąc taka sama objętość cieczy:

2

2

1

1

l

S

l

S

∆

⋅

=

∆

⋅

. Odległość ∆

l możemy przedstawić jako iloczyn

czasu

t i prędkości v:

t

v

S

t

v

S

⋅

⋅

=

⋅

⋅

2

2

1

1

. Ponieważ czas t jest dla

obu odcinków rury taki sam, po skróceniu uzyskujemy

2

2

1

1

v

S

v

S

⋅

=

⋅

Silnik cieplny

Silnik pobiera ciepło Q

1

z grzejnika o temperaturze T

1

. Część tego ciepła zamienia na pracę W. Resztę energii Q

2

oddaje do chłodnicy

o temperaturze T

2

. Sprawność silnika

1

2

1

1

Q

Q

Q

Q

W

−

=

=

η

Wykorzystanie praw Kirchoffa w obwodach elektrycznych

0

6

5

4

3

2

1

=

−

−

−

+

+

I

I

I

I

I

I

0

3

3

2

2

2

1

1

1

=

+

−

−

−

R

I

E

R

I

R

I

E

I

1

R

1

I

3

R

3

I

2

R

2

•

E

i

ma zwrot od ujemnej do

dodatniej elektrody

•

I

i

ma zwrot dowolny

•

I

i

R

i

(spadek potencjału na

oporze R

i

) ma zwrot przeciwny

do I

i

•

oczko ma zwrot dowolny

•

zwrot E

i

i I

i

R

i

jest dodatni, gdy

jest zgodny ze zwrotem oczka,
ujemny, gdy przeciwny do
zwrotu oczka

S

1

S

2

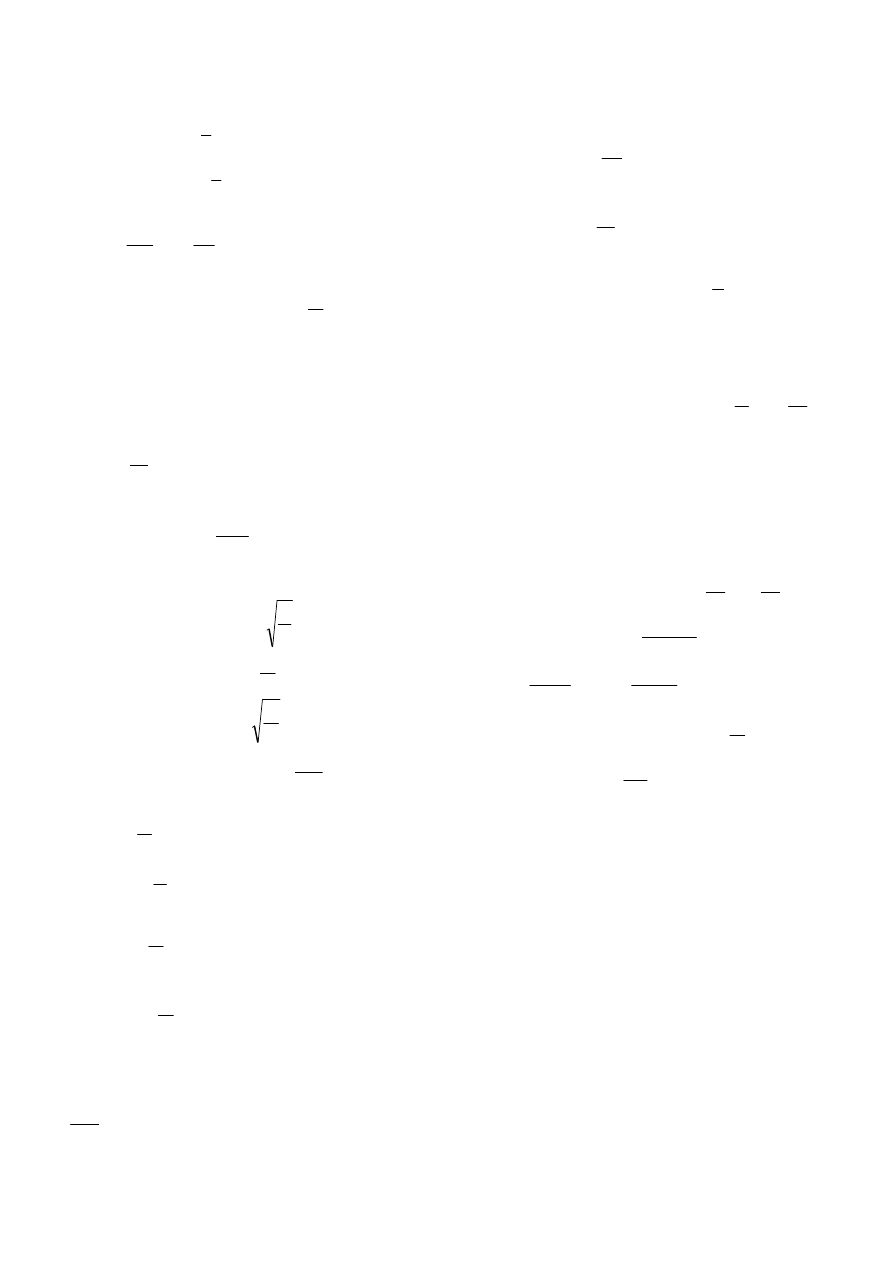
KINEMATYKA

Ruch jednostajny

t

s

v

=

Prędkość średnia

t

s

v

ś

r

=

Ruch jednostajnie przyspieszony

2

2

at

vt

s

+

=

,

t

v

a

∆

=

DYNAMIKA

Położenie środka masy na osi x

∑

=

=

n

i

i

i

m

ś

r

x

m

m

x

1

.

.

1

II zasada dynamiki Newtona

am

F

=

Ciężar

mg

F

=

Tarcie

fN

T

=

Moment siły

α

sin

⋅

=

Fr

M

Praca

α

cos

⋅

=

Fs

W

Moc

t

W

P

=

Energia potencjalna

mgh

E

=

Energia kinetyczna

2

2

mv

E

=

Pęd

mv

p

=

DRGANIA

Wahadło matematyczne

g

l

T

Π

=

2

Współczynnik sprężystości

x

F

k

=

Wahadło sprężynowe

k

m

T

Π

=

2

Energia potencjalna sprężystości

2

2

kx

E

=

FALE

Okres

f

T

1

=

Prędkość

T

v

λ

=

HYDROSTATYKA I HYDRODYNAMIKA

Gęstość

V

m

d

=

Siła wyporu

dVg

F

=

Ciśnienie

S

F

p

=

Ciśnienie hydrostatyczne

dhg

p

=

Równanie ciągłości przepływu

const

Sv

=

Równanie Bernoulli’ego (rura pozioma)

const

p

dv

=

+

2

2

TERMODYNAMIKA
Równanie Clapeyrona

nRT

pV

=

Liczba moli

M

m

n

=

Ilość ciepła

mc

Q

=

,

t

mc

Q

∆

=

Sprawność

E

W

=

η

ELEKTRYCZNOŚĆ

Natężenie prądu elektrycznego

t

q

I

=

Prawo Ohma

IR

U

=

Opór zastępczy, połączenie szeregowe

∑

=

=

n

i

i

R

R

1

Opór zastępczy, połączenie równoległe

∑

=

=

n

i

i

R

R

1

1

1

I prawo Kirchoffa

0

1

=

∑

=

n

i

i

I

II prawo Kirchoffa

0

)

(

1

1

=

+

∑

∑

=

=

n

i

i

i

n

i

i

R

I

ε

Moc prądu

UI

P

=

STAŁE

Przyspieszenie ziemskie

2

2

10

81

,

9

s

m

s

m

g

≈

=

Stała gazowa

K

mol

J

R

⋅

=

31

,

8

2

2

9

0

10

9

4

1

C

m

N

k

⋅

⋅

=

Π

=

ε

Prędkość światła w próżni

s

m

c

8

10

3

⋅

=

Gęstość wody

3

1000

m

kg

PRZEDROSTKI

Tera 'T' 10

12

= 1 000 000 000 000

Giga 'G' 10

9

= 1 000 000 000

Mega 'M' 10

6

= 1 000 000

Kilo 'k' 10

3

= 1 000

Hekto 'h' 10

2

= 100

Deka 'da' 10

1

= 10

Decy 'd' 10

-1

= 0, 1

Centy 'c' 10

-2

= 0, 01

Mili 'm' 10

-3

= 0, 001

Mikro 'm' 10

-6

= 0, 000 001

Nano 'n' 10

-9

= 0, 000 000 001

Piko 'p' 10

-12

=0, 000 000 000 001

Femto 'f' 10

-15

=0, 000 000 000 000 001