
Growing short rotation coppice on agricultural land in
Germany: A Real Options Approach
Oliver Musshoff
Georg-August-Universita¨t Go¨ttingen, Faculty of Agricultural Sciences, Department for Agricultural Economics and Rural Development,
Platz der Go¨ttinger Sieben 5, D-37073 Go¨ttingen, Germany
a r t i c l e i n f o
Article history:
Received 2 March 2011
Received in revised form
5 January 2012
Accepted 1 February 2012
Available online 28 March 2012
Jel classifications:
C6
D81
D92
Q12
Keywords:
Short rotation coppice
Optimal conversion strategy
Uncertainty
Sunk costs
Entrepreneurial flexibility
Real options Approach
a b s t r a c t
In many cases decision-makers apparently do not adapt as fast as expected to changing
economic conditions. This is also the case for the conversion of farm land to short rotation
coppice. From an economic point of view, short rotation coppice has become more inter-
esting in the last few years. Nevertheless, farm land still is rarely used to grow this quite
unknown crop. Several explanatory approaches (e.g., traditionalistic behavior and risk
aversion) are currently discussed in order to explain this behavior. A relatively new
explanatory approach is the Real Options Approach. The Real Options Approach uses
a comprehensive dynamic-stochastic model that combines the uncertainty of investment
returns, the sunk costs, and the temporal flexibility of the investment implementation. The
quintessence of the Real Options Approach is thatdcompared to the Classical Investment
Theorydthe investment triggers will be shifted upwards if investments involve inter-
temporal opportunity costs. This paper develops a real options model which allows the
determination of triggers on the basis of realistic assumptions. We examined when
farmers, who only dispose of sandy soils with little water-storing capacity, should convert
set-aside land to short rotation coppice. The results show that farmers should not convert
until the present value of the investment returns exceeds the investment costs consider-
ably. Thus, they confirm the empirically observed reluctance in conversion. Furthermore, it
turned out that the magnitude of the difference between the Classical Investment Theory
and the Real Options Approach depends heavily on the type of stochastic process that
underlies the investment returns.
ª 2012 Elsevier Ltd. All rights reserved.
1.
Introduction
For several years, the use of agricultural land for the cultiva-
tion of fast-growing tree species in a so-called short rotation
coppice (SRC) has been intensively discussed. This applies not
only to Germany but also to other European and North
American states. SRCs are permanent crops that allow the
extraction of solid biomass. According to the EU premium
rights and to the German Federal Forest Act, which was
changed concerning this matter in 2010, SRCs set up on agri-
cultural land do not fall within the definition of forest. Hence,
SRCs maintain the legal status of ‘agricultural areas’ as long as
the rotation period is not longer than 20 years.
Compared to the classical agricultural production methods
(e.g. wheat or canola) SRCs are less demanding regarding soil
quality and climatic conditions
. Moreover, when imple-
menting SRCs a comparatively stable physical yield can be
expected
. Against the background of finite non-renewable
* Tel.:
þ49 551 39 4842; fax: þ49 551 39 22030.
E-mail address:
oliver.musshoff@agr.uni-goettingen.de
.
Available online at
http://www.elsevier.com/locate/biombioe
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
0961-9534/$ e see front matter ª 2012 Elsevier Ltd. All rights reserved.
doi:

energy sources the use of wooden biomass from SRCs as
alternative energy source appears to be interesting
. Due to
higher energy costs the demand and the prices of such prod-
ucts have increased in recent years. In addition, with regards
to biodiversity, to soil protection against erosion as well as to
climate change, SRCs are assessed to be beneficial
. Recent
laws about renewable energies also set economic incentives
for the energy generation from SRCs. For instance, when
renewable raw materialsdsuch as wooddare used to
generate electricity, bonuses are paid
. Despite of these
developments, it has been observed that farmers convert even
poor locations, which can hardly be used for agricultural
production in an alternative way, only very hesitantly to SRCs.
In 2008, the area cultivated with SRC comprised only 1173 ha
throughout Germany
and, therefore, accounted only for
less than 0.01% of the total agricultural area in Germany.
There already are many studies that analyzed the on-farm
economic competitiveness of SRCs toward the classical use of
agricultural land. For example, Heaton et al.
examined the
competitiveness of SRCs in Mid-Wales, while Bemmann et al.
, Toews
as well as Wagner et al.
investigated this
matter in Germany. Thereby the farm’s individual decision to
convert to SRC is considered as an investment decision and
evaluated by referring to Classical Investment Theory in
general and the Net Present Value (NPV) in particular. On the
one hand, the conversion to SRC involves investment costs
that are at least partly sunk or irreversible. On the other hand,
due to the conversion to SRC the farm’s revenues and
expenditures are changing over a long period of time.
According to the NPV, profit-maximizers should convert to
SCR if the associated investment costs are covered by the
present value of the achieved investment returns. By applying
the Classical Investment Theory, Heaton et al.
, Styles et al.
and Wagner et al.
concluded that, from an economic
point of view, it might be beneficial for farms to convert to
SRC. All the more the question arises why do not convert more
and more farmers to SRC.
There are various explanatory approaches for the often
observed reluctance to convert. The latter could be caused, for
example, by traditionalistic behavior as well as by the
unusually long time that a piece of agricultural land is bound
by one specific crop through SRC. Furthermore, the farmers’
reluctance to convert could also be caused by risk aversion, by
open questions regarding technical production issues or by
missing liquid assets
. The Real Options Approach, which is
also called New Investment Theory, is an alternative explan-
atory approach
: Apart from the generation of sunk costs
the opportunity to invest in an SRC is characterized by the fact
that the incremental cash flow is stochastic. Moreover, there
is temporal flexibility regarding the implementation of the
conversion to SRC. In other words: the conversion to SRC can
be carried out today or in any year in the future. The Real
Options Approach evaluates entrepreneurial flexibility and
produces results that are different from the Classical Invest-
ment Theory: To put it simply, the investment threshold is
shifted upwards in case of temporal flexibility. At the end of
the day the investment returns do not only have to compen-
sate the investment costs but also the opportunity costs
meaning the profit that could be generated if the investment
would be postponed. The value of waiting is especially
pronounced if the investment returns are uncertain and the
investment would cause high sunk costs.
Some applications of the Real Options Approach can
already be found in the agricultural and forest economic
literature. For example, Pietola and Wang
as well as
Odening et al.
examine the decision to invest in a pig-
fattening farm in consideration of real options effects.
Kuminoff and Wossink
as well as Musshoff and Hir-
schauer
evaluate a farm’s opportunity to convert from
conventional to organic farming. Behan et al.
determine
the optimal time of conversion from agricultural production
to forest under consideration of temporal flexibility of the
investment implementation. Nevertheless, the uncertainty
regarding the conversion returns is left out of consideration in
the normative analysis. In the study of Wiemers and Behan
both the temporal flexibility as well as the uncertainty is
taken into account for the determination of the optimal time
of conversion from agricultural production to forest. Further
forestry studies determine the optimal length of the rotation
period of forests by applying the Real Options Approach
. The aforementioned studies illustrate that the results
of the Real Options Approach are partly significantly different
from those of the Classical Investment Theory.
So far, there are not any applications of the Real Options
Approach with regard to the question of the conversion to
SRC. In contrast to many classical agricultural production
methods, SRC does not provide a return each year. Further-
more, unlike many classical forestry production activities SRC
permits multiple harvests during its useful lifetime. In other
words: in existing studies about SRC the temporal flexibility of
the decision to convert as well as the uncertainty of the
investment returns were not considered. Consequently, it is
not clear yet at what time a farm should convert to SRC by
taking into account the real options effects as well as if the
Real Options Approach has a potential explanatory value for
the frequently observed reluctance of farmers to convert to
SRC.
Against this background, the overall aim of the present
study is to apply the Real Options Approach to SRC. The
following three sub-objectives arise: First, we want to help
farmers and/or foresters to determine whether or not they
should be using short rotation coppice as a new crop. To do so,
a real options valuation model is developed in the present
paper, which neither has been discussed in the literature nor
has been applied to agricultural or forest economic problems.
This model, which is based on a stochastic simulation and on
a parameterization of the investment trigger, can be used
regardless of the type of stochastic process, which underlies
the random variables (e.g. investment returns). Especially due
to the flexibility with respect to the type of stochastic process,
the developed real options valuation model has the potential
to be used as well in contexts other than the evaluation of the
decision to convert to SRC. Furthermore, we apply the real
options valuation model to an exemplary decision situation
with realistic assumptions. In this given situation a farm on
sandy soils in Northern Germany, which is also threatened by
drought, has the option to convert a so far set-aside agricul-
tural area to SRC. The conversion threshold and the options
value of the conversion to SRC are calculated by considering
the uncertainty, the irreversibility and the entrepreneurial
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
74

flexibility to defer the conversion. The results are compared to
those of the Classical Investment Theory. The risk aversion of
the decision-makers is taken into account by using risk-
adjusted interest rates. The determination of the differences
between the Real Options Approach and the Classical Invest-
ment Theory allows for conclusions on the practical relevance
of option effects. Herewith, we are able to analyze the expla-
nation potential of the Real Options Approach for the
frequently observed investment reluctance, which constitutes
our second sub-objective. The third sub-objective is to inves-
tigate the sensitivity of the modeling results with respect to
the assumed stochastic process of the uncertain variable. We
think that an open and unbiased estimation of stochastic
processes as well as the processing of the results of the real
options valuation would need more attention.
In the following, Section
briefly describes the theoretical
background of valuating real options. Subsequently, the
decision-making problem to be analyzed is explained in
Section
, while results are discussed in Section
. Finally,
conclusions are drawn from the results and potential future
research areas are described (Section
).
2.
Valuation of real options
The Real Options Approach combines uncertainty of invest-
ment returns, sunk costs and temporal flexibility with regard
to the investment’s implementation in a comprehensive
dynamic-stochastic model
. The approach is based on the
analogy between financial options and physical investments.
The option to invest now or to postpone the investment is
similar to American options: The owner of an American
option as well as the investor (e.g. the farmer or the forester)
has the rightdbut is not obligateddto choose to buy an asset
(e.g. a production facility) with an uncertain development (e.g.
present value of investment returns) within a certain time
period (lifetime of the option). The purchase of the asset is
associated with (fixed) investment costs.
According to the Classical Investment Theory, the value of
an investment at the time t is equivalent to the Net Present
Value NPV
t
, thus, the difference between the present value of
the revenues R
t
and the present value of the expenditures E
t
:
NPV
t
¼ R
t
E
t
(1)
In case of a positive Net Present Value, it would be recom-
mendable for the farmer to invest.
According to the financial options pricing theory, the clas-
sical Net Present Value, which is also called intrinsic value,
represents only one part of the total value of an investment
option [
:124]. Furthermore, an investment option has
a continuation value that is similar to the discounted expected
value of the investment at the next possible chance to invest.
Investing immediately means gaining the intrinsic value and,
at the same time, loosing the continuation value. A rational
investor will only invest immediately, if the intrinsic value
exceeds the alternatively achievable continuation value. The
Bellman equation for this binary decision-making problem is
defined as follows
: chapter 4]:
F
t
¼ max
NPV
t
;
mðNPV
t
þdt
Þ$ð1 þ iÞ
dt
(2)
F stands for the value of the investment option, i for the risk-
adjusted interest rate,
m(,) for the expectation operator and
max (
,) for the maximum operator. Hence, the Net Present
Value is a lower limit for the options value. Under specified
regularity conditions the stopping region, where the intrinsic
value exceeds the continuation value, and the continuation
region, where the continuation value exceeds the intrinsic
value, are clearly separated by a critical value for the
stochastic variable. With regard to investment options, the
latter is also called investment trigger. The regularity condi-
tions require that the intrinsic value and the continuation
value are monotonous functions of the value for the
stochastic variables. In addition, they require a positive
persistence of the stochastic process, meaning that the
distribution function of the uncertainty factors at the time
t
þ dt has to be shifted to the right (left) as soon as the value in t
increases (decreases)
:128].
The solution of Equation
is not trivial. Analytical solu-
tions exist only for simple valuation problems or special cases.
Preconditions include, for example, that the evaluated
investment option has an indefinite lifetime and a time
continuous opportunity to invest. Moreover, the present value
of the revenues has to follow a geometric Brownian motion
(GBM) and there should not be any interactions between the
investment option to evaluate and the other options (e.g.
reinvestment options and disinvestment options). If these
conditions are fulfilled, the McDonald-Siegel formula can be
applied
F
0
¼ ðR
E
0
Þ$
R
0
R
b
; with
R
¼
b
b 1
$E
0
and
b ¼
1
2
$
a
s
2
þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a
s
2
1
2
2
þ
2$lnð1 þ iÞ
s
2
s
(3)
In that formula
a indicates the drift rate, s the standard
deviation of the GBM and R* the critical present value of the
revenues, which triggers the investment. Since in case of an
option with an indefinite lifetime the entrepreneurial flexi-
bility remains constant, a time-independent critical value
indicates when the farmer should invest. The coefficient
b=ðb 1Þ given in Equation
, that is at
s > 0 generally greater
than one, is often also denoted investment multiple.
For many real options, the conditions of the analytical
solutions are not fulfilled, so that numerical-approximative
option valuation methods, such as the binomial tree method
or the stochastic simulation, need to be applied. Hull
provides an overview of several numerical option valuation
methods. The advantage of a simulation-based method is that
the value of an option at a given investment strategy can be
determined with relatively little effort, regardless how
complex the distributions of the stochastic variable are. Thus,
the time-discrete version of any stochastic process arising
after the implementation of an open-ended time series anal-
ysis for the stochastic variable can form the basis of the option
valuation method. It is not necessary to assume a GBM a pri-
ori, as often done in real options applications
:14]. The
disadvantage of the stochastic simulation is that it does not
contain any optimization algorithm. It is therefore only
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
75
possible to evaluate, for example, American options with
a limited term, whose optimal investment values are depen-
dent on the remaining lifetime, by combining stochastic
simulation with optimization algorithms
. In the event
that the investment option can be postponed indefinitely and
that therefore the optimal investment strategy corresponds
with a trigger, that remains constant over the whole lifetime
(see Equation
), we suggest performing the option valuation
by applying stochastic simulation as well as a parameteriza-
tion of the trigger.
To determine the optimal investment trigger and the
options value using stochastic simulation as well as parame-
terization of the trigger we apply the following procedure:
1. It is given a variety of test triggers. In addition, a parame-
terization range for the stochastic variable (e.g. the output
price) is chosen and divided into equal intervals. The upper
and lower limit of the parameterization range can be arbi-
trarily determined. It is also possible to use the investment
trigger according to the Classical Investment Theory as
lower limit.
2. For each given test trigger, the options value is determined.
That is, stochastic simulation is used to define the devel-
opment of the stochastic variable, while the options value
is calculated for each simulation run. In doing so, the initial
value of the stochastic variable should be varied from
simulation run to simulation run. The options value that is
obtained with the respective test trigger corresponds with
the options value obtained on average in all simulation
runs.
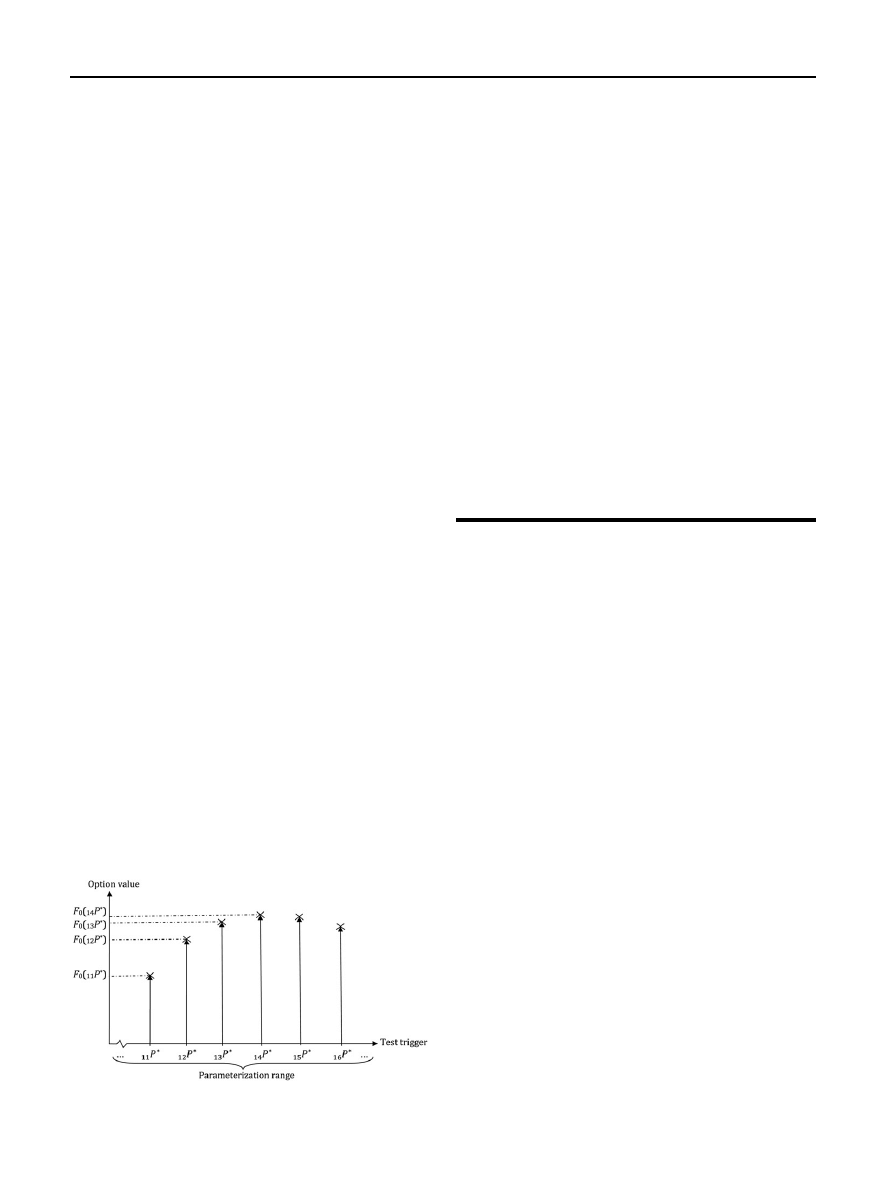
shows the relationship between the options
value and the test trigger. The figure subscripted on the left
of each P* indicates the number of the test trigger.
3. The test trigger that delivers the highest average options
value over all simulation runs is closest to the ‘true’ optimal
conversion threshold. In
,
14
P* provides the relatively
highest options value.
4. The potential solution space is ‘compressed’ in the direc-
tion of the real trigger and the options value is calculated
again. With a view to
, the test triggers
13
P* and
15
P*,
which are situated on the left and on the right of
14
P* are
defined as boundaries. The new test triggers are obtained
by dividing the parameterization range into equal intervals.
5. The approximation described in step 4 is if necessary
repeated several times and finally provides a more or less
smallddepending on the extent of the compressiondrange
for the critical value leading to maximum profit. In other
words: A more and more precise parameterization of the
critical value within a shrinking value range is performed.
6. The value of the investment option is defined on the basis
of the previously determined optimal investment trigger
and of the currently observed value of the stochastic
variable.
With a view to the result of the option valuation procedure
the following has to be taken into account: an option valuation
can be made independently of the decision-makers risk atti-
tude, if a replication portfolio of the assets can be formed that
corresponds with the stochastic results of the (dis)investment
project
: 241 ff.],
: 251 ff.]. On the one hand, this possi-
bility has to be examined on a case-by-case basis. On the other
hand, the recourse to the so-called risk neutral valuation
principle requires that a risk neutral drift is used for modeling
the stochastic variable and the risk-free interest rate is used
for discounting future payments. If the risk neutral valuation
principle cannot be applied, the results of the option valuation
apply only for the supposed risk attitude of the decision-
maker.
3.
A real options model for SRC conversion
3.1.
Description of the decision problem
The study examines exemplarily a farm in Northern Germany
that considers setting up an SRC. According to the relative
German soil quality classification scheme ranging from zero to
100 points the soil quality is 35 points. Furthermore, over the
years the precipitations reach on average only about 300 mm
in the relevant growth period from April up to and including
September. Groundwater is located at a depth of 4 m. The
available field capacity in the effective root zone is 220 mm.
The average annual temperature is approximately 8.5
C.
So far, the potential area for the SRC has been set-aside.
Due to the fact that it is not possible to generate any positive
gross margins because of the poor site conditions, no cereal or
the like is cultivated on that area. To preserve the acreage
payment that can also be obtained after the conversion to SRC
the area needs to be mulched once a year. The variable
costs associated with the mulching in the amount of 35
V ha
1
:151] could be saved when converting to SRC.
The area chosen for SRC can be planted with poplar
cuttings. In autumn, first, a total herbicide treatment is per-
formed to prepare the conversion of an agricultural area from
set-aside to SRC. In spring prior to planting, the area is plowed
and, subsequently, processed with a seedbed harrow. 9000
poplar cuttings per hectare are planted by machine. After
planting, once more a pre-emergence herbicide treatment is
carried out, in order to suppress competitive vegetation and to
facilitate an optimal growth for the cuttings. Estimated costs
for a non-selective herbicide treatment in autumn are
40
V ha
1
, costs for plowing might amount to 95
V ha
1
and
estimated costs for the seedbed harrow processing might
come to 40
V ha
1
. The price of one poplar cutting equals
0.25
V
, so that the costs of the cuttings would amount to
Fig. 1 e Stylized relationship between the option value and
the underlying investment strategy.
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
76
2250
V ha
1
. Costs for planting performed by the contractor
are estimated at 400
V ha
1
, while those for a pre-emergence
herbicide treatment are estimated at 50
V ha
1
. Conse-
quently, the total costs of a conversion to SRC would be
2875
V ha
1
.
During the useful lifetime of the SRC neither chemical
plant protection nor additional fertilization are used. More-
over, no protection measures regarding browsing by game are
adopted
. With respect to the rotation period (period of time
between planting and harvest or between two harvests) and to
the possible number of rotations or to the total useful lifetime
(period of time between planting and recultivation of the
acreage) various experiments with SRC confirmed the
following:
The annual increase in biomass rises over a period of time of
at least five years after planting or harvest
. However,
after a growth period of more than five years, automatic
harvest is only possible to a limited extent
. Thus the
optimal rotation period is five years
. In other forestry
contexts the determination of the optimal rotation period
often has to be treated as an important separate valuation
issue
The biomass yields increase significantly from the first to
the second rotation cycle and then remain more or less
constant
. For the described location annual increases
of on average 5 t dry matter (DM) ha
1
can be expected in the
first rotation period. In the following rotation periods annual
increases of on average 8 t DM ha
1
are expectable
Due to a decline in sprouting plants, a technologically more
difficult harvest because of a higher rootstock as well as to
a lower wood chip quality of the increasing number of the
thinning down sprouts, it is impossible or uneconomical to
run more than six rotation periods
. Consequently, six
rotation periods and a total useful lifetime of the SRC of 30
years are optimal.
At the end of each rotation period, costs for harvest, drying
and transport of the wood chips incur. These steps are per-
formed by a contractor at a price of 24
V t
1
DM
We assume that the marketing strategy for wood chips
produced in SRC is defined: Since the harvest-fresh wood has
a water content of approximately 55% that has to be reduced
for combustion, the wood chips are stored for three months at
the edge of the field using the dome aeration technology. The
wood chips are sold afterward
. With a nearby biomass
heating plant it is possible to conclude a supply contract for
the wood chips over a time period of 30 years at the time of
planting of an SRC. The wood chips have to be delivered every
five years.
So far, there is not any market for wood chips that has
worked properly in the long term. That is why in the supply
contract the wood chip price obtained by the farmer is linked
with the uncertain development of the heating oil prices. In
concrete terms, the price of one ton of dry matter of wood
chips corresponds with the price of 1000 l of heating oil
divided by 8.802 (
¼ 3 multiplied by 2.934). On the one hand, it is
taken into account that 3 kg of wood chips have the same
energy value as 1 l of heating oil
. On the other hand, it is
considered that the mean of the heating oil prices from 2003 to
2009 divided by three is 2.934 times higher than the mean of
the observed annual wood chips prices of that time
. The
correlation between the heating oil prices of the years 2003
and 2009 or the wood chip prices derived from them and the
actually obtained wood prices is 0.73. It is not possible to
obtain energy equivalent prices on the wood chip market
because inter alia the installation of a wood chip heating at the
end-user involves considerably higher costs than the
purchase of an oil heating
At the end of the SRCs useful lifetime, i.e. after 30 years, the
acreage needs to be recultivated. For the aforementioned
reasons this is even necessary if the area is meant to be
recultivated with an SRC. The cost for recultivation by means
of stump pulling amounts to 1400
V ha
1
We assume that the observed farm can convert from
setting-aside the land to SRC within an indefinite time period.
The decision to convert can be made once a year. Moreover, it
is possibledbut not compulsorydto reinvest in an SRC after
the expiration of a SRCs useful lifetime. The farmer can
therefore omit to reinvest in an SRC and can use the area again
as set-aside land. In case of conversion to SRC, the wood chips
production will have to be maintained over 30 years, due to
the supply contract concluded with the biomass heating
plant. In other words: If the conversion to SRC has been
completed, the farmer is bound to this production method for
30 years and there is not any flexibility to recultivate the SRC
before the end of its useful lifetime.
3.2.
Modeling of the uncertain conversion returns
Besides the investment costs the profitability of converting to
SRC depends on the development of the payments caused by
the investment in SRC. Area-related direct payments are not
relevant for the decision since it is granted for set-aside land
as well as for SRCs. Concerning this matter, a possibly varying
political uncertainty is not considered. The future heating oil
prices or wood chips prices derived from the former and
relevant for the amount of the revenues from the SRC are
fraught with uncertainty.
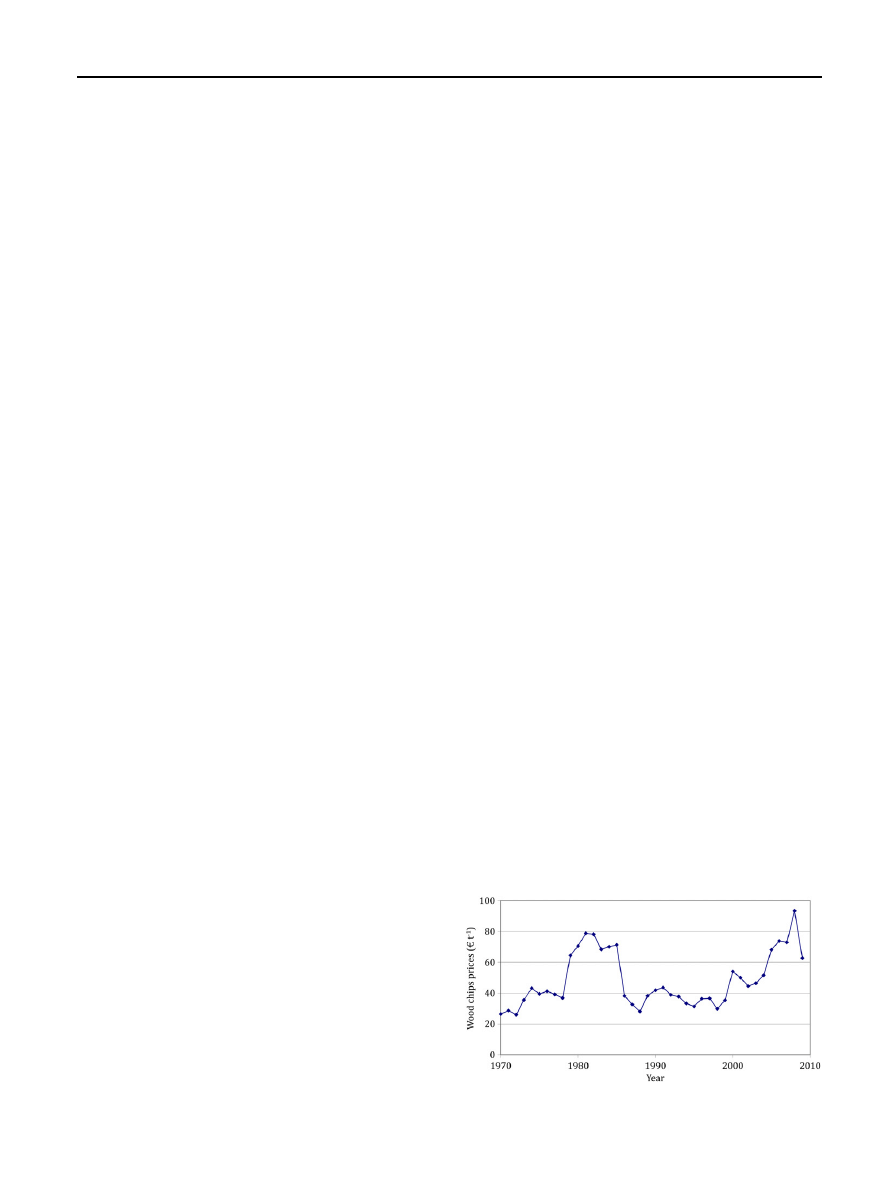
shows the development of the
wood chips prices over the time period between 1970 and
2009. These prices are derived from the heating oil prices at
that time
.
With a view to
it becomes clear that these inflation-
adjusted
wood
chips
prices
have
been
subject
to
Fig. 2 e Development of the wood chips prices derived from
heating oil prices (inflation-adjusted).
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
77

considerable fluctuations within the observed period of time.
They fluctuate between 25.95
V t
1
DM in 1972 and 93.40
V t
1
DM in 2008. The wood chips prices are assumed to be the only
stochastic variable in the model. The yields of the SRC are not
assumed as stochastic variable because yield is built up over
several years and is in case of appropriate groundwater supply
anyway less dependent on precipitations than, for example,
the yield of traditional cereal production
.
In connection with the modeling of the development of
stochastic variables, stochastic processes become more and
more important. The term ‘stochastic process’ implies that
assumptions about the probability distribution of stochastic
variables are made at different times in the future. By means
of time series analysis the attempt is being made to obtain the
distribution information of
by identifying the ‘best’
stochastic processes. For this purpose, first of all, the
Augmented-Dickey-Fuller-Test
as well as the Variance-
Ratio-Test
are applied to analyze stationarity. The
consistent result of both tests is that the wood chips prices are
non-stationary (significance level of 5%).
The GBM is a plausible non-stationary process for the price
development modeling: It is ensured that the stochastic
variable cannot change the sign meaning that in case of
a positive initial value no negative values can occur. Moreover,
the BoxeJenkins test procedure
confirms that the wood
chips prices follow a Random-Walk process. Furthermore, the
GBM is the default option for the modeling of the development
of the stock price. Postali and Picchetti
provide empirical
evidence for the fact that the GBM can approximate correctly
the oil price development. The GBM can be expressed math-
ematically in discrete time as follows:
P
t
¼ P
t
Dt
$e
½ð
a0:5$s
2
Þ
$Dtþs$
ffiffiffiffi
Dt
p
$ε
t
(4)
P
t
indicates the wood chips price at the time t,
a the drift
rate,
s the standard deviation of the relative logarithmic
change in value of the wood chips prices and
ε
t
a standard
normally distributed random number. A comparison of
means of the relative logarithmic changes in value of the
wood chips prices shows that the drift rate does not differ
significantly from zero ( p-value
¼ 0.514; two-sided t-test).
Thus,
a is equal to 0% a
1
. The standard deviation
s is
21.05% a
1
(standard error
¼ 3.37%). The GBM contains the
Markov property meaning that the probability distribution of
the future wood chips prices is exclusively dependent on the
last value observed.
The expectation value of a stochastic variable following
a GBM can be calculated as follows
mðP
t
Þ ¼ P
t
Dt
$e
a$Dt
(5)
However, it has to be considered that a drift rate of zero does
not mean that the stochastic variable tends to zero during the
time observed. It rather describes the fact that the expected
relative logarithmic change in value equals zero and that
therefore the expectation value of the future wood chips pri-
ces equals the currently observed value.
While it seems plausible to assume a GBM for modeling
stock prices, this is not necessarily the case for commodity
prices or revenues as well as gross margins of real invest-
ments. Using variant calculations we therefore examine to
what extend the choice of an alternative stochastic process
influences the results. We look at a linear version of the GBM
meaning that we analyze an arithmetic Brownian motion
(ABM) that is suggested, for example, by Dixit and Pindyck
65 ff.] for the valuation of real options and that can especially
be relevant for modeling non-stationary cash-flows. The ABM
can be expressed mathematically in discrete time as follows:
P
t
¼ P
t
Dt
þ a$Dt þ s$
ffiffiffiffiffi
Dt
p
$ε
t
(6)
In the equation above
a indicates the drift and s the stan-
dard deviation measured respectively in
V t
1
DM. A
comparison of means of the absolute changes in value of the
wood chips prices shows that also the drift of the ABM does
not significantly differ from zero ( p-value
¼ 0.601; two-sided t-
test). The standard deviation
s is 11.03 V t
1
DM. For the
expectation value of a stochastic variable the following
applies:
mðP
t
Þ ¼ P
t
Dt
þ a$Dt
(7)
When assuming an ABM a sign change of the stochastic
variable cannot be excluded. Hence, due to theoretic consid-
erations the ABM is not plausible for modeling price
developments.
Although the Augmented-Dickey-Fuller-Test for the pres-
ently analyzed wood chips prices shows that the stationary
assumption does not apply, we model the logarithmic wood
chips prices in a further variational calculus. There are three
reasons for do so: First, for many economic variables it seems
plausible to assume that in the long term there is an equilib-
rium level around which their value fluctuates temporarily.
Attention is paid to the relationship between the product
prices and the long term production costs. Thus, in the long
run prices are approximating the production cost level. The
more they have diverged from that level, the higher is the
probability of return. Such behavior of a stochastic variable
can be modeled by (stationary) Mean-Reverting-Processes
(MRP) that can also be understood as a special case of a first-
order autoregressive process. Second, in the literature it is
stated that MRP can only be identified if very long time series
over a period of e.g. 100 years are available
: 510e511]. Our
time series only covers 40 observations, which might be too
low to identify an MRP. Third, Baker et al.
as well as Pili-
povic
provide empirical evidence for the assumption that
oil prices follow an MRP.
We use an Ornstein-Uhlenbeck-Process which is a special
MRP that can be expressed mathematically in discrete time as
follows
:
x
t
¼ x
t
Dt
$e
h$Dt
þ x$
1
e
h$Dt
þ s$
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
e
2$h$Dt
2$h
s
$ε
t
(8)
In the aforementioned equation x
t
¼ ln (P
t
).
h indicates the
speed of return of the stochastic variable x to its equilibrium
level of x. The logarithmic wood chips prices show the
following characteristics:
h ¼ 0.22, x ¼ 3:92, and s ¼ 0.22. The
expectation value for x
t
in accordance with MRP can be
determined as follows:
mðx
t
Þ ¼ x
t
Dt
$e
h$Dt
þ x$
1
e
h$Dt
(9)
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
78
In contrast to Brownian motions, the expected change in
value can be positive (when x
t
Dt
< x), zero (when x
t
Dt
¼ x) or
negative (when x
t
Dt
> x). For the expected price based on m (x
t
)
applies:
mðP
t
Þ ¼ e
mðx
t
Þþ0:5$Varðx
t
Þ
; with
Var
ðx
t
Þ ¼ ð1 e
2$h$Dt
Þ $
s
2
2$h
(10)
Var(x
t
) indicates the variance of x
t
.
m (P
t
) converges toward
53.37
V t
1
DM.
3.3.
Evaluation of the conversion decision within the
classic investment theory
First of all, it is assumed in accordance with the Net Present
Value that a farm can convert from set-aside to permanent
SRC ‘now or never’. At an expected wood chips price that
remains constant over time
m(P
0
)
¼ m(P
1
)
¼ m(P
2
)
¼ . ¼ P the
present value of the revenues can be calculated as follows:
R
0
¼ r
n
$
1
i
ðp ¼ sÞ
ðr
n
r
s
Þ $
1
i
ðp ¼ NÞ
$ð1 þ iÞ
N
s
; with
r
s
¼ Q
s
$P und r
n
¼ Q
n
$P
(11)
Q
s
(r
s
) indicates the starting level of output (revenues) in the
starting rotation period of the SRC and Q
n
(r
n
) the normal level
of output (revenues). Furthermore, i describes the annual
adequate target rate, i( p
¼ s) the adequate target rate for
a discount period p in the amount of the rotation period
s as
well as ( p
¼ N ) the adequate target rate for a discount period
in the amount of the useful lifetime N of an SRC. There is the
following relationship between the annual interest rate i and
the interest rate i ( p) referring to a time period p in years:
i
ðpÞ ¼ ð1 þ iÞ
p
1
(12)
By using the first component of Equation
, the present
value of an infinite annuity that would result from constant
revenues at the normal level is calculated. The second
component takes account of the lower revenues of the first
rotation period of an SRC.
The investment costs IC involved in setting up an SRC is to
rise in year zero as well as in each of the following N years. The
present value of the investment costs is calculated as follows:
IC
0
¼ IC þ IC$
1
i
ðp ¼ NÞ
(13)
For the present value of the harvesting, drying and trans-
portation costs HC
0
applies analogously to Equation
HC
0
¼ hc
n
$
1
i
ðp ¼ sÞ
ðhc
n
hc
s
Þ $
1
i
ðp ¼ NÞ
$ð1 þ iÞ
N
s
; with
hc
s
¼ Q
s
$HC and hc
n
¼ Q
n
$HC
(14)
HC indicates the sum of the harvesting, drying and trans-
portation costs in
V t
1
DM.
Moreover, recultivation costs RC accrue in each of the
N years. For the present value of the recultivation costs RC
0
applies:
RC
0
¼ RC$
1
i
ðp ¼ NÞ
(15)
Furthermore, the annual set-aside costs SC are relevant.
They can be saved in case of a conversion to SRC. The present
value of the set-aside costs SC
0
equals:
SC
0
¼ SC$
1
i
(16)
The present value of the expenditures can be calculated as
follows:
E
0
¼ IC
0
þ HC
0
þ RC
0
SC
0
(17)
For the Net Present Value applies (see Equation
NPV
0
¼ R
0
E
0
(18)
On the basis of the Equations
, the (critical) present
value of the revenues R*
M
as well as the (critical) wood chips
price P*
M
can be determined. Both figures lead to a Net Present
Value of zero and therefore, define the conversion threshold.
The subscript M on the right refers to the investment
thresholds that in the context of the NPV are often called the
Marshallian-Triggers.
When working with an annual adequate target rate in the
amount of the risk-free interest rate, the decision-maker is
assumed to be risk neutral. The risk-free interest rate can be
deduced from the return of quoted quasi secure German
federal bonds. The mean of the nominal return of the German
federal bonds with a residual lifetime of more than 15e30
years from 1988 to 2009 is 5.92% a
1
. In the same period,
the inflation rate stood at 1.98% a
1
. We use the corre-
sponding real interest rate of 3.87% a
1
as proxy for the risk-
free interest rate.
It is hard to assume that entrepreneurs are risk neutral.
They are more or less risk-averse. The consideration of the
risk attitude can be ensured in the investment planning, for
example, through risk-adjusted discount rates. In the Risk-
Adjusted-Discount-Rate-Approach, a risk-adjusted interest
rate is determined subjectively in accordance with the risk
aversion of the decision-maker. Due to the difficulties of the
empirical determination of a decision-maker’s risk premium
, the risk premium is often parameterized
. In
accordance with this, we carry out variant calculations in
order to test how the optimal conversion strategy changes
with the risk attitude of the decision-maker. The following
mathematical relationship applies:
i
¼ rf þ r
(19)
i describes the risk-adjusted interest rate, rf the risk-free
interest rate and
r the risk premium that is added to the
risk-free interest rate. To examine the general effects of risk
aversion, we use three risk-adjusted interest rates: 3.87% a
1
(risk neutral), 8.87% a
1
(risk-averse) and 13.87% a
1
(strongly
risk-averse). The level of the risk premium is varied by 0%e
10% in accordance with the literature, which often mentions
risk premiums in the amount of 8%e12%
3.4.
Evaluation of the conversion decision within the
Real Options Approach
In contrast to the NPV, the Real Options Approach considers
the combined effect of the uncertainty of the investment
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
79

returns, the irreversibility of the investment costs and the
temporal flexibility of the investment implementation that is
relevant with respect to the conversion from agricultural
production to SRC. In case wood chips prices follow a GBM, the
investment option has an indefinite lifetime, and a time
continuous exercise opportunity exists as well as there are no
interactions between different options, Equation
could be
used to determine the options value and the critical exercise
value. However, in our case the preconditions for applying
Equation
are not fulfilled. Therefore, we have to value the
option using a numerical method.
The future returns can be calculated as follows:
In words, Equation
can be described as follows:
There will not be any changes in the revenues and expen-
ditures (S
t
¼ 0) if the land use has so far been set-aside
(LU
t
¼ 0) and the stochastic wood chips price P
t
is lower
than the trigger price P* (P
t
< P*) meaning that the land use is
also set-aside in the next period (LU
t
þ1
¼ 0).
S
t
corresponds with the expenditures in the amount of the
investment costs for an SRC (S
t
¼ IC) if the land has so far
been used as set-aside (LU
t
¼ 0) and the stochastic wood
chips price P
t
is above or equal to the trigger price P* (P
t
P*)
meaning that the land use will be converted to SRC
(LU
t
þ1
¼ 1).
S
t
corresponds with the output Q
s
that is connected to the
first rotation period of the SRC, multiplied by the difference
between the wood chips price P
t
and the harvesting, drying
and transportation costs HC plus the saved set-aside costs
SC. This is the case if the land is used as SRC (LU
t
¼ 1) and the
year of use N
jt
of the SRC j at the time t corresponds with the
rotation period
s(N
jt
¼ s).
S
t
corresponds with the output Q
n
multiplied by the differ-
ence between the wood chips price P
t
and the harvesting,
drying and transportation costs HC plus the saved set-aside
costs SC. This is the case if the land is used as SRC (LU
t
¼ 1)
and the respective SRC is harvested in all rotation periods
from
the
second
to
the
second
last
period
T
(N
jt
¼ 2$sn/n N
jt
¼ ðT 1Þ$s).
S
t
corresponds with the output Q
n
multiplied by the differ-
ence between the wood chips price P
t
and the harvesting,
drying and transportation costs HC plus the saved set-aside
costs SC and less the recultivation costs RC. This is the case
if the land is used as SRC (LU
t
¼ 1), the respective SRC is
harvested for the last time (N
jt
¼ T$s) and the stochastic
wood chips price P
t
is lower than the trigger P* (P
t
< P*)
meaning that the land is set-aside again after the useful
lifetime of the SRC.
S
t
corresponds with the output Q
n
multiplied by the differ-
ence between the wood chips price P
t
and the harvesting,
drying and transportation costs HC plus the saved set-aside
costs SC and less the recultivation costs RC as well as the
investment costs IC of a new SRC. This is the case if the land
is used as SRC (LU
t
¼ 1), the respective SRC is harvested for
the last time (N
jt
¼ T$s) and the stochastic wood chips price
P
t
is higher or equal to the trigger P* (P
t
P*) meaning that the
area will continue to be used as SRC after the expiration of
the useful lifetime of the previous SRC.
S
t
corresponds with the saved set-aside costs SC if the area
is cultivated with SRC but is not harvested at the respective
point in time.
For the determination of the critical wood chips price P*,
the objective function F
0
that corresponds with the value of
the conversion opportunity respectively with the options
value has to be maximized. The stochastic-dynamic invest-
ment planning problem can formally be expressed as follows:
F
0
¼
X
N
t
¼0
S
t
ðP
Þ$ð1 þ iÞ
t
/ max!
P
(21)
To calculate the options value, it is necessary to determine
the present value of the future investment returns S
t
obtained
at optimal conversion strategy during the planning period t
(t
¼ 0,1, ., N).
Due to the fact that it is not possible to develop a replica-
tion portfolio (see Section
) for the examined decision situa-
tion including the above-mentioned individual supply
contract of the wood chips over 30 years, the annual adequate
target rate i is also varied in the real options valuation. As with
of the NPV, a risk neutral decision-maker (i
¼ 3.87%), a risk-
averse decision-maker (i
¼ 8.87%) and a strongly risk-averse
decision-maker (i
¼ 13.87%) are examined.
The maximizing problem described in Equation
corre-
sponds with the determination of the value of an American
option with an indefinite lifetime. Due to the fact that for the
disaggregated variable ‘wood chips price’, to which the
uncertainty regarding the investment returns can be attrib-
uted to, a GBM is plausible, it is also possible to model the
present value of the revenues by using a GBM featuring the
same process parameters. Hence, at first it seems to be
reasonable to refer to Equation
for option valuation.
Nevertheless, realistically, on the one hand, there is not any
time continuous opportunity to convert to SRC and, on the
S
t
ðP
Þ ¼
8
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
:
0
; if LU
t
¼ 0 L P
t
< P
IC; if LU
t
¼ 0 L P
t
P
Q
s
$ðP
t
HCÞ þ SC; if LU
t
¼ 1 L N
jt
¼ s
Q
n
$ðP
t
HCÞ þ SC; if LU
t
¼ 1 L N
jt
¼ 2$s V.V N
jt
¼ ðT 1Þ$s
Q
n
$ðP
t
HCÞ þ SC RC; if LU
t
¼ 1 L N
jt
¼ T$s L P
t
< P
Q
n
$ðP
t
HCÞ þ SC RC IC; if LU
t
¼ 1 L N
jt
¼ T$s L P
t
P
SC
; otherwise
(20)
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
80

other hand, after setting up one SRC there is again the chance
to set up another one. Therefore, it is not possible to evaluate
the conversion to SRC analytically. The time continuous
investment opportunity implied in Equation
causes the
overestimation of the investment trigger and the options value
(more entrepreneurial flexibility). The reinvestment opportu-
nity that is not considered in Equation
has an opposite
effect (less entrepreneurial flexibility). The significance of the
respective effect cannot be assessed offhand. Therefore, the
simulation-based option valuation method described in
Section
is applied. This method can be validated for the
special case that can be solved by means of Equation
.
If we apply the simulation-based options valuation proce-
dure in order to determine the thresholds and the options
values for the conversion from agricultural production to SRC,
an indefinite planning period has to be approximated through
a finite value as with all numerical valuation procedures. We
look at a period of time of 500 years. The resulting approxi-
mation error can be assessed as small because the present
value of, for instance, 100,000
V, which are achieved in 500
years at an interest rate of 3.87%, amounts to less than 1 cent.
We refine the parameterization interval of the conversion
trigger to up to 0.20
V t
1
DM and use MS-EXCEL to perform
50,000 simulation runs for the determination of the options
values. Haug
:140], for example, suggests performing at
least 10,000 simulation runs
.
4.
Results
shows the optimal conversion strategies according to
the Classical Investment Theory and to the Real Options
Approach assuming GBM, which according to statistical tests
best describes the development of the wood chips price.
Furthermore, Net Present Values and options values resulting
from a wood chips price of 62.76
V t
1
DM observed in 2009 are
indicated. In line 1 we look at a risk neutral decision-maker,
which uses the risk-free interest rate for discounting future
payments. The results have to be interpreted as follows:
The columns 5 to 7 show the results that would emerge if
the temporal flexibility regarding the conversion to SRC is
not taken into account (‘now-or-never-decision’). By looking
at column 5 it becomes clear that a risk neutral decision-
maker should convert to SRC if the wood chips price is
higher than or equal to 47.0
V t
1
DM (equals 0.41
V l
1
of
heating oil). The corresponding critical present value of the
revenues of 8137
V ha
1
(column 6) is equivalent to the
present value of the expenditures (column 3). From the
current wood chips price of 62.76
V t
1
DM would result
a present value of revenues of 10,862
V ha
1
and, therefore,
in the event of conversion a Net Present Value of
2725
V ha
1
. Consequently, given a wood chips price of
62.76
V t
1
DM, the conversion to SRC would be profitable
and therefore should be implemented.
The columns 8 to 11 show the results if the conversion can
be postponed and accepted annually. Compared to the
‘now-or-never-decision’ significant differences emerge. A
risk neutral decision-maker, for example, should only
convert immediately to SRC, if the present wood chips price
is higher than or equal to 73.6
V t
1
DM (equals 0.65
V l
1
of
heating oil). Only in case of a wood chips price of that height,
no higher expected Net Present Value would emerge at any
later stage. The critical present value of the revenues is
12,739
V ha
1
. Hence, it would be favorable for risk neutral
farmers to convert at a present value of the revenues that is
1.57 times higher than the present value of the expenditures
(investment multiple; column 11). In case of the current
wood chips price of 62.76
V t
1
DM the options value
amounts to 4317
V ha
1
. At a wood chips price of
62.76
V t
1
DM it therefore would not be recommendable to
convert immediately. To convince risk neutral farmers to
convert to SRC, it would be necessary to pay monetary
incentives in the amount of the values of waiting, meaning
at least 1592
V ha
1
(
¼ 4317 V ha
1
e2725 V ha
1
).
To illustrate the consequences of higher investment costs
for SRC, line 2 indicates the results in case of twice as high
investment costs (5750
V ha
1
). It becomes clear that accord-
ing to both the Classical Investment Theory and to the Real
Options Approach the conversion threshold increases
together with the investment costs. The investment multiple,
however, remains constant at 1.57. Marginal differences result
from the parameterization area as well as from the fact that
the figures were randomly drawn. This is also confirmed by
further variant calculations regarding the investment costs. In
other words: If the investment multiple is known, the
Table 1 e Overview of the assumed model parameters
a
(applicable to classical investment model and real
options model).
Investment costs for an SRC IC:
2875
V ha
1
Harvesting, drying and
transportation costs HC:
24
V t
1
DM
Rotation period
s:
5 years
Number of rotation periods T:
6
Useful lifetime of an SRC N:
30 years
Output of the SRC
In 1. rotation period after
setting up Q
s
:
25 t DM ha
1
In 2. to 6. rotation period
after setting up Q
n
:
40 t DM ha
1
Recultivation costs for an
SRC RC:
1400
V ha
1
Potential implementation
period for the conversion:
N (annual implementation
right and reinvestment
opportunity in SRC)
Risk-free interest rate rf:
3.78% a
1
Risk premium
r:
0% a
1
(risk neutral
decision-maker)
Stochastic process for the
wood chips prices:
Geometric Brownian
motion (GBM)
Process parameters
Drift rate
a:
0% a
1
Standard deviation
s:
21.05% a
1
Annual disposable set-aside
costs SC:
35
V ha
1
Currently observed wood
chips price P
0
:
62.76
V t DM
a In variant calculations the sensitivity of the results is examined
with regard to (i) the amount of the investment costs IC, (ii) the
amount of the risk premium
r and (iii) the type of the underlying
stochastic process.
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
81

conversion thresholds at different investment costs can be
determined easily under the assumption of a GBM.
To illustrate the effect of risk aversion, the consequences
for decision-makers with different risk attitudes are indicated
in line 3 and 4. It becomes clear that:
A risk-averse decision-maker, who uses an interest rate of
8.87% for discounting future payments (line 3) and who, in
addition, ignores the temporal flexibility, should convert to
SRC if the wood chips price is higher than or equal to
67.8
V t
1
DM. In accordance with the commonly known
statement that risk aversion induces investment reluctance,
a risk-averse decision-maker would only make a risky
investment in case of a higher wood chips price. The present
value of the revenues of 4400
V ha
1
, which would result
from a wood chips price of 67.8
V t
1
DM, however, is
equivalent to the present value of the expenditures. In other
words: With regard to the critical present value in case of
a ‘now-or-never-decision’ the same decision rule applies to
decision-makers with diverse risk attitudes. In case of the
current wood chips price of 62.76
V t
1
DM the Net Present
Value of the risk-averse decision-maker would amount to
327 V ha
1
. Hence, it would not be attractive for a risk-
averse decision-maker to convert to SRC. For a risk-averse
decision-maker, who works with a risk-adjusted interest
rate of 13.87% (line 4) these effects even amplify.
When taking into account the temporal flexibility regarding
the conversion to SRC for a risk-averse decision-maker and
comparing the results to that of a risk neutral decision-
maker (line 1), it becomes apparent that the critical wood
chips price rises in the former case. Nevertheless, the
investment multiple falls in comparison to a situation in
which only the temporal flexibility is taken into account and
not at the same time the risk aversion (1.57 vs. 1.42 or 1.34).
In other words: the delay of a per se profitable investment
(in case of a high wood chips price) is less advantageously at
a higher discounting rate. In addition, it becomes clear that
the opportunity to convert is of less value for a risk-averse
decision-maker than for a risk neutral one assuming
conditions being equal.
The results indicated in line 5 refer to a situation in which
the farmer could decide only once to cultivate SRC on a certain
agricultural area for 30 years. In this case there would not be
any further reinvestment options. Assuming that the setting
up of an SRC also involves costs in the amount of 2875
V ha
1
the present value of the expenditures would fall from
8137
V ha
1
(including reinvestment, line 1) to 5532
V ha
1
.
When ignoring temporal flexibility regarding the time of
conversion, the same critical wood chips price of 47.0
V t DM
results from that ceteris paribus comparison. Taking into
account that it is also possible once to convert to SRC at a later
point in time, the critical wood chips price rises to
87.6
V t
1
DM and therefore increases more significantly than
in case of further reinvestment options. If the farmer has only
one single chance to convert, the investment multiple is 1.86.
Consequently, the results indicated in line 5 make clear, on
the one hand, that the farmers’ reluctance to convert would be
overestimated if the realistically possible repeated reinvest-
ment options are not taken into account. On the other hand,
Table
2
e
Crit
ical
wood
chips
prices,
cri
tical
present
values
of
reven
ues
and
value
of
con
version
oppo
rtunitie
s
assuming
GBM.
Col
umn
1
Col
umn
2
Column
3
Col
umn
4
Col
umn
5
Colum
n
6
Colum
n
7
Co
lumn
8
Column
9
Col
umn
10
Colum
n
11
As
sumptio
ns
Without
temp
oral
flexib
ility
(cl
assical
inves
tment
theor
y)
With
temp
oral
flexib
ility
(Re
al
Optio
ns
App
roach)
Inves
tmen
t
multi
ple
R
=R
M
Re
investme
nt
option
Inves
tmen
t
costs
of
an
SR
C
(V
ha
1
)
Pre
sent
value
of
the
ex
pend
itures
a
(V
ha
1
)
Inter
est
rate
(%
a
1
)
Critica
l
wood
chip
s
pric
e
P
M
(V
t
1
DM)
Critica
l
presen
t
value
of
the
reven
ues
R
M
(V
ha
1
)
Net
Pre
sent
Valu
e
NPV
0
c
(V
ha
1
)
Critica
l
wood
chips
price
P
*
b
(V
t
1
DM
)
Critical
prese
nt
value
of
the
rev
enues
R
*
(V
ha
1
)
Optio
ns
va
lue
F
0
c
(V
ha
1
)
1
With
2875
8137
3.87
47.0
8137
2725
73.6
12,739
4317
1.57
2
With
5750
12,366
3.87
71.5
12,366
1504
112.0
19,385
3005
1.57
3
With
2875
4400
8.87
67.8
4400
327
96.0
6231
678
1.42
4
With
2875
3569
13.87
99.9
3569
1325
133.4
4768
131
1.34
5
Without
2875
5532
3.87
47.0
5532
1852
87.6
10,308
2545
1.86
a
Present
value
of
the
investment
costs
plus
the
present
value
of
the
harvesting,
drying
and
transportation
costs
of
the
wood
chips
plus
the
present
val
ue
of
the
recultivation
costs
minus
the
present
value
of
the
saved
setting-aside
costs
by
the
conversion
to
SRC.
In
the
case
which
includes
reinvestment
options
a
permanent
cultivation
with
SRC
is
as
sumed.
b
The
parameterization
interval
of
the
conversion
trigger
is
refined
to
up
to
0.20
V
t
1
DM.
c
The
Net
Present
Value
and
options
value
have
been
calculated
for
an
initial
wood
chips
price
of
P
0
¼
62.76
V
t
1
DM;
50,000
simulation
runs.
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
82

the results indicated in line 5 allow of a validation of the used
simulation-based real options valuation model. On the basis
of the analytical solution described in Equation
, the critical
present value of the revenues as well as the option price,
which apply in case of a time-continuous option to convert,
can be determined. From a present value of the expenditures
of 5532
V ha
1
results a critical present value of the revenues
of 11,669
V ha
1
, which corresponds with a critical wood chips
price of 99.2
V t
1
DM. At a current wood chips price of
62.76
V t
1
DM the options value amounts to 2572
V ha
1
. Due
to the fact that in the analytical solution it was assumed
implicitly that it is permanently possible for farmers to
convert to SRC, implying additional entrepreneurial flexibility,
both the critical values as well as the options values are
slightly higher than those indicated in line 5. In the light of
that, the results of the numerical option valuation procedure
seem to be valid.
The comparison of the results indicated in
, on the
one hand, clarifies the flexibility of the suggested valuation
procedure with regard to the type of the underlying stochastic
process. On the other hand, the sensitivity of the results
regarding the stochastic process becomes clear: The conver-
sion trigger and investment multiple as well as the options
values of the MRP differ clearly from those of the GBM and
ABM, although the parameter estimation is based on the same
data. This difference can be explained by the respective
process characteristics, which exist with regard to positive
future developments. While prices are fluctuating around
their equilibrium level in an MRP, they can drift freely in the
Brownian motions. That is why the opportunity costs of
immediate conversion are lower for an MRP than for a GBM
and for an ABM. The reasons for the low conversion trigger
price in case of MRP are the relatively high speed of return of
the prices as well as the high equilibrium price level
amounting to 53.4
V t
1
DM which exceeds the cost-covering
constant expected wood chips price of 47.0
V t
1
DM (cf.
Equation
). Thus, a Net Present Value of zero can only arise
from an initial level lower than 47.0
V t
1
DM. The compara-
tively significant effect results from the fact that the wood
chips price will not become relevant for the revenues during
the first four yearsdduring which a low initial value causes
a relatively low expected valuedbut as from the fifth year
after conversion to SRC.
5.
Conclusion and future research
Although numerous studies show that the utilization of agri-
cultural areas for the production of wooden biomass in SRC
might be profitable, only few farmers convert to this cultiva-
tion method. To explain the phenomenon of the observed
reluctance to adapt, different explanatory approaches are
discussed including, for instance, traditionalistic behavior
and risk aversion. However, when assuming that the decision
to convert from a classical agricultural production method to
SRC is an investment decision, a relatively new explanatory
approach gains in importance: Investment decisions are
usually characterized by uncertainty, sunk costs and temporal
flexibility. Taking into account these three aspects, invest-
ment planning takes place within the framework of the Real
Options Approach. Thusdcontrary to the Classical Invest-
ment Theorydthe conversion to SRC can only be recom-
mended if the Net Present Value achieved in case of
immediate conversion compensates at least the opportunity
costs involved at this time, which also include the profitability
of postponing the conversion. In the present study, conver-
sion thresholds and options values are determined for
a model farm at a poor and drought threatened location in
Northern Germany, which has the option to convert a set-
aside agricultural area to SRC. The farmers can postpone the
decision to convert as long as they like. To facilitate the
decision a numerical real options valuation model is devel-
oped. This model is flexible regarding the type of the under-
lying stochastic process.
The results from the examined location illustrate that in
case of realistic assumptions a risk neutral decision-maker
should only convert from set-aside to SRC if the present
value of the revenues is equivalent to 1.57 times the present
value of the expenditures. Hence, there are considerable
differences to the Classical Investment Theory, which
recommends to invest in the event of an investment multiple
of one. Furthermore, the model calculations make clear that
Table 3 e Critical wood chips prices, critical present values of revenues and value of conversion opportunities for different
stochastic processes.
a
Column 1
Column 2
Column 3
Column 4
Column 5
Column 6
Column 7
Column 8
Stochastic
process
Without temporal flexibility (classical
investment theory)
With temporal flexibility (real options
approach)
Investment
multiple
R
=R
M
Critical wood
chips price P
M
(
V t
1
DM)
Critical present
value of the
revenues R
M
(
V ha
1
)
Net Present
Value NPV
0
c
(
V ha
1
)
Critical wood
chips price P*
b
(
V t
1
DM)
Critical present
value of the
revenues R*
(
V ha
1
)
Options
value F
0
c
(
V ha
1
)
1
GBM
47.0
8137
2725
73.6
12,739
4317
1.57
2
ABM
47.0
8137
2725
69.6
12,046
4295
1.48
3
MRP
4.1
8137
1219
40.0
9100
1233
1.12
a With reinvestment option, investment costs of an SRC equal to 2875
V ha
1
, interest rate equal to 3.87% a
1
.
b The parameterization interval of the conversion trigger is refined to up to 0.20
V t
1
DM.
c The Net Present Value and options value have been calculated for an initial wood chips price of P
0
¼ 62.76 V t
1
DM; 50,000 simulation runs.
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
83

the results depend significantly on the type of the stochastic
process underlying the valuation. Besides these normative
statements the results show that the Real Options Approach
indeed has an explanatory potential regarding the frequently
observed reluctance to convert. Of course, it needs to be
checked in further investigations to what extend the results
are specific for the set assumptions of the present study and
how strongly they are influenced by the location conditions,
by the so far applied agricultural production method etc.
From an agricultural and forest policy-makers’ point of
view, the results are relevant as they do not only draw the
attention to the generally known determinants of an invest-
ment decision (e.g. the amount of the investment returns and
their uncertainty or the amount of the costs of conversion) but
also to the temporal flexibility of the investment imple-
mentation under uncertainty. What could policy makers do to
increase the percentage of agricultural area that is used for
SRC, if this is requested? Policy makers, for instance, could pay
additional area payments for SRC, entailing an increase in the
conversion returns. Alternatively, subsidies for cuttings could
be granted. When comparing Net Present Values and options
values it becomes clear that these conversion aids need to be
considerably higher than it might be expected according to the
Classical Investment Theory to have the corresponding effect.
The effect of conversion aids, however, could be amplified if
the payment is limited in time. Ultimately, the opportunity
costs would thereby be reduced over time and the decision to
convert would be shifted more toward a ‘now-or-never-deci-
sion’. Promising more funding of the conversion to SRC for the
future would be the wrong signal. Finally, this would result in
an increase in the intertemporal opportunity costs and
therefore would cause an increased reluctance to convert. Of
course, it is important to point out that interactions between
farms have to be taken into account, if a political intervention
aims to be sustainable.
Acknowledgments
The author would like to thank the editor and anonymous
reviewers for their valuable comments and suggestions. We
gratefully acknowledge financial support from German
Research Foundation (DFG) as well as the German Federal
Ministry of Education and Research (BMBF). Finally, the author
wishes to thank Jessica Olbrich for language assistance.
r e f e r e n c e s
[1] Pallast G, Breuer T, Holm-Mu¨ller K. Schnellwachsende
Baumarten e Chance fu¨r zusa¨tzliches Einkommen im
la¨ndlichen Raum? Ber Landwirtsch 2006;84(1):144e59.
[2] Mu¨hlhausen C. Kein Buch mehr mit sieben Siegeln. Land &
Forst 2010;14(10):64e5.
[3] Aylott MJ, Casella E, Tubby I, Street NR, Smith P, Taylor G.
Yield and spatial supply of bioenergy poplar and willow
short-rotation coppice in the UK. New Phytol 2008;17(2):
358e70.
[4] Ro¨sch C, Skarka J, Raab K, Stelzer V. Energy production from
Grassland e assessing the sustainability of different process
chains under German conditions. JBB 2009;33(4):689e700.
[5] FNR (Fachagentur Nachwachsende Rohstoffe e.V.).
Bioenergy e plants, raw materials, products [Internet].
2nd ed. Hu¨rth: Media Cologne Kommunikationsmedien,
2009. [cited 2011 Oct 27]. Available from:
server.de/ftp/pdf/literatur/pdf_330-bioenergy_2009.pdf
[6] Stolte H. Energieholz und Agroforstsysteme e
Forschungsfo¨rderung durch die FNR e.V.[Internet].
Fachagentur Nachwachsende Rohstoffe e.V. [cited 2011 Oct
27]. Available from:
http://www.tll.de/ainfo/pdf/afs/afs04_
.
[7] Heaton RJ, Randerson PF, Slater FM. The economics of
growing short rotation coppice in the uplands of Mid-Wales
and an economic comparison with Sheep production. JBB
1999;17(1):59e71.
[8] Bemmann A, Feger KH, Gerold D, Grosse W, Hartmann KU,
Petzold R, et al. Kurzumtriebsplantagen auf
landwirtschaftlichen Fla¨chen in der Region Grossenhain im
Freistaat Sachsen. Archive For Sci 2007;78:95e101.
[9] Toews T. Wald e Fla¨chennutzungsanspru¨che durch die
Landwirtschaft. vTI Agric For Res Spec Issue 2009;327:123e30.
[10] Wagner P, Heinrich J, Kro¨ber M, Schweinle J, Grosse W.
O
¨ konomische Bewertung von Kurzumtriebsplantagen und
Einordnung der Holzerzeugung in die Anbaustruktur
landwirtschaftlicher Unternehmen. In: Reeg T, Bemmann A,
Konold W, Murach D, Spiecker H, editors. Anbau und
Nutzung von Ba¨umen auf landwirtschaftlichen Fla¨chen.
Weinheim: WILEY-VCH Verlag; 2009. p. 135e45.
[11] Styles D, Thorne F, Jones MB. Energy crops in Ireland: an
economic comparison of Willow and Miscanthus production
with conventional farming systems. JBB 2008;32(5):407e21.
[12] Dixit AK, Pindyck RS. Investment under uncertainty.
Princeton: Princeton University Press; 1994.
[13] Pietola KS, Wang HH. The value of price and quantity fixing
contracts. Eur Rev Agric Econ 2000;27(4):431e47.
[14] Odening M, Musshoff O, Balmann A. Investment decisions in
hog finishing: an application of the real options approach.
Agr Econ 2005;32(1):47e60.
[15] Kuminoff NV, Wossink A. Valuing the option to convert from
conventional to organic farming. In: AAEA (American
Agricultural Economics Association). Annual Meeting; July
24-27 2005; Providence. USA; Milwaukee: USA.
[16] Musshoff O, Hirschauer N. Adoption of organic farming in
Germany and Austria - an integrative dynamic investment
perspective. Agr Econ 2008;39(1):135e45.
[17] Behan J, McQuinn K, Roche MJ. Rural land use: traditional
agriculture or forestry? Land Econ 2006;82(1):112e23.
[18] Wiemers E, Behan J. Farm forestry investment in Ireland
under uncertainty. Econ Soc Rev 2004;35(3):305e20.
[19] Plantinga AJ. The optimal timber rotation: an option value
approach. Forest Sci 1998;44(2):192e202.
[20] Gjolberg O, Guttormsen AG. Real options in the forest: what if
prices are mean-reverting? Forest Policy Econ 2002;4(1):13e20.
[21] Insley MA. Real options approach to the valuation of
a forestry investment. J Environ Econ Manag 2002;44(3):
471e92.
[22] Trigeorgis L. Real options. Cambridge: MIT-Press; 1996.
[23] McDonald R, Siegel D. The value of waiting to invest. Q J Econ
1986;101(4):707e28.
[24] Hull JC. Options, futures, and other derivatives. 7th ed. Upper
Saddle River: Prentice-Hall; 2009.
[25] Ibanez A, Zapatero F. Monte Carlo valuation of American
options through computation of the optimal exercise
frontier. Financ Quant Anal 2004;39(2):253e75.
[26] Luenberger DG. Investment science. New York: Oxford
University Press; 1998.
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
84

[27] Council Regulation (EC) No 73/2009. Establishing common
rules for direct support schemes for farmers under the
common agricultural policy and establishing certain
support schemes for farmers, amending regulations (EC)
No 1290/2005, (EC) No 247/2006, (EC) No 378/2007 and (EC)
No 1782/2003. 2009.01.19. Official J Eur Union 2009;L 30:
16e99.
[28] Kuratorium fu¨r Technik und Bauwesen in der
Landwirtschaft (KTBL). Betriebsplanung Landwirtschaft
2008/09. Reinheim: Lokay; 2008.
[29] Schattenberg G. Schnell Holz ernten. Bauernzeitung 2010;
10(10):50e2.
[30] Ro¨hle H, Hartmann KU, Steinke C, Murach D.
Leistungsvermo¨gen und Leistungserfassung von
Kurzumtriebsbesta¨nden. In: Reeg T, Bemmann A, Konold W,
Murach D, Spiecker H, editors. Anbau und Nutzung von
Ba¨umen auf landwirtschaftlichen Fla¨chen. Weinheim:
WILEY-VCH Verlag; 2009. p. 41e55.
[31] Biertu¨pfel A, Rudel H, Werner A, Vetter A. 15 Jahre
Energieholzversuche in Thu¨ringen. Report. Jena: Thu¨ringer
Landesanstalt fu¨r Landwirtschaft [Internet] 2009 Oct. [cited
2011 Oct 27]. Available from:
.
[32] Stu¨rmer B, Schmid E. Wirtschaftlichkeit von Weide und
Pappel im Kurzumtrieb unter o¨sterreichischen
Verha¨ltnissen. La¨ndlicher Raum [Internet]. 2007. [cited 2011
Oct 27]. Available from:
http://www.laendlicher-raum.at/
[33] Schultze M, Fiedler P, Bra¨kow D. Logistische Bereitstellung
von Agrarholz fu¨r regionale Nutzungen am Beispiel von
Brandenburg. In: Reeg T, Bemmann A, Konold W, Murach D,
Spiecker H, editors. Anbau und Nutzung von Ba¨umen auf
landwirtschaftlichen Fla¨chen. Weinheim: WILEY-VCH
Verlag; 2009. p. 113e24.
[34] Schultze M. Holzbrennstoffe e Scheitholz-
Holzhackschnitzel-Holzpellets. information brochure of the
Kompetenzzentrum HessenRohstoffe (HeRo) e.V; 2009.
[35] C.A.R.M.E.N. e.V. Preisentwicklung bei Waldhackschnitzeln.
[Internet]. Meissen: Centrales Agrar-Rohstoff-Marketing-
und Entwicklungs-Netzwerk e.V. [cited 2011 Oct 27].
Available from:
http://www.carmen-ev.de/dt/energie/
hackschnitzel/hackschnitzelpreis_jahresmittelwerte.html
.
[36] Kahnt-Ralle E. Erster Energiewald wurde geerntet. Land &
Forst [Internet]. 2010 [cited 2011 Oct 27]; 163(6):42. Available
from:
http://www.landundforst.de/?redid
[37] Hawliczek I. Verbraucherpreise fu¨r Kraftstoffe und Heizo¨l
von 1970 bis 2000. Statistische Monatshefte Rheinland-Pfalz
2001;3:50e7.
[38] Institut fu¨r wirtschaftliche O¨lheizung (IWO). Vergleich der
ja¨hrlichen Brennstoffkosten fu¨r Heizo¨l EL und Erdgas
[Internet]. Hamburg: IWO [cited 2010 Oct 27]. Available
from:
http://www.gastarife-online.de/highlights/
gasinformationen/20_zehn_jahresvergleich_erdgas_
deutlich_teurer_als_heizoel.html
; 1995e2004.
[39] Brennstoffhandel. Heizo¨l-Preise 2009: Heizo¨lpreise fallen um
31 % gegenu¨ber dem Jahr 2008 [Internet] [cited 2011 Oct 27].
Available from:
http://www.brennstoffhandel.de/index.php?
¼news&cs_go¼archiv&cs_id¼1629&cs_search¼
; 2010
Jan.
[40] Dickey DA, Fuller WA. Likelihood ratio statistics for
autoregressive time series with a unit root. Econometrica
1981;49(4):1057e72.
[41] Campbell JY, Lo W, MacKinlay C. The Econometrics of
financial markets. New Jersey: Princeton University Press;
1997.
[42] Pindyck RS, Rubinfeld DL. Econometric models and economic
forecasts. 4th ed. Singapore: McGraw-Hill; 1998.
[43] Postali FAS, Picchetti P. Geometric Brownian motion and
structural breaks in oil prices: a quantitative analysis. Energ
Econ 2006;28(4):506e22.
[44] Baker MP, Mayfield ES, Parsons JE. Alternative models of
uncertain commodity prices for use with modern asset
pricing methods. Energ J 1998;19(1):115e48.
[45] Pilipovic D. Energy risk: valuing and managing energy
derivatives. New York: McGraw-Hill; 1998.
[46] Vasicek O. An equilibrium characterization of the term
structure. J Financ Econ 1977;5(2):177e88.
[47] Deutsche Bundesbank [Internet]. Frankfurt am Main:
Deutsche Bundesbank [cited 2011 Oct 4]. Available from:
http://www.bundesbank.de/statistik/statistik_zeitreihen.
php?lang
¼de&open¼&func¼row&tr¼WU3975#comm
[48] Industrie- und Handelskammer Nord Westfalen (IHK).
Inflationsraten 1975 bis 2005 [Internet]. Mu¨nster: IHK [cited
2010 Oct 27]. Available from:
; 2006.
[49] Hudson D, Coble K, Lusk J. Consistency of risk premium
measures. Agr Econ 2005;33(1):41e9.
[50] Gebremedhin TG, Gebrelul S. An investment analysis of meat
goat enterprises for small-scale producers. Rev Agr Econ
1992;14(1):45e53.
[51] Berg E. Modeling the impacts of uncertainty and attitudes
towards risk on production decisions in arable farming. In:
(International Association of agricultural Economists). 25th
International Conference of the IAAE; August 16-22 2003;
Durban, South Africa; Milwaukee:USA.
[52] Marchant MA, Murrell CP, Zhuang J. Investment analysis of
replacing endophyte-infected with endophyte-free tall
fescue pastures. Annual Meeting of the Southern
Agricultural Economics Association; February 14-18 2004;
Tulsa. USA; Lubbock:USA.
[53] Haug EG. The complete guide to option pricing formulas.
New York: McGraw-Hill; 1998.
b i o m a s s a n d b i o e n e r g y 4 1 ( 2 0 1 2 ) 7 3 e8 5
85
Document Outline
- Growing short rotation coppice on agricultural land in Germany: A Real Options Approach
Wyszukiwarka
Podobne podstrony:
Economics of poplar short rotation coppice plantations on marginal land in Germany 2013 Biomass and
Efficient harvest lines for Short Rotation Coppices (SRC) in Agriculture and Agroforestry Niemcy 201
The economics of short rotation coppice in Germany 2012
Economic, energetic and environmental impact in short rotation coppice harvesting operations Włochy
Elemental composition of willow short rotation crops biomass depending on variety and harvest cycle
Elemental composition of willow short rotation crops biomass depending on variety and harvest cycle
Effect of Kinesio taping on muscle strength in athletes
Changes in passive ankle stiffness and its effects on gait function in
Impact of resuscitation system errors on survival from in hospital cardiac arrest
Graeme?rker ''The Agricultural Revolution in Prehistory''
Impact of resuscitation system errors on survival from in-hospital cardiac arrest, MEDYCYNA, RATOWNI
Effect of Kinesio taping on muscle strength in athletes
Changes in passive ankle stiffness and its effects on gait function in
Ava March Gambling On Love 1 All In with the Duke
prepositions of time on at and in 2 brb29
dokument The Cairo Declaration on Human Rights in Islam
The Effect of DNS Delays on Worm Propagation in an IPv6 Internet
więcej podobnych podstron