Dynamics of diesel and wind turbine generators on an isolated power

system

D. Das

a,

*, S.K. Aditya

a

, D.P. Kothari

b

a

Electrical Eng. Dept., Indian Institute of Technology, Kharagpur—721302, India

b

Centre for Energy Studies, Indian Institute of Technology, New Delhi—110016, India

Abstract

The paper presents dynamic system analysis of an isolated electric power system consisting of a diesel generator and a wind turbine

generator. The 150 kW wind turbine generator is operated in parallel with a diesel generator to serve an average load of 350 kW. Time
domain solutions are used to study the performance of the power system. Optimum values of gain settings of the Proportional-Integral
controller (P-I) are obtained by using the integral squared error (ISE) technique. A simple variable structure control (VSC) logic is also
proposed for improvement of the dynamic performance of the system.

䉷 1998 Elsevier Science Ltd. All rights reserved.

Keywords: Wind and diesel power system; Stability; Optimization

1. Introduction

A constantly increasing power demand has to be met

through an adequately planned electrical power generation
programme. Electrical energy is environmentally the most
benign form of energy, with production routed through
conventional fossil fuel burning or through nuclear energy
and wherever possible through hydro resources. All of these
in addition to other disadvantages give rise to environmental
issues of a varied nature. Therefore it is necessary to
consider the problems of electrical energy generation and
environment jointly so that the increasing need of electricity
for industrialization will be met with minimal environmen-
tal degradation. One of the solutions is to utilize wind
energy in favourable sites which are remote from centralised
energy supply systems. Since wind power varies randomly
there must be a stand-by power source to meet load demand.
The diesel and wind system is one of the hybrid systems
utilizing more than one energy source. A wind and diesel
system is very reliable because the diesel acts as a cushion to
take care of variation in wind speed, and would always
provide power equal to load minus the wind power.

Scott et al. [1] have investigated the dynamic interaction

to quantify any increased disturbance to the Block Island
Power Company (BIPCO), on Block Island (which operates
an isolated electric power system consisting of diesel and
wind turbine generators resulting from connection of the
MOD-OA wind turbine generator). In this study, the

dynamic simulation of the wind turbine generator operated
in parallel with a diesel generator on an isolated power
system is carried out. Optimum values for the gain settings
of the Proportional-Integral (P-I) controller have been
obtained using the Integral Squared Error (ISE) technique.
A simple Variable Structure Control (VSC) logic is also
proposed for the improvement of system dynamic perfor-
mance.

2. Description of diesel and wind systems

The model considered in this study consists of the follow-

ing sub-systems [1,3,4]:

Wind dynamics model;
Diesel dynamics model;
Blade pitch control of wind turbine;
Generator dynamics model.

The wind model is one feature that is unique to the wind

turbine generator and is not required for the diesel generator
system in the stability programme. Anderson et al. [2] have
presented one model that can properly simulate the effect of
wind behaviour, including gusting, rapid (ramp) changes
and background noise. The basic conditions for start up
and synchronization are that the wind speed is to be within
an acceptable range and there must be a phase match
between the generator and system voltages [1].

The diesel dynamics is associated with diesel power and

the nature of the dynamic behaviour in this model is

Electrical Power and Energy Systems 21 (1999) 183–189

JEPE 278

0142-0615/99/$ - see front matter

䉷 1998 Elsevier Science Ltd. All rights reserved.

PII: S 0 1 4 2 - 0 6 1 5 ( 9 8 ) 0 0 0 3 3 - 7

* Corresponding author; e-mail: [e-mail].

dominated by the diesel speed governor controller. A total
power set point is selected in which it can manually adjusted
from zero to maximum value. The purpose of the adjustable
power set point is to allow system utility personnel to lower
the power setting below the maximum settings of the wind
generator to prevent controlling diesel from dropping to less
than 50% of the rated power. Operation of a diesel engine
for extended periods at two power levels could result in
possible engine damage.

Pitch control has the potential for producing the highest

level of interaction because of the presence of both diesel
and wind turbine control loops. The pitch control system
consists of a power measurement transducer, a manual
power set point control, a proportional plus integral feed-
back function, and a hydraulic actuator which varies the
pitch of the blades. Turbine blade pitch control has a signif-
icant impact on the dynamic behaviour of the system. This
type of control only exists in horizontal axis machines.

Variable pitch turbines operate efficiently over a wider
range of wind speeds than fixed pitch machines. However,
cost and complexity are higher.

The generator dynamics model consists of a synchronous

generator driven by a diesel engine through a flywheel and
connected in parallel with an induction generator driven by
a wind turbine. The diesel generator will act as a dummy
grid for the wind generator which is connected in parallel.
Variations of electrical power due to changes in wind speed
should be as small as possible; this is obtained by using the
induction generator as a wind turbine drive train. Unlike
synchronous generators, induction generators are high
compliance couplings between the machine and the electri-
cal system. This is true for induction generators with slip of
at least 1–2% at rated power. The controlled variables are
turbine speed and shaft torque. Control acts on the turbine
blade pitch angle (pitch control). Since the torque speed
characteristic of the induction generator is nearly linear in

D. Das et al. / Electrical Power and Energy Systems 21 (1999) 183–189

184

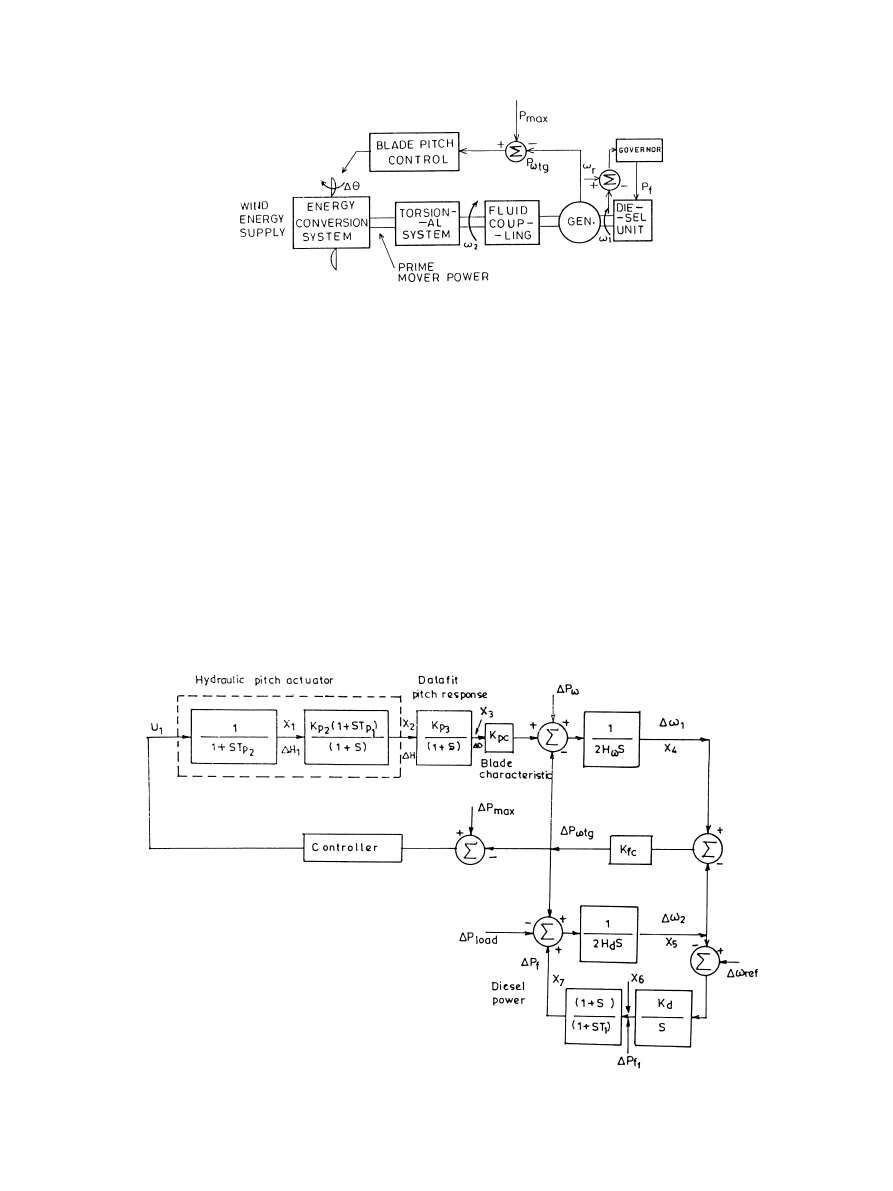
Fig. 1. Conceptual model of diesel and wind turbine generator system.

Fig. 2. Functional block diagram for wind and diesel systems with pitch control.

the operating region, torque changes are reflected as speed
changes. Therefore, it is possible to provide a single speed
controller to control speed as well as torque.

3. Mathematical model of the system

A linear model is formulated for the wind and diesel

turbine generator system for the purpose of identifying
and quantifying the underdamped oscillation. This objective
is met by retaining the pertinent controller dynamics for
both the diesel unit governors and wind turbine generator
pitch controller/actuator. The conceptual model that results
is shown in Fig. 1. The fluid coupling shown in Fig. 1
transfers speed difference into power. The actual function
is nonlinear (Square law) but for the model it is linearized,
resulting in a constant for the particular power set point
selected. Fig. 2 shows the functional block diagram that is
obtained.

The transfer function of the hydraulic pitch actuator is

given as:

DH…S†

U

1

…S†

ˆ

K

p2

…1 ⫹ ST

p1

†

…T

k

S

2

⫹ ST

p2

⫹ 1†…1 ⫹ S†

…1†

But T

k

is very small compared to T

p2

and hence T

k

is

neglected from the mathematical model. Therefore Eq. (1)
can be written as

DH…S†

U

1

…S†

ˆ

K

p2

…1 ⫹ ST

p1

†

…1 ⫹ ST

p2

†…1 ⫹ S†

…2†

The transfer function Eq. (2) of the hydraulic pitch actua-

tor is split into two blocks (Fig. 2) and

DH

1

is a dummy

variable.

The transfer function of the diesel governor (Fig. 2) is

given as:

DP

f

…S†

D

v

ref

…S† ⫺ D

v

2

…S†

ˆ

K

d

…1 ⫹ S†

S

…1 ⫹ ST

1

†

…3†

As

v

ref

is the reference speed setting (a constant) for the

diesel generator, therefore

Dv

ref

ˆ 0.0. Substituting Dv

ref

ˆ

0.0 in Eq. (3), we get

DP

f

…S†

⫺ D

v

2

…S†

ˆ

K

d

…1 ⫹ S†

S

…1 ⫹ ST

1

†

…4†

The transfer function of the diesel governor Eq. (4) is split

into two blocks and

DP

f1

is a dummy variable.

Appearing in a block (Fig. 2) labelled ‘data fit pitch

response’ is a simple lag which is required to match the
phase/gain characteristic of the model. Other state variables
are marked in Fig. 2. The system is a linear continuous-time
dynamic system and can be represented by a set of linear
differential equations of the form:

_X ˆ AX ⫹ BU ⫹ GP

…5†

where X, U and P are state, control and disturbance vectors
and A, B and

G are constant matrices associated with them

respectively. For this system (Fig. 2), X, U and P are
given as

X

0

ˆ ‰DH

1

DH DD D

v

1

D

v

2

DP

f 1

DP

f

Š

…6†

U

ˆ U

1

…7†

P

0

ˆ ‰DP

v

DP

load

Š

…8†

where,

0

stands for transpose. A, B and

G are given in

Appendix

1.

Data

for

this

system

are

given

in

Appendix 2.

D. Das et al. / Electrical Power and Energy Systems 21 (1999) 183–189

185

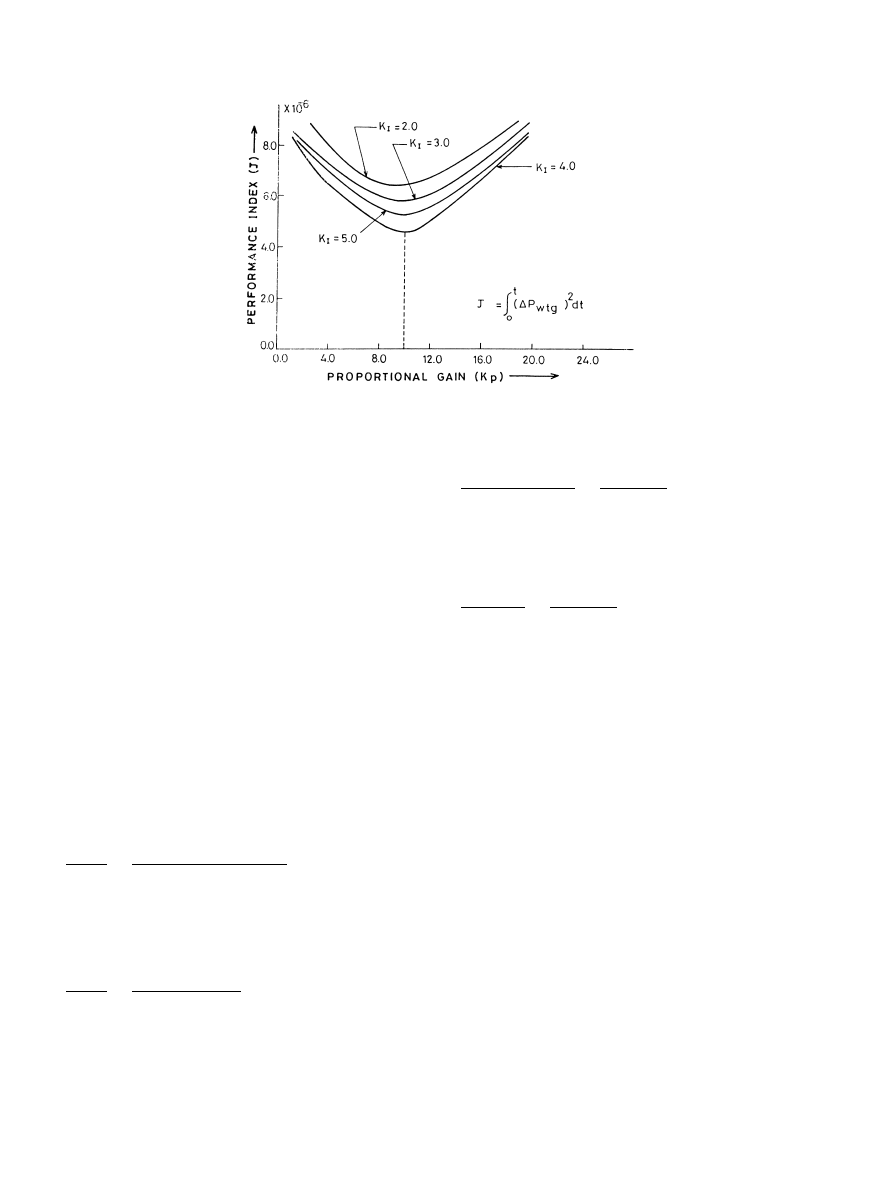
Fig. 3. K

p

vs J for several values of K

I

.

4. Optimization of the Proportional-Integral (P-I)
controller gain settings using the ISE technique

Many utilities prefer to use the P-I controller for

better system dynamic response and in the present
study, the P-I controller is used. The P-I control law

is given as

U

1

ˆ K

p

…DP

max

⫺ DP

vtg

† ⫹ K

I

Z

t

0

…DP

max

⫺ DP

vtg

† dt …9†

For the study system, P

max

ˆ 150 kW is constant, there-

fore

DP

max

ˆ 0.0. Substituting DP

max

ˆ 0.0 in Eq. (9)

we obtain

U

1

ˆ ⫺K

p

…DP

vtg

† ⫺ K

I

Z

t

0

DP

vtg

dt

…10†

An attempt is made to obtain the optimum values of P-I
gain settings (K

p

and K

I

) using the integral squared error

(ISE) technique for a 1% step increase of load.

A performance index

J

ˆ

Z

t

0

…DP

vtg

†

2

dt

…11†

is minimized to obtain the optimum values for P-I gain
settings. Note that

DP

vtg

is also a function of

Dv

1

and

Dv

2

(Fig. 2).

Fig. 3 shows the plot of J vs K

p

for several values of

K

I

, where K

p

and K

I

are proportional and integral gains

D. Das et al. / Electrical Power and Energy Systems 21 (1999) 183–189

186

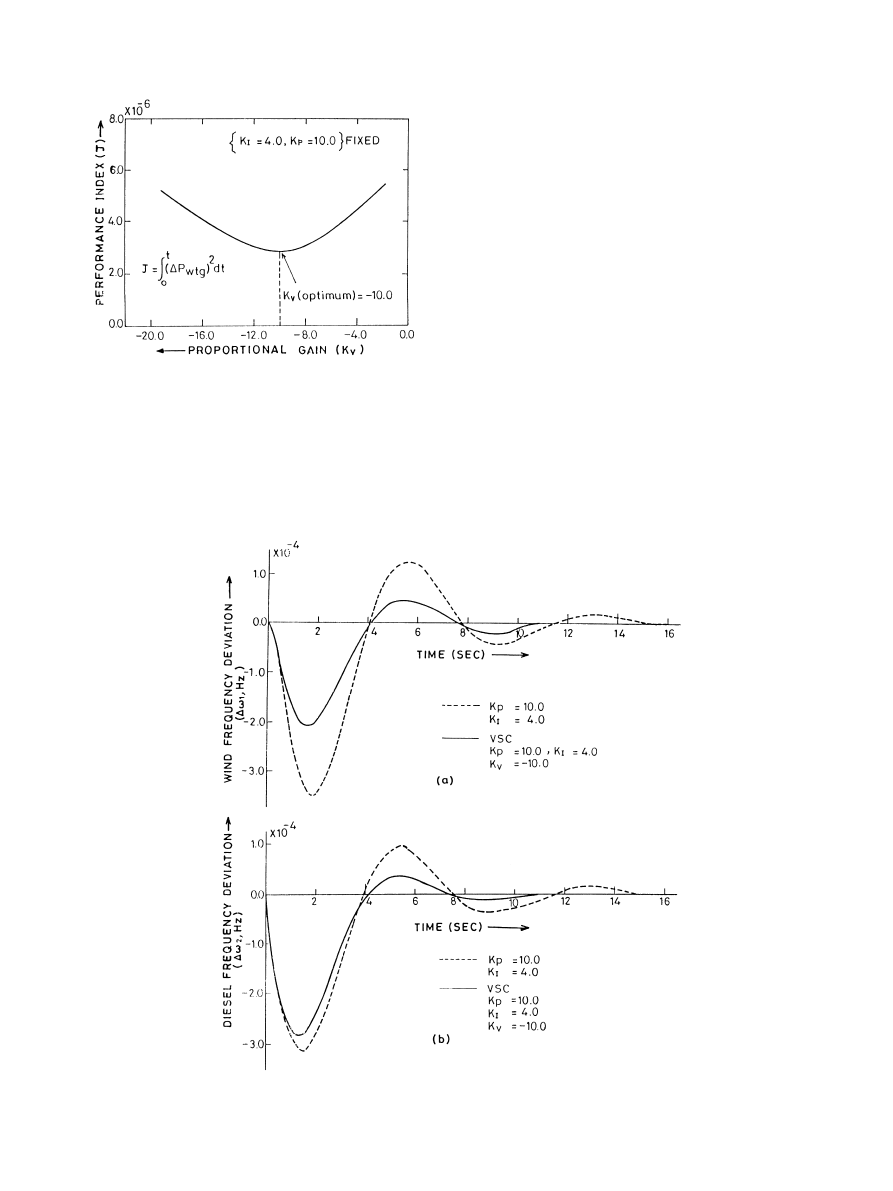
Fig. 4. Plot of K

v

vs J.

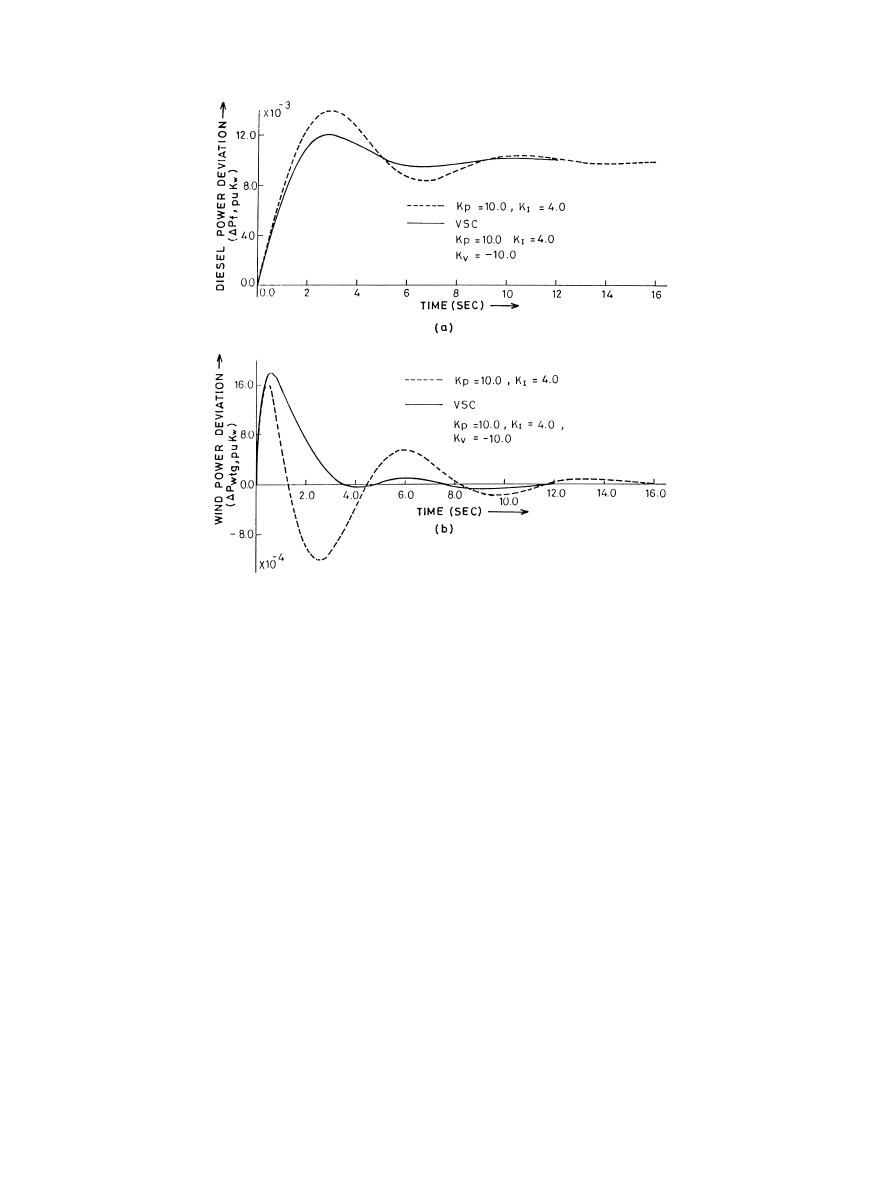
Fig. 5. Frequency responses with conventional and variable structure controllers.

respectively. From Fig. 3, it is seen that K

p

ˆ 10:0 and K

I

ˆ

4

:0 are more or less optimum values of P-I gain settings.

5. Variable structure control (VSC) logic

In this study, an attempt is also made to improve the

system dynamic performance by using a simple variable
structure control (VSC) logic which is based on proportional
(P) and proportional-integral (P-I) control concept. If the
control law applied at the first stage of the transient (as
long as error is sufficiently large) is chosen as

U

1

ˆ ⫺K

v

DP

vtg

if

兩DP

vtg

兩典

1

…12†

where

1

⬎ 0 is some constant, but when the error is small

the control law is

U

1

ˆ ⫺K

p

DP

vtg

⫺ K

I

Z

t

0

DP

vtg

dt if

兩DP

vtg

兩 ⱕ

1

…13†

where

兩DP

vtg

兩典

1

for t

ⱖ t

1

, then if the parameters K

v

, K

p

, K

I

and

1 are suitably selected, one can ensure a high-quality

transient response, distinguished by good dynamic and
steady-state characteristics. Indeed taking the magnitude
of K

v

as being sufficiently large, one can make sure that

the speed of the system is high; thus, the error

DP

vtg

, in

response to a step input rapidly enters the region
兩DP

vtg

兩 ⱕ

1

. At the instant t

1

, when the error has fallen to

1, the structure of the controller is changed by switching to a
P-I control, which eliminates the steady error remaining in
the system.

An attempt is made to obtain optimum values of K

v

by

using the ISE technique. The same performance index J Eq.
(11) is chosen to obtain the optimum values of K

v

. Through-

out this optimization process, values of K

p

and K

I

are fixed at

10.0 and 4.0, respectively. Fig. 4 shows the plot of J vs K

v

for

1 ˆ 0.0004. It is worth mentioning here that several

values of

1 are tried out. However, 1 ˆ 0.0004 gives the

lowest value of J. From Fig. 4, it is seen that the optimum
value of K

v

is

⫺ 10.0. However, any positive value of K

v

does not minimize the performance index J Eq. (11) and
perhaps this is due to excessive control action.

6. Dynamic responses

Figs. 5 and 6 show the dynamic responses for a 1% step

increase of load with the P-I controller and variable struc-
ture controller (VSC). It is seen that the activation of pitch
control with the conventional P-I controller results in an
underdamped response. Although this is a stable response,
the low damping allows the oscillation to continue for a

D. Das et al. / Electrical Power and Energy Systems 21 (1999) 183–189

187

Fig. 6. Power responses with conventional and variable structure controllers.

longer time before damping out. It is seen that with the use
of VSC, damping is greatly improved. Peak wind generator
frequency deviation (Fig. 5(a)) and peak diesel power devia-
tion (Fig. 6(a)) are much less compared to the conventional
P-I controller. From Fig. 6(b), it is also seen that with the use
of VSC, the wind power deviation (

DP

vtg

) is slow and

monotonic and hence is preferred. From Figs 5 and 6, it is
also seen that with the use of VSC, settling time is much less
compared to that of the conventional P-I controller. There-
fore, it can be concluded that the variable structure control-
ler improves the system damping compared to the fixed
structure P-I controller.

7. Conclusions

A linear mathematical model of the wind and diesel turbine

generators operating on an isolated electric power system has
been formulated for the purpose of identifying and quantifying
the underdamped oscillation. The simulation incorporates
wind turbine pitch control and diesel governor. Optimum
values for the gain parameters of the conventional propor-
tional-integral (P-I) controller and variable structure controller
(VSC) have been obtained using the integral squared error
(ISE) technique. Analysis reveals that the variable structure
controller gives better dynamic performance in terms of peak

deviations and settling time compared to that of the conven-
tional fixed structure P-I controller.

It can also be concluded that wind turbine generation,

even when providing a large proportion of the power
required by an isolated utility can be a practical option
resulting in system disturbances no greater than those
found in a conventional diesel system.

Appendix 1

A, B and

G matrices of the system (Fig. 2) are given

below:

Note that B is a 7

× 1 matrix because there is only one

control input.

Appendix 2

Area capacity

; P

R

ˆ 350 kW;

H

v

ˆ inertia constant on machine base ˆ

3

:5 s for wind system;

H

d

ˆ inertia constant on machine base ˆ

8

:5 s for diesel system;

D. Das et al. / Electrical Power and Energy Systems 21 (1999) 183–189

188

A

ˆ

⫺1
T

p2

0

0

0

0

0

0

K

p2

⫺

K

p2

T

p1

T

p2

!

⫺1

0

0

0

0

0

0

K

p3

⫺1

0

0

0

0

0

0

K

pc

2H

v

⫺K

fc

2H

v

K

fc

2H

v

0

0

0

0

0

K

fc

2H

d

⫺K

fc

0

1

0

0

0

0

⫺K

d

0

0

0

0

0

0

⫺K

d

T

1

1

T

1

⫺1

T

1

2
6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

4

3
7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

5

B

ˆ

1

T

p2

K

p2

T

p1

T

p2

0

0

0

0

0

2
6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

4

3
7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

5

; G ˆ

0

0

0

0

0

0

1

2H

v

0

0

⫺1

2H

d

0

0

0

0

2
6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

6

4

3
7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

7

5

K

fc

ˆ 16:2 pu kW=Hz K

d

ˆ 16:5 pu kW=Hz;

K

p2

ˆ 1:25

T

p2

ˆ 0:041 s;

K

p3

ˆ 1:40

T

p1

ˆ 0:60 s;

DP

load

ˆ 0:01 pu kW K

pc

ˆ 0:80;

T

1

ˆ 0:025 s

T

k

ˆ 0:0009 s:

References

[1] Scott GW, Wilrekar VF, Shaltens RK. Wind turbine generator interac-

tion with diesel generators on an isolated power system. IEEE Trans
Power Apparatus Syst 1984;PAS 103(5):933–937.

[2] Anderson PM, Bose A. Stability simulation of wind turbine systems.

IEEE Trans Power Apparatus Syst 1983;PAS 102(12):3791–3795.

[3] Hinrichsen EN. Controls for variable pitch wind turbine generators.

IEEE Trans Power Apparatus Syst 1984;PAS 103(4):886–892.

[4] Hinrichsen EN, Nolan PJ. Dynamics and stability of wind turbine

generators.

IEEE

Trans

Power

Apparatus

Syst

1982;PAS

101(8):2640–2648.

D. Das et al. / Electrical Power and Energy Systems 21 (1999) 183–189

189