Power Converters and Control of Renewable Energy Systems

Marco Liserre

Politecnico di Bari, DEE

Italy

[e-mail]

Frede Blaabjerg, Remus Teodorescu, Zhe Chen

Aalborg University, Institute of Energy Technology,

Denmark

[e-mail], [e-mail], [e-mail]

Abstract — The global electrical energy consumption is steadily
rising and therefore a continous demand to increase the power
generation capacity. A significant percentage of the required
capacity increase can be based on renewable energy sources.
Wind turbine technology, as the most cost effective renewable
energy conversion system, will play an important part in our
future energy supply. But other sources like microturbines,
photovoltaics and fuel cell systems may also be serious
contributors to the power supply. Characteristically, power
electronics will be an efficient and important interface to the
grid for the renewables and this paper will first briefly discuss
three different alternative/renewable energy sources. Next,
various configurations of small and medium power conversion
topologies are presented including their control (mainly for
PV-systems). Finally wind turbine configuration and their
control are described.

I.

I

NTRODUCTION

The energy consumption is steadily increasing and the

deregulation of electricity has caused that the amount of
installed production capacity of classical large power
stations cannot follow the demand. A method to fill out the
gap is to make incentives to invest in alternative energy
sources like wind turbines, photovoltaic systems,
microturbines and also fuel cell systems. Two renewable
energy systems are the most dominant so far which are the
wind turbines and the photovoltaic systems. The wind
turbine technology is one of the most promising alternative
energy technology [1]-[3]. The modern development started
in the 1980’s with sites of a few tens of kW to Multi-MW
range wind turbines today. E.g. Denmark has a high
penetration (> 20%) of wind energy in major areas of the
country and in 2003 15% of the whole electrical energy
consumption was covered by wind energy. A higher
penetration level will even be seen in the near future. As the
power range of the wind turbines increases the key
parameters like control of active and reactive power become
more and more important. The power electronics is the key-
technology [4]-[5]to change the basic characteristic of the
wind turbine from being an energy source to be an active
power source [6]-[36]. The power electronic possibilities are
also used to interface other renewable energy sources [37]-
[46].

This paper will first explain the basic principles of wind

power conversion, fuel cells and photovoltaic. Next different
PV configurations are explained as well as power converters
and their control. The three-phase inter-connection is also
discussed including control. Different wind turbine
configurations are finally reviewed together with their
control methods.

II.

R

ENEWABLE

E

NERGY

S

OURCES

Three different renewable energy sources are briefly

described. They are wind power, fuel cell and photovoltaic.

A. Wind power conversion

The function of a wind turbine is to convert the motion of

the wind into rotational energy that can be used to drive a
generator, as illustrated in Fig. 1. Wind turbines capture the
power from the wind by means of aerodynamically designed
blades and convert it into rotating mechanical power. At
present, the most popular wind turbine is the Horizontal
Axis Wind Turbine (HAWTs) where the number of blades is
typically three.

Wind turbine blades use airfoils to develop mechanical

power. The cross-sections of wind turbine blades have the
shape of airfoils as the one shown in Fig. 2.

Airflow over an airfoil produces a distribution of forces

along the airfoil surface. The resultant of all these pressure
and friction forces is usually resolved into two forces and a
moment, lift force, drag force and pitching moment, as
shown in Fig. 2.

The aerodynamic power, P, of a wind turbine is given by:

p

C

v

R

P

3

2

2

1

ρπ

=

(1)

where

ρ is the air density, R is the turbine radius, v is the

wind speed and C

P

is the turbine power coefficient which

represents the power conversion efficiency of a wind turbine.
C

P

is a function of the tip-speed ratio (

λ), as well as the

blade pitch angle (

β) in a pitch controlled wind turbine. λ is

defined as the ratio of the tip speed of the turbine blades to
wind speed, and given by:

v

R

Ω

⋅

=

λ

(2)

where

Ω is the rotational speed of the wind turbine.

The Betz limit, C

P,max (theoretical)

=16/27, is the maximum

theoretically possible rotor power coefficient. In practice
three effects lead to a decrease in the maximum achievable
power coefficient [1]:

•

Rotation of the wake behind the rotor

•

Finite number of blades and associated tip losses

•

Non-zero aerodynamic drag

W

A typical C

P

-

λ curve for a fixed pitch angle β is shown in

Fig. 3. It can be seen that there is a practical maximum
power coefficient, C

P,max

. Normally, a variable speed wind

turbine follows the C

P,max

to capture the maximum power up

to the rated speed by varying the rotor speed to keep the
system at the optimum tip-speed ratio,

λ

opt

.

As the blade tip-speed typically should be lower than half

the speed of sound the rotational speed will decrease as the
radius of the blade increases. For MW wind turbines the
rotational speed will be 10-15 rpm. A common way to
convert the low-speed, high-torque power to electrical
power is to use a gear-box and a normal speed generator as
illustrated in Fig. 1. The gear-box is optional as multi-pole
generator systems are alternative solutions.

Fig. 2. A simple airfoil used in wind turbines.

Fig. 3. Typical Cp-

λ curve for a wind turbine for a fixed angle β.

The development in the wind turbine systems has been

steady for the last 25 years and four to five generations of
wind turbines exist. It is now a proven technology.

It is important to be able to control and limit the power at

higher wind speeds, as the power in the wind is a cube of the
wind speed.

Wind turbines have to be cut out at a high wind speed to

avoid damage. A turbine could be designed in such a way
that it converts as much power as possible in all wind speeds,
but then it would have to be too heavy. The high costs of
such a design would not be compensated by the extra
production at high winds, since such winds are rare.
Therefore, turbines usually reach maximum power at a
much lower wind speed, the rated wind speed (9-12 m/s).

The power limitation may be done by one of the

aerodynamic mechanisms: stall control (the blade position is
fixed but stall of the wind appears along the blade at higher
wind speed), active stall (the blade angle is adjusted in order
to create stall along the blades) or pitch control (the blades
are turned out of the wind at higher wind speed).

B. Fuel Cell power conversion

The fuel cell is a chemical device, which produces

electricity directly without any intermediate stage and has
recently received much attention [7]. The most significant
advantages are low emission of green house gases and high
power density. For example, a zero emission can be
achieved with hydrogen fuel. The emission consists of only
harmless gases and water. The noise emission is also low.
The energy density of a typical fuel cell is 200 Wh/l, which
is nearly ten times of a battery. Various fuel cells are
available for industrial use or currently being investigated
for use in industry, including

• Proton Exchange Membrane

• Solid Oxide

• Molten Carbonate

• Phosphoric Acid

• Aqueous Alkaline

The efficiency of the fuel cell is quite high (40%-60%). Also

the waste heat generated by the fuel cell can usually be used
for cogeneration such as steam, air-conditioning, hot air and
heating, then the overall efficiency of such a system can be
as high as 80%.

Angle of attack:

Trailing edge

wind

Leading edge

Lift force

Drag force

Pitching moment

α

α

β

β

φ

Pitch angle:

Fig. 1. Conversion from wind power to electrical power in a

e [11].

po

l

wind turbin

Fig. 1. Conversion from wind power to electrical power in a wind turbine [11].

Power conversion &

wer contro

ind power

Power converter

(optional)

Power conversion &

power control

Power conversion

Power transmission

Power transmission

Supply grid

Consumer

Rotor

Gearbox (optional)

Generator

Electrical Power

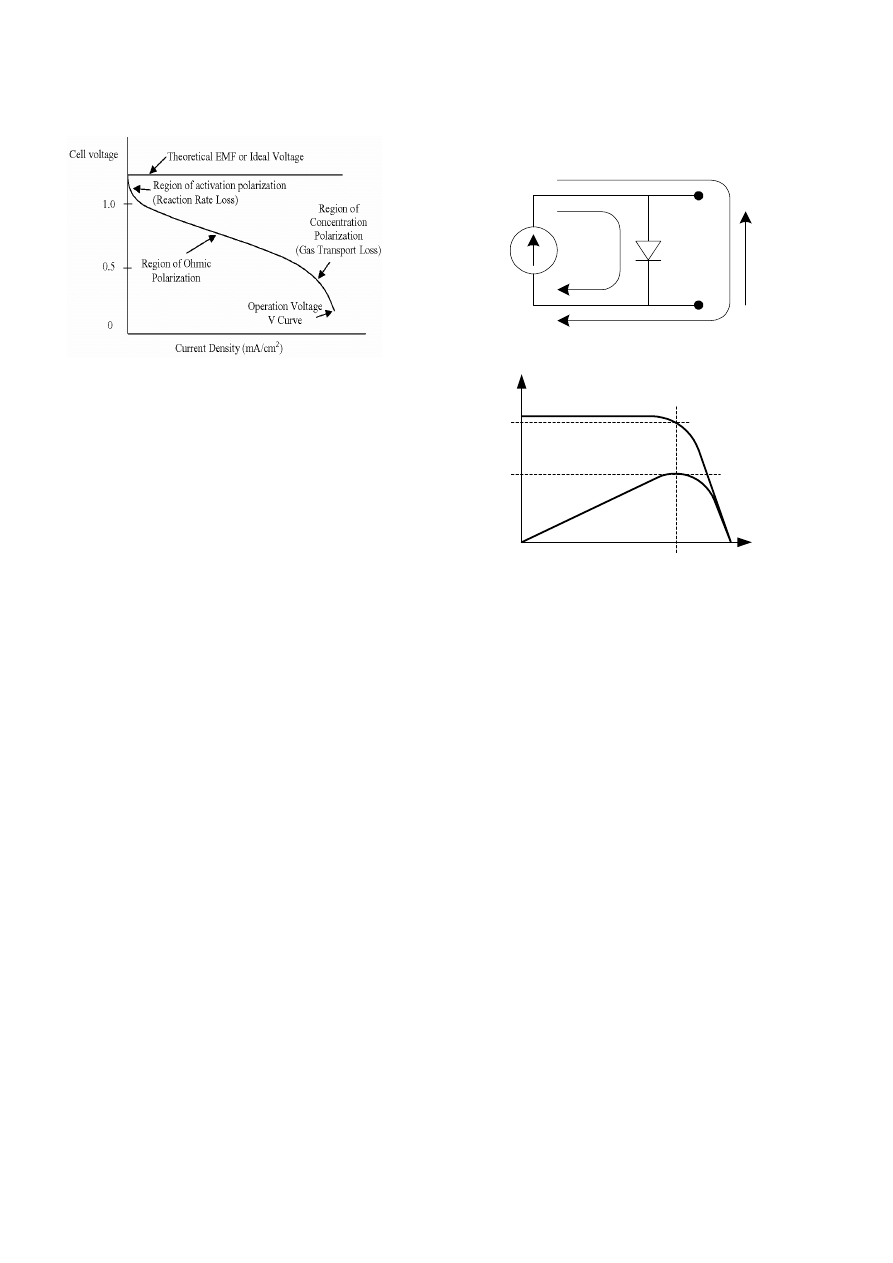
Fig. 4. V-I characteristics of a fuel cell [12].

A typical curve of the cell electrical voltage against current

density is shown in Fig. 4. It can be seen that there exists a
region where the voltage drop is linearly related with the
current density due to the Ohmic contact.

Beyond this region the change in output voltage varies

rapidly. At very high current density, the voltage drops
significantly because of the gas exchange efficiency. At low
current level, the Ohmic loss becomes less significant, the
increase in output voltage is mainly due to the activity of the
chemicals. Although the voltage of a fuel cell is usually
small, with a theoretical maximum being around 1.2 V, fuel
cells may be connected in parallel and/or in series to obtain
the required power and voltage.

The power conditioning systems, including inverters and

DC/DC converters, are often required in order to supply
normal customer load demand or send electricity into the
grid.

C. The photovoltaic cell

Photovoltaic (PV) power supplied to the utility grid is

gaining more and more visibility due to many national
incentives [7]. With a continuous reduction in system cost
(PV modules, DC/AC inverters, cables, fittings and man-
power), the PV technology has the potential to become one
of the main renewable energy sources for the future
electricity supply.

The PV cell is an all-electrical device, which produces

electrical power when exposed to sunlight and connected to
a suitable load. Without any moving parts inside the PV
module, the tear-and-wear is very low. Thus, lifetimes of
more than 25 years for modules are easily reached. However,
the power generation capability may be reduced to 75% ~
80% of nominal value due to ageing. A typical PV module is
made up around 36 or 72 cells connected in series,
encapsulated in a structure made of e.g. aluminum and tedlar.
An electrical model of the PV cell is depicted in Fig. 5.

i

SC

i

PV

i

d

u

PV

(a)

I

PV

P

PV

p

MPP

U

PV

u

OC

i

SC

(u

MPP

, i

MPP

)

(b)

Fig. 5. Model and characteristics of a PhotoVoltaic (PV) cell.

(a) Electrical model with current and voltages defined.
(b) Electrical characteristic of the PV cell, exposed to a given amount

of sunlight at a given temperature.

Several types of proven PV technologies exist, where the
crystalline (PV module light-to-electricity efficiency:

η =

10% - 15%) and multi-crystalline (

η = 9% - 12%) silicon

cells are based on standard microelectronic manufacturing
processes. Other types are: thin-film amorphous silicon (

η =

10%), thin-film copper indium diselenide (

η = 12%), and

thin-film cadmium telluride (

η = 9%). Novel technologies

such as the thin-layer silicon (

η = 8%) and the dye-sensitised

nano-structured materials (

η = 9%) are in their early

development. The reason to maintain a high level of
research and development within these technologies is to
decrease the cost of the PV-cells, perhaps on the expense of
a somewhat lower efficiency. This is mainly due to the fact
that cells based on today’s microelectronic processes are
rather costly, when compared to other renewable energy
sources.
The series connection of the cells benefit from a high
voltage (around 25 V ~ 45 V) across the terminals, but the
weakest cell determines the current seen at the terminals.

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0

6

Cell voltage [V]

15

o

C

40

o

C

75

o

C

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0

0.5

1

1.5

2

2.5

Cell voltage [V]

15

o

C

40

o

C

75

o

C

1000 W/m

2

600 W/m

2

200 W /m

2

(a)

(b)

4

2

Cell

c

u

rrent [A

]

C

e

ll power

[W

]

Fig. 6. Characteristics of a PV cell. Model based on the British Petroleum
BP5170 crystalline silicon PV module. Power at standard test condition
(1000 W/m

2

irradiation, and a cell temperature of 25

°C): 170 W @ 36.0 V.

Legend: solid at 15

o

C, dotted at 40

o

C, and dashdot at 75

o

C [7].

This causes reduction in the available power, which to
some extent can be mitigated by the use of bypass diodes, in
parallel with the cells. The parallel connection of the cells
solves the ‘weakest-link’ problem, but the voltage seen at
the terminals is rather low. Typical curves of a PV cell
current-voltage and power-voltage characteristics are plotted
in Fig. 6a and Fig. 6b respectively, with insolation and cell
temperature as parameters. The graph reveals that the
captured power is determined by the loading conditions
(terminal voltage and current). This leads to a few basic
requirements for the power electronics used to interface the
PV module(s) to the utility grid.

The job for the power electronics in renewable energy

systems is to convert the energy from one stage into another
stage to the grid (alternative voltage) with the highest
possible efficiency, the lowest cost and to keep a superior
performance. The basic interfacing is shown in Fig. 7.
Usually the power converter interfacing a dc source to the
load and/or to the grid consists of a two stage converter: a
standard buck inverter and an ac/ac voltage amplifier or a dc
boost converter [7]. The use of current source inverters is
quite limited because they require several devices producing
a large amount of conduction losses, sluggish transient
response and high cost [66]. An interesting alternative
solution could be the use of a step-up inverter made by the
connection of two [67] or three [68] dc/dc boost converters
in order for the inverter and boost the voltage in only one
stage.
This power electronic system can be used with many
different loads and generators. In this case focus will be on
PV and wind turbines.

Power converter

Reference (local/centralized)

Control

Power flow

Load /

generator

Loads
Appliance
Industry
Communication

Generators
Wind
Photo-voltaic
Fuel cell
Other sources

2-3

2-3

Fig. 7. Power electronic system with the grid, load/source, power

converter and control.

III.

S

INGLE

-

PHASE

PV-

INVERTERS

The first systems to be discussed will be single-phase
connected PV inverters. The general block diagram of a
single-phase grid connected photovoltaic systems is shown
in Fig. 8a. It consists of a PV array, a PV inverter with a
filter, a controller and the grid.

PV

Array

PV Inverter

& Filter

Grid

Control

reference

a)

(b) (c) (d)

Fig 8. General schema for single-phase grid connected photovoltaic

systems. a) Block diagramof PV inverter;

b) Central inverter; c) String

inverter; d) Module integrated inverter

The PV array can be a single panel, a string of PV panels
or a multitude of parallel strings of PV panels. Centralized
or decentralized PV systems can be used as depicted in Fig.
8b - Fig. 8d.

Central inverters
In this topology the PV plant (typical > 10 kW) is arranged
in many parallel strings that are connected to a single central
inverter on the DC-side (Fig. 8b). These inverters are
characterized by high efficiency and low specific cost.
However, the energy yield of the PV plant decreases due to
module mismatching and potential partial shading

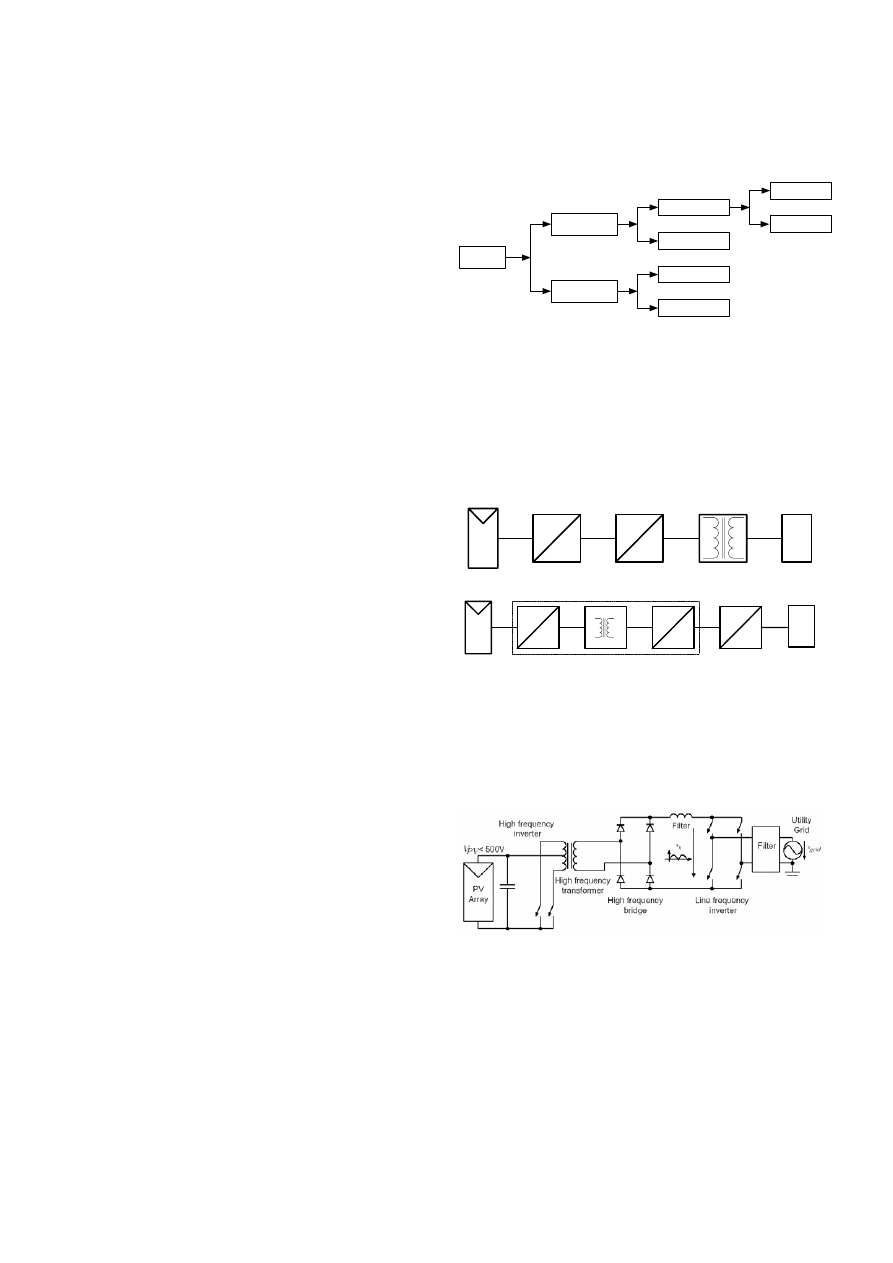
conditions. Also, the reliability of the plant may be limited
due to the dependence of power generation on a single
component: the failure of the central inverter results in that
the whole PV plant out of operation.

String inverter
Similar to the central inverter, the PV plant is divided into
several parallel strings. Each of the PV strings is assigned to
a designated inverter, the so-called "string inverter" (see Fig.
8c). String inverters have the capability of separate
Maximum Power Point (MPP) tracking of each PV string.
This increases the energy yield via the reduction of
mismatching and partial shading losses. These superior
technical characteristics lead increase the energy yield and
enhance the supply reliability. String inverters have evolved
as a standard in PV system technology for grid connected
PV plants.
An evolution of the string technology applicable for higher
power levels is the multi-string inverter [7]. It allows the
connection of several strings with separate MPP tracking
systems (via DC/DC converter) to a common DC/AC
inverter. Accordingly, a compact and cost-effective solution,
which combines the advantages of central and string
technologies, is achieved. This multi-string topology allows
the integration of PV strings of different technologies and of
various orientations (south, north, west and east). These
characteristics allow time-shifted solar power, which
optimizes the operation efficiencies of each string separately.
The application area of the multi-string inverter covers PV
plants of 3-10 kW.

Module integrated inverter
This system uses one inverter for each module (Fig. 8d).
This topology optimizes the adaptability of the inverter to
the PV characteristics, since each module has its own MPP
tracker. Although the module-integrated inverter optimizes
the energy yield, it has a lower efficiency than the string
inverter. Module integrated inverters are characterized by
more extended AC-side cabling, since each module of the
PV plant has to be connected to the available AC grid (e.g.
230 V/ 50 Hz). Also, the maintenance processes are quite
complicated, especially for facade-integrated PV systems.
This concept can be implemented for PV plants of about 50-
400 W peak.

PV inverter
The PV inverter technology has evolved quite a lot during
the last years towards maturity [42]. Still there are different
power configurations possible as shown in the Fig. 9.
The question of having a dc-dc converter or not is first of
all related to the PV string configuration. Having more
panels in series and lower grid voltage, like in US and Japan,
it is possible to avoid the boost function with a dc-dc
converter. Thus a single stage PV inverter can be used
leading to higher efficiency

.

The issue of isolation is mainly related to safety standards
and is for the moment only required in US. The drawback of
having so many panels in series is that MPPT is harder to
achieve especially during partial shading, as demonstrated in

[38]. In the following, the different PV inverter power
configurations are described in more details.

PV

Inverters

with DC-DC

converter

without DC-DC

converter

with isolation

without isolation

on the LF side

on the HF side

with isolation

without isolation

Fig. 9. Power configurations for PV inverters.

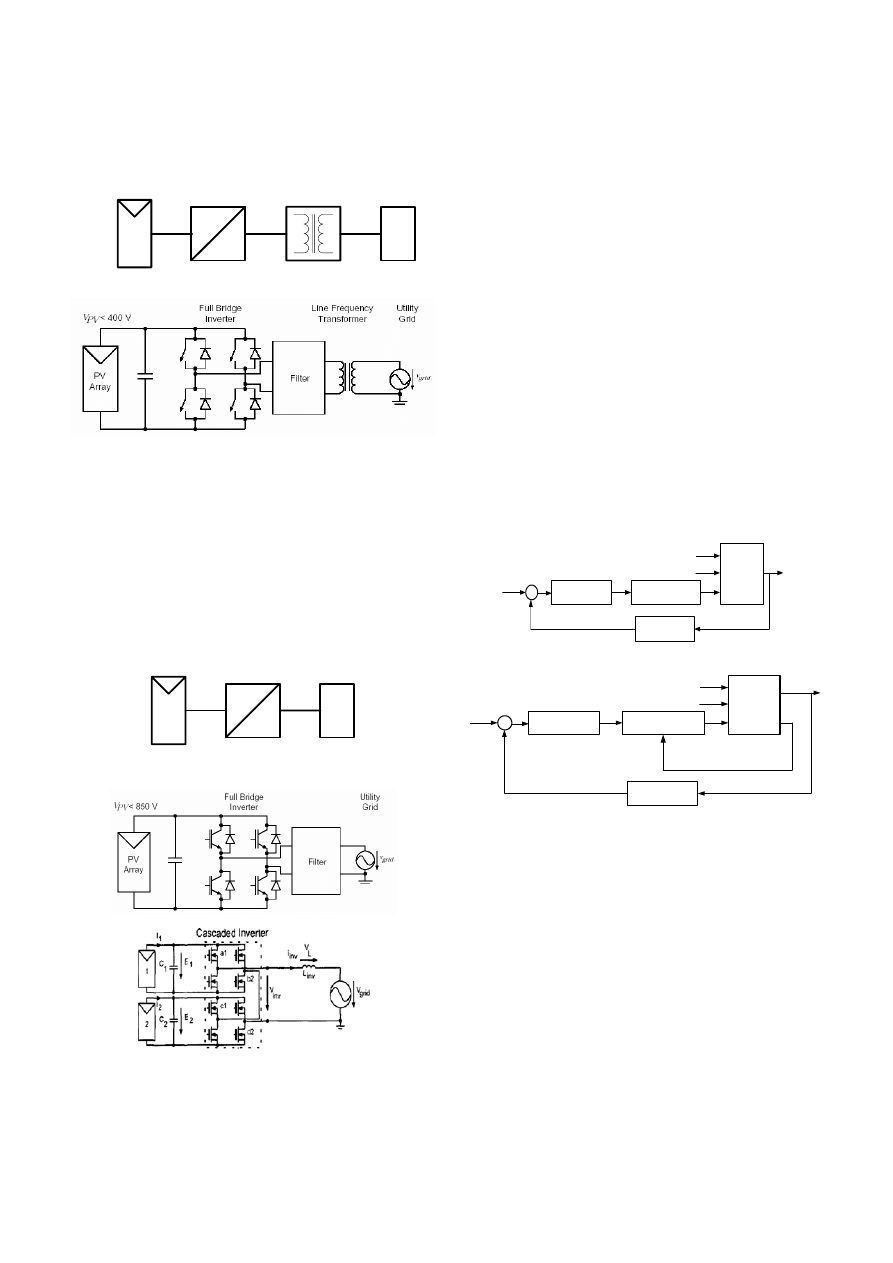
PV inverters with DC-DC converter and isolation
The isolation is typically acquired using a transformer that
can be placed on either the grid frequency side (LF) as
shown in Fig. 10a or on the high-frequency (HF) side in the
dc-dc converter as shown in Fig. 10b. The HF transformer
leads to more compact solutions but high care should be
taken in the transformer design in order to keep the losses
low.

DC

AC

Grid

PV

Array

DC

DC

(a)

DC

AC

Grid

PV

Array

DC

AC

AC

DC

(b)

Fig. 10. PV inverter system with DC-DC converter

and isolation transformer

a) on the Low Frequency (LF) side b) on the High Frequency (HF) side

In the Fig. 11 is presented a PV inverter with HF
transformer using an isolated push-pull boost converter [41]

Fig. 11. PV inverter with HF transformer in the dc-dc converter.

Also, the dc-ac inverter in this solution is a low cost
inverter switched at the line frequency. The new solutions
on the market are using PWM dc-ac inverters with IGBT’s
switched typically at 10-20 kHz leading to a better power
quality performance.
Other solutions for high frequency dc-dc converters with
isolations includes: full-bridge isolated converter, Single-
Inductor push-pull Converter (SIC) and Double-Inductor
Converter (DIC) as depicted in Fig. 12 [61].

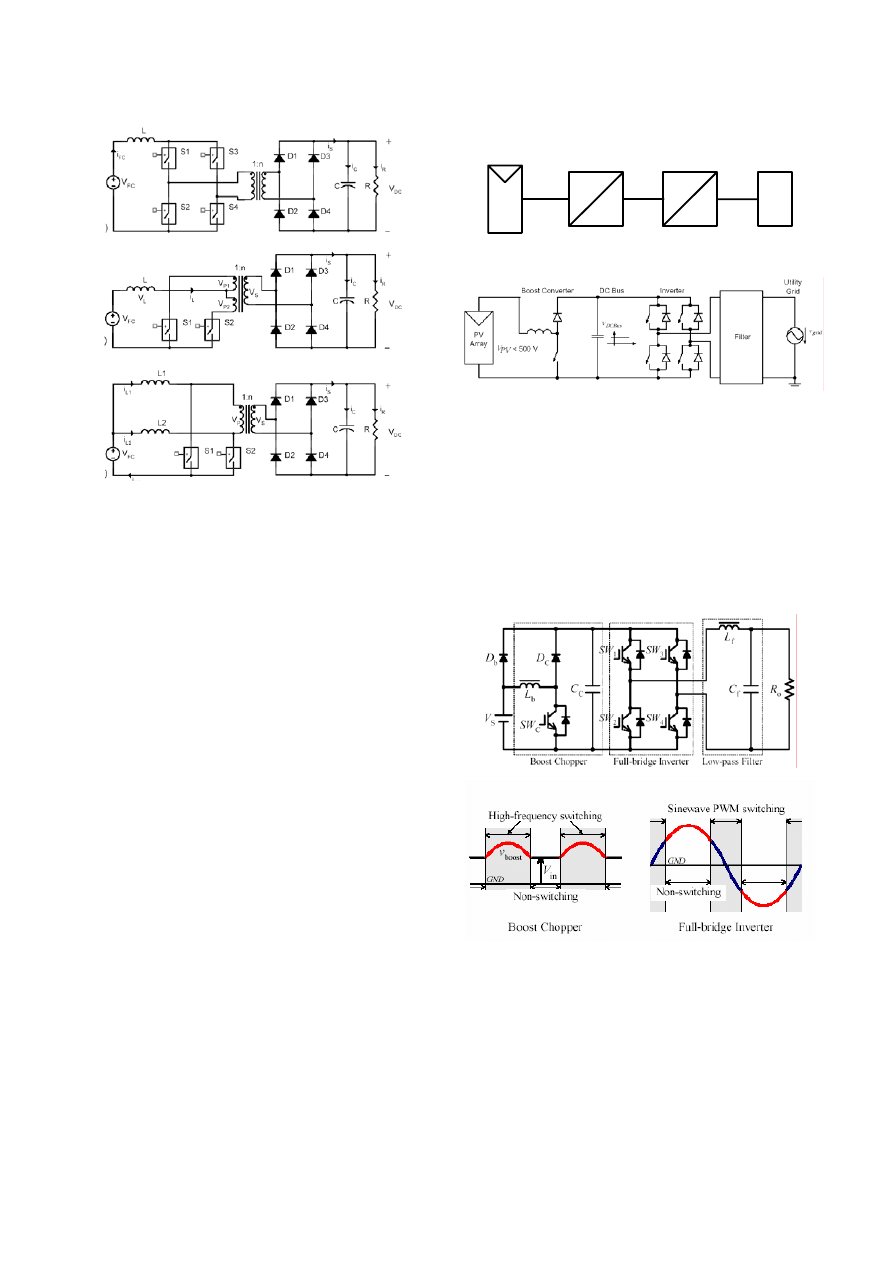
a)

b)

c)

Fig. 12. Dc-dc converter topologies with isolation. a) full-bridge; b) single-

inductor push-pull; c) double-inductor push-pull.

In order to keep the magnetic components compact high
switching frequencies in the range of 20 – 100 kHz are
typically employed. The full-bridge converter is usually
utilized at power levels above 750 W. The advantages of
this topology are: good transformer utilization – bipolar
magnetization of the core, good performance with current
programmed control – reduced DC magnetization of
transformer. The main disadvantages in comparison with
push-pull topology are the higher active part count and the
higher transformer ratio needed for boosting the dc voltage
to the grid level.
The single inductor push-pull converter can provide
boosting function on both the boosting inductor and
transformer, reducing the transformer ratio. Thus higher
efficiency can be achieved together with smoother input
current. On the negative side higher voltage blocking
switches are required and the transformer with tap point puts
some construction and reliability problems.
Those shortcomings can be alleviated using the double
inductor push-pull converter (DIC) where the boost inductor
has been split in two. Actually this topology is equivalent
with two interleaved boost converters leading to lower
ripple in the input current. The transformer construction is
more simple not requiring tap point. The single disadvantage
of this topology remains the need for an extra inductor.

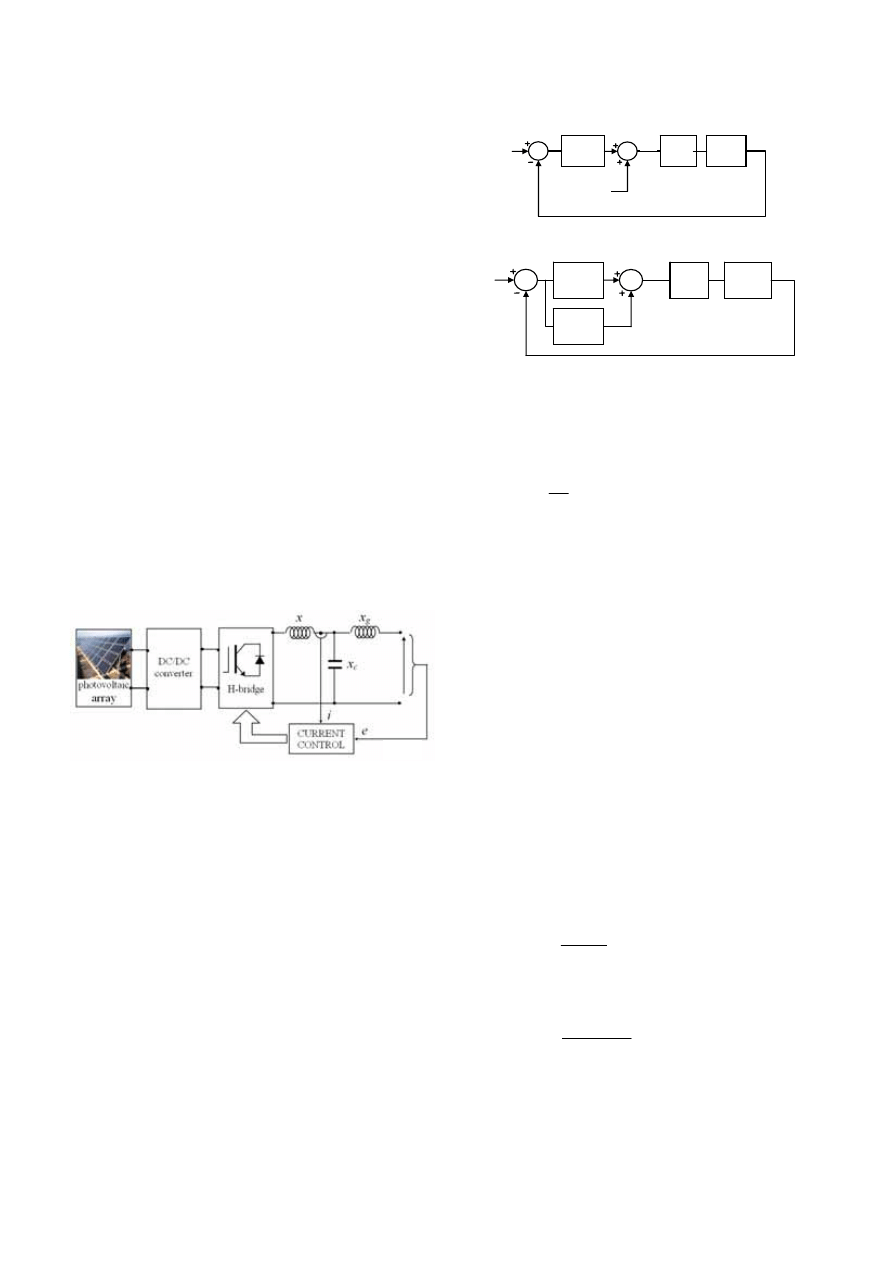
PV inverters with DC-DC converter without isolation
In some countries as the grid-isolation is not mandatory,
more simplified PV inverter design can be used, as shown in
Fig. 13.

DC

DC

DC

AC

Grid

PV

Array

(a)

(b)

Fig. 13. PV inverter system with DC-DC converter without isolation

transformer a) General diagram

b) Practical example with boost converter and full-bridge inverter [39]

In Fig. 13b a practical example [39] using a simple boost
converter is shown. Another novel transformerless topology
[39] featuring a high efficiency time-sharing dual mode
single-phase partially controlled sine-wave PWM inverter
composed of quasi time-sharing sine-wave boost chopper
with a new functional bypass diode D

b

in the boost chopper

side and complementary sine-wave PWM full-bridge
inverter (Fig. 14).

(a)

(b)

Fig. 14. Time-sharing dual-mode sinewave modulated

single-phase inverter with boost chopper [40]

a) Circuit system configuration. b) Operating principle.

PV inverters without DC-DC converter
The block diagram of this topology is shown in the Fig.
15a.

DC

AC

Grid

PV

Array

(a)

(b)

Fig. 15. PV inverter system without DC-DC converter

and with isolation transformer

a) general diagram b) practical example with full-bridge inverter and grid-

side transformer [39]

In Fig. 15b are presented two topologies of PV inverters
are presented where the line frequency transformer is used.
For higher power levels, self-commutated inverters using
thyristors are still being used on the market [39].

PV inverters without DC-DC converter and without
isolation
The block diagram of this topology is shown in Fig. 16a.

DC

AC

Grid

PV

Array

(a)

(b)

(c )

Fig. 16. Transformerless PV inverter system without DC-DC converter

a) general diagram b) typical example with full-bridge inverter [39]

c) multilevel [41]

In Fig. 16b, a typical transformerless topology is shown
using PWM IGBT inverters. This topology can be used
when a large number of PV panels are available connected
in series producing in excess of the grid voltage peak at all
times.
Another interesting PV inverter topology without boost
and isolation can be achieved using multilevel concept. Grid
connected photovoltaic systems with a five level cascaded
inverter is presented in Fig. 16c [41]. The redundant inverter
states of the five level cascaded inverter allow for a cyclic
switching scheme which minimizes the switching frequency,
equalizes stress evenly on all switches and minimizes the
voltage ripple on the DC capacitors.

IV.

C

ONTROL OF SINGLE

-

PHASE

PV-

INVERTERS

Control of DC-DC boost converter
In order to control the output dc-voltage to a desired value, a
control system is needed which can automatically can adjust
the duty cycle, regardless of the load current or input
changes. There are two types of control for the dc-dc
converters: the direct duty-cycle control and the current
control [62]. (See Fig. 17).

Compensator

Pulse-width

modulator

Converter

Sensor gain

v

ref

v

FC

(t)

i

load

(t)

d(t)

+

-

v

DC

(t)

Error

signal

Control

signal

Reference

input

(a)

Compensator

Comparator and

controller

Converter

Sensor gain

v

ref

v

FC

(t)

i

load

(t)

d(t)

+

-

v

DC

(t)

Error

signal

Control

signal

Reference

input

i

switch

(t)

i

switch

(t)

i

switch_ref

(t)

(b)

Fig. 17. Control strategies for switched dc-dc converters

a) direct duty-cycle control b) current control.

Duty-Cycle control
The output voltage is measured and then compared to the
reference. The error signal is used as input in the
compensator, which will calculate it from the duty-cycle
reference for the pulse-width modulator.

Current Control
The converter output is controlled by the choice of the
transistor peak current. The control signal is a current and a
simple control network switches on and off the transistor
such its peak current follows the control input. The current
control, in the case of an isolated boost push-pull converter
has some advantages against the duty-cycle control like
simpler dynamics (removes one pole from the control-to
output transfer function). Also as it uses a current sensor it

can provide a better protection of the switch by limiting the
current to acceptable levels.
Another issue is the transformer saturation. In the
transformer a dc bias current generated by small voltage
imbalances can be induced due to the small differences in
boost inductors and/or switches. The dc current bias will
increase or decrease the transistor currents. The current
control will alter the duty cycles in the switch in a way that
these imbalances tend to disappear and the transformer volt-
second balance to be maintained. Finally, the current
control is better suited to modularity where current sharing
needs to be solved when running in parallel.
Among the drawbacks of the current control it can be
mentioned that it requires an extra current sensor and it has a
susceptibility to noise and thus light filtering of feedback
signals is required.

Control of DC-AC grid converter
For the grid-connected PV inverters in the range of 1-5
kW, the most common control structure for the dc-ac grid
converter is using a current-controlled H-bridge PWM
inverter having a low-pass output filter. Typically L filters
are used but the new trend is to use LCL filters that have a
higher order filter (3

rd

) which leads to more compact design.

The drawback is that due to its own resonance frequency it
can produce stability problems and special control design is
required [43]. A typical dc-ac grid converter with LCL filter
is depicted in Fig. 18.

u

g

Fig.18. The H-bridge PV coverter connected to the grid

through an LCL filter

The harmonics level in the grid current is still a
controversial issue for PV inverters. The IEEE 929 standard
from year 2000 allows a limit of 5% for the current Total
Harmonic Distortion (THD) factor with individual limits of
4% for each odd harmonic from 3rd to 9th and 2% for 11th
to 15th while a recent draft of European IEC61727 suggests
something similar. These levels are far more stringent than
other domestic appliances such as IEC61000-3-2 as PV
systems are viewed as generation sources and so they are
subject to higher standards than load systems.

Classical PI control with grid voltage feed-forward (U

g

)

[11] as depicted in Fig. 19a is commonly used for current-
controlled PV inverters, but this solution exhibits two well
known drawbacks: inability of the PI controller to track a
sinusoidal reference without steady-state error and poor
disturbance rejection capability. This is due to the poor
performance of the integral action.

i

i

*

i

i

G

PI

(s)

G

d

(s)

G

f

(s)

i

i

u

i

*

u

g

(a)

i

i

*

i

i

G

c

(s)

G

h

(s)

G

d

(s)

G

f

(s)

i

i

u

i

*

(b)

Fig. 19. The current loop of PV inverter.

a) with PI controller; b) with P+Resonant (PR) controller

The PI current controller G

PI

(s) is defined as:

( )

I

PI

P

K

G s

K

s

=

+

(1)

In order to get a good dynamic response, a grid voltage
feed-forward is used, as depicted in Fig. 19a. This leads in
turn to stability problems related to the delay introduced in
the system by the voltage feedback filter.
In order to alleviate these problems, a second order
generalized integrator (GI) as reported in [63] can be used.
The GI is a double integrator that achieves an infinite gain at
a certain frequency, also called resonance frequency, and
almost no gain exists outside this frequency. Thus, it can be
used as a notch filter in order to compensate the harmonics
in a very selective way. This technique has been primarily
used in three-phase active filter applications as reported in
[63] and also in [64] where closed-loop harmonic control is
introduced. Another approach reported in [65] where a new
type of stationary-frame regulators called P+Resonant (PR)
is introduced and applied to three-phase PWM inverter
control. In this approach the PI dc-compensator is
transformed into an equivalent ac-compensator, so that it has
the same frequency response characteristics in the
bandwidth of concern. The current loop of the PV inverter
with PR controller is depicted in Fig. 19b.
The P+Resonant (PR) current controller G

c

(s) is defined as

[43], [63]:

2

2

( )

c

P

I

o

s

G s

K

K

s

ω

=

+

+

(2)

The harmonic compensator (HC) G

h

(s) as defined in [43]:

(

)

2

2

3,5,7

( )

h

Ih

h

o

s

G s

K

s

h

ω

=

=

+

∑

(3)

is designed to compensate the selected harmonics 3

rd

, 5

th

and

7

th

as they are the most prominent harmonics in the current

spectrum. A processing delay typical equal to T

s

for the

PWM inverters [62] is introduced in

. The filter

transfer function G

f

(s) is expressed in (4) [59].

( )

d

G s

(

)

(

)

2

2

2

2

( )

1

( )

( )

LC

i

f

i

i

res

s

z

i s

G s

u s

L s s

ω

+

=

=

+

(4)

where

and

1

2

LC

g

f

z

L C

−

⎡

⎤

= ⎣

⎦

(

)

2

2

i

g

LC

res

i

L

L

z

L

ω

+

⋅

=

The current error - disturbance ratio rejection capability at
null reference is defined as:

(

)

*

0

( )

( )

( )

1

( )

( )

( )

( )

i

f

g

c

c

d

i

G s

s

u s

G s

G s

G s G s

ε

=

=

+

+

⋅

⋅

f

(5)

where:

ε is current error and the grid voltage u

g

is

considered as the disturbance for the system.
The Bode plots of disturbance rejection for the PI and PR
controllers are shown in Fig 20. As it can be observed, The
PR provides much higher attenuation for both fundamental
and lower harmonics then PI. The PI rejection capability at
5

th

and 7

th

harmonic is comparable with that one of a simple

proportional (P) controller, the integral action being
irrelevant.

-150

-100

-50

0

10

1

10

2

10

3

-540

-450

-360

-270

PR+HC
PI
P

Magnitude [dB]

Phase angle (degrees)

Frequency [Hz]

Fig. 20. Bode plot of disturbance rejection (current error ratio disturbance)

of the PR+HC, P and PR current controllers.

Thus it is demonstrated the superiority of the PR controller
in respect to the PI controller in terms of harmonic current
rejection. In [43] the discrete implementation into a low-cost
fixed-point DSP is demonstrated. In Fig. 21 some
experimental results with a 3 kW PV inverter are shown
demonstrating the harmonic compensation using more
advanced controllers.

0

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.0

-25

-20

-15

-10

-5

0

5

10

15

20

25

tim e[sec]

Ig (exp) [5A/div]
Ug (exp) [100/div]

(a)

0

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.0

-25

-20

-15

-10

-5

0

5

10

15

20

25

time[sec]

Ig (exp) [5A/div]
Ug (exp) [100/div]

(b)

0

0 . 0 0 5

0 . 0 1

0 . 0 1 5

0 . 0 2

0 . 0 2 5

0 . 0 3

0 . 0 3 5

0 . 0 4

-2 5

-2 0

-1 5

-1 0

-5

0

5

1 0

1 5

2 0

2 5

t im e [ s e c ]

Ig (e x p ) [ 5 A / d iv]
U g (e x p ) [ 1 0 0 / d iv]

(c)

Fig. 21. Experimental results at 3kW. Grid voltage and current. a) with PI

controller. b) with PR; c) with PR+HC.

The issue of stability when several PV inverters are
running in parallel on the same grid is becoming more and
more important especially when LCL filters are used. In
[44] it is shown that in the case of a concentration of several
hundreds of solar roofs in Holland, resonance frequencies in
the range of 1-2 kHz are occurring as a result of the grid
interaction with the PV inverter. Thus, special attention is
required when designing the current control.

MPPT

In order to capture the maximum power, a maximum
power point tracker (MPPT) is required. The maximum
power point of PV panels is a function of solar irradiance
and temperature as depicted in Fig. 6. This function can be
implemented either in the dc-dc converter or in the dc-ac

converter. Several algorithms can be used in order to
implement the MPPT as followings [44].

Perturb and Observe
The most commonly used MPPT algorithm is Perturb and
Observe (P&O), due to its ease of implementation in its
basic form [45]. Fig. 6 shows the characterstic of a PV array,
which has a global maximum at the MPP. Thus, if the
operating voltage of the PV array is perturbed in a given
direction and dP/dV > 0, it is known that the perturbation
moved the operating point toward the MPP. The P&O
algorithm would then continue to perturb the PV array
voltage in the same direction. If dP/dV < 0, then the change
in operating point moved the PV array away from the MPP,
and the P&O algorithm reverses the direction of the
perturbation. A problem with P&O is that it oscillates
around the MPP in steady state operation. It also can track in
the wrong direction, away from the MPP, under rapidly
increasing or decreasing irradiance levels. There are several
variations of the basic P&O that have been designed to
minimize these drawbacks. These include using an average
of several samples of the array power and dynamically
adjusting the magnitude of the perturbation of the PV
operating point.

Incremental Conductance
The incremental conductance algorithm seeks to overcome
the limitations of the P&O algorithm by using the PV array's
incremental conductance to compute the sign of dP/dV
without a perturbation [45]. It does this using an expression
derived from the condition that, at the MPP, dP/dV = 0.
Beginning with this condition, it is possible to show that, at
the MPP dI/dV = -I/V. Thus, incremental conductance can
determine that the MPPT has reached the MPP and stop
perturbing the operating point. If this condition is not met,
the direction in which the MPPT operating point must be
perturbed can be calculated using the relationship between
dI/dV and -I/V. This relationship is derived from the fact
that dP/dV is negative when the MPPT is to the right of the
MPP and positive when it is to the left of the MPP. This
algorithm has advantages over perturb and observe in that it
can determine when the MPPT has reached the MPP, where
perturb and observe oscillates around the MPP. Also,
incremental conductance can track rapidly increasing and
decreasing irradiance conditions with higher accuracy than
perturb and observe. One disadvantage of this algorithm is
the increased complexity when compared to perturb and
observe. This increases computational time, and slows down
the sampling frequency of the array voltage and current.

Parasitic Capacitance
The parasitic capacitance method is a refinement of the
incremental conductance method that takes into account the
parasitic capacitances of the solar cells in the PV array [45].
Parasitic capacitance uses the switching ripple of the MPPT
to perturb the array. To account for the parasitic capacitance,
the average ripple in the array power and voltage, generated
by the switching frequency, are measured using a series of
filters and multipliers and then used to calculate the array

conductance. The incremental conductance algorithm is then
used to determine the direction to move the operating point
of the MPPT. One disadvantage of this algorithm is that the
parasitic capacitance in each module is very small, and will
only come into play in large PV arrays where several
module strings are connected in parallel. Also, the DC-DC
converter has a sizable input capacitor used the filter out
small ripple in the array power. This capacitor may mask the
overall effects of the parasitic capacitance of the PV array.

Constant Voltage
This algorithm makes use of the fact that the MPP voltage
changes only slightly with varying irradiances, as depicted
in Fig. 6. The ratio of VMP/VOC depends on the solar cell
parameters, but a commonly used value is 76% [45]. In this
algorithm, the MPPT momentarily sets the PV array current
to zero to allow a measurement of the array's open circuit
voltage. The array's operating voltage is then set to 76% of
this measured value. This operating point is maintained for a
set amount of time, and then the cycle is repeated. A
problem with this algorithm is available energy is wasted
when the load is disconnected from the PV array, also the
MPP is not always located at 76% of the array’s open circuit
voltage.

Anti-islanding
In addition to the typical power quality regulations
concerning the harmonic distortion and EMI limits, the grid-
connected PV inverters must also meet specific power
generation requirements like the islanding detection, or even
certain country-specific technical recommendations for
instance the grid impedance change detection (in Germany).
Such extra-requirements contribute to a safer grid-operation
especially when the equipment is connected in dispersed
power generating networks but impose additional effort to
readapt the existing equipments.
The European standard EN50330-1 (draft) [46] describes
the ENS (the German abbreviation of Mains monitoring
units with allocated Switching Devices) requirement, setting
the utility fail-safe protective interface for the PV converters.
The goal is to isolate the supply within 5 seconds after an
impedance change of Z = 0.5

Ω, which is associated with a

grid failure. The main impedance is typically detected by
means of tracking and step change evaluation at the
fundamental frequency. Therefore, a method of measuring
the grid impedance value and its changes should be
implemented into existing PV-inverters.
One solution is to attach a separate device developed only
for the measuring purpose as depicted in Fig. 22a.

(a)

(b)

Fig. 22. Grid-impedance measurement for PV inverters. a) using external

device; b) embedded on the inverter control using harmonic injection.

This add-on option is being commonly used in the
commercial PV inverters, but the new trend is to implement
this function embedded into the inverter control without
extra hardware. Numerous publications exist in this field,
which offer measuring solutions for the grid impedance for a
wide frequency range from dc up to typically 1 kHz [47].
Unfortunately, not always can these methods easily be
embedded into a non-dedicated platform, i.e. PV-inverters
featuring typically a low-cost DSP. Specific limitations like
real-time computation, A/D conversion accuracy and fixed-
point numerical limitation, are typically occurring.
A novel approach presented in [48], [49] estimates the grid
impedance on-line with the purpose of detection the step
change of 0.5

Ω as required in [46] as shown in Fig. 22b.

The solution is found by injecting a test signal through the
inverter modulation process. This signal, an interharmonic
current with a frequency close to the fundamental,
determines a voltage drop due to the grid impedance, which
is measured by the existing PV-inverter sensors. Then, the
same CPU unit that makes the control algorithm carries out
the calculations and gives the grid impedance value [48].

This approach provides a fast and low cost solution to meet

the required standards and was succesfully implemented on
a TMS320F24x 16-bit fixed point DSP platform as an add-
on to the existing control.

V.

C

ONTROL OF THREE

-

PHASE INVERTERS

The control of a three-phase inverter connected to the grid

has more in common with the control of an active
rectifier/filter rather than with the control of an adjustable
speed drive. In fact with the first the distributed inverter
shares the characteristic to be connected to the grid on the ac
side, while with second it shares the common characteristic
to have less responsibilities in the management of the dc-
link voltage that is usually controlled by another converter
stage. Hence from the control perspective the three-phase
distributed inverter has an advantage over the rectifier and a
disadvantage over the inverter for the motor.

Its control issues will be discussed starting from its

mathematical model both with L-filter and LCL-filter on the
grid side. Then simple controls as well as a few advanced
methods will be introduced and briefly discussed. Finally
some advanced topics and experimental results are shown.

Mathematical Model of the L-filter inverter
The state of the three-phase inverter is modelled by means
of a switching space-vector defined with the switching

functions

(j = a, b, c)

)

(t

p

j

(

)

2

a

b

c

2

p(t)

p (t)

p (t)

p (t)

3

=

+ α⋅

+ α ⋅

(6)

then if the inverter is connected to the grid through an L-
filter (Fig. 23).

d ( )

( )

( )

( )

d

i t

v t

e t

Ri t

L

t

=

+

+

(7)

o

1

v(t)

p(t)v (t)

2

=

(8)

Fig. 23. L-filter inverter connected to the grid.

assuming to neglect the dc voltage dynamics as the dc
voltage v

o

(t) is an input to the system. Moreover

)

(t

v

is the

space-vector of the inverter input voltages;

)

(t

i

is the

space-vector of the inverter input curre

nts;

)

(t

e

is the

space-vector of the input line voltages.

The mathematical model written in the state space form is

d ( )

1

1

( )

( )

( ) ( )

d

2

o

i t

Ri t

e t

p t v t

t

L

⎡

⎤

=

−

−

+

⎢

⎥

⎣

⎦

(9)

A commonly used approach in analysing three-phase

systems is to adopt a dq-frame that rotates at the angular
speed

ω (where ω = 2πf and f is the fundamental frequency

of the power grid’s voltage waveform). The space-vectors
which express the inverter electrical quantities are projected
on the d-axis and q-axis. As a consequence if a space-vector
with constant magnitude rotates at the same speed of the
frame, it has constant d- and q- components while if it
rotates at a different speed or it has a time-variable
magnitude it has pulsating components. Thus in a dq-frame
rotating at the angular speed

ω (7) becomes

( )

( )

( )

( )

( ) ( )

( )

( )

( )

( )

( ) ( )

1

1

2

1

1

2

d

q

d

d

d

q

d

q

q

q

di t

i t

Ri t

e t

p t v t

dt

L

di t

i t

Ri t

e t

p t v t

dt

L

ω

ω

⎧

o

o

⎡

⎤

−

=

−

−

+

⎪

⎢

⎥

⎣

⎦

⎪

⎨

⎡

⎤

⎪

+

=

−

−

+

⎢

⎥

⎪

⎣

⎦

⎩

(10)

(10) shows how in the dq-frame the d- and q- differential

Mathematical Model of the LCL-filter inverter

s reported in

o

Fig. 24. LCL-filter inverter connected to the grid.

C Current control

trol (CC) is usually adopted because the

cu

ntages. The

fe

he current control is the most inner loop of a

ca

equations for the current are dependent due to the cross-
coupling terms

ωi

q

(t) and

ωi

d

(t).

In (11) the LCL-filter based inverter model i

rder to highlight the increased complexity of the system.

The system is shown in Fig. 24.

A

The ac current con

rrent controlled converter exhibits, in general, better

safety, better stability and faster response [11].

This solution ensures several additional adva

edback loop also results in some limitations, such as that

fast-response voltage modulation techniques must be
employed, like PWM. Optimal techniques, which use
precalculated switching patterns within the ac period, cannot
be used, as they are not oriented to ensure current waveform
control [11].

Generally t

scade control that employ a dc-link voltage level

management system and active and reactive power
controller as shown in Fig. 25.

1

1

1

1

1

1

1

1

1

1

2

2

2

2

2

2

2

2

2

2

0

0

0

1

0

0

0

1

1

0

0

0

1

1

0

0

0

1

0

0

0

1

0

0

0

−

−

⎢

⎥

⎢

⎥

⎢

⎥

−

−

−

−

⎢

⎥

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

=

+

⎢

⎥

⎢

⎥

⎢

⎥

−

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎣

⎦

−

−

⎢

⎥

⎢

⎥

⎢

⎥

−

−

⎢

⎥

⎣

⎦

f

f

f

f

d

d

q

q

C d

C d

f

f

C q

C q

f

f

d

d

q

q

L

L

R

i

i

L

L

i

i

v

v

C

C

d

v

v

dt

C

C

i

i

R

i

i

L

L

R

L

L

ω

ω

ω

ω

ω

ω

1

1

2

2

1

0

0

0

0

0

1

0

0

0

0

0

0

0

1

0

0

0

0

0

1

0

0

0

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

⎢

⎥

⎡ ⎤

⎡

⎢

⎥

⎢

⎥

+

⎢ ⎥

⎢

⎢

⎥

⎢

⎥

⎣ ⎦

⎣

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎣

⎦

d

d

q

q

L

e

v

L

e

v

L

L

1

⎡

⎤

R

The use of an LCL-filter claims for a deep dynamic and

stability analysis of the current control loop [50]. In order to
highlight the stability problems that arise from the use of an
LCL-filter it is sufficient to show the d- or q-system plant in
Laplace domain. If the converter side current is sensed, the
system plant is

(

)

(

)

2

2

2

2

2

( )

1

( )

( )

LC

res

s

z

i s

G s

v s

L s s

ω

+

=

=

+

(12)

If the grid side current is sensed, the plant for control is

(

)

2

2

2

2

( )

1

( )

( )

LC

res

z

i s

G s

v s

L s s

ω

=

=

+

(13)

where

1

2

1

LC

f

z

L C

−

⎡

⎤

= ⎣

⎦

and

(

)

2

2

1

2

2

res

LC

L

L z

L

ω

=

+

.

In both cases the two poles related to the resonance of the
LCL-filter challenges the current control instability,
particularly the second one (sensing of the grid current)
generally leads to a more stable behavior [50].

Two axis-based current control

The most used control technique is the two axis-based

method [11]. Then if the two-axis system is a stationary

αβ-

frame, the proportional plus resonant controller can be
adopted [43] and it is

2

2

0

2

2

0

0

( )

0

i

p

PR

i

p

K s

K

s

D

s

K s

K

s

αβ

ω

ω

⎡

⎤

+

⎢

⎥

+

⎢

⎥

= ⎢

⎥

+

⎢

⎥

+

⎢

⎥

⎣

⎦

(14)

If the frame is a rotating dq-frame, classical PI controllers
can be used

0

( )

0

i

p

PI

dq

i

p

K

K

s

D

s

K

K

s

⎡

⎤

+

⎢

⎥

= ⎢

⎥

⎢

⎥

+

⎢

⎥

⎣

⎦

(15)

If this controller is transformed into an

αβ-frame then

⎤

⎥

⎦

(11)

Fig. 25. Block diagram of a typical three-phase distributed inverter.

0

2

2

2

2

0

0

0

2

2

2

2

0

0

( )

i

i

p

PI

i

i

p

K s

K

K

s

s

D

s

K

K

K

s

s

αβ

ω

ω

ω

ω

ω

ω

⎡

⎤

+

⎢

⎥

+

+

⎢

⎥

= ⎢

⎥

−

+

⎢

⎥

+

+

⎢

⎥

⎣

⎦

s

(16)

In Eq. (16) it is equal to (14) except for non-diagonal terms.
Hence the PI controller in the dq-frame and PR controller in
the

αβ-frame can achieve similar performances.

In the case of a dq-frame, if it is oriented such as the d-
axis is aligned on the grid voltage vector the control is called
Voltage Oriented Control (VOC) (Fig. 26). The reference
current d-component i

*

d

is controlled to manage the active

power flow while the reference current q-component i

*

q

is

controlled to manage the reactive power flow. To have

the

grid current vector in phase with the grid voltage vector, i

*

q

should be zero.

Grid voltage harmonic compensators

The grid voltage is usually affected by a background

distortion that can result in a high harmonic distortion of the
grid current. This problem can be solved both in a stationary

αβ-frame and in a rotating dq-frame. In the first case it is
sufficient to plug in other resonant controller also called
harmonic compensators

(

)

2

2

3,5,7

0

( )

R

ih

h

s

G s

k

s

h

αβ

ω

=

=

+

⋅

∑

(17)

where h is the order of the harmonic to be compensated.

If the controller adopts a rotating dq-frame approach it is

possible to introduce other dq-frame rotating at multiple
speed in respect to the fundamental one and adopting
standard PI-controllers in each of them. In both the cases it
is necessary that the harmonics to be compensated stay
within the bandwidth of the current controller otherwise
stability problems may arise [37].

Fig. 26. Voltage Oriented Control based on the use of a rotating

dq

-frame.

Current control active damping
This solution seems very attractive especially in
applications above several kW, where the use of a damping
resistor increases the encumbrances, the losses could claim
for forced cooling and the efficiency decrement becomes a
key point. In [51] a lead-lag network has been used on the
filter capacitor voltage and it is possible to avoid the use of

new sensors because this voltage is near to the grid, which is
normally sensed. Moreover, in [52] an interesting approach
to perform active damping has been proposed: a virtual
resistor is added. The virtual resistor is an additional control
algorithm that makes the LCL-filter behaving as if there was
a real resistor connected to it. However, an additional
current sensor is needed if the virtual resistor is connected in
series to the filter inductor or capacitor. Further an
additional voltage sensor is needed, if it is connected in
parallel. Basically all these approaches are multiloop-based
[53] while an alternative solution consists of adopting a
more complex controller acting as a digital filter around the
resonance frequency of the LCL-filter [50].

Direct power control
In the last years the most interesting emerging technique has
been the direct power control developed in analogy to the
well known direct torque control used for drives. In DPC
there are no internal current loops and no PWM modulator
block because the converter switching states are
appropriately selected by a switching table based on the
instantaneous errors between the commanded and estimated
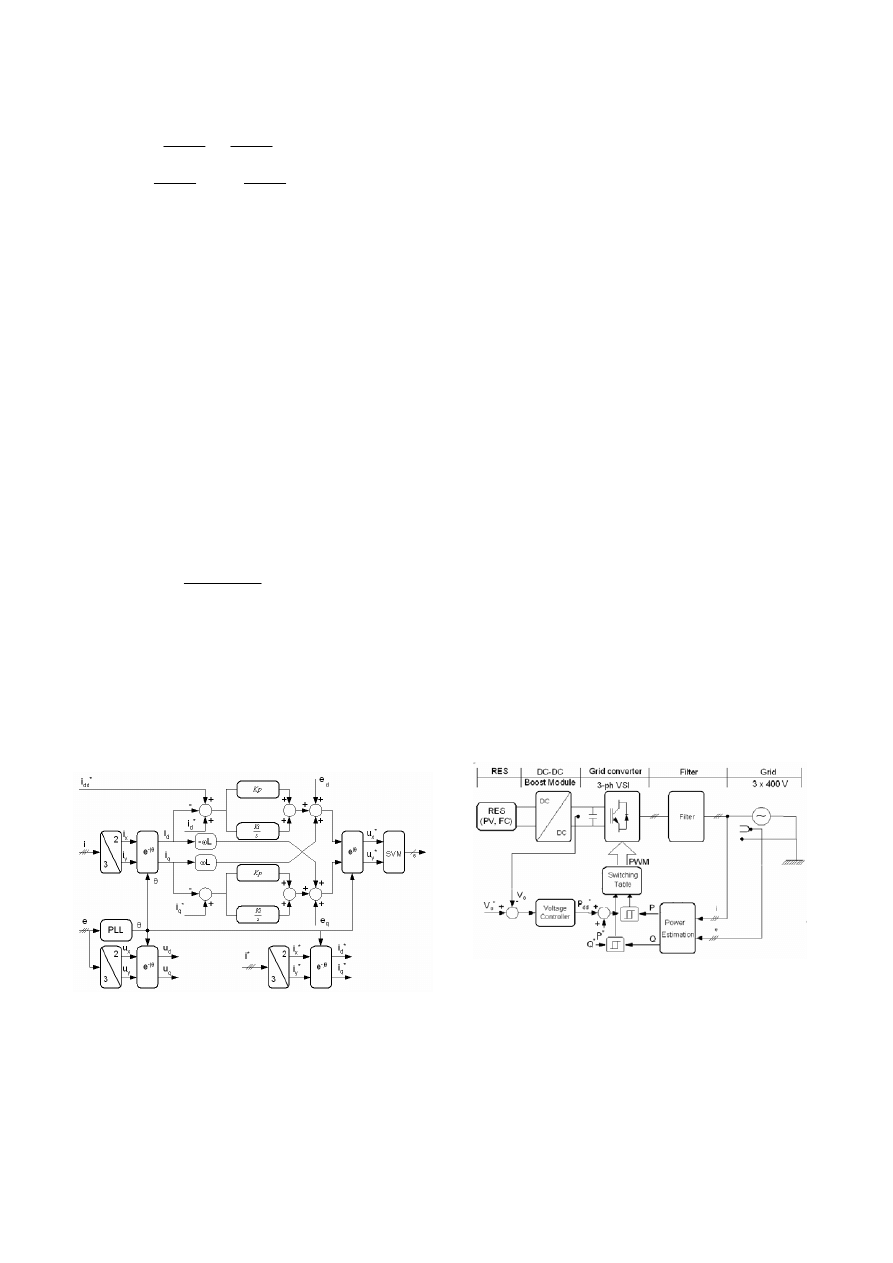
values of active and reactive power [11], [54], [55] see Fig.
27. The main advantage of the DPC is in its simple
algorithm while the main disadvantage is the need for a high
sampling frequency to obtain satisfactory performance.

Reduction of the number of sensors
The basic number of needed sensors is 4 (two ac currents
and two ac voltages). However this number can be reduced
avoiding the use of grid voltage vector with implementing a
virtual sensor or using a zero crossing detector in order to
have the phase reference for the current. Moreover if a
feedforward current control technique is adopted the grid
current sensors can be avoided but it is essential to provide a
method for overcurrent protection in industrial applications.

Fig. 27. Direct Power Control based on the active and reactive power

calculation.

In [56] an algorithm to estimate the position of line
voltage is presented. The proportional-plus-integral current
regulator is modified to obtain the angle error signal driving
an observer, similar in structure to a phase-locked loop,
which provides the angle of line voltages.

Non-ideal conditions
The non-ideal conditions are many and they can affect
very much the overall system performance such as too long

computation time, presence of acquisition filters, ac phase
unbalance, location of the grid voltage sensors after a
dominant reactance and passive damping if an LCL-filter is
used. A proper design to take them into consideration them
should be provided [57].
It is well known that the grid unbalance causes even
harmonics at the dc output and odd harmonics in the input
current [58]. Some solutions have been studied such as the
use of negative sequence in the reference current that
unfortunately leads to uncontrollability of the power factor
or the use of two current controllers for positive and
negative sequences, which also can create stability problems.

EMC-issues
The main EMC-issues are related to the low frequency
range and thus to the correct control of the current. Thus the
use of a LCL-filter on the ac side is an interesting solution:
the reduced values of the inductance can be achieved and
the grid current is almost ripple free. The design of the LCL-
filter has been investigated [59].

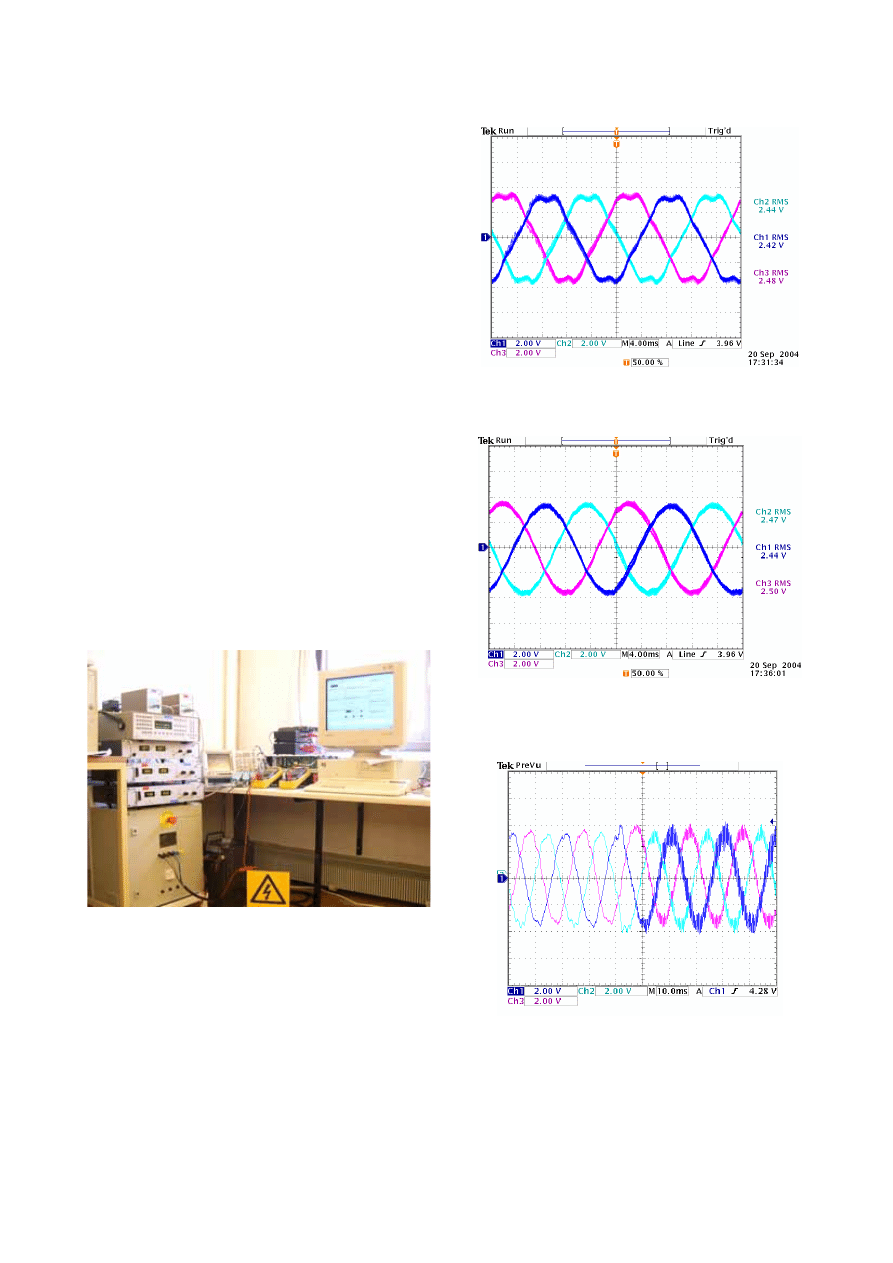
Some tests results, obtained on the set-up shown in Fig.

28, are reported in order to evaluate the impact of the non-
ideal conditions on the behaviour of a PR-based controller in

αβ-frame (Fig. 29), the use of harmonic compensator in a
stationary

αβ-frame to mitigate these effects (Fig. 30) and

finally the effect of active damping (Fig. 31).

Results

Fig. 28. Laboratory set-up to test three-phase power converter control.

Fig. 29. Compensation of grid background distortion: grid currents [2

A/div] and grid voltage [100 V/div] (sampling/switching 10 kHz, active

power 2 kW, PR-controllers in a

αβ-frame).

Fig. 30. Compensation of grid background distortion: grid currents [2

A/div] and grid voltage [100 V/div] (sampling/switching 10 kHz, active

power 2 kW, PR-controllers in a

αβ-frame with 5

th

and 7

th

harmonic

compensators).

Fig. 31. Control change from active damping to no damping (t=40 ms): grid

currents [2 A/div] (sampling/switching 10 kHz, active power 2 kW, PR-

controllers in a

αβ-frame).

VI.

C

ONVERTER

T

OPOLOGIES FOR

W

IND

T

URBINES

In a fixed speed wind power conversion system, the

power may be limited aerodynamically either by stall, active

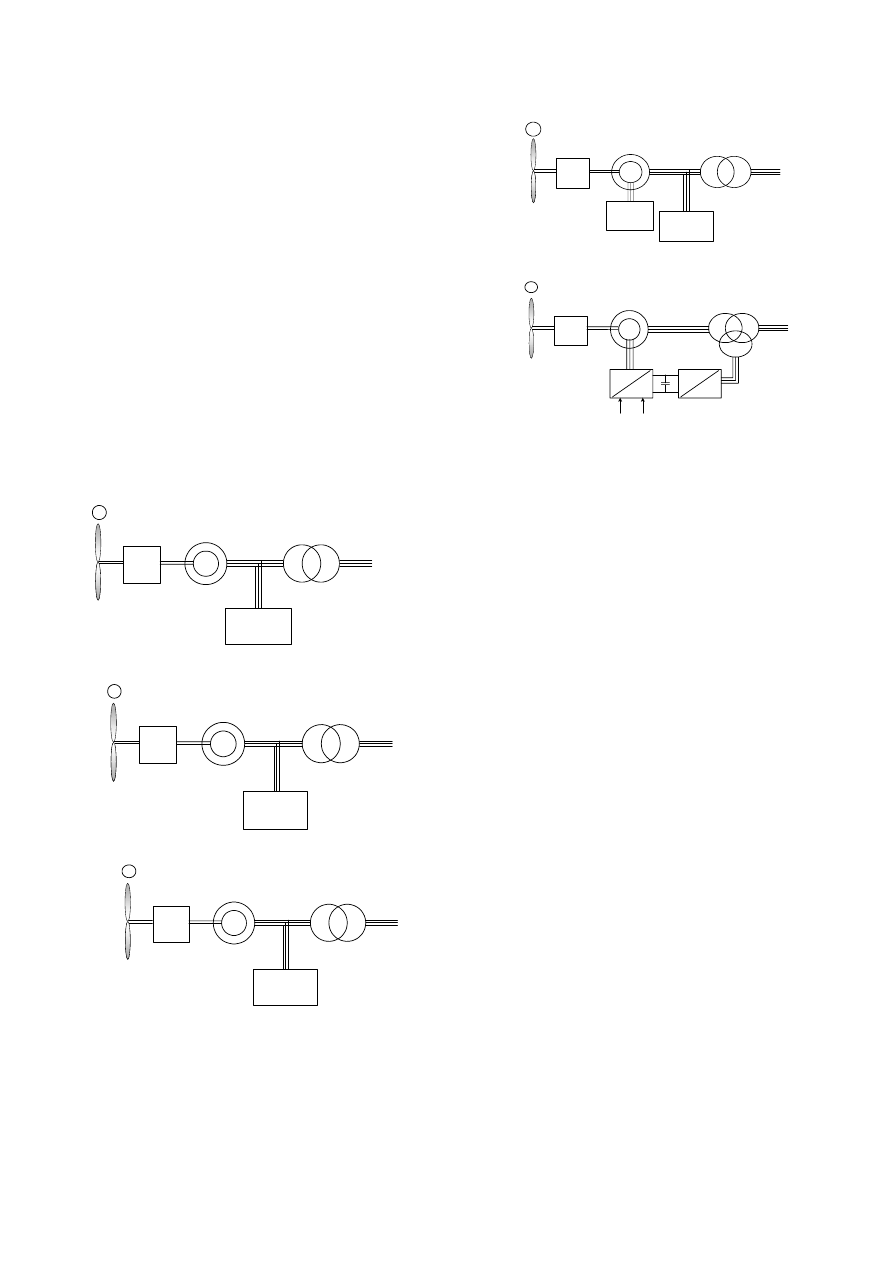
stall or by pitch control [6], [7]. Normally induction
generators are used in fixed speed systems, which are almost
independent of torque variation and operate at a fixed speed
(slip variation of 1-2%). Fig. 32 shows different topologies
for the first category of wind turbines.

All three systems are using a soft-starter (not shown in

Fig. 32) in order to reduce the inrush current and thereby
limit flicker problems on the grid. They also need a reactive
power compensator to reduce (almost eliminate) the reactive
power demand from the turbine generators to the grid.

It is usually done by continuously switching capacitor

banks following the production variation (5-25 steps). Those
solutions are attractive due to cost and reliability but they
are not able (within a few ms) to control the active power
very fast. The generators have typically a pole-shift
possibility in order to maximize the energy capture.
The next category is variable speed systems [6]-[36] where
pitch control is typically used. Variable speed wind turbines
may be further divided into two parts, one with partially
rated power electronic converters and one with fully rated
power electronic converters.

Gear

Induction

generator

Pitch

Grid

Reactive

compensator

I

(a)

Gear

Induction

generator

Stall

Grid

Reactive

compensator

II

(b)

r

com

(c)

Fig. 32. Wind turbine systems without power converter but with

aerodynamic power control.

Pitch controlled (System I) b) Stall controlled (System II) c) Active stall

controlled (System III).

Gear

W ounded Rotor

Induction

generator

Pitch

Grid

Reactive

com pensator

IV

Resistance

control

with PE

(a)

Gear

Doubly-fed

induction generator

Pitch

Grid

V

DC

AC

AC

DC

P

ref

Q

ref

(b)

Fig. 33. Wind turbine topologies with partially rated power electronics and

limited speed range, (a) Rotor-resistance converter (System IV) (b) Doubly-

fed induction generator (System V).

Fig. 33 shows wind turbines with partially rated power

electronic converters that are used to obtain an improved
control performance. Fig. 33a shows a wind turbine system
where the generator is an induction generator with a
wounded rotor. An extra resistance is added in the rotor,
which can be controlled by power electronics. This is a
dynamic slip controller and it gives typically a speed range
of 2-10 %. The power converter for the rotor resistance
control is for low voltage but high currents. At the same
time an extra control freedom is obtained at higher wind
speeds in order to keep the output power fixed. This solution
still needs a soft-starter and a reactive power compensator.
A second solution of using a medium scale power
converter with a wounded rotor induction generator is
shown in Fig. 33b [18]-[26]. Slip-rings are making the
electrical connection to the rotor. A power converter
controls the rotor currents. If the generator is running super-
synchronously electrical power is delivered through both the
rotor and the stator. If the generator is running sub-
synchronously electrical power is only delivered into the
rotor from the grid. A speed variation of ±30 % around
synchronous speed can be obtained by the use of a power
converter of 30 % of nominal power.

Gear

Induction

generato

Active

Stall

Grid

Reactive

pensator

III

Furthermore, it is possible to control both active (P

ref

) and

reactive power (Q

ref

), which gives a better grid performance,

and the power electronics enable the wind turbine to act
more as a dynamic power source to the grid. The solution
shown in Fig. 33b needs neither a soft-starter nor a reactive
power compensator. The solution is naturally a little bit
more expensive compared to the classical solutions shown
in Fig. 32 and Fig. 33a. However, it is possible to save
money on the safety margin of gear, reactive power
compensation units and it is possible to capture more energy
from the wind.

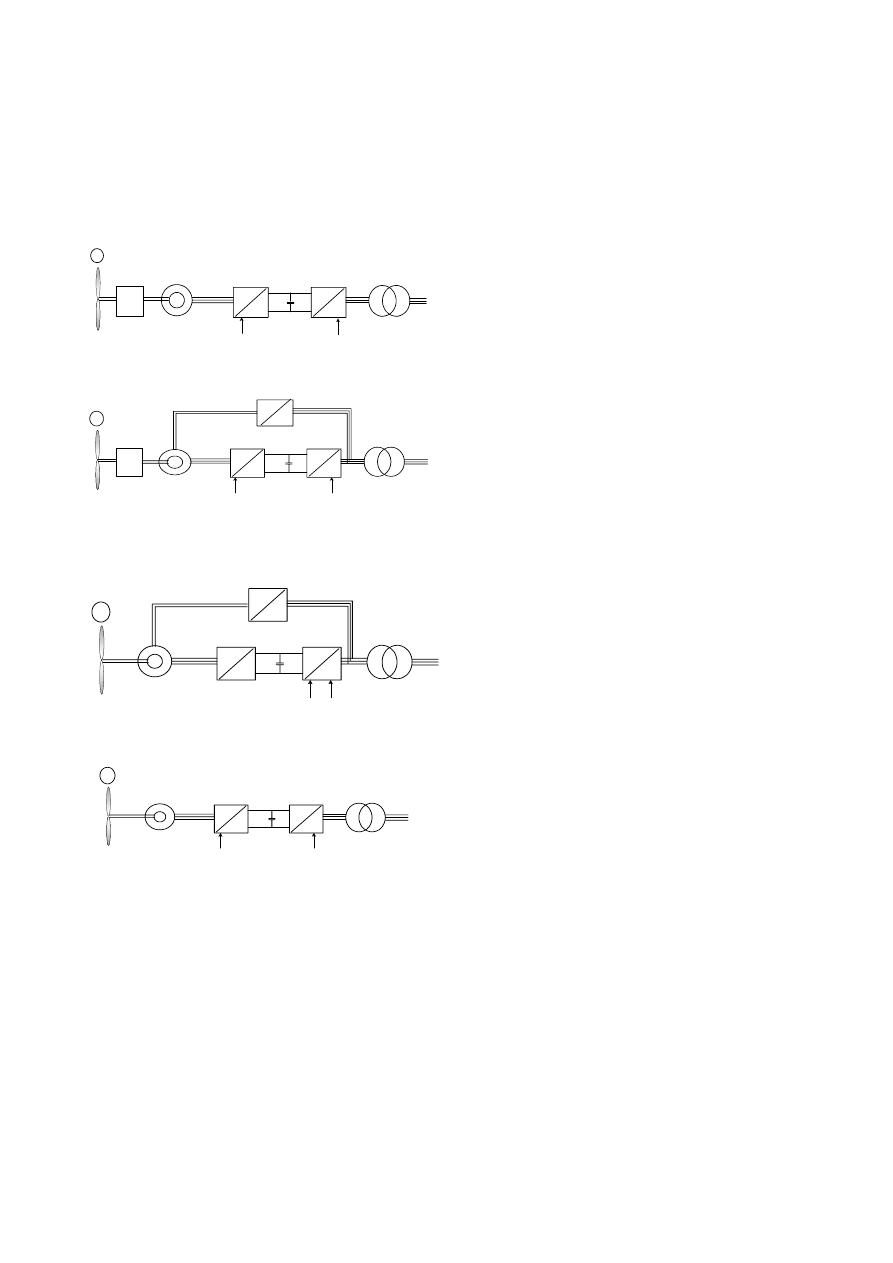
The wind turbines with a full-scale power converter
between the generator and grid give extra losses in the
power conversion but it may be gained by the added
technical performance [9]. Fig. 34 shows four possible
solutions with full-scale power converters.

(a)

(b)

(c)

P M-synchronous

G enerator

Multi-pole

P itch

G rid

D C

AC

AC

D C

P

ref

Q

ref

IX

(d)

Fig. 34. Wind turbine systems with full-scale power converters.
a) Induction generator with gear (System VI)
b) Synchronous generator with gear (System VII)
c)

Multi-pole synchronous generator (System VIII)

d)

Multi-pole permanent magnet synchronous generator (System IX).

The solutions shown in Fig. 34a and Fig. 34b are
characterized by having a gear. A synchronous generator
solution shown in Fig. 34b needs a small power converter
for field excitation. Multi-pole systems with the
synchronous generator without a gear are shown in Fig. 34c
and Fig. 34d.
The last solution uses permanent magnets, which are still
becoming cheaper and thereby more attractive. All four
solutions have the same controllable characteristics since the
generator is decoupled from the grid by a dc-link. The

power converter to the grid enables the system very fast to
control active and reactive power. However, the negative
side is a more complex system with a more sensitive
electronic part.
By introducing power electronics many of the wind
turbine systems get a performance like a power plant. In
respect to control performance they are faster but of course
the produced real power depends on the available wind. The
reactive power can in some solutions be delivered without
having any wind.

Gear

Induction

generator

Pitch

Grid

DC

AC

AC

DC

P

ref

Q

ref

VI

Fig. 34 also indicates other important issues for wind
turbines in order to act as a real power source for the grid.
They are able to be active when a fault appears at the grid
and so as to build the grid voltage up again quickly; the
systems have the possibility to lower the power production
even though more power is available in the wind and
thereby acting as a rolling capacity. Finally, some are able to
operate in island operation in the case of a grid collapse.

P itc h

V I I

G e a r

S y n c h r o n o u s

G e n e r a to r

G rid

D C

A C

A C

D C

P

r e f

Q

re f

D C

A C

VII.

C

ONTROL OF

W

IND

T

URBINES

Controlling a wind turbine involves both fast and slow

control. Overall the power has to be controlled by means of
the aerodynamic system and has to react based on a set-
point given by dispatched center or locally with the goal to
maximize the production based on the available wind power.
The power control system should also be able to limit the
power. An example of an overall control scheme of a wind
turbine with a doubly-fed generator system is shown in Fig.
35.

Grid

P

ref

Q

ref

Synchronous

Generator

Multi-pole

Pitch

DC

AC

AC

DC

VIII

DC

AC

Below maximum power production the wind turbine will
typically vary the speed proportional with the wind speed
and keep the pitch angle

θ fixed. At very low wind the speed

of the turbine will be fixed at the maximum allowable slip in
order not to have overvoltage.
A pitch angle controller will limit the power when the
turbine reaches nominal power. The generated electrical
power is done by controlling the doubly-fed generator
through the rotor-side converter. The control of the grid-side
converter is simply just keeping the dc-link voltage fixed.
Internal current loops in both converters are used which
typically are linear PI-controllers, as it is illustrated in Fig.
36a. The power converters to the grid-side and the rotor-side
are voltage source inverters.
Another solution for the electrical power control is to use
the multi-pole synchronous generator. A passive rectifier
and a boost converter are used to boost the voltage at low
speed. The system is industrially used today. It is possible to
control the active power from the generator. The topology is
shown in Fig. 36b. A grid inverter is interfacing the dc-link
to the grid. Here it is also possible to control the reactive
power to the grid. Common for both systems are they are
able to control reactive and active power very fast and
thereby the turbine can take active part in the power system
control.

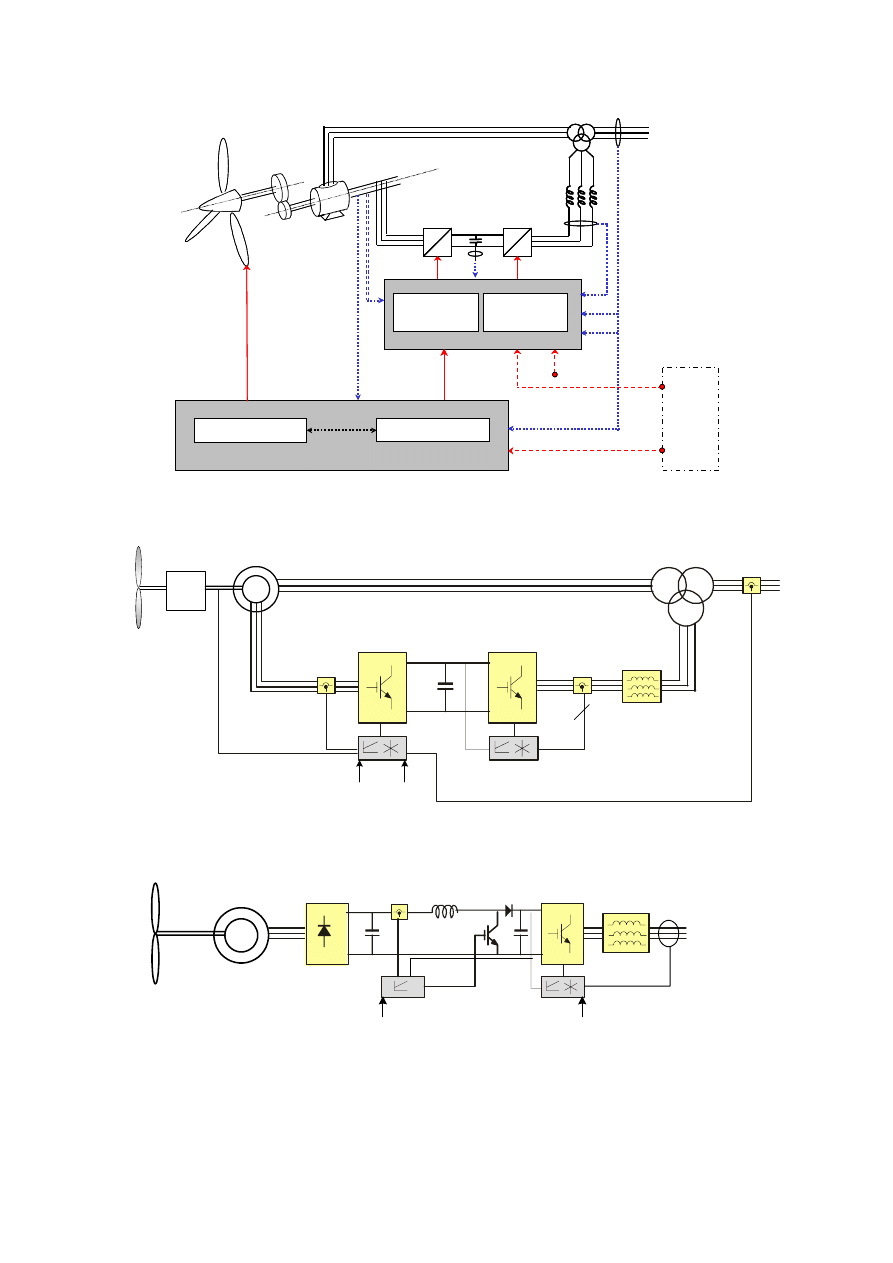
dd

DFIG control

Power

controller

Speed controller

Wind turbine

control

Rotor side

converter controller

Grid side

converter controller

Measurement

grid point M

θ

AC

DC

AC

DC

meas
gen

ω

PWM

PWM

N

T

ref

conv

gri

P

,

ref

conv

grid

Q

,

meas

dc

U

meas

grid

P

meas

grid

P

meas

grid

Q

meas

ac

I

ref

dc

U

ref

rated

grid

P

,

cross

-

coupling

Grid

operators

control

system

meas

rotor

I

DFIG control

Power

controller

Power

controller

Speed controller

Speed controller

Wind turbine

control

Rotor side

converter controller

Rotor side

converter controller

Grid side

converter controller

Measurement

grid point M

θ

AC

DC

AC

DC

meas
gen

ω

PWM

N

T

ref

conv

gri

P

,

ref

conv

grid

Q

,

meas

dc

U

meas

grid

P

meas

grid

P

meas

grid

Q

ac

I

ref

dc

U

ref

rated

grid

P

,

cross

-

coupling

Grid

operators

control

system

meas

rotor

I

Fig. 35. Control of wind turbine with doubly-fed induction generator system [35 ].

Grid

v

DC

P
Q

v

ra,

rb,

rc

i

ra, rb, rc

Rotor

control

Rotor-side

converter

Grid-side

converter

Inductance

Grid

control

DFIG

Transformer

θ

r

grid

grid

ref

ref

P

Q

Gear

v v

i i

3

v

ga, gb, gc

i

ga, gb, gc

v v

i i

(a)

v

DC

v

DC

Generator

rectifier

Grid

inverter

Inductance

Grid

control

Power

control

PMG

Grid

ref

Q

ref

P

v

ga, gb, gc

i

ga, gb, gc

v v

i i

(b)

Fig. 36. Basic control of active and reactive power in a wind turbine [11].

a) Doubly-fed induction generator system (System V)

b) Multi-pole synchronous generator system (System VIII)

VIII. C

ONCLUSION

This paper has described three important renewable energy
sources: Wind turbines, photovoltaic and fuel cell. Power
converters both for single-phase and three-phase inter-
connection is described and means to control the power
converter are discussed.
The system will in the future be able to contribute the grid
control using active and reactive power control, which is
enabled by power electronics. The renewable energy will
play a major role in the future power system.

R

EFERENCES

[1] J.F. Manwell, J. G. McGowan, A. L. Rogers, Wind Energy Explained,

Theory, Design and Application. Wiley, 1998.

[2] S. Heier. Grid integration of wind energy conversion

systems/translated by Rachel Waddington. John Wiley, 1998.

[3] T. Burton, D. Sharpe, N. Jenkins, E. Bossanyi. Wind Energy

Handbook. John Wiley, 2000.

[4] P. Thoegersen, F. Blaabjerg. “Adjustable Speed Drives in the Next

Decade. Future Steps in Industry and Academia”. Journal of Electric
Power Components and Systems, Vol. 32, No. 1, 2004, pp. 13-32.

[5] B.J. Baliga, “Power IC’s in the saddle”, IEEE Spectrum, July 1995,

pp. 34-49.

[6] F. Blaabjerg, Z. Chen, “Power Electronics as an enabling technology

for Renewable Energy Integration”, Journal of Power Electronics, Vol.
3, No. 2, April 2003, pp. 81-89.

[7] F. Blaabjerg, Z. Chen, S.B. Kjaer, “Power Electronics as Efficient

Interface in Dispersed Power Generation Systems”, IEEE Trans. on
Power Electronics, Vol. 19, No. 4, 2004, pp. 1184-1194.

[8] O. Carlson, J. Hylander, K. Thorborg, “Survey of variable speed

operation of wind turbines”, Proc. of European Union Wind Energy
conference, Sweden, 1996, pp.406-409.

[9] M.R. Dubois, H. Polinder, J.A. Fereira, J.A, “Comparison of

Generator Topologies for Direct-Drive Wind Turbines”, IEEE Nordic
Workshop on Power and Industrial Electronics, NORPIE 2000, 2000,
pp. 22-26.

[10] L.H. Hansen, L. Helle, F. Blaabjerg, E. Ritchie, S. Munk-Nielsen, H.

Bindner, P. Sørensen, B. Bak-Jensen, “Conceptual survey of
Generators and Power Electronics for Wind Turbines”, 2001, Risø-R-
1205 (EN).

[11] M.P. Kazmierkowski, R. Krishnan, F. Blaabjerg. Control in Power

Electronics Selected problems. Academic Press, 2002.

[12] Z. Chen, E. Spooner, ”Wind turbine power converters: a comparative

study”, Proc. of Power Electronics and Variable Speed Drives, 1998,
pp. 471 – 476.

[13] L.H. Hansen, P.H. Madsen, F. Blaabjerg, H.C. Christensen, U.

Lindhard, K. Eskildsen, “Generators and power electronics
technology for wind turbines”, Proc. of IECON '01, Vol. 3, 2001, pp.
2000 – 2005.

[14] J. Rodriguez, L. Moran, A. Gonzalez, C. Silva, “High voltage

multilevel converter with regeneration capability”, Proc. of PESC ‘99,
1999, Vol.2, pp.1077-1082.

[15] E.N. Hinrichsen, “Controls for variable pitch wind turbine generators”,

IEEE Trans. On Power Apparatus and Systems, Vol. 103, No. 4, 1984,
pp. 886-892.

[16] T. A. Lipo, “Variable Speed Generator Technology Options for Wind

Turbine Generators”, NASA.Workshop on HAWTT Technology,
May 1984, pp. 214-220.

[17] Z. Chen, E. Spooner, “Grid Interface Options for Variable-Speed,

Permanent-Magnet Generators”, IEE Proc. -Electr. Power
Applications, Vol. 145, No. 4, July 1998, pp. 273-283.

[18] J.D. van Wyk, J.H.R. Enslin, “A Study of Wind Power Converter

with Microcomputer Based Maximal Power Control Utilising an
Oversynchronous Electronic Schertives Cascade”, Proc. of IPEC '83,
Vol. I, 1983, pp. 766-777.

[19] D. Arsudis, W. Vollstedt, “Sensorless Power control of a Double-Fed

AC-Machine with nearly Sinusoidal Line Currents”, Proc. of EPE '89,
Aachen 1989, pp. 899-904.

[20] D. Arsudis, “Doppeltgespeister Drehstromgenerator mit

Spannungszwischenkreis Umrichter in Rotorkreis für Wind
Kraftanlagen, Ph.D. Thesis, 1998, T.U. Braunschweig, Germany.

[21] D. Arsudis, “Sensorlose Regelung einer doppelt-gespeisten

Asynchronmaschine mit geringen Netzrückwirkungen“, Archiv für
Elektrotechnik, Vol. 74, 1990, pp. 89-97.

[22] S. Bhowmik, R. Spee, J.H.R. Enslin, “Performance optimization for

doubly fed wind power generation systems”, IEEE Transactions on
Industry Applications, Vol. 35, No. 4 , July-Aug. 1999, pp. 949 – 958.

[23] J.B. Ekanayake, L. Holdsworth, W. XueGuang, N. Jenkins, “Dynamic

modelling of doubly fed induction generator wind turbines”, Trans. on
Power Systems, Vol. 18, No. 2, May 2003, pp. 803- 809.

[24] Yamamoto, O. Motoyoshi, “Active and Reactive Power control for

Doubly-Fed Wound Rotor Induction Generator”, Proc. of PESC '90,
Vol. 1, pp. 455-460.

[25] E. Bogalecka, “Power control of a doubly fed induction generator

without speed or position sensor”, Proc. of EPE’93, Vol. 8, pp. 224-
228, 1993.

[26] R. Pena, J.C. Clare, G.M. Asher, “Doubly fed induction generator

using back-to-back PWM converters and its application to variable
speed wind-energy generation”. IEE Proc. on electric power
application, 1996, pp. 231-241.

[27] Z. Chen, E. Spooner, “Voltage Source Inverters for High-Power,

Variable-Voltage DC Power Sources”, IEE Proc. –Generation,
Transmission and Distributions, Vol. 148, No. 5, September 2001, pp.
439-447.

[28] M. Dahlgren, H. Frank, M. Leijon, F. Owman, L. Walfridsson, “Wind

power goes large scale”, ABB Review, 2000, Vol.3, pp. 31-37.

[29] A.K. Wallace, J.A. Oliver, “Variable-Speed Generation Controlled by

Passive Elements”, Proc. of ICEM ’98, Vol. 3, 1998, pp. 1554-1559.

[30] Z. Chen, E. Spooner, “Grid Power Quality with Variable-Speed Wind

Turbines”, IEEE Transactions on Energy Conversion, Vol. 16, No.2,
June 2001, pp. 148-154.

[31] S. Bolik, “Grid Requirements Challenges for Wind Turbines”, Proc.

of Fourth International Workshop on Large-Scale Integration of Wind
Power and Transmission Networks for Offshore Windfarms, 2003.

[32] L. Mihet-Popa, F. Blaabjerg, I. Boldea, “Wind Turbine Generator

Modeling and Simulation where Rotational Speed is the controlled
Variable”, IEEE Trans. on Industry Applications, Vol. 40, No. 1, pp.
3-10, Jan/Feb. 2004.

[33] F. Iov, F. Blaabjerg, A.D. Hansen, “Analysis of a variable-speed

wind energy conversion scheme with doubly-fed induction
generator”, Int. Journal of Electronics, 2003, Vol. 90, No. 11-12, pp.
779-794.

[34] R. Teodorescu, F. Blaabjerg, “ Flexible Control of Small Wind

Turbines with Grid Failure Detection Operating in Stand-Alone and
Grid-Connected Mode”, IEEE Trans. on Power Electronics, Vol. 19,
No. 5, 2004, pp. 1323-1332.

[35] C. Jauch, A.D. Hansen, P. Soerensen, F. Blaabjerg, “ Simulation

Model of an Actove-stall Fixed-speed Win Turbine Controller ” ,
Journal of Wind Engineering, Vol. 28, No. 2, 2004, pp. 177-195.

[36] A.D. Hansen, F. Iov, F. Blaabjerg, L.H. Hansen, “ Review of

Contemporary Wind Turbine Concepts and their Market
Penetration”, Journal of Wind Engineering, Vol. 28, No. 3, 2004, pp.
247-263.

[37] R. Teodorescu, F. Blaabjerg, M.Liserre, “Stability of Grid-Connected

PV Inverters with Large Grid Impedance Variation”, Proc. of
PESC’04, 2004, pp. 4773-4779.

[38] T. Shimizu, M. Hirakata, T. Kamezawa, H. Watanabe, “Generation

Control Circuit for Photovoltaic Modules“ IEEE Trans. On Power
Electronics, Vol. 16, No. 3, May, 2001, pp. 293 – 300.

[39] M. Calais, J. Myrzik, T. Spooner, V.G. Agelidis, “Inverters for

single-phase grid connected photovoltaic systems-an overview”, Proc.
of PESC ’02, 2002, Vol. 4, pp. 1995 – 2000.

[40] K. Ogura, T. Nishida, E. Hiraki, M. Nakaoka and S. Nagai, “Time-

Sharing Boost Chopper Cascaded Dual Mode Single-Phase Sinewave
Inverter for Solar Photovoltaic Power Generation System”, Proc. of
PESC’04, 2004, pp. 4763-4766.

[41] M. Calais, V.G. Agelidis, L.J. Borle, M.S. Dymond, “A

transformerless five level cascaded inverter based single phase
photovoltaic system”, Proc. of PESC’00, 2000, Vol. 3, pp. 1173-
1178.

[42] H.Haeberlin, “Evolution of Inverters for Grid connected PV systems

from 1989 to 2000“, Proc. of Photovoltaic Solar Energy Conference,
2001.

[43] R. Teodorescu, F. Blaabjerg, M. Liserre, U. Borup, ” A New Control

Structure for Grid-Connected PV Inverters with Zero Steady-State
Error and Selective Harmonic Compensation”, Proc. of APEC’04, ,
Vol. 1, 2004, pp. 580-586.

[44] J. H. R. Enslin and P. J. M. Heskes, “Harmonic interaction between a

large number of distributed power inverters and the distributed
network”, Proc. of PESC ‘03, 2003, pp. 1742-1747.

[45] D.P. Hohm, M.E. Ropp, “Comparative study of maximum power

point tracking algorithms using an experimental, programmable,
maximum power point tracking test bed”, Proc. of Photovoltaic
Specialists Conference, 2000, pp.1699 – 1702.

[46] European Standard EN 50330-1, Photovoltaic semiconductor

converters Part 1: Utility interactive fail safe protective interface for
PV-line commutated converters - Design qualification and type
approval, 1999.

[47] M. Sumner, B. Palethorpe, D.W.P. Thomas, P. Zanchetta, M.C.Di

Piazza, "A technique for power supply harmonic impedance
estimation using a controlled voltage disturbance", IEEE Trans. on
Power Electronics, Vol. 17, No. 2, 2002, pp. 207 – 215.

[48] L. Asiminoei, R. Teodorescu, F. Blaabjerg, U. Borup, ”A new method

of on-line grid impedance estimation for PV inverters”, Proc. of
APEC’04, Vol. 3, 2004, pp. 1527-1533.

[49] A. Timbus, R. Teodorescu, F. Blaabjerg, U. Borup. ”Online Grid

measurement and ENS detection for PV inverters running on highly
inductive grid” – IEEE Power Electronic Letters (in press).

[50] M. Liserre, A. Dell’Aquila and F. Blaabjerg, “Genetic algorithm

based design of the active damping for a LCL-filter three-phase active
rectifier,” IEEE Trans. on Power Electronics, Vol. 19, pp. 76 -86, Jan.
2004.

[51] V. Blasko and V. Kaura, “A novel control to actively damp resonance

in input LC filter of a three-phase voltage source converter”, IEEE
Trans. on Ind. App., vol. 33, 1997, pp. 542-550.

[52] P. A. Dahono, “A control method to damp oscillation in the input LC

filter of AC-DC PWM converters”, Proc. of PESC 2002, June 2002,
pp. 1630-1635.

[53] P. C. Loh, M. J. Newman, D.N. Zmood, D.G. Holmes, “A

Comparative Anlysis of multiloop Voltage Regulation Strategies for
Single and Three-Phase UPS Systems”, IEEE Trans. on Power
Electronics, Vol. 18, No. 5. Sept. 2003, pp. 1176-1185.

[54] T. Ohnishi, “Three phase PWM converter/inverter by means of

instantaneous active and reactive power control”, Proc. of IECON 91,
Vol. 2, 1991, pp. 819-824.

[55] T. Noguchi, H. Tomiki, S. Kondo, I. Takahashi, “Direct power

control of PWM converter without power-source voltage sensors”,
IEEE Trans. on Ind. App., vol. 34, May/June 1998, pp. 473-479.

[56] I. Agirman and V. Blasko, “A novel control method of a VSC without

AC line voltage sensors”, IEEE Trans. on Ind. App., Vol. 39,
March/April 2003, pp.519-524.

[57] M. Liserre A. Dell’Aquila, F. Blaabjerg. “Design and control of a

three-phase active rectifier under non-ideal operating conditions” in
Proc. of IAS ‘02, 2002, pp. 1181-1188.

[58] A. Moran, P. D. Ziogas, G. Joos: “Design aspects of synchronous

PWM rectifier-inverter system under unbalanced input voltage
conditions”, IEEE Trans. on Ind. App., vol. 28, Nov./Dec. 1992, pp.
1286-1293.

[59] M. Liserre, F. Blaabjerg, S. Hansen: “Design and Control of an LCL-

filter Based Active Rectifier”, Proc. of IAS’01, 2001, Vol. 1, pp. 299-
307.

[60] N. Mohan, T. Undeland, W.P. Robbins, “Power Electronics.

Converters, Applications and Design”. John Wiley & Sons 2003,
ISBN: 0-471-22693-9

[61] R.W. Erickson, D. Maksimovic, “Fundamentals of Power

Electronics”, Kluwer Academic Pub; March 1, 1997, ISBN: 0-412-
08541-0, 773 pages.

[62] C. Cecati, A. Dell'Aquila, M. Liserre and V. G. Monopoli, "Design of

H-bridge multilevel active rectifier for traction systems", IEEE Trans.
on Ind. App., Vol. 39, Sept./Oct. 2003, pp. 1541-1550.

[63] X. Yuan, W. Merk, H. Stemmler, J. Allmeling, “Stationary-Frame

Generalized Integrators for Current Control of Active Power Filters
with Zero Steady-State Error for Current Harmonics of Concern

Under Unbalanced and Distorted Operating Conditions” IEEE Trans.
on Ind. App., Vol. 38, No. 2, Mar./Apr. 2002, pp. 523 – 532.

[64] P. Mattavelli, “A Closed-Loop Selective Harmonic Compensation for

Active Filters”, IEEE Trans. on Ind. App., Vol. 37, No. 1,
January/February, 2001, pp. 81 – 89.

[65] D. N. Zmood, D. G. Holmes, “Stationary Frame Current Regulation

of PWM Inverters with Zero Steady-State Error”, IEEE Trans. on
Power Electronics, Vol. 18, No. 3, May 2003, pp. 814 – 822.

[66] B.K. Bose, Modern Power Electronics and A.C. Drives, 1st ed.,

Prentice Hall, 2001, ISBN 0-13-016743.

[67] R.O. Caceres and I. Barbi, “A boost DC-AC converter: analysis,

design, and experimentation” IEEE Transactions on Power
Electronics, Vol. 14, No. 1, January, 1999, pp. 134-141.

[68] C. Cecati, A. Dell’Aquila, M. Liserre, “A Novel Three-Phase Single-

Stage Distributed Power Inverter”, IEEE Transactions on Power
Electronics, Vol. 19, No. 5, September, 2004, pp. 1226-1233.