Wojskowa Akademia Techniczna
im. Jarosława Dąbrowskiego
Obliczenia rozproszone i równoległe.
Temat sprawozdania: Obliczanie macierzy
odwrotnej.
Prowadzący: mgr Adam Misztak
Wykonał: st. szer. pchor. Piotr Jakubowski
Grupa: I8C1S1
1 Pojęcie macierzy
Macierz odwrotna jest to element odwrotny w pierścieniu macierzy kwadratowych.
Uogólnieniem pojęcia macierzy odwrotnej jest tzw. uogólniona macierz odwrotna.
2 Przykład wyznaczania macierzy z definicji.
Z definicji. A
-1
=
A
det
1
(
A )
T
gdzie Ā – macierz dopełnień algebraicznych o wyznaczniku detA
0
3. Przykład
A =
3
2
5
4
3
6
7
5
2
Rozwiązanie:
det(A) =
3
2
5
4
3
6
7
5
2
2
3
5
5
6
2
= -18 + 100 – 84 – 105 + 16 +90, czyli det(A) = -1
0,
więc A
-1
istnieje.
Teraz obliczamy dopełnienia algebraiczne wszystkich wyrazów macierzy A:
d
11
= (-1)
1+1
3
2
4
3
= -9 + 8 = -1, d
12
= (-1)
1+2
3
5
4
6
= -(-18-20) = 38
d
13
= (-1)
1+3
2
5
3
6
= -12 - 15 = -27,
d
21
= (-1)
2+1
3
2
7
5
= -(-15 + 14) = 1, d
22
= (-1)
2+2
3
5
7
2
= - 6 - 35 = -41,
d
23
= (-1)
2+3
2
5
5
2
= -( - 4 - 25) = 29,
d
31
= (-1)
3+1
4
3
7
5
= 20 - 21 = -1, d
32
= (-1)
3+2
4
6
7
2
= - (8 – 42) = -34,
d
33
= (-1)
3+3
3
6
5
2
= 6 - 30) = -24,
Tworzymy macierz dopełnieo
D =
24
34
1
29
41
1
27
38
1
Zatem A
-1
= 1
)
det(
1
A
D
T
=
= (-1)
24
29
27
34
41
38
1
1
1
, czyli ostatecznie A
-1
24
29
27
34
41
38
1
1
1
.
4. Zadanie laboratoryjne.
W zadaniu zakładam, że macierz odwrotną da się wyznaczyć oraz pomijam sprawdzenie
detA
0
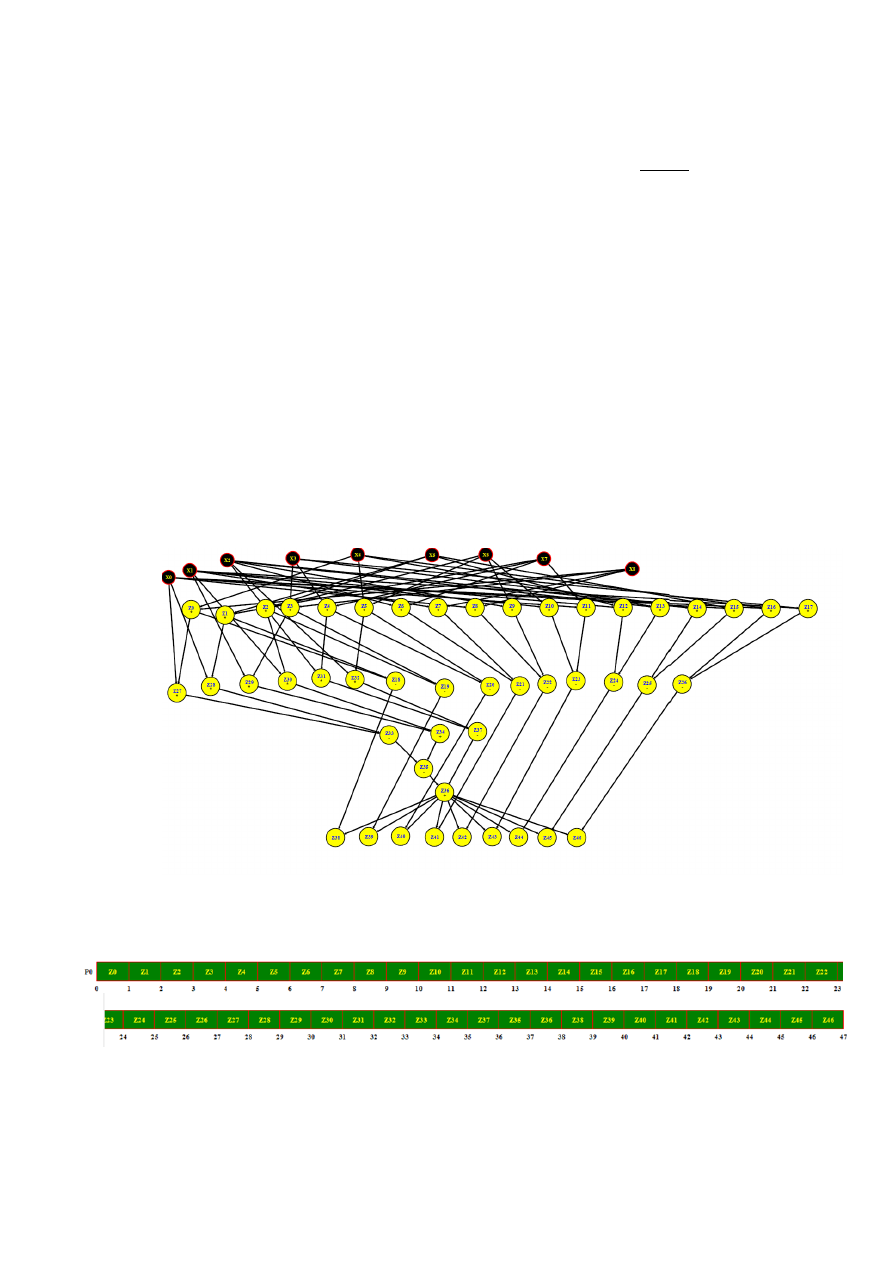
Graf obliczający wyznacznik macierzy dopełnień oraz proces odwracania macierzy
Utworzony harmonogram dla:
p=1
p – procesor
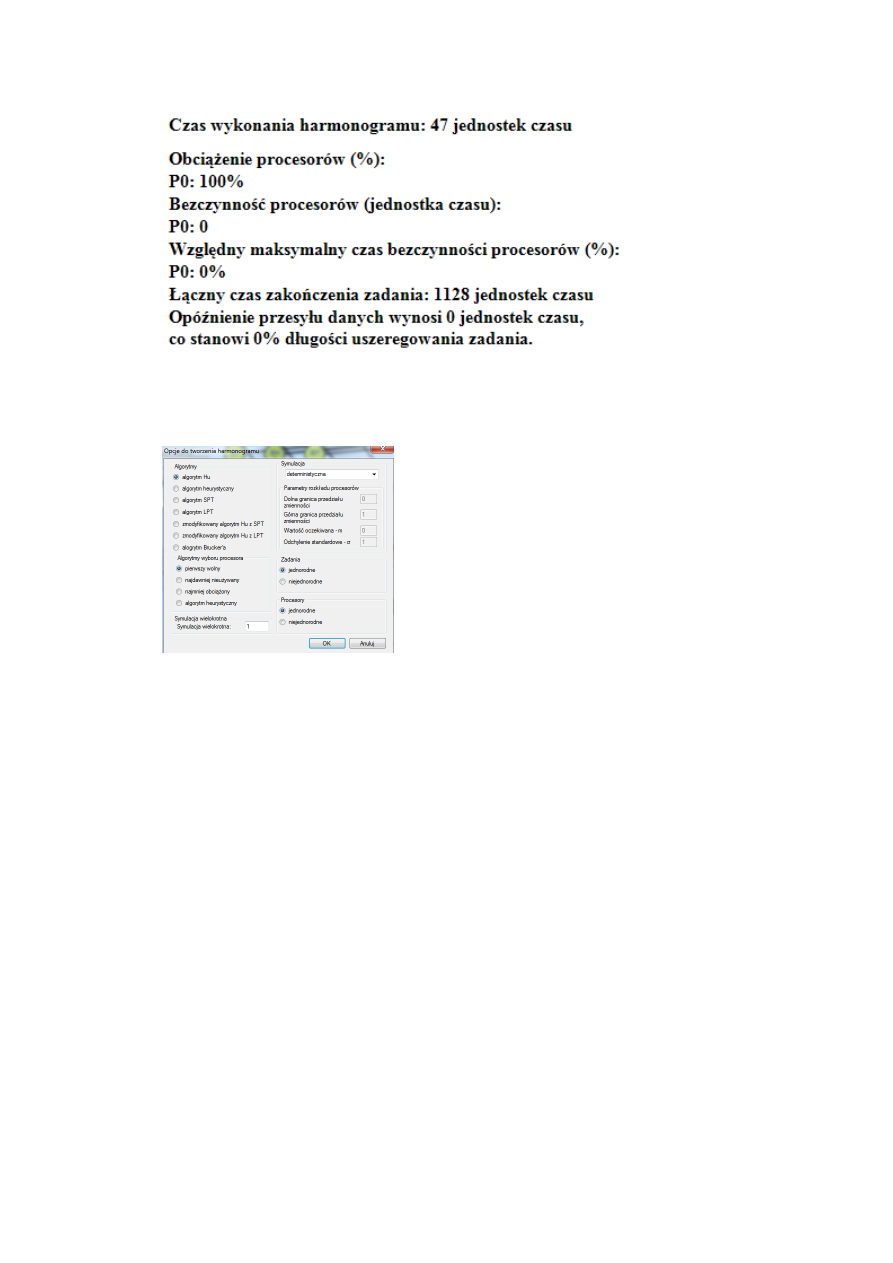
Warunki:
oszacowad teoretyczną złożonośd obliczeniową problemu, jako funkcję rozmiaru zadania
algorytmu sekwencyjnego.
Algorytm sekwencyjnym dla macierzy n
x
n, gdzie n=3, wykonuję:
–
24 operacje mnożenia
–
14 operacji odejmowania lub dodawania
–
9 operacji dzielenia
Należy wykonad 2*n^2+2n operacji mnożenia, n^2+n+2 operacji dodawania lub
odejmowania oraz n^2 operacji dzielenia.
Złożonośd dla n=3 można wyrazid wzorem:
5*n^2+2, więc jest rzędu O(n^2)
Jednak dla większych n złożonośd ta będzie inna, gdyż zmienia się sposób liczenia
wyznacznika dla podmacierzy, złożonośd opisuje wzór:
2*n^4-4*n^3+3^2+5n-3.
5.
Złożoność dla m procesorów.
Funkcja zależności złożoności od liczby procesorów i wielkości zadania jest następująca:
[45/p]+3
dla n=3
(2*n^4-4*n^3+3^2+5n)/p-3 ,gdzie:
[ ] - sufit z liczby
p – liczba procesorów
n – rozmiar macierzy
Poniżej harmonogramy dla wielu procesorów:
P=2
Dla p = 3
Dla p = 6
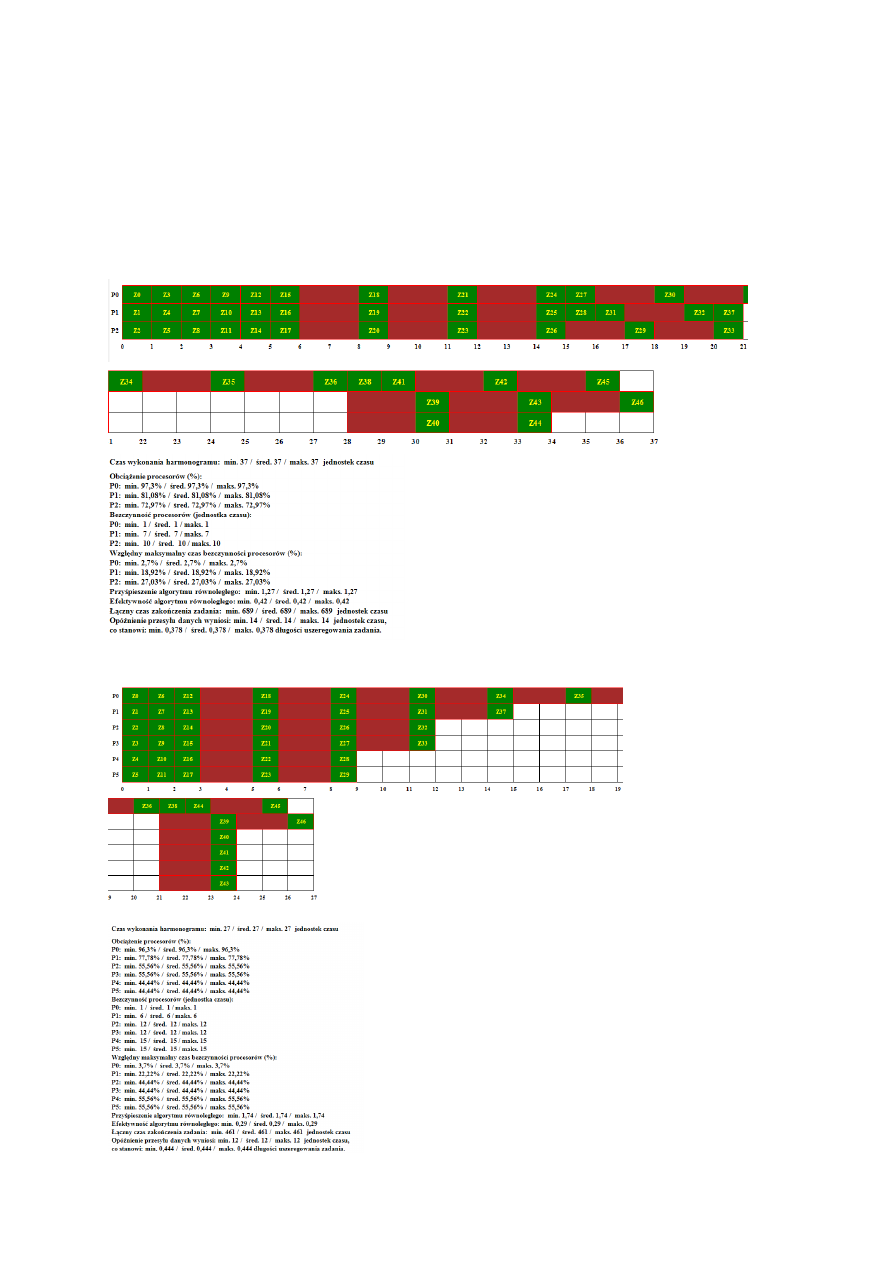
6. Procesory połączone są w sieci każdy – z - każdym , opóźnienia
przesyłu danych między procesorami są równe 2 oraz opóźnienia
przesyłu danych wewnątrz każdego procesora są równe 1.
Dla p = 3
Dla p = 6
Dla p = 9
7. procesory jednorodne i niejednorodne(każdy kolejny jest
dwukrotnie szybszy od poprzedniego)
Dla
p = 2 procesory jednorodne 2 (liczba procesorów mniejsza od rozmiaru zadania)
p=2 procesory niejednorodne:
Dla p = 18
Dla p=18 procesory niejednorodne:
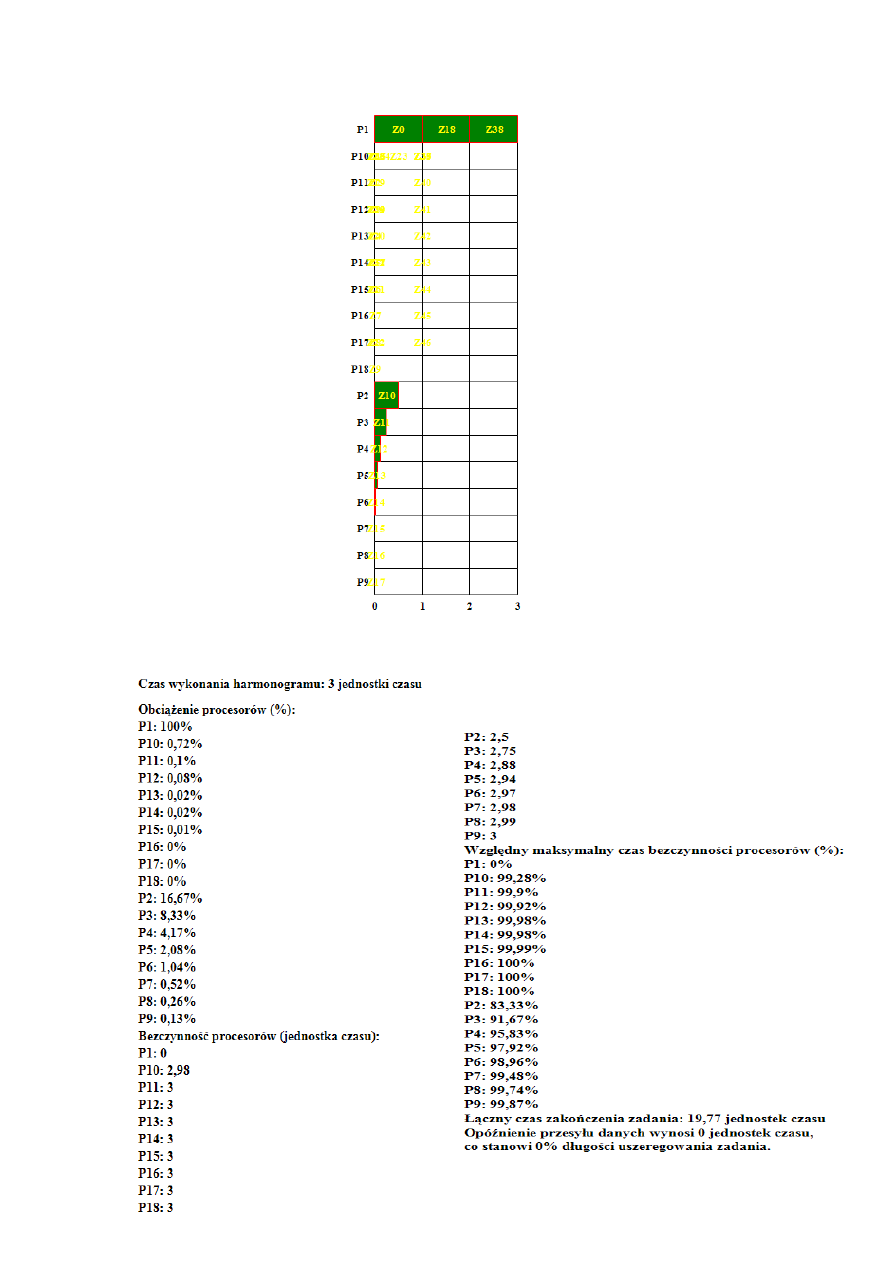
8. Działania niejednorodne i jednorodne.
Dla p=2 dla działao jednorodnych,
Dla p =2, czas dodawania=1, czas odejmowania=1, dzielenia=3, mnożenia=2
Dla p=18 dla działao jednorodnych,
Dla p=18 czas dodawania=1, czas odejmowania=1, dzielenia=3, mnożenia=2
9 Podsumowanie
Zadanie wykonałem zgodnie z wytycznym. Rozwiązałem zadanie na podstawie definicji
odwracania macierzy. W rozwiązaniu założyłem, że detA
0 i zadanie jest możliwe do
rozwiązania. Zadanie uważam, za trudne ponieważ jest wiele możliwości jego rozwiązania.
Przy macierzy 4*4 lub 6*6 tych założeo oraz zmiennych trzeba byłoby więcej, a co za tym
idzie sposób rozwiązania musiałby byd trochę inny. Efektywnośd zadania spada przy
zastosowaniu większej ilości procesorów ponieważ procesory są bezczynne, gdyż czekają na
wykonanie czynności przez procesory aktywne. Zdecydowanie najlepszy wynik czasowy to 3
jednostki przy 18 procesorach niejednorodnych. Potwierdza to wspomniany fakt, że 18 jest
liczbą procesorów powyżej której czas już się nie zmniejszy. Jednak taki przebieg został
wykonany ogromnym nakładem sprzętowym, gdyż każdy procesor był dwukrotnie szybszy od
poprzedniego. Najwolniej rozwiązało się zadanie przy użyciu opróżnieo przesyłu danych
między procesorami oraz poprzez procesor. Im większy czas opróżnienia tym dłuższy czas
wykonania zadania, nawet przy procesorach niejednorodnych gdy ustawiłem w działaniach
operacji (czasy operacji takie jak: dodawanie, odejmowanie, dzielenie i mnożenie) nie działały
szybciej od tych bez opóźnieo.