120

MECHANIK NR 2/2011

* Mgr inż. Krzysztof Damaziak, dr inż. Jerzy Małachowski – Kate-

dra Mechaniki i Informatyki Stosowanej, Wydział Mechaniczny Woj-
skowej Akademii Technicznej, mgr inż. Paweł Płatek, dr inż. Ryszard
Woźniak – Instytut Techniki Uzbrojenia, Wydział Mechatroniki Woj-
skowej Akademii Technicznej

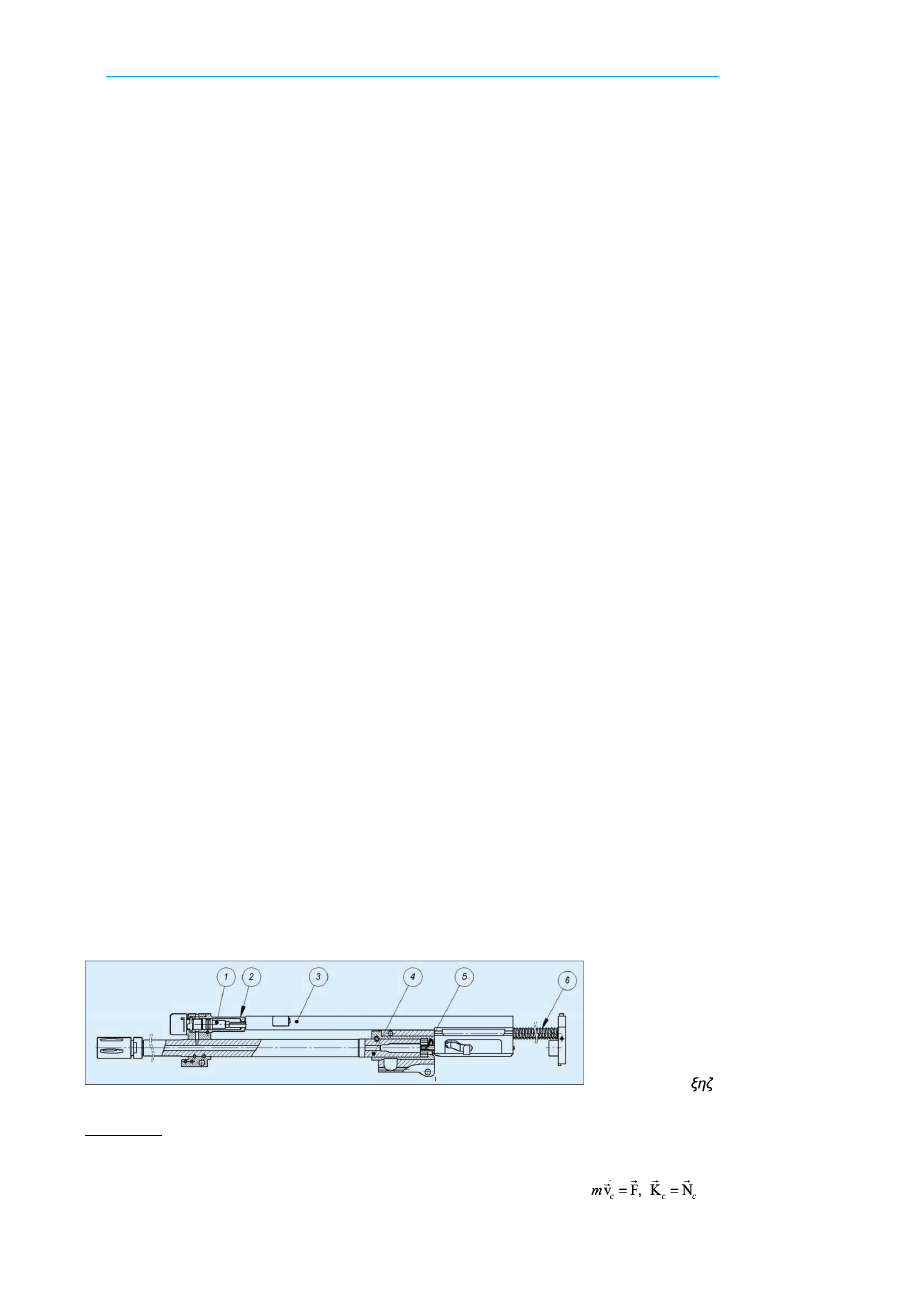
Rys. 1. Widok ogólny analizowanego układu:

1 – tłok gazowy, 2 – wkładka komory gazowej,

3 – suwadło, 4 – obsada lufy, 5 – zamek, 6 – mechanizm powrotny

Analiza możliwości wykorzystania różnych metod numerycznych

w procesie projektowania układu automatyki broni strzeleckiej

kalibru 5,56 mm

KRZYSZTOF DAMAZIAK

JERZY MAŁACHOWSKI

PAWEŁ PŁATEK

RYSZARD WOŹNIAK *

Zakład Konstrukcji Specjalnych w Instytucie Techniki
Uzbrojenia, Wydziału Mechatroniki WAT realizuje od
2007 r., we współpracy z Fabryką Broni „Łucznik”-Ra-
dom, projekt rozwojowy, którego celem jest zaprojek-
towanie, wykonanie i przebadanie dwóch demonstratorów
technologii karabinków podstawowych kalibru 5,56 mm
zbudowanych w klasycznym kolbowym oraz bezkolbo-
wym układzie konstrukcyjnym. W artykule przedstawiono
możliwości wykorzystania dwóch metod numerycznych
w procesie określania charakterystyk dynamicznych wy-
branych elementów składowych automatyki karabinka.

Powstające w ramach projektu karabinki charakteryzu-

ją się wieloma innowacyjnymi rozwiązaniami, które do-
tychczas nie były stosowane w fabryce z Radomia. Jedno
z nich dotyczy sposobu funkcjonowania automatyki kara-
binka, która działa na zasadzie odprowadzania części
gazów prochowych przez boczny otwór w lufie, z wyko-
rzystaniem krótkiego ruchu tłoka gazowego [1]. Aby prze-
analizować wpływ nowego rozwiązania konstrukcyjnego
na poprawność działania zespołu automatyki karabinków,
przeprowadzono cykl badań numerycznych, których wy-
niki zweryfikowano doświadczalnym strzelaniem. Symu-
lacje komputerowe prowadzono z wykorzystaniem ap-
likacji wspomagających proces obliczeń inżynierskich,
bazujących na dwóch metodach numerycznych: Meto-
dzie Układów Wieloczłonowych oraz Metodzie Elemen-
tów Skończonych.

Charakterystyka automatyki broni
z krótkim ruchem tłoka gazowego

Nowo projektowane karabinki podstawowe MSBS-5,56

działają na zasadzie odprowadzenia części gazów pro-
chowych przez boczny otwór w lufie z wykorzystaniem
krótkiego ruchu tłoka gazowego.

W

zaproponowanym

rozwiązaniu

konstrukcyjnym

(rys. 1) tłok gazowy

1 nie jest połączony z zespołem

suwadła

3; stanowi on oddzielną część, która przemiesz-

cza się ruchem prostoliniowym wewnątrz wkładki komory
gazowej

2. Impulsem wymuszającym ruch tłoka jest siła

od ciśnienia gazów prochowych rozprężających się w ko-
morze gazowej. Zespół suwadła składa się z suwadła
oraz zamka

5, który współpracuje z tuleją ryglową lufy 4.

Pod wpływem działania tłoka, zespół suwadła przemiesz-
cza się ruchem prostoliniowym w kierunku przeciwnym
do ruchu pocisku. Energia kinetyczna tłoka gazowego,
poprzez ruch suwadła, jest wykorzystywana do: odryg-
lowania zamka, wyrzucenia łuski z komory nabojowej,
napięcia sprężyny kurka oraz sprężyny mechanizmu po-
wrotnego

6, która wymusza ruch powrotny suwadła w kie-

runku obsady lufy. Zgromadzona w sprężynie mechaniz-
mu powrotnego energia umożliwia przesłanie kolejnego
naboju do komory nabojowej, zaryglowanie zamka w tulei
ryglowej lufy i przygotowanie broni do oddania kolejnego
strzału [1].

Analiza działania automatyki karabinka z wyko-

rzystaniem metod numerycznych.

Definiowanie mo-

delu

matematycznego

odwzorowującego

wzajemną

współpracę poszczególnych elementów automatyki bro-
ni jest zagadnieniem skomplikowanym, wymagającym
budowy układu równań algebraiczno-różniczkowych.
Podczas realizacji takich prac bardzo przydatne są
narzędzia, które wspomagają proces obliczeń inżynier-
skich. Umożliwiają one prowadzenie analiz inżynier-
skich, wykorzystując do tego celu zaawansowane meto-
dy numeryczne, z uwzględnieniem wielu istotnych czyn-
ników, które w klasycznym podejściu do modelowania
matematycznego często są pomijane. Przedstawiane
wyniki analiz numerycznych zostały zawężone do chara-
kterystyk przemieszczenia oraz prędkości określonych
dla podzespołu suwadła.

Analiza działania automatyki karabinka z wyko-

rzystaniem Metody Układów Wieloczłonowych.

W ce-

lu przeanalizowania zagadnienia wzajemnej współpracy
elementów automatyki broni należy przyjąć założenie, że
układ rzeczywisty jest układem wieloczłonowym (

multi-

body systems), reprezentowanym przez model złożony
z wielu członów sztywnych podlegających działaniu róż-
nego typu sił i powiązanych ze sobą połączeniami róż-
nych klas (parami kinematycznymi) [2]. Przyjęcie takiego
założenia pozwala na wykorzystanie aplikacji CAE – pro-
gramu MSC.visual Nastran w procesie rozwiązywania

dynamicznych równań ruchu wybra-
nych elementów automatyki kara-
binka, takich jak np. suwadło, czy
tłok gazowy, zgodnie z teorią New-
tona-Eulera

(II

prawo

Newtona

i twierdzenie dotyczące zmiany krę-
tu bryły sztywnej). Równania takie
są formułowane przy założeniu, że
układ własny

(związany z anali-

zowaną bryłą sztywną) jest układem
centralnym, umiejscowionym w śro-

dku masy

C. Podstawowe równania dynamiczne są wów-

czas w postaci wektorowej następujące [2, 3]:

(1)

MECHANIK NR 2/2011

121

Rys. 2. Model numeryczny analizowanego układu:

a) elementy skła-

dowe modelu numerycznego,

b) charakterystyka ciśnienia wymusza-

jącego ruch tłoka, c) charakterystyka sztywności modelu dyskretnego
sprężysto-tłumiącego

gdzie:

– składowe wektora prędkości (środka masy

C),

– siła wypadkowa,

– kręt ruchu obrotowego względem

środka masy

C,

– moment od sił zewnętrznych wzglę-

dem środka masy

C.

Składowe prędkości środka masy

C analizowanej bryły

zdefiniowane są w takim przypadku w osiach układu iner-
cyjnego

xyz i przyjmują postać

,

gdzie

v

c

jest prędkością uogólnioną. Składowe wektora

krętu

badanego ciała względem środka masy są

przedstawione w układzie osi

i zdefiniowane są

w sposób następujący:

gdzie

przy czym: J

c

– biegunowy moment bezwładności bryły

względem środka masy

C.

Równania ruchu analizowanego ciała sztywnego w takim

przypadku możemy zapisać w postaci macierzowej [2, 3]:

(2)

gdzie: I – 3

× 3 wymiarowa macierz jednostkowa, J

c

– bie-

gunowy moment bezwładności bryły względem środ-
ka masy

C, N

c

– moment od sił zewnętrznych (F ) wzglę-

dem środka masy

C danej bryły, ω – prędkość kątowa,

ω· – przyspieszenie kątowe, indeks górny (∼) oznacza
macierz skośnie symetryczną – operator mnożenia wek-
torowego.

Powyższe równanie można przedstawić w zapisie sym-

bolicznym [2, 3]:

(3)

gdzie M – jest

hxn – wymiarową, symetryczną macierzą

bezwładności, h(v) – wektor sił dynamicznych (macierz
kolumnowa), prawa strona równania, tj.

f jest zależna od

położenia i prędkości układu, a także od czasu

t.

Zależności kinematyczne w analizowanym przypadku

przyjmują postać:

(4)

gdzie: r·

c

= [

x

c

y

c

z

c

]

T

– wektor wodzący do środka masy

C

względem układu globalnego

xyz, I – jednostkowa

macierz 3

× 3, α – opisuje trzy kąty określające zmianę

położenia układu

względem układu

xyz, A(p)v – ma-

cierz transformacji pomiędzy składowymi prędkości v.

Przedstawiony model analityczny zaimplementowano

w oprogramowaniu typu CAE – MSC.visual Nastran.
Podejście to stanowi próbę rozwiązania problemu do-
tyczącego określenia dynamicznych charakterystyk dla
wybranych podzespołów składowych automatyki karabin-
ka metodami symulacyjnymi. Prace nad przygotowa-
niem modelu numerycznego rozpoczęto od wyekspor-
towania ze środowiska CAD, jakim jest program Solid
Works 2008, geometrii poszczególnych podzespołów
karabinka do uniwersalnego formatu wymiany danych
*.STEP.

Kolejny etap przygotowania analizy numerycznej zwią-

zany był z określeniem warunków początkowo-brzego-
wych. Obejmował on zdefiniowanie:

warunków brzegowych dla tłoka gazowego i suwadła

– określenie możliwości ruchu poprzez definicję stopni
swobody (rys. 2

a),

warunku wymuszenia oddziaływającego na tłok ga-

zowy (rys. 2

b) – charakterystyka ciśnienia,

par kontaktowych,

właściwości materiałowych dla poszczególnych części,

parametrów elementu o właściwościach sprężysto-

tłumiących (sprężyna mechanizmu powrotnego) – okreś-
lenie sztywności elementu (rys. 2

c).

Wymuszeniem uruchamiającym działanie analizowane-

go układu było ciśnienie na powierzchni czołowej tło-
ka gazowego (rys. 2

b). Przebieg funkcji ciśnienia zo-

stał określony doświadczalnie na stanowisku laboratoryj-
nym w trakcie strzelania, z jednoczesną rejestracją warto-
ści ciśnienia w komorze gazowej. Sprężynę mechanizmu
powrotnego zdefiniowano za pomocą elementu o właś-
ciwościach sprężysto-tłumiących, a dane niezbędne do
określenia jej sztywności uzyskano z dokumentacji kon-
strukcyjnej (rys. 2

c).

Sformułowanie warunków początkowo-brzegowych dla

poszczególnych części automatyki karabinka wiązało się
z określeniem ich stopni swobody. Jako przykład przed-
stawiono sposób definiowania warunków dla podzespołu
tłoka gazowego oraz suwadła. Dla analizowanego ukła-
du, tłok gazowy ma dwa stopnie swobody: możliwość
przemieszczania się oraz obrotu wzdłuż osi w zakresie
ograniczonym wymiarami wkładki komory gazowej. Su-
wadło ma jeden stopień swobody – możliwość ruchu
posuwisto-zwrotnego wzdłuż osi przewodu lufy. Ograni-
czenia ruchu suwadła zostały wprowadzone do układu
poprzez zdefiniowanie par kontaktowych bryły suwadła
z takimi elementami, jak: prowadnice suwadła, obsada
lufy, tylec mechanizmu powrotnego, podzespół zamka
oraz wodzik zamka. Tłok gazowy został zdefiniowany
jako element współpracujący z: suwadłem, wkładką ko-
mory gazowej oraz regulatorem gazowym. Wszystkie
elementy w analizowanym układzie wiernie odwzorowały
charakterystyki masowe i geometryczne rzeczywistego
obiektu. Ze względu na typ prowadzonej analizy, wszyst-
kie ciała były bryłami sztywnymi (nieodkształcalnymi).
Przyjęte do analizy wstępne warunki początkowo-brze=
gowe nie uwzględniają wielu istotnych czynników, w tym
np. dyssypacji energii w wyniku procesu tarcia oraz
zmian zachodzących w układzie na skutek oddziaływań
termicznych w elementach węzła gazowego. Następ-
ny etap realizacji prac związanych z uruchomieniem
analizy numerycznej obejmował definiowanie paramet-
rów symulacji, takich jak: określenie kroku całkowania
i warunków związanych z przyjętą tolerancją; wybór
metody całkowania Kutta-Mersona [4]. Na podsta-
wie przeprowadzonej analizy numerycznej otrzymano
rozwiązanie w postaci charakterystyk dynamicznych
oraz

kinematycznych

poszczególnych

podzespołów

składowych automatyki karabinka. Jako przykład roz-
wiązania przedstawiono wykresy krzywych przemiesz-
czenia oraz prędkości określone dla podzespołu su-
wadła (rys. 3).

122

MECHANIK NR 2/2011

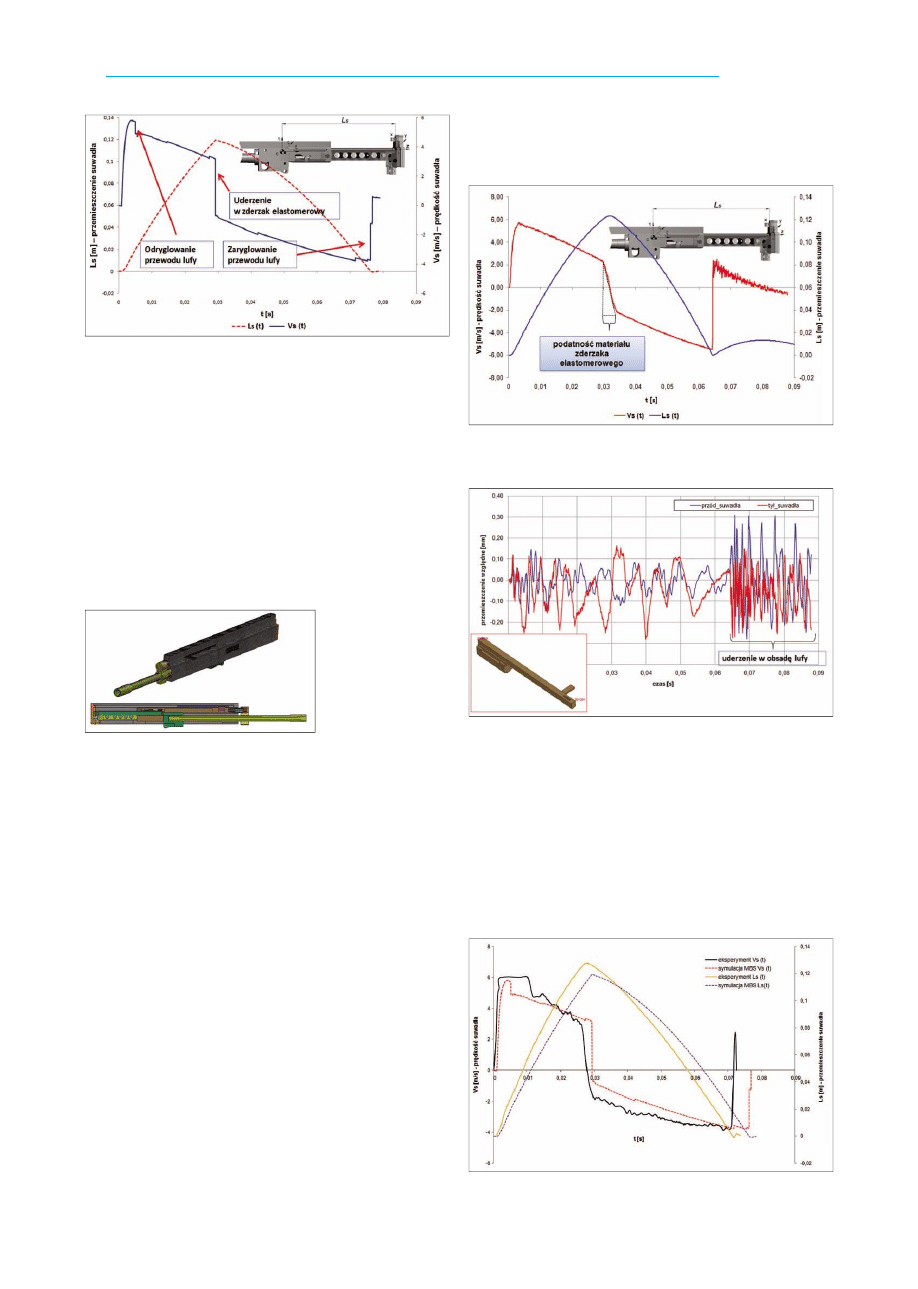
Rys. 3. Wykres przemieszczenia oraz prędkości podzespołu suwadła
wzdłuż osi

Z

Rys. 4. Widok ogólny
analizowanego

mo-

delu

numerycznego

MES

Rys. 5. Wykres przemieszczenia oraz prędkości podzespołu suwadła
względem osi przewodu lufy

Rys. 6. Wykres przemieszczeń względnych podzespołu suwadła
w płaszczyźnie poziomej

Rys. 7. Porównanie wyników analizy numerycznej Metodą Układów
Wieloczłonowych z wynikami strzelania

Określenie charakterystyk dynamicznych pod-

zespołu suwadła z wykorzystaniem Metody Ele-
mentów Skończonych.

Drugi wariant badań numerycz-

nych układu automatyki karabinka zrealizowano za po-
mocą Metody Elementów Skończonych w środowisku
programu LS-Dyna. Prace nad przygotowaniem symu-
lacji komputerowej rozpoczęto od budowy modelu nu-
merycznego w programie HyperMesh, gdzie uproszczo-
ny model geometryczny poszczególnych części funk-
cjonalnych automatyki karabinka podzielono na ok.
100 tys. elementów skończonych typu heksagonalnego
(rys. 4).

Kolejny etap prac przygotowawczych związany był

z definiowaniem warunków początkowo-brzegowych. Wy-
muszeniem uruchamiającym działanie automatyki kara-
binka była siła od ciśnienia gazów prochowych, działają-
ca na elementy węzła gazowego, takie jak: powierzchnia
czołowa tłoka gazowego, ścianki wewnętrzne komory
gazowej oraz wkładki komory gazowej. W analizowanym
przypadku

zdefiniowano

dodatkową

charakterystykę

ciśnienia, zmienną w funkcji czasu, działającą wewnątrz
przewodu lufy. Poprzez określenie 34 par kontaktowych
zdefiniowano stopnie swobody poszczególnych części
składowych układu automatyki broni.

Podobnie jak

w przypadku Metody Układów Wieloczłonowych, spręży-
nę mechanizmu powrotnego zdefiniowano za pomocą
elementu o właściwościach sprężysto-tłumiących. Prze-
prowadzenie analizy numerycznej z wykorzystaniem Me-
tody Elementów Skończonych umożliwiło uwzględnienie
dyssypacji energii kinetycznej części ruchomych w wyni-
ku procesu tarcia oraz podatności materiału zderzaka
elastomerowego poprzez opisanie jego właściwości mo-
delem konstytutywnym Mooneya-Rivlina [5]. Zasadni-
czą wadą wybranej metody obliczeniowej jest długi czas
trwania obliczeń, który dla rozpatrywanego przypadku
wyniósł 3 dni (zadanie wykonano na ośmiu procesorach).
Na podstawie przeprowadzonej symulacji komputerowej
otrzymano rozwiązanie równań opisujących dynamiczny
charakter współpracy poszczególnych elementów skła-
dowych automatyki karabinka. Jako przykładowe wyniki

przedstawiono przebiegi krzywych przemieszczenia oraz
prędkości określonych dla podzespołu suwadła (rys. 5,
6).

Porównanie wyników badań numerycznych
uzyskanych ze strzelania

Otrzymane w drodze symulacji komputerowych wyniki

pozwoliły na szybką analizę zaproponowanego rozwiąza-
nia konstrukcyjnego. Aby uwiarygodnić ich jakość, prze-
prowadzono dodatkowe badania doświadczalne, których
wyniki porównano z numerycznymi (rys. 7, 8). Ekspery-
menty realizowano poprzez strzelanie i jednoczesny po-

MECHANIK NR 2/2011

123

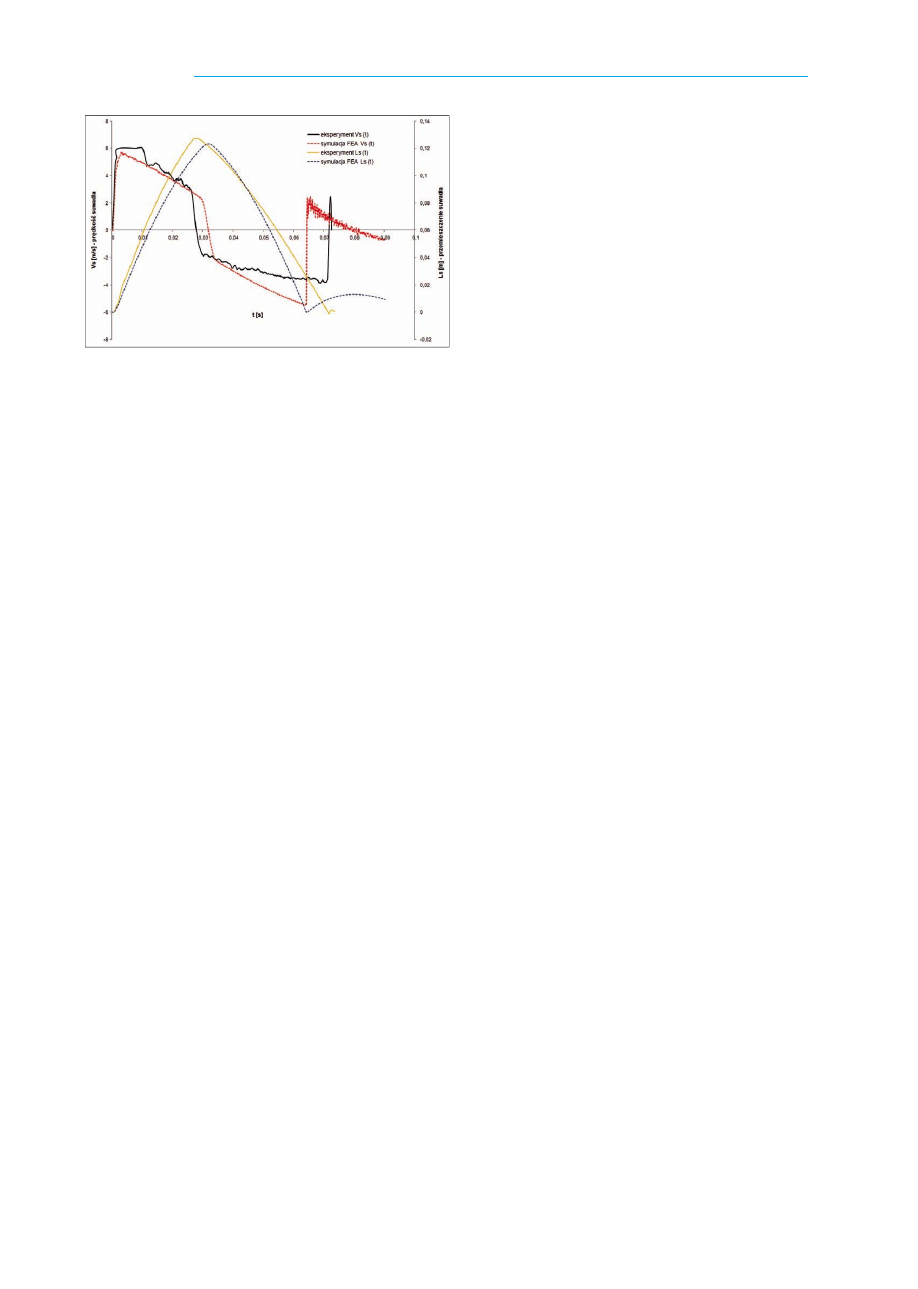
Rys. 8. Porównanie wyników analizy numerycznej Metodą Elemen-
tów Skończonych z wynikami doświadczalnymi

miar przemieszczenia suwadła, za pomocą kamery do
rejestracji przebiegów szybkozmiennych. Na podstawie
otrzymanego wykresu przemieszczenia w funkcji czasu
możliwe było wyznaczenie krzywej prędkości.

Wykorzystanie programów CAE w procesie projekto-

wania broni strzeleckiej pozwala na szybką ocenę za-
proponowanych rozwiązań konstrukcyjnych. Opracowane
modele numeryczne umożliwiają prowadzenie badań
symulacyjnych bez konieczności wykonywania kosztow-
nych i długotrwałych badań. Zdefiniowane warunki po-

czątkowo-brzegowe, takie jak: sztywność sprężyny me-
chanizmu powrotnego, wartość impulsu wymuszenia,
właściwości materiałowe, opisujące poszczególne ele-
menty, mogą być dowolnie konfigurowane. Analiza kom-
puterowa z wykorzystaniem zbudowanych modeli nume-
rycznych pozwala na określenie odpowiedzi układu, w za-
leżności od przyjętych warunków początkowo-brzego-
wych. Porównanie wyników uzyskanych z badań numery-
cznych i eksperymentu wskazuje na ich stosunkowo dużą
zgodność. Pozwalają na wstępne wyznaczenie istotnych
charakterystyk pozostałych elementów układu, np. tłoka
gazowego i zamka. Dzięki temu możliwe jest ogranicze-
nie zakresu badań doświadczalnych.

LITERATURA

1. J. GACEK, J. MAŁACHOWSKI, P. PŁATEK, R. WOŹNIAK: Wstę-

pna analiza procesu dynamicznego oddziaływania tłoka gazo-
wego z suwadłem dla modułowego systemu broni strzeleckiej
MSBS kal. 5,56 mm. XIV Szkoła Komputerowego Wspomaga-
nia Projektowania, Wytwarzania i Eksploatacji, Jurata 10

÷ 14.05.

2010.

2. J. FRĄCZEK, M. WOJTYRA: Kinematyka układów wieloczłono-

wych. Metody obliczeniowe. WNT Warszawa 2007.

3. W. BLAJER: Metody dynamiki układów wieloczłonowych. Poli-

technika Radomska 1998.

4. MSC.visual Nastran 4D. Quick Reference Guide, 2001.
5. T. BELYTSCHKO, W. K. LIU, B. MORAN: Nonlinear Finite Ele-

ments for continua and structures. John Wiley & Sons England
2000.

Praca naukowa finansowana ze środków na naukę w latach

2007-2010 jako projekt rozwojowy.