A new method to develop typical weather years in different climates for building
energy use studies

Liu Yang

a

, Kevin K.W. Wan

b

, Danny H.W. Li

b

, Joseph C. Lam

b

,

*

a

School of Architecture, Xi

’an University of Architecture and Technology, Shaanxi 710055, China

b

Building Energy Research Group, Department of Civil and Architectural Engineering, City University of Hong Kong, Tat Chee Avenue, Kowloon, Hong Kong SAR, China

a r t i c l e i n f o

Article history:
Received 12 April 2011
Received in revised form
25 July 2011
Accepted 29 July 2011
Available online 1 September 2011

Keywords:
Principal component analysis
Typical weather years
Building energy use
Climate change
General circulation models
China

a b s t r a c t

Principal component analysis of 30-year long-term meteorological variables was conducted. Typical
principal component years (TPCYs) were determined for Harbin, Beijing, Shanghai, Kunming and Hong
Kong representing the

five major architectural climates across China: severe cold, cold, hot summer and

cold winter, mild, and hot summer and warm winter. In each climate zone, the TPCY was compared with
the 30 individual years and the widely used typical meteorological year (TMY). The monthly principal
component and the predicted total building energy consumption based on the TPCY and TMY were very
close to the 30-year long-term mean estimation. TPCY for the 21st century in each of the

five cities was

also identi

fied using predictions from general climate models. The TPCY approach is a good alternative to

the TMY method. Firstly, predicted building energy use from TPCY is closer to the long-term estimation
than that from the TMY in different climates. Secondly, because only monthly data are considered, the
development of TPCY is much simpler and less time-consuming. This would have important applications
in the regular updating of typical weather years for building energy studies and in the assessment of the
impact of climate change on energy use in the built environment.

Ó 2011 Elsevier Ltd. All rights reserved.

1. Introduction

Recent reports by the Inter-governmental Panel on Climate Change

(IPCC) had raised public awareness of energy use and the environ-
mental implications

[1,2]

. Carbon emissions from the use of energy in

buildings were one of the major components in the overall emissions
scenarios. It was estimated that in 2002, buildings accounted for 33% of
the global greenhouse gas emissions

[3]

. There has been a steady

increase in energy use in China since the adoption of the Policy of
Reforming and Opening in the 1980s. Building stocks accounted for
about 24.1% of total national energy use in 1996, rising to about 27.5%
in 2001, and was projected to increase to about 35% in 2020

[4,5]

.

Although carbon emissions per capita in China are low, its total
emissions in 2005 accounted for 19% of the global emissions and were
only second to the US

[6]

. In 2007, with 6.1 Gt (10

9

tonnes) of energy-

related CO

2

emissions China overtook the US

[7]

. In 2009, the total

energy consumption reached 3.1 billion tons of standard coal equiv-
alent, accounting for about 14.3% of the world total

[8]

. When the life-

cycle energy use and emissions footprint are considered, buildings
account for a signi

ficant proportion of the energy-related emissions.

One way to alleviate the ever-growing demand for energy is to have
more energy-ef

ficient building designs and proper building energy

conservation programmes

[9]

.

Building designs and energy use in the built environment are

directly related to the prevailing climates. Studies on the long-term
climatic variations in China had found changes in the local climates
and the heat/cold stresses in the different climate zones especially
during the last two decades of the 20th century

[10

e12]

. Buildings

typically have a long life span, lasting for 50 years or more. It is,
therefore, important to be able to investigate how buildings will
respond to climate change in the future and assess the likely changes in
energy use. Building energy simulation is an acceptable technique for
assessing the dynamic interactions between the external climates, the
building envelope and the heating, ventilation and air-conditioning
(HVAC) system and the corresponding energy consumption. It has
played an important role in the development of simple design tools
and building energy ef

ficiency codes

[13

e15]

. A key element in

building energy simulation is the 8760 hourly records of weather data,
representative of the prevailing weather conditions. All energy simu-
lation computer programs require weather data input to drive the
thermal models within the simulation tools.

The purpose and end-use of the building energy simulation

must be considered when choosing the weather data. Broadly
speaking, there are three types of hourly weather data for building

* Corresponding author. Tel.: þ86 852 3442 7606; fax: þ86 852 3442 0427.

E-mail address:

[e-mail]

(J.C. Lam).

Contents lists available at

ScienceDirect

Energy

j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / e n e r g y

0360-5442/$

e see front matter Ó 2011 Elsevier Ltd. All rights reserved.

doi:

10.1016/j.energy.2011.07.053

Energy 36 (2011) 6121

e6129

energy simulation, namely multi-year data sets, typical weather
years and representative days. Adopting a multi-year data set is
sometimes not feasible and economical for the common building
design and analysis, whereas representative days are often too
limited and not detailed enough for a speci

fic design and analysis

problem. Therefore, for detailed building energy analysis, typical
years are the most commonly used. The typical weather year
approach can reduce the computational efforts in simulation and
weather data handling by using one year instead of multiple years.
Besides, a consistent form of weather data is ensured so that results
from different studies can be compared. The development of
a typical weather year from a multi-year database, however, can be
time-consuming or even not practicable. For instance, the devel-
opment of a typical meteorological year (TMY) in climate change
studies for the 21st century for a particular location would involve
downloading 100 years of hourly/daily predictions from general
circulation models (GCMs). There would also be an enormous
amount of statistical analysis of the long-term frequency distribu-
tions of the different meteorological variables such as temperature,
humidity and solar radiation. Though not insurmountable, a simple
approach using only monthly data to select the 12 typical months to
form a typical weather year would certainly be more desirable.
Earlier work on long-term trends of energy consumption in
buildings involving principal component analysis of key monthly
meteorological variables indicated good correlation between the
long-term weather conditions and the corresponding sector-wide
energy consumption

[16]

as well as building energy simulation

results

[17,18]

. The objective of the present work was, therefore, to

investigate the feasibility of using principal component analysis
technique to develop an alternative approach to select a typical
weather year within each of the major climate zones across China
and assess its suitability for building energy estimation.

2. Methodology

First of all, major climates relevant to building energy studies

were identi

fied from existing climate classifications. A city within

each climate zone was then selected for this study. For each city the
12 typical meteorological months (TMMs) were determined and
the corresponding TMY was developed accordingly. Likewise,
principal component analysis of major meteorological variables
was conducted so that the 12 typical principal component months
(TPCMs) could be developed to form the typical principal compo-
nent year (TPCY). Multi-year building energy simulation was then
conducted using the hourly weather data from each of the 30 years,
the TMY and the TPCY. The suitability of the TPCY for building
energy studies was assessed in terms of its ability to produce
predictions close to the 30-year long-term mean energy estimation
through statistical analysis. Attempts were also made to develop
the 12 TPCMs in the 21st century in each of the major climate zones
identi

fied using predictions from general circulation models.

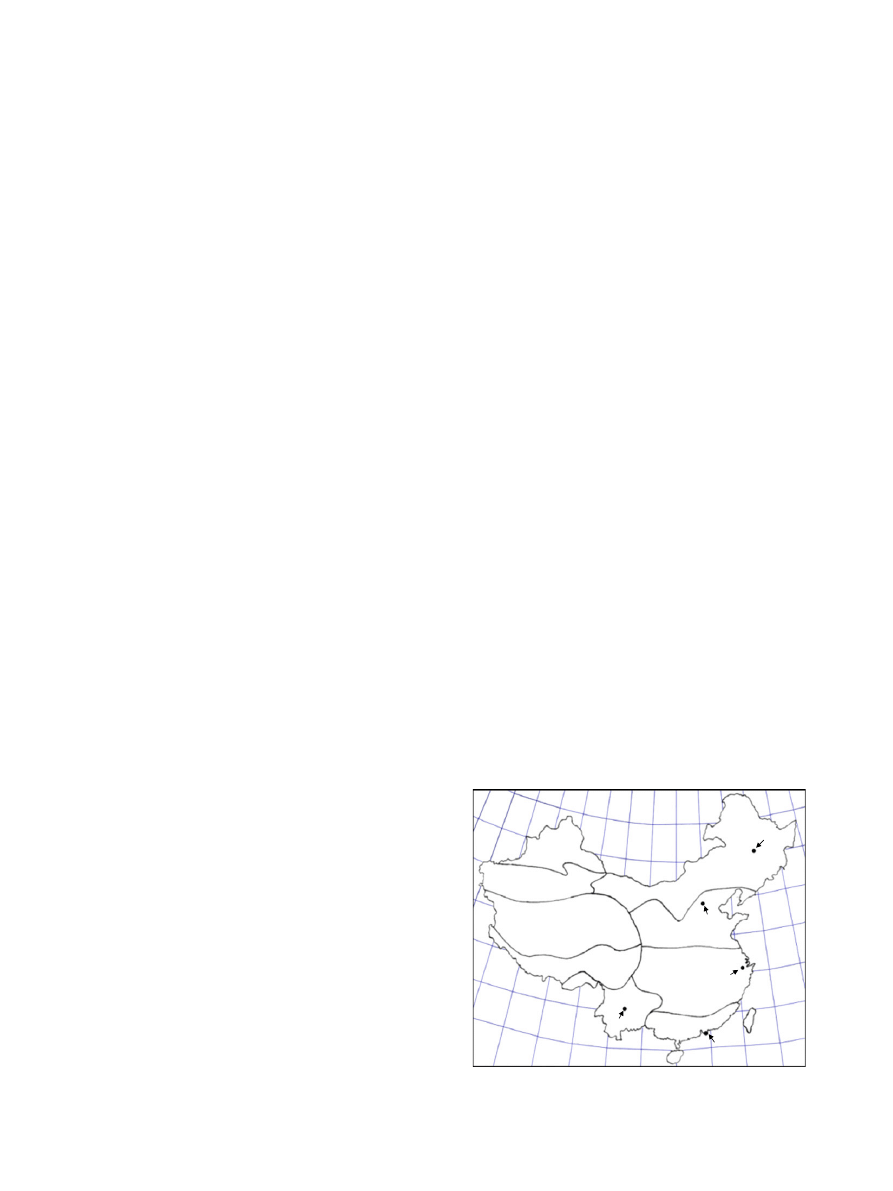
3. Major climate zones and cities

China is a large country with an area of about 9.6 million square

kilometres. Approximately 98% of the land area stretches between
a latitude of 20

N and 50

N, from the subtropical zones in the south

to the temperate zones (including warm-temperate and cool-
temperate) in the north

[19]

. The maximum solar altitudes vary

a great deal and there is a large diversity of climates, especially the
temperature distributions during winter. Characteristics associated
with continental climates can be identi

fied, with warmer summers,

cooler winters and a larger annual temperature range than other
parts of the world at similar latitudes. China also has a complex
topography ranging from mountainous regions to

flat plains. This

diversity and complexity have led to many different regions with
distinct climatic features

[20]

. There are various ways to classify

climate types or zones according to different criteria using different
climatic variables and indices. In China, the most commonly used
one is for the thermal design of buildings, concerning mainly
conduction heat gain/loss and the corresponding thermal insulation
issues. It has

five climate types: severe cold, cold, hot summer and

cold winter, mild, and hot summer and warm winter

[21]

. The

zoning criteria are mainly based on the average temperatures in the
coldest and hottest months of the year. The number of days that
daily average temperature is below 5

C or above 25

C is counted as

the complementary indices for determining the zones.

Fig. 1

shows

an overall layout of the

five major architectural climates. Because of

the varying topology and elevations, there are nine regions

e both

the severe cold and cold climates have three regions. A city was
selected within each of the

five major climate zones: Harbin (severe

cold, 45

45

0

N/126

46

’E), Beijing (cold, 39

48

’N/116

28

’E), Shanghai

(hot summer and cold winter, 31

10

’N/121

26

’E), Kunming (Mild,

25

01

’N/102

41

’E) and Hong Kong (hot summer and warm winter,

22

18

’N/114

10

’E).

4. Development of typical meteorological years (TMYs)

A TMY was developed for each of the

five cities within the major

climate zones. Details of the TMY concept and development work
can be found in Lam et al.

[22]

, Ecevit et al.

[23]

and Yang et al.

[24]

.

Brie

fly, the TMY method developed by the Sandia National Labo-

ratories in the United States is one of the most widely adopted for
determining typical weather years

[25]

. A TMY consists of 12

typical meteorological months (TMMs) selected from various
calendar months in a multi-year weather database. For example,
the January of 1980 may be selected as the

first TMM, the February

of 1989 as the second TMM, and so on. The 12 months selected will
then be combined to form the TMY. Smoothing of data for
discontinuities is usually required to avoid abrupt changes at the
boundary between two adjacent months selected from different
years. Selection of a TMM is based on the statistical analysis and
evaluation of four climatic variables: dry-bulb temperature (DBT),
dew-point temperature (DPT), wind speed (WSP) and global solar
radiation (GSR). In general, nine indices are considered including
the daily maxima, minima and means of DBT and DPT, the daily
maximum and mean values of WSP and the daily total GSR.

Hot summer &
cold winter

70

75

80

85

90

95

100

105

110

115

120

125

130

135

50

45

40

35

30

25

20

45

40

35

30

25

20

85

90

95

100

105

110

115

120

125

Severe cold

Cold

Severe cold

Cold

Cold

Beijing

Severe cold

Hot summer &
warm winter

Mild

Shanghai

Harbin

Hong Kong

Kunming

Fig. 1. Major architectural climates across China and geographical distribution of the
five cities.

L. Yang et al. / Energy 36 (2011) 6121

e6129

6122

A summary of the nine daily indices and their respective weightings
is shown in

Table 1

. It can be seen that version 2 of TMY (i.e. TMY2)

also includes direct radiation in the selection of TMM

[26]

.

The TMM selection involves minimising the difference between

the cumulative distribution function (CDF) of the month being
considered and the long-term CDF using a nonparametric method
known as Finkelstein-Schafer (FS) statistics

[27]

. An empirical CDF,

which is a monotonic increasing function, is de

fined as follows:

S

n

x

¼

8

<
:

0

for x

< x

ð1Þ

ðk 0:5Þ=n for x

ðkÞ

x x

ðkþ1Þ

1

for x

x

ðnÞ

(1)

where

S

n

(x)

¼ value of the cumulative distribution function at x

n

¼ total number of elements

k

¼ rank order number ¼ 1, .., n 1

Values of the FS statistics are calculated for each of the daily

indices (see

Table 1

) using the following equation:

FS

¼

1

N

X

N

i

¼ 1

d

i

(2)

where

FS

¼ value of FS test statistics

d

i

¼ absolute difference between the long-term CDF and the

yearly CDF at x(i) value
N

¼ the number of daily readings for that month (e.g. for

January, N

¼ 31)

The procedure assumes that a TMY consisting of the 12 TMMs

would have weather patterns and system performance characteristics

close to the long-term climatic conditions. It is generally believed that
the longer the period of record used, the more representative of the
prevailing long-term climate patterns of a particular location the
results would be. Selection of a comparatively short historical period
of record would not re

flect the long-term climatic conditions. For

building energy calculations, it was found that a 30-year record would
produce conservatively stable temperature patterns

[28]

. Weather

data measured during the 30-year period (1971

e2000 for the four

mainland cities and 1979

e2008 for Hong Kong) were gathered and

analysed. The basic process on frequency distributions was performed
to determine the values of the nonparametric statistics for each of the
seven indices shown in

Table 1

. The year closest to the long-term mean

distribution (i.e. with the lowest weighted-sum average of the FS test
statistics) was selected as the TMM.

Table 2

shows a summary of the

12 TMMs selected for each of the

five cities.

5. Development of typical principal component years (TPCYs)

In the analysis of long-term meteorological variables, it is often

advantageous to group key weather variables directly affecting
building energy performance. Principal component analysis (PCA)
is a multivariate statistical technique for analysis of the depen-
dencies existing among a set of inter-correlated variables

[29,30]

.

Due to its ability to categorise the complex and highly inter-
correlated set of meteorological variables as one or more cohesive
indices, PCA tends to give a better understanding of the cause/effect
relationship. PCA is conducted on centred data or anomalies, and is
used to identify patterns of simultaneous variations. Its purpose is
to reduce a data set containing a large number of inter-correlated
variables to a data set containing fewer hypothetical and uncorre-
lated components, which nevertheless represents a large fraction of
the variability contained in the original data. These components are
simply linear combinations of the original variables with coef

fi-

cients given by the eigenvector.

Initially,

five climatic variables were considered: dry-bulb

temperature (DBT, in

C), wet-bulb temperature (WBT, in

C),

global solar radiation (GSR, in MJ/m

2

), clearness index and wind

speed. DBT affects the thermal response of a building and the
amount of heat gain/loss through the building envelope and energy
use for the corresponding sensible cooling/heating requirements.
WBT dictates the amount of humidi

fication required during the dry

winter days and the latent cooling under humid summer condi-
tions. Information on solar radiation is crucial to cooling load
determination and the corresponding design and analysis of air-
conditioning systems. In the tropical and subtropical climates, solar
heat gain through the fenestrations is often the largest component
of the building envelope cooling load

[31,32]

. For colder climates,

solar heat could be a key design factor in both passive and active

Table 1
Weighting factors for the Finkelstein-Schafer statistics.

Index

Sandia method
TMY

[24]

NSRDB
TMY2

[25]

Present
study

Temperature

Max dry-bulb temp

1/24

1/20

1/24

Min dry-bulb temp

1/24

1/20

1/24

Mean dry-bulb temp

2/24

2/20

2/24

Humidity

Max dew-point temp

1/24

1/20

e

Min dew-point temp

1/24

1/20

e

Mean dew-point temp

2/24

2/20

4/24

Wind

Max wind speed

2/24

1/20

2/24

Mean wind speed

2/24

1/20

2/24

Solar

radiation

Global radiation

12/24

5/20

12/24

Direct radiation

e

5/20

e

Table 2
Summary of the 12 typical meteorological months (TMMs) and typical principal component months (TPCMs) selected for the

five cities.

Harbin

Beijing

Shanghai

Kunming

Hong Kong

TMM

TPCM

TMM

TPCM

TMM

TPCM

TMM

TPCM

TMM

TPCM

Jan

1982

1974

1988

1974

1982

1978

1989

1990

1995

2006

Feb

1982

1975

1981

1996

1981

1994

1989

1991

1988

1998

Mar

1982

1978

1983

1996

1979

1979

1971

1978

2003

2006

Apr

1984

1991

1985

1995

1990

1993

1986

1987

1980

1987

May

1986

1971

1984

1992

1976

1980

1993

1973

1997

2005

Jun

1986

1972

1984

1974

1973

1972

1984

1998

1990

1990

Jul

1990

1977

1991

1977

1986

1983

1989

1979

2000

1985

Aug

1980

1999

1983

1990

1986

1991

1977

1972

2003

1982

Sep

1981

1989

1984

1976

1982

1984

1990

1971

1982

1982

Oct

1987

1989

1984

1994

1980

1975

1992

1985

1984

1984

Nov

1982

1993

1984

1984

1989

1996

1982

1985

1989

1990

Dec

1983

1983

1994

1972

1972

1995

1993

1976

2001

2001

L. Yang et al. / Energy 36 (2011) 6121

e6129

6123

solar designs for buildings with substantial space heating require-
ments

[15]

. Clearness index indicates the prevailing sky conditions

while wind speed affects natural ventilation and the external
surface resistance and hence the U-values of the building envelope.
Contributions to the principal components from the clearness
index and wind speed, however, were found to be small compared
with the DBT, WBT and GSR [

17,33

]. These 2 climatic variables were,

therefore, not considered.

The 30-year monthly data for the three meteorological variables

were gathered and analysed. Altogether 30

12 3 data were

considered in the PCA for each city.

Table 3

shows the coef

ficients of

the three principal components and the relevant statistics from the
PCA for Harbin. The eigenvalue is a measure of the variance
accounted for by the corresponding principal component. The

first

and largest eigenvalue accounts for most of the variance, the
second accounts for the second largest amounts of variance, and so
on. A common approach is to select only those with eigenvalues
equal to or greater than one (eigenvalues greater than one imply
that the new principal components contain at least as much
information as any one of the original climatic variables

[34]

) or

with at least 80% cumulative explained variance

[35]

. These criteria

were adopted for this study. From

Table 3

, it can be seen that the

first principal component had an eigenvalue greater than one with
a cumulative explained variance exceeding 90% (i.e. a one-
component solution would account for more than 90% of the
variance in the original climatic variables). Similar features were
observed for the other four cities. The

first principal component

was, therefore, retained and a new set of monthly variable, Z,
determined as a linear combination of the original three climatic
variables as follows:

Z

¼ A DBT þ B WBT þ C GSR

(3)

Table 4

shows a summary of the coef

ficients A, B and C for the five

cities. Measured data for the three climatic variables were analysed
and the monthly values of Z determined for the 30-year period. As
mentioned earlier, there was a close correlation between energy use
in buildings and the principal component Z. It was, therefore, argued
that for a particular calendar month, the year with a monthly Z closest
to the 30-year long-term average would possess weather character-
istics similar to the long-term situation. The year with the Z closest to
the long-term average was thus selected as the typical principal
component month (TPCM).

Table 2

shows a summary of the 12

TPCMs determined for the

five cities. It can be seen that the number of

months that have the same year selected for both the TMM and TPCM
was small, ranging from none in Kunming (mild climates) to four in
Hong Kong (hot summer and warm winter). To have a better
understanding of the differences, pro

files of the monthly Z for the

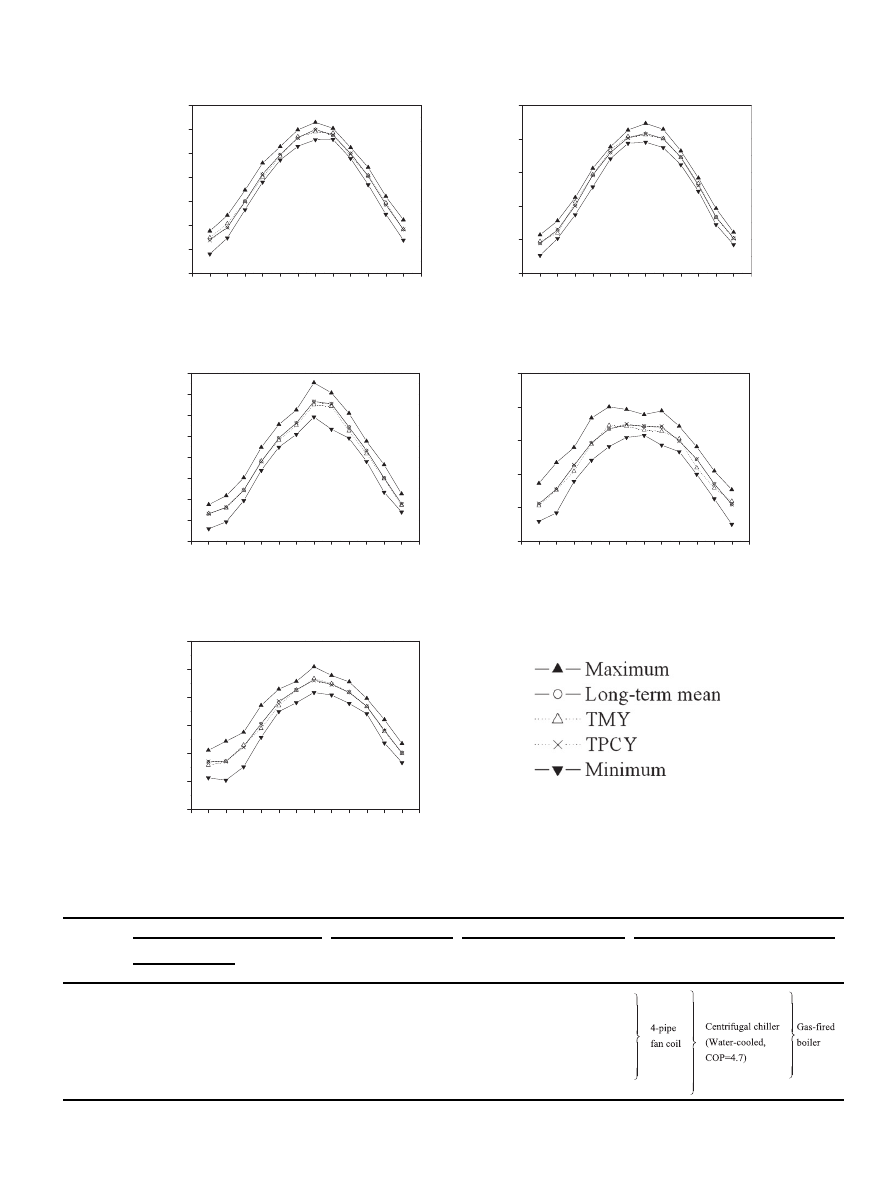
TMY and TPCY were compared with those from the 30 individual
years. For each city,

five profiles were considered e the range of

maximum and minimum monthly Z from the 30 individual years,
long-term mean (i.e. the 30-year average), TMY and TPCY. A summary
is shown in

Fig. 2

. In general, TMY and TPCY fell within the minimum

and maximum ranges and tended to follow the long-term means
quite closely. It is interesting to see that although the years selected

for the TMMs and TPCMs were mostly different, the monthly Z for all
the 12 calendar months were rather close to each other in all

five

cities. In Harbin, the annual principal component Z for the long-term
mean, TMY and TPCY was 17.45, 17.59 and 17.39, respectively; Beijing
32.83, 32.14 and 32.77; Shanghai 39.54, 38.74 and 39.47; Kunming
34.74, 34.15, and 34.79; and Hong Kong 52.15, 51.86 and 52.09. This
suggests that although the selection methods and the actual typical
months selected were different, TMY and TPCY exhibited similar
weather characteristics at least in terms of the principal component Z
and followed the long-term mean quite closely.

6. Comparisons of building energy use estimations from
different weather years

Apart from ensuring that key climatic variables of the TMY and

TPCY closely follow their long-term values and statistically represent
the prevailing weather conditions, it is also important to ascertain
whether these typical weather years do produce simulation results
that are close to the long-term means. Hour-by-hour energy simu-
lations were conducted for each of the 30 years using the simulation
tool VisualDOE4.1

[36]

. Two major inputs were considered for the

simulation: (i) 8760 hourly records of weather data (DBT, WBT, GSR,
wind speed and wind direction), and (ii) a generic of

fice building for

each city, details of which can be found in Wan et al.

[15]

. Brie

fly, it

was a 35 m

35 m, 40-storey building with curtain walling design,

3.4 m

floor-to-floor height and 40% window-to-wall ratio. The total

gross

floor area (GFA) was 49000 m

2

(41160 m

2

air-conditioned and

7840 m

2

non-air-conditioned). The air-conditioned space had

five

zones - four at the perimeter and one interior. Obviously, each city
would in reality have rather different building envelope designs to
suit the local climates. Generic building envelopes and HVAC designs
were developed based on the prevailing architectural and engi-
neering practices and the local design/energy codes in the four cities
on the mainland

[37,38]

and in Hong Kong

[39,40]

.

Table 5

shows

a summary of the key design parameters.

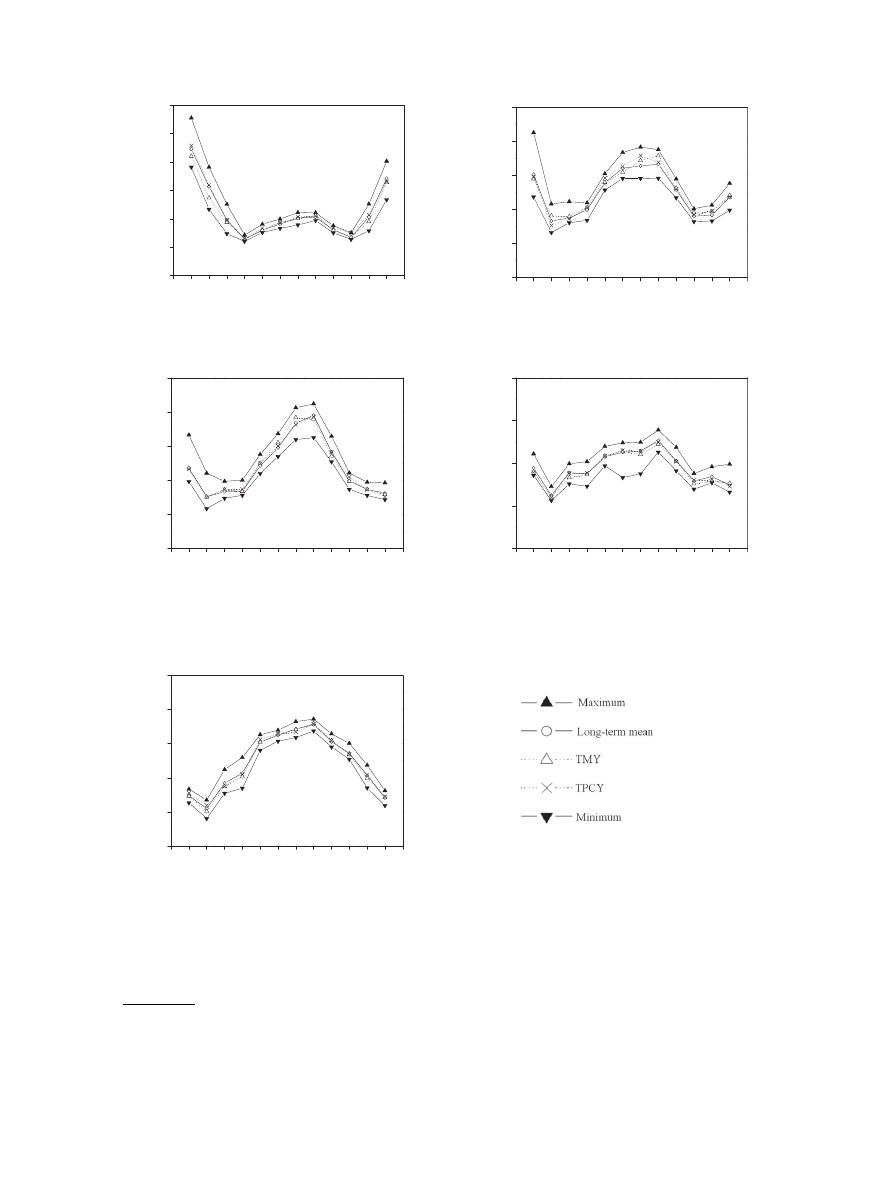
For each city, the total building energy consumption predicted

from the 32 simulation runs (i.e. 30 individual years plus TMY and
TPCY) were analysed. Monthly energy use from the TMY and TPCY
was compared with those from the 30 individual years, and
a summary for the

five cities is shown in

Fig. 3

. Again, it can be seen

that both the TMY and TPCY predictions were within the maximum
and minimum ranges and tended to follow the long-term means
rather closely. To get an idea about variations of the predicted
monthly energy consumption from different years, mean bias error
(MBE) and root mean square error (RMSE) were determined for
each of the 32 simulated results as follows:

MBE

j

¼

X

12

i

¼ 1

ðx

i

y

i

Þ

12

(4)

where

x

ij

¼ monthly total building energy use for each year (j ¼ 1e32)

y

i

¼ monthly total building energy use for the 30-year long-term

mean

Table 3
Summary of principal component analysis of dry-bulb temperature (DBT), wet-bulb
temperature (WBT) and global solar radiation (GSR) for Harbin.

Principal
component

Eigenvalue

Cumulative explained
variance (%)

Coef

ficient

DBT

WBT

GSR

1st

2.898

96.58

0.992

0.990

0.966

2nd

0.100

99.91

0.121

0.133

0.260

3rd

0.003

100

0.038

0.037

0.001

Table 4
Summary of the coef

ficients for the principal component.

City

A

B

C

Harbin

0.992

0.990

0.966

Beijing

0.983

0.967

0.883

Shanghai

0.980

0.974

0.883

Kunming

0.997

0.967

0.304

Hong Kong

0.977

0.940

0.628

L. Yang et al. / Energy 36 (2011) 6121

e6129

6124

J

F

M

A

M

J

J

A

S

O

N

D

-60

-40

-20

0

20

40

60

80

Monthly

principa

l co

mpon

ent Z

Month

Harbin

J

F

M

A

M

J

J

A

S

O

N

D

-20

0

20

40

60

80

Monthly

principa

l co

mpon

ent Z

Month

Beijing

J

F

M

A

M

J

J

A

S

O

N

D

0

10

20

30

40

50

60

70

80

Monthly principa

l

co

mpon

ent

Z

Month

Shanghai

J

F

M

A

M

J

J

A

S

O

N

D

10

20

30

40

50

60

Monthly principa

l

co

mpon

ent

Z

Month

Kunming

J

F

M

A

M

J

J

A

S

O

N

D

20

30

40

50

60

70

80

M

onthly pr

inc

ip

al com

p

onen

t Z

Month

Hong Kong

Fig. 2. Comparison of monthly Z between TMY, TPCY and 30-year long-term mean for the

five cities.

Table 5
Summary of the key building envelope and HVAC design data for the

five cities (Ref.

[14]

).

City

Building envelope

Indoor design condition

Internal load density

HVAC

U-value (W/m

2

K)

Window shading
coef

ficient

Summer (

C)

Winter (

C)

Occupancy
(m

2

/person)

Lighting
(W/m

2

)

Equipment
(W/m

2

)

AHU

Cooling

Heating

Wall

Window

Roof

Harbin

0.44

2.50

0.35

0.64

25

20

8

18

13

Beijing

0.60

2.60

0.55

0.70

25

20

8

18

13

Shanghai

1.00

3.00

0.70

0.55

25

20

8

18

13

Kunming

1.47

3.50

0.89

0.50

25

20

8

18

13

Hong Kong

2.01

5.60

0.54

0.40

24

21

13

15

10

VAV

Electric

Notes: HVAC

¼ Heating, ventilation and air-conditioning; AHU ¼ Air-handling unit; VAV ¼ Variable-air volume.

L. Yang et al. / Energy 36 (2011) 6121

e6129

6125

RMSE

j

¼

ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

X

12

i

¼ 1

ðx

i

y

i

Þ

2

12

v

u

u

u

u

t

(5)

To put the inter-year variations in perspective, MBE and RMSE

were normalised by the respective 30-year long-term monthly
mean value in each city, and the

findings are shown in

Fig. 4

. In

Harbin, MBE ranged from

6.6% (under-estimation) in 1995 to 5.6%

(over-estimation) in 1977, and RMSE from 3.3% in 1984 to 11.8% in

1977. These suggest that the estimated annual building energy use
in 1977 could be 5.6% different from the 30-year long-term mean
and the individual months could differ by 11.8%. The MBE and RMSE
for TMY were

2.4% and 4.7%, respectively, and for TPCY 1.5% and

2.5%. Both were near the lower ends of the variations indicating
that simulated results from TMY and TPCY tended to follow the
long-term mean more closely than the individual years. Similar
characteristics can be observed from the other four cities. It is
interesting to see that Harbin appeared to have larger MBE and
RMSE than the other cities, indicating larger variations (in terms of
climatic in

fluence on building energy use) from one year to another

in the severe cold climates. There also seemed to be a tendency for

J

F

M

A

M

J

J

A

S

O

N

D

200

400

600

800

1000

1200

1400

Bui

dl

in

g energy u

se (MWh)

Month

Harbin

J

F

M

A

M

J

J

A

S

O

N

D

300

400

500

600

700

800

Buidlin

g

ener

gy

use (MWh)

Month

Beijing

J

F

M

A

M

J

J

A

S

O

N

D

300

400

500

600

700

800

Buidl

in

g energy

use (MWh)

Month

Shanghai

J

F

M

A

M

J

J

A

S

O

N

D

300

400

500

600

700

Buidlin

g energy

use (MWh)

Month

Kunming

J

F

M

A

M

J

J

A

S

O

N

D

300

400

500

600

700

800

B

uidling energy use (

M

Wh)

Month

Hong Kong

Fig. 3. Comparison of total building energy use between TMY, TPCY and 30-year long-term mean for the

five cities.

L. Yang et al. / Energy 36 (2011) 6121

e6129

6126

the MBE and RMSE to decrease (i.e. less inter-year variations) as we
moved from colder climates in the north to warmer climates in the
south. The most important

finding was that TPCY had the smallest

MBE (Harbin 1.5%, Beijing 0.9%, Shanghai 0.2%, Kunming

0.4% and

Hong Kong 0.2%) and RMSE (Harbin 2.5%, Beijing 2.1%, Shanghai
1.2%, Kunming 0.9% and Hong Kong 1.1%). In terms of the ability to
follow the long-term monthly and annual building energy use
estimation, TPCY outperformed TMY in all

five cities. This has

-8

-4

0

4

8

12

16

TP

CY

E

rro

rs

(in

%

)

Year

71

75

80

85

90

95

00

TM

Y

Harbin

-8

-4

0

4

8

12

16

TP

C

Y

E

rro

rs

(in

%

)

Year

71

75

80

85

90

95

00

TMY

Beijing

-8

-4

0

4

8

12

16

TPC

Y

E

rro

rs

(in

%

)

Year

71

75

80

85

90

95

00

TM

Y

Shanghai

-8

-4

0

4

8

12

16

TP

C

Y

E

rro

rs

(in

%

)

Year

71

75

80

85

90

95

00

TM

Y

Kunming

-8

-4

0

4

8

12

16

TP

C

Y

Er

ro

rs

(i

n

%

)

Year

79

85

90

95

00

05

08

TM

Y

Hong Kong

Fig. 4. Summary of the mean bias error (MBE) and root mean square error (RMSE) for the

five cities.

Table 6
A summary of the 12 typical principal component months (TPCMs) for the

five cities in the 21st century (2001e2100) for low and medium forcing.

Harbin

Beijing

Shanghai

Kunming

Hong Kong

B1

A1B

B1

A1B

B1

A1B

B1

A1B

B1

A1B

Jan

2066

2023

2100

2013

2078

2040

2097

2065

2045

2061

Feb

2054

2043

2046

2047

2015

2078

2006

2055

2010

2022

Mar

2088

2058

2021

2042

2092

2064

2050

2080

2033

2058

Apr

2082

2035

2062

2050

2049

2043

2031

2027

2045

2017

May

2044

2050

2033

2061

2025

2042

2022

2027

2044

2039

Jun

2043

2021

2012

2037

2012

2042

2032

2047

2036

2034

Jul

2060

2054

2088

2051

2010

2078

2023

2040

2061

2055

Aug

2035

2043

2052

2057

2037

2076

2058

2044

2034

2045

Sep

2072

2055

2049

2057

2032

2036

2075

2045

2079

2082

Oct

2033

2056

2046

2032

2080

2077

2003

2082

2040

2086

Nov

2014

2048

2062

2058

2026

2017

2021

2050

2052

2061

Dec

2078

2092

2089

2059

2063

2038

2062

2030

2050

2057

Note: B1

¼ low forcing, A1B ¼ medium forcing.

L. Yang et al. / Energy 36 (2011) 6121

e6129

6127

demonstrated the difference between the present work and the
conventional TMY method.

7. Identifying TPCMs for the 21st century

To illustrate the application of the principal component

approach, an attempt was made to identify the 12 TPCMs for each of
the

five cities in the 21st century using predictions from general

circulation models (GCMs). Future weather conditions were
obtained from the World Climate Research Programme

’s (WCRP)

Coupled Model Intercomparison Project Phase 3 (CMIP3) multi-
model data set

[41]

. Details of data gathering and model selection

can be found in

[17,18]

. Brie

fly, there were five GCMs that had

archived monthly mean DBT, moisture content, and GSR. Predictions
from these

five GCMs were downloaded and analysed. These GCMs

included the BCCR-BCM2.0 (Norway), GISS-AOM (USA), INM-CM3.0
(Russia), MIROC3.2-H (Japan) and NCAR-CCSM3.0 (USA). They
covered predictions for the past 10 decades (1900

e1999) based on

known emissions and future years (2000

e2099 for NCAR-CCSM3.0

and BCCR-BCM2.0; and 2001

e2100 for GISS-AOM, INM-CM3.0 and

MIROC3.2-H) based on different emissions scenarios

[42]

. It was

found that MIROC3.2-H tended to perform well in temperature and
humidity but only average in solar radiation among the

five models

[17]

. In this study, MIROC3.2-H was selected for two reasons. Firstly,

temperature and humidity greatly affect the air-conditioning load,
particularly latent cooling in subtropical climates. Secondly, our
recent work on human bioclimate had found that MIROC3.2-H
tended to show the best agreement between measured data and
model predictions

[11]

.

Predictions from the MIROC3.2-H GCM were used in the PCA for

the 21st century (2001

e2100) for two scenarios

[41,42]

e SRES B1

(low forcing, rapid change towards a service and information
economy, peak global population in mid-21st century and decline
thereafter, introduction of clean and resource-ef

ficient technologies

(e.g. daylighting applications

[43]

), and emphasis on global solutions

to economic social and environmental sustainability), and SRES A1B
(medium forcing, very rapid economic growth, same population
trends as B1, convergence among regions with increased cultural
and social interactions, and technological emphasis on a balanced
mix of fossil and non-fossil energy resources (e.g. photovoltaic

[44]

)). Wet-bulb temperatures were determined from the corre-

sponding DBT and moisture content.

Table 6

shows a summary of

the TPCMs in the 21st century in the

five cities for the low and

medium forcing scenarios. It is interesting to observe that different

cities tend to have different years for the TPCMs. There are only two
exceptions among the 120 TPCMs

e Harbin and Hong Kong have the

same TPCMs, the year 2044 in May for low forcing and the year 2058
in March for medium forcing. This suggests that what is considered
typical (in terms of resembling the 100-year long-term average)
within one climate zone may not be typical in another. For low
forcing, most of the TPCMs occur only once or twice except 2033 and
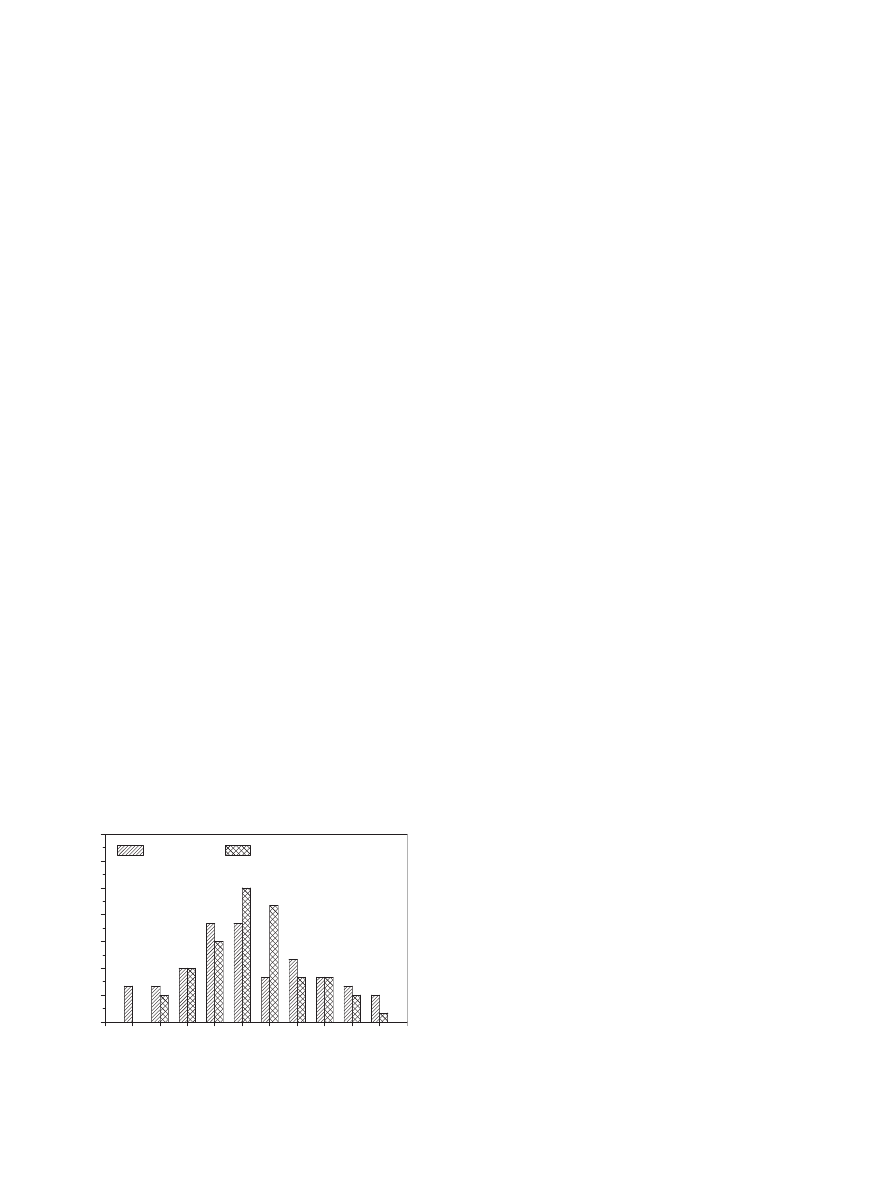
2062 which appear three times. To have an idea about the distri-
bution of TPCMs among the 100 years, the frequency of occurrence
of TPCMs within each decade during the 21st century was deter-
mined. A summary is shown in

Fig. 5

. Both the low and medium

forcing show

“normal” distributions with peaks centred around

2031

e2060. Medium forcing has larger peaks and tends to shift

towards the right (i.e. 2nd half of the 21st century).

8. Conclusions

Principal component analysis of 30-year long-term meteoro-

logical variables (dry-bulb temperature, wet-bulb temperature and
global solar radiation) was conducted. A typical weather year called
the typical principal component year (TPCY) was determined for
each of the

five major architectural climates e severe cold, cold, hot

summer and cold winter, mild, and hot summer and warm winter.
These were compared with the 30 individual years as well as the
widely used typical meteorological years (TMYs). In terms of the
monthly principal component Z and the monthly total building
energy consumption, both the TMY and TPCY followed the 30-year
long-term means quite closely. TPCY had the smallest mean bias
error (MBE) and root mean square error (RMSE) indicating its
ability to represent the long-term building energy use estimation.
The MBE was 1.5%, 0.9%, 0.2%,

0.4% and 0.2% in Harbin, Beijing,

Shanghai, Kunming and Hong Kong, respectively. This suggests that
predictions from the TPCY could be within 0.2%

e1.5% of the 30-year

long-term mean energy use estimation. To illustrate the application
of the principal component approach, an attempt was made to
identify the 12 TPCMs for each of the

five cities in the 21st century

using predictions from general circulation models (GCMs). We
believe the principal component analysis approach is a good
alternative to the conventional TMY and could have important
applications. The TPCY method would be useful in the regular (e.g.
every

five or 10 years) updating of existing typical weather years. It

can also be applied to studies on the impact of climate change on
energy use in the built environment in the 21st century involving
detailed hour-by-hour simulation. For instance, one can access the
archived monthly data for the three key meteorological variables
from general circulation models, analyse them and download the
required hourly weather data of the 12 typical months instead of
the total 1200 months in the 21st century. Although this study only
focused on the major climates within China, it is envisaged that the
approach and analysis could be applied to other locations with
similar or different climatic conditions.

Acknowledgements

The work described in this paper was fully supported by a Public

Policy Research Exercise grant from the Research Grants Council of
the Hong Kong Special Administrative Region, China [Project no.
9056002 (CityU 1011-PPR-10)]. K.K.W. Wan was supported by a City
University of Hong Kong Studentship. Measured weather data were
obtained from the China National Meteorological Centre in Beijing
and the Hong Kong Observatory of the Hong Kong SAR. We
acknowledge the modelling groups, the Program for Climate Model
Diagnosis and Intercomparison (PCMDI) and the WCRP

’s Working

Group on Coupled Modelling (WGCM) for their roles in making

20

01

-20

10

20

11

-20

20

20

21

-20

30

20

31

-20

40

20

41

-20

50

20

51

-20

60

20

61

-20

70

20

71

-20

80

20

81

-20

90

20

91

-21

00

0

5

10

15

20

25

30

35

Frequency of occurence (%)

Periods

B1 low forcing

A1B medium forcing

Fig. 5. Frequency of occurrence of typical principal component months within the ten
10-year periods in the 21st century.

L. Yang et al. / Energy 36 (2011) 6121

e6129

6128

available the WCRP CMIP3 multi-model data set. Support of this data
set is provided by the Of

fice of Science, U.S. Department of Energy.

References

[1] Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, et al., editors.

Climate change 2007: the physical science basis. Contribution of the working
group I to the fourth assessment report of the intergovernmental panel on
climate change. Cambridge: Cambridge University Press; 2007.

[2] Levine M, Urge-Vorsatz D, Blok K, Geng L, Harvey D, Lang S, et al. Residential

and commercial buildings. In: Metz B, Davidson OR, Bosch PR, Dave R,
Meyer LA, editors. Climate change 2007: Mitigation. contribution of working
group III to the fourth assessment report of the intergovernmental panel on
climate change. Cambridge: Cambridge University Press; 2007. p. 387

e446.

[3] Levermore GJ. A review of the IPCC assessment report four, part 1: the IPCC

process and greenhouse gas emission trends from buildings worldwide. Build
Serv Eng Res Technol 2008;29:349

e61.

[4] Lang S. Current situation and progress of energy ef

ficiency design standards in

buildings in China. Refrig Air Cond Electr Power Mach 2002;23:1

e6. in Chinese.

[5] Yao R, Li B, Steemers K. Energy policy and standard for built environment in

China. Renew Energy 2005;30:1973

e88.

[6] He J, Deng J, Su M. CO

2

emission from China

’s energy sector and strategy for its

control. Energy 2010;35:4494

e8.

[7] Ma L, Liu P, Fu F, Li Z, Ni W. Integrated energy strategy for the sustainable

development of China. Energy 2011;36:1143

e54.

[8] Zhang N, Lior N, Jin H. The energy situation and its sustainable development

strategy in China. Energy 2011;36:3639

e49.

[9] Lam JC, Wan KKW, Yang L. Sensitivity analysis and energy conservation

measures implications. Energy Convers Manage 2008;49:3170

e7.

[10] Wang Z, Ding Y, He J, Yu J. An updating analysis of the climate change in China

in recent 50 years. ACTA Meteorol Sinica 2004;62:228

e36. in Chinese.

[11] Wan KKW, Wong SL, Yang L, Lam JC. An analysis of the bioclimates in different

climates and implications for the built environment in China. Build Environ
2010;45:1312

e8.

[12] Wan KKW, Li DHW, Yang L, Lam JC. Climate classi

fications and building

energy use implications in China. Energy Build 2010;42:1463

e71.

[13] Lam JC, Li DHW. Daylighting and energy analysis for air-conditioned of

fice

buildings. Energy 1998;23:79

e89.

[14] Li DHW, Lam JC, Wong SL. Daylighting and its implications to overall thermal

transfer value determination. Energy 2002;27:991

e1008.

[15] Lam JC, Wan KKW, Liu D, Tsang CL. Multiple regression models for energy use

in air-conditioned of

fice buildings in different climates. Energy Convers

Manage 2010;51:2692

e7.

[16] Lam JC, Tang HL, Li DHW. Seasonal variations in residential and commercial

sector electricity consumption in Hong Kong. Energy 2008;33:513

e23.

[17] Lam JC, Wan KKW, Lam TNT, Wong SL. An analysis of future building energy

use in subtropical Hong Kong. Energy 2010;35:1482

e90.

[18] Wan KKW, Li DHW, Lam JC. Assessment of climate change impact on building

energy use and mitigation measures in subtropical climates. Energy 2011;36:
1404

e14.

[19] Zhao S. Physical geography of China. New York: Van Nostrand Reinhold; 1986.
[20] Zhang J, Lin Z. Climate of China. New York: John Wiley & Sons; 1992.
[21] Ministry of Construction of P.R.C. Thermal design code for civil building (GB

50176-93). Beijing: China Planning Press; 1993. in Chinese.

[22] Lam JC, Hui SCM, Chan ALS. A statistical approach to the development of

a typical meteorological year for Hong Kong. Architect Sci Rev 1996;39:
201

e9.

[23] Ecevit A, Akinoglu BG, Aksoy B. Generation of a typical meteorological year

using sunshine duration data. Energy 2002;27:947

e54.

[24] Yang L, Lam JC, Liu J. An analysis of the typical meteorological years in

different climates in China. Energy Convers Manage 2007;48:654

e68.

[25] Hall IJ, Prairie RR, Anderson HE, Boes EC. Generation of typical meteorological

years for 26 SOLMET stations. SAND 78

e1601. Albuquerque, New Mexico:

Sandia National Laboratories; 1978.

[26] Marion W, Urban K. User manual for TMY2. Colorado: National Renewable

Energy Laboratory; 1995.

[27] Finkelstein JM, Schafer RE. Improved goodness-of-

fit tests. Biometrika 1971;

58:641

e5.

[28] Crow LW. Development of hourly data for weather year for energy calcula-

tions (WYEC), including solar data, at 21 stations throughout the U.S. ASHRAE
Trans 1981;87:896

e906.

[29] Wilks DS. Statistical method in the atmospheric sciences: an introduction. San

Diego: Academic Press; 1995.

[30] Storch HV, Zwiers FW. Statistical analysis in climate research. Cambridge:

Cambridge University Press; 1999.

[31] Lam JC. Energy analysis of commercial buildings in subtropical climates. Build

Environ 2000;35:19

e26.

[32] Bojic M, Yik F, Leung W. Thermal insulation of cooled spaces in high rise

residential buildings in Hong Kong. Energy Convers Manage 2002;43:
165

e83.

[33] Wan KKW, Cheung KL, Yang L, Lam JC. A new variable for climate change

study and implications for the built environment. Renew Energy 2009;34:
916

e9.

[34] Kalkstein LS, Tan G, Skindlov JA. An evaluation of three clustering procedures

for use in synoptic climatological classi

fication. J Clim Appl Meteorol 1987;26:

717

e30.

[35] Ladd JW, Driscoll DM. A comparison of objective and subjective means of

weather typing: an example from West Texas. J Appl Meteorol 1980;19:
691

e704.

[36] DOE-2 Supplement, Version 2.1E, LBL-34947. Lawrence Berkeley National

Laboratory, University of California; 1993.

[37] Code for Design of Heating Ventilation and Air-conditioning (GB 50019-2003).

Beijing: China Planning Press; 2003. in Chinese.

[38] Design Standard for Energy Ef

ficiency of Public Buildings (GB 50189-2005).

Beijing: China Architecture and Building Press; 2005. in Chinese.

[39] Amendments to the Code of Practice for Overall Thermal Transfer Value in

Buildings. Hong Kong: Buildings Department; 2000.

[40] Performance-based Building Energy Code. Hong Kong: Electrical and

mechanical Services Department; 2007.

[41] Meehl GA, Covey C, Delworth T, Latif M, McAvaney B, Mitchell JFB, et al. The

WCRP CMIP3 multi-model dataset: a new era in climate change research. Bull
Am Meteorol Soc 2007;88:1383

e94.

[42] IPCC Working Group III. In: Nakicenovic N, Swart S, editors. Special report on

emissions scenarios. Cambridge: Cambridge University Press; 2000.

[43] Chel A, Tiwari GN, Singh HN. A modi

fied model for estimation of daylight

factor for skylight integrated with dome roof structure of mud-house in New
Delhi (India). Appl Energy 2010;87:3030

e50.

[44] Chel A, Tiwari GN. A case study of a typical 2.32 kWp stand-alone photovoltaic

(SAPV) in composite climate of New Delhi (India). Appl Energy 2011;88:
1415

e26.

L. Yang et al. / Energy 36 (2011) 6121

e6129

6129