1.
Sprawdź, czy trójkąt o bokach długości
a)
3, 4, 5,
b)
5, 12, 13
jest prostokątny. Jeśli tak, oblicz promień R okręgu opisanego na tym trójkącie, promień r okręgu wpi-
sanego w ten trójkąt, długość wysokości h poprowadzonej z wierzchołka kąta prostego, pole P trójkąta.
2.
Oblicz promień okręgu wpisanego i opisanego na trójkącie o bokach: 10, 13, 13. Oblicz pole trójką-
ta.
3.
Na okręgu o promieniu
2
r
=
opisano trójkąt prostokątny, którego przeciwprostokątna c ma długość
10. Oblicz pole P i obwód L tego trójkąta.
4.
Dany jest trójkąt o wierzchołkach:
(
)
1, 3
A
= −
,
( )
3, 5
B
=
,
(
)
3, 5
C
=
−
.
5.
Uzasadnij, że jest to trójkąt prostokątny.
6.
Wyznacz równanie okręgu opisanego na tym trójkącie.
7.
Jednym z boków trójkąta równobocznego jest odcinek AB, gdzie
(
)
2, 5
A
= −
,
(
)
4, 3
B
=
−
. Oblicz
pole tego trójkąta. Oblicz promień okręgu opisanego na tym trójkącie i promień okręgu wpisanego w
ten trójkąt.
8.
Dany jest trójkąt o wierzchołkach:
(
)
6,1
A
= −
,
(
)
2, 5
B
= − −
,
( )
5, 4
C
=
. Wyznacz pole trójkąta
ABC. *Wyznacz promień okręgu wpisanego w ten trójkąt.
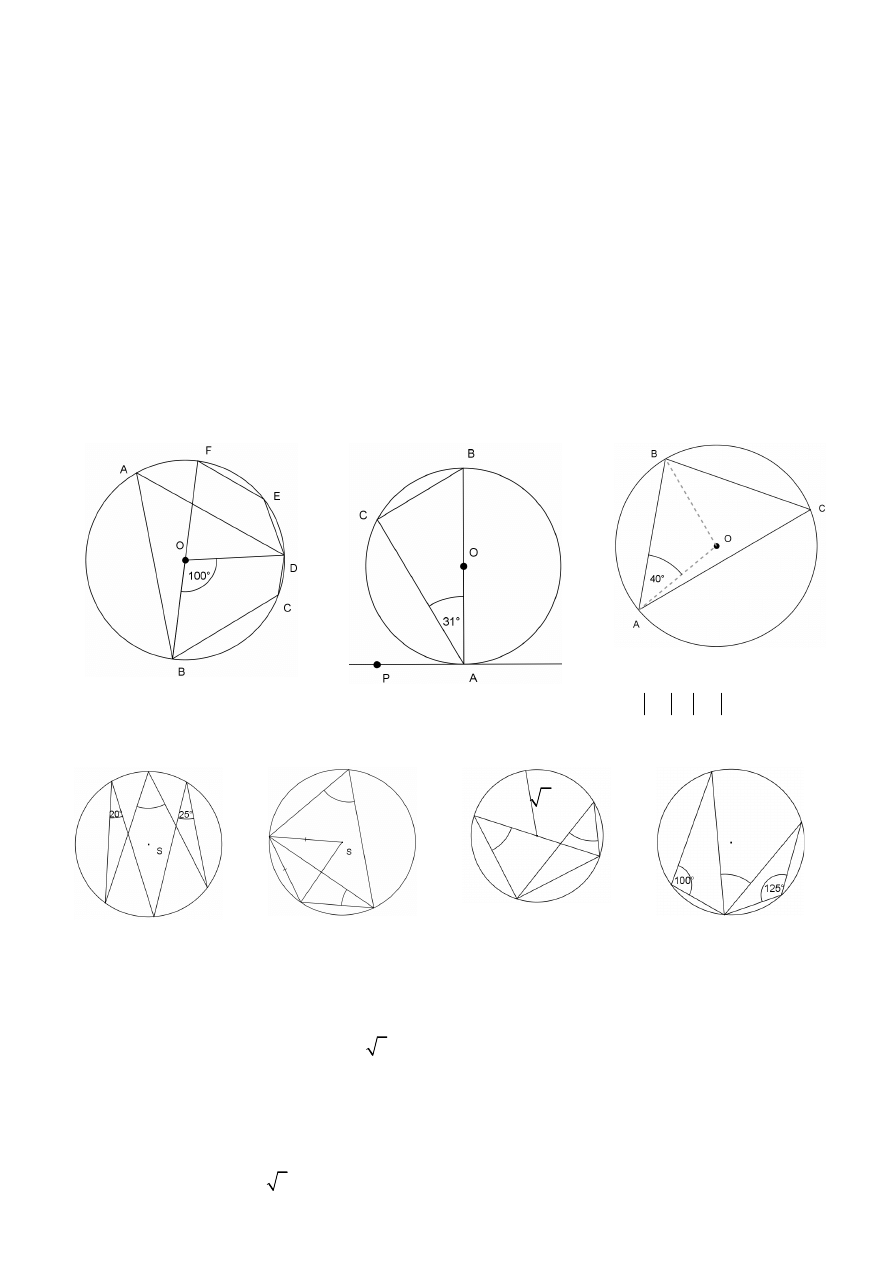
9.
a)
Wyznacz miary kątów:
BAD
∢
,
BCD
∢
i
DEF
∢
.
b)
Wyznacz kąty:
PAC
∢
,
ABC
∢
.
c)
Oblicz miary kątów trój-
kąta ABC, wiedząc że
AB
BC
=
.
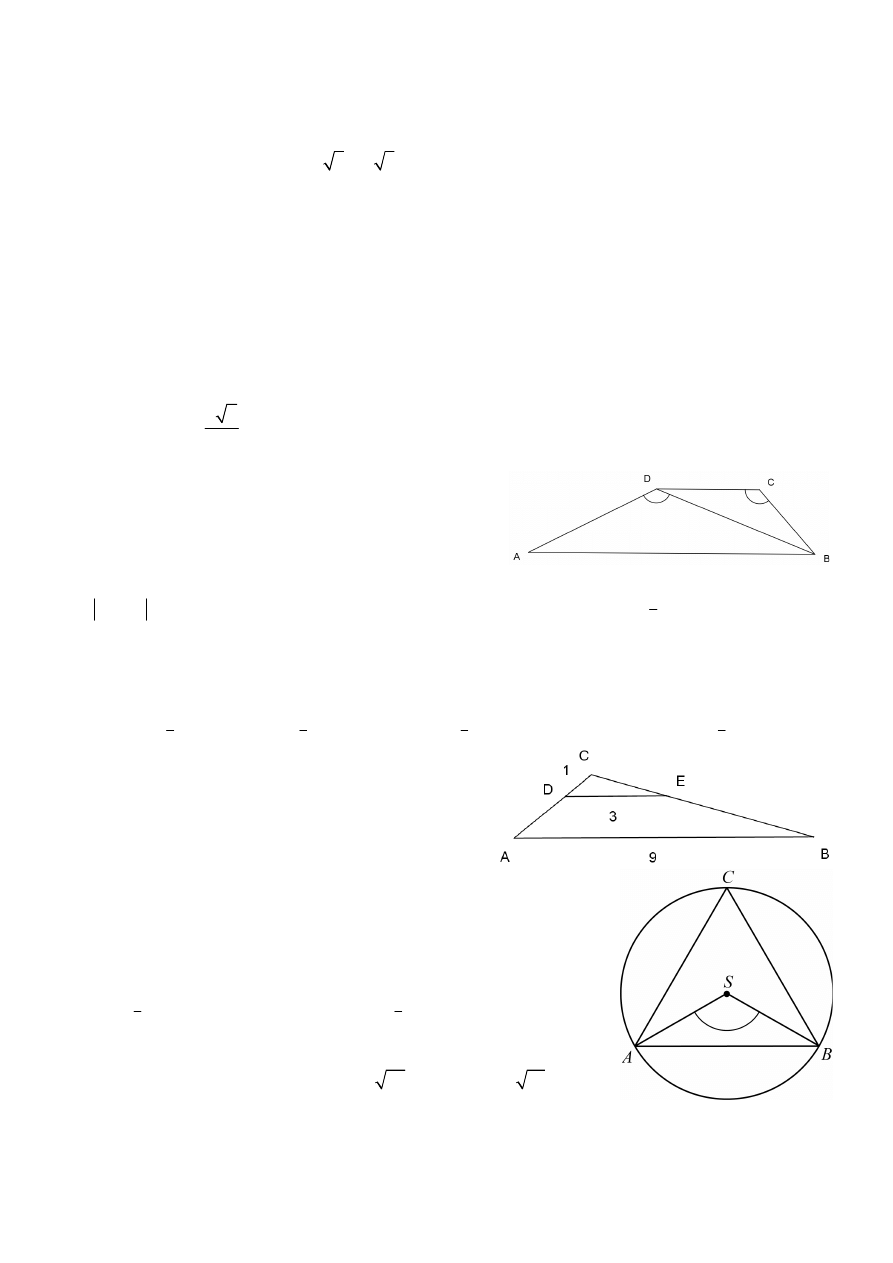
10.
Oblicz miary kątów oznaczonych literami:
a)
b)
c)
d)
11.
W kwadrat o boku
12
a
cm
=
wpisano okrąg, a w ten okrąg wpisano trójkąt równoboczny. Oblicz
stosunek pól kwadratu do trójkąta.
12.
Na kwadracie o boku
12
a
cm
=
opisano okrąg, a na tym okręgu opisano trójkąt równoboczny. Ob-
licz stosunek pól kwadratu do trójkąta.
13.
Napisz równanie okręgu o środku
( )
2, 4
S
wiedząc, że do tego okręgu należy punkt
( )
1,1
A
=
.
14.
Napisz równanie okręgu o promieniu 5 stycznego do prostej
2
1
0
x
y
−
− =
w punkcie
( )
3,1
A
=
.
15.
Przyprostokątne trójkąta prostokątnego mają długości 6 i 12. Oblicz długość promienia okręgu
stycznego do obu przyprostokątnych o środku należącym do przeciwprostokątnej.
16.
W prostokącie połączono środki sąsiednich boków i otrzymano romb, którego obwód jest równy 20,
a pole 24. oblicz długości boków prostokąta.
17.
Obwód rombu jest równy 20, a suma przekątnych 14. Oblicz pole i wysokość rombu.
18.
W rombie o obwodzie 8 5 długości przekątnych różnią się o 4. Oblicz ich długości.
ϕ
δ
ω
2
2
β
γ
r
r
α
19.
W półokrąg o promieniu
8
r
=
wpisano prostokąt ABCD , którego wierzchołki A i B leżą na średni-
cy tego okręgu, a wierzchołki C i D na półokręgu. Oblicz pole prostokąta wiedząc, że stosunek dłu-
gości jego boków AB i BC jest równy 2.
20.
Kąt ostry równoległoboku ma miarę 60
°
. Odległość punktu przecięcia się przekątnych równoległo-
boku od jego boków są równe 5 3 i 2 3 . Oblicz pole i obwód tego równoległoboku.
Zadania z matur na poziomie podstawowym:
(maj 2008 r.)
21.
Prosta o równaniu 5
4
10
0
x
y
+
−
=
przecina oś Ox układu współrzędnych w punkcie A oraz oś Oy w
punkcie B . Oblicz współrzędne wszystkich punktów C leżących na osi Ox i takich, że trójkąt ABC ma
pole równe 35.
22.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą pod-
stawą kąty o miarach 30
° i 45°. Oblicz wysokość tego trapezu.
23.
Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa
α
.
a)
Uzasadnij, że spełniona jest nierówność sin
tg
0
α
α
−
<
.
b)
Dla
2 2
sin
3
α
=
oblicz wartość wyrażenia
3
2
cos
cos
sin
α
α
α
+
⋅
.
(maj 2009 r.)
24.
W trapezie ABCD długość podstawy CD jest równa 18 ,
a długości ramion trapezu AD i BC są odpowiednio
równe 25 i 15. Kąty ADB i DCB, zaznaczone na rysun-
ku, mają równe miary. Oblicz obwód tego trapezu.
25.
Punkty
(
)
0,10
B
=
i
( )
0, 0
O
=
są wierzchołkami trójkąta prostokątnego OAB, w którym
90
OAB
= °
∢
. Przyprostokątna OA zawiera się w prostej o równaniu
1
2
y
x
=
. Oblicz współrzędne
punktu A i długość przyprostokątnej OA.
(maj 2010 r.)
26.
Prosta o równaniu
(
)
2
3
3
y
x
m
= − +
+
przecina w układzie współrzędnych oś Oy w punkcie
( )
0, 2
.
Wtedy
A.
2
3
m
= −
B.
1
3
m
= −
C.
1
3
m
=
D.
5
3
m
=
27.
Odcinki AB i DE są równoległe. Długości odcinków
CD
, DE i AB są odpowiednio równe 1, 3 i 9. Długość
odcinka AD jest równa
A.
2
B.
3
C.
5
D.
6
28.
Liczba przekątnych siedmiokąta foremnego wynosi:
A.
7
B.
14
C.
21
D.
28
29.
Punkty A, B, C leżące na okręgu o środku S są wierzchołkami trójkąta
równobocznego. Miara zaznaczonego na rysunku kąta środkowego
ASB
jest równa
A.
120
°
B.
90
°
C.
60
°
D.
30
°
30.
Współczynnik kierunkowy prostej równoległej do prostej o równaniu
3
5
y
x
= − +
jest równy:
A.
1
3
−
B.
3
−
C.
1
3
D.
3
31.
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma dłu-
gość 5. Wysokość opuszczona na podstawę ma długość
A.
3
B.
4
C.
34
D.
61
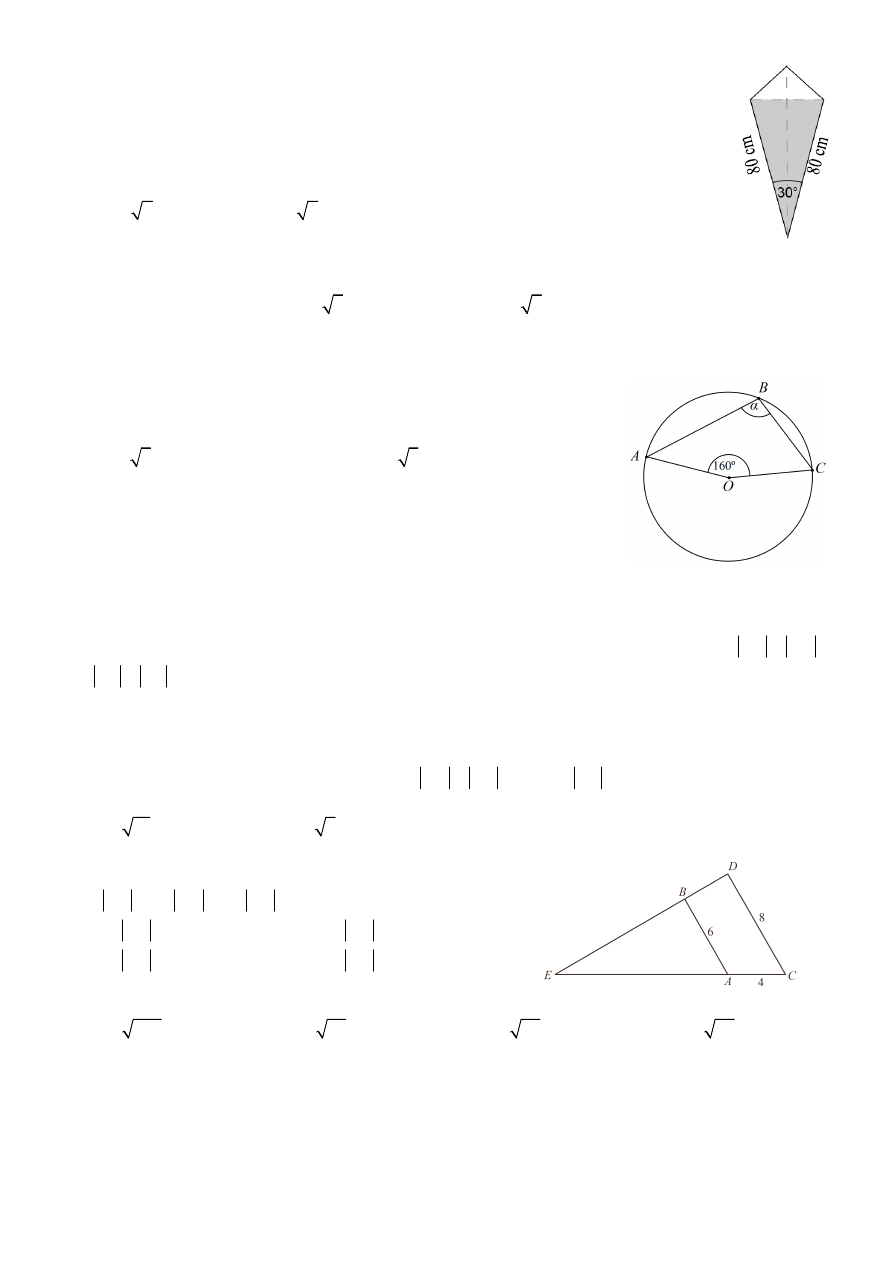
32.
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest
równa
A.
2
3200cm
B.
2
6400cm
C.
2
1600cm
D.
2
800cm
33.
Wskaż równanie okręgu o promieniu 6.
A.
2
2
3
x
y
+
=
B.
2
2
6
x
y
+
=
C.
2
2
12
x
y
+
=
D.
2
2
36
x
y
+
=
34.
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa:
A.
4 2
B.
2 2
C.
8
D.
4
35.
Punkty
(
)
5; 2
A
= −
i
(
)
3; 2
B
=
−
są wierzchołkami trójkąta równobocznego ABC. Obwód tego trójką-
ta jest równy
A.
30
B.
4 5
C.
12 5
D.
36
36.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny.
Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
(maj 2011 r.)
37.
Punkt O jest środkiem okręgu. Kąt wpisany
α
ma miarę
A.
80
°
B.
100
°
C.
110
°
D.
120
°
38.
Wysokość rombu o boku długości 6 i kącie ostrym 60
°
jest równa:
A.
3 3
B.
3
C.
6 3
D.
6
39.
Prosta k ma równanie
2
3
y
x
=
−
. Wskaż równanie prostej l równole-
głej do prostej k i przechodzącej przez punkt
(
)
2;1
D
= −
.
A.
2
3
y
x
= − +
B.
2
1
y
x
=
+
C.
2
5
y
x
=
+
D.
1
y
x
= − +
40.
Styczną do okręgu
(
)
2
2
1
4
0
x
y
−
+
− =
jest prosta o równaniu
A.
1
x
=
B.
3
x
=
C.
0
y
=
D.
4
y
=
41.
Dany jest czworokąt ABCD, w którym AB CD
. Na boku BC wybrano taki punkt E, że
EC
CD
=
i
EB
BA
=
. Wykaż, że kąt AED jest prosty.
42.
Okrąg o środku w punkcie
( )
3;7
S
=
jest styczny do prostej o równaniu
2
3
y
x
=
−
. Oblicz współ-
rzędne punktu styczności.
(listopad 2009 r.)
43.
W trójkącie równoramiennym ABC dane są
7
AC
BC
=
=
oraz
12
AB
=
. Wysokość opuszczona z
wierzchołka C jest równa
A.
13
B.
5
C.
1
D.
5
44.
Oblicz długość odcinka AE wiedząc, że AB CD
i
6
AB
=
,
4
AC
=
,
8
CD
=
.
A.
2
AE
=
B.
4
AE
=
C.
6
AE
=
D.
12
AE
=
45.
Dane są punkty
(
)
2;3
A
= −
oraz
( )
4;6
B
=
. Długość odcinka AB jest równa
A.
208
B.
52
C.
45
D.
40
46.
Promień okręgu o równaniu
(
)
2
2
1
16
x
y
−
+
=
jest równy
A.
1
B.
2
C.
3
D.
4
47.
W układzie współrzędnych na płaszczyźnie punkty
( )
2;5
A
=
i
( )
6;7
C
=
są przeciwległymi wierz-
chołkami kwadratu ABCD. Wyznacz równanie prostej BD.
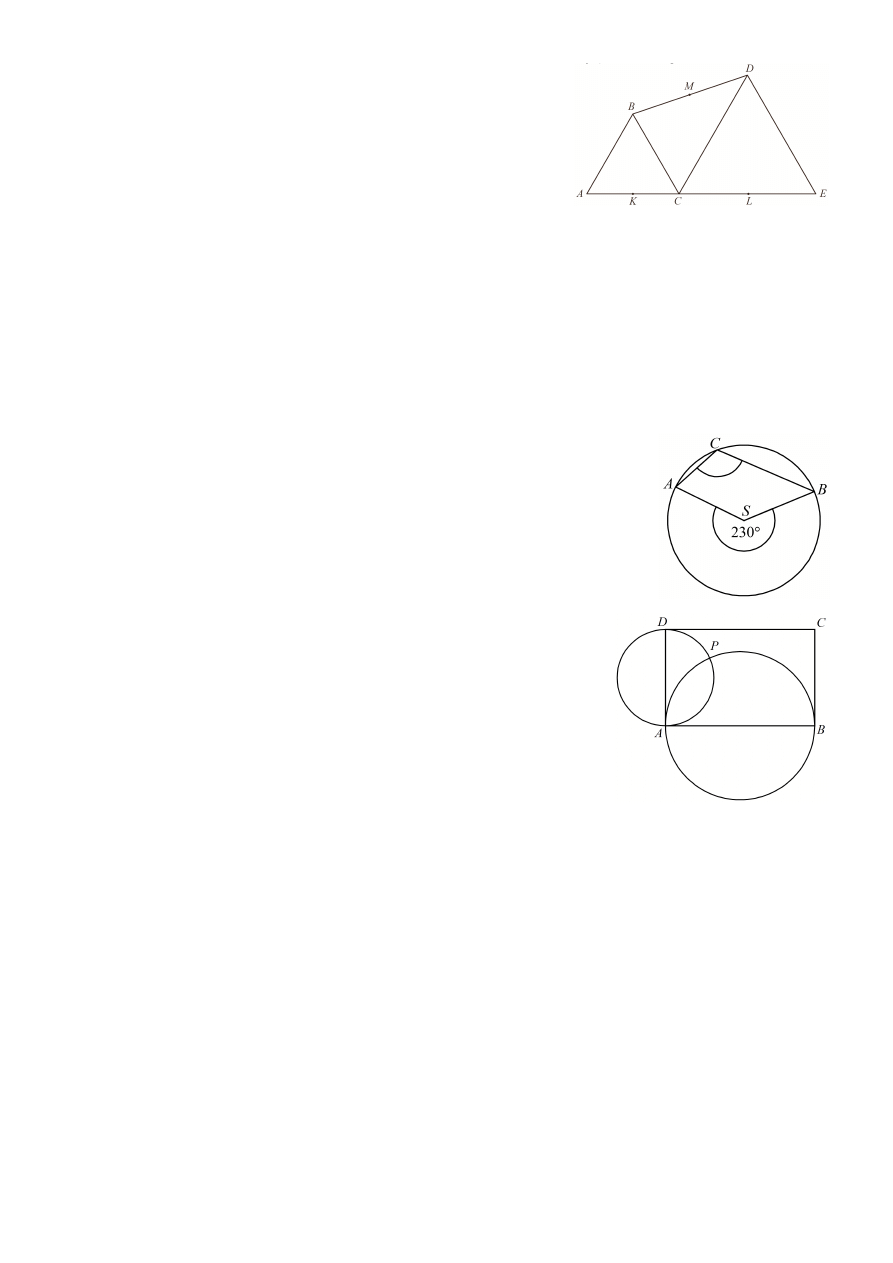
48.
Trójkąty ABC i CDE są równoboczne. Punkty A, C i E leżą na
jednej prostej. Punkty K, L, M są środkami odcinków AC, CE i
BD (zobacz rysunek). Wykaż, że punkty K, L i M są wierzchoł-
kami trójkąta równobocznego.
49.
Pole trójkąta prostokątnego jest równe
2
60cm . Jedna przypro-
stokątna jest o 7 cm dłuższa od drugiej. Oblicz długość prze-
ciwprostokątnej tego trójkąta.
50.
Punkty
( )
2; 0
A
=
i
(
)
12; 0
B
=
są wierzchołkami trójkąta prostokątnego ABC o przeciwprostokątnej
AB. Wierzchołek C leży na prostej o równaniu y
x
=
. Oblicz współrzędne punktu C.
(listopad 2010 r.)
51.
Ogród ma kształt prostokąta o bokach długości 20 m i 40 m. Na dwóch końcach przekątnej tego pro-
stokąta wbito słupki. Odległość między tymi słupkami jest
A.
równa 40 m
B.
większa niż 50 m
C.
większa niż 40 m i mniejsza niż 45 m
D.
większa niż 45 m i mniejsza niż 50 m
52.
Pionowy słupek o wysokości 90 cm rzuca cień o długości 60 cm. W tej samej chwili stojąca obok
wieża rzuca cień długości 12 m. Jaka jest wysokość wieży?
A.
18 m
B.
8 m
C.
9 m
D.
16 m
53.
Punkty A, B i C leżą na okręgu o środku S (zobacz rysunek). Miara zazna-
czonego kąta wpisanego ACB jest równa
A.
65
°
B.
100
°
C.
115
°
D.
130
°
54.
Dane są punkty
( )
2;1
S
=
,
( )
6; 4
M
=
. Równanie okręgu o środku S
i przechodzącego przez punkt M ma postać:
A.
(
) (
)
2
2
2
1
5
x
y
−
+
−
=
B.
(
) (
)
2
2
2
1
25
x
y
−
+
−
=
C.
(
) (
)
2
2
6
4
5
x
y
−
+
−
=
D.
(
) (
)
2
2
6
4
25
x
y
−
+
−
=
55.
Dany jest prostokąt ABCD. Okręgi o średnicach AB i AD przecinają
się w punktach A i P (zobacz rysunek). Wykaż, że punkty B, P i D le-
żą
na jednej prostej.
56.
Przeciwprostokątna trójkąta prostokątnego jest dłuższa od jednej
przyprostokątnej o 1 cm i od drugiej przyprostokątnej o 32 cm. Oblicz
długości boków tego trójkąta.
57.
Punkty
( )
1;5
A
=
,
(
)
14;31
B
=
(
)
4;31
C
=
są wierzchołkami trójkąta.
Prosta zawierająca wysokość tego trójkąta poprowadzona z wierz-
chołka C przecina prostą AB w punkcie D. Oblicz długość odcinka
BD.