Zasada zachowania energii

Fizyka I (B+C)

Wykład XIV:

•

Praca, siły zachowawcze i energia potencjalna

•

Energia kinetyczna i zasada zachowania energii

•

Zderzenia elastyczne

Praca i energia

F

F

F

dr

Q

P

n

t

Praca

Siła

~

F

działa na punkt materialny P

Praca jak ˛

a wykonuje siła przy przesuni˛eciu P o

d~

r

dW

= ~

F · d~

r

= F cos θds = F

t

ds

Siły prostopadłe do przesuni˛ecia nie wykonuj ˛

a pracy!

siła Lorenza, siła Coriolisa, siły reakcji wi˛ezów...

Praca siły

~

F

(~

r

)

na drodze mi˛edzy

A

i

B

W

AB

=

B

Z

A

~

F

(~

r

) · d~

r

A.F. ˙Zarnecki

Wykład XIV

1

Praca i energia

Praca

W ogólnym przypadku praca

W

AB

jak ˛

a wykonujemy

podczas ruchu punktu z

A

do

B

mo˙ze zale˙ze´c od:

•

przebytej drogi l

np. praca sił tarcia b˛edzie proporcjonalna do l

•

toru ruchu

np. je´sli siły oporu zale˙z ˛

a od wyboru toru

•

pr˛edko´sci

siły oporu w o´srodku zale˙z ˛

a od pr˛edko´sci

•

czasu

je´sli działaj ˛

ace siły zale˙z ˛

a od czasu

A.F. ˙Zarnecki

Wykład XIV

2

Praca i energia

Energia potencjalna

Siła

~

F

(~

r

)

jest

zachowawcza

(konserwatywna), je´sli praca przez ni ˛

a wykonana

zale˙zy tylko od

poło˙zenia

punktów pocz ˛

atkowego (

A

) i ko ´ncowego (

B

)

⇒

mo˙zna j ˛

a wyrazi´c przez zmian˛e

energii potencjalnej

W

AB

=

B

Z

A

~

F

(~

r

) · d~

r

= E

p

(~

r

A

) − E

p

(~

r

B

)

= −∆E

p

Siła zachowawcza nie mo˙ze zale˙ze´c od czasu ani od pr˛edko´sci.

Je´sli droga jest zamkni˛eta to praca jest równa zeru

A

Z

A

~

F

(~

r

) · d~

r

=

I

~

F

(~

r

)d~

r

= 0

~

F

A.F. ˙Zarnecki

Wykład XIV

3

Praca i energia

Przykład:

Ruch w jednorodnym polu grawitacyjnym. Siła ci˛e˙zko´sci

~

F

= m ~

g

= m (0, −g, 0)

B

Z

A

~

F

(~

r

) · d~

r

= ~

F

B

Z

A

d~

r

= ~

F

(~

r

B

− ~

r

A

) = −m ~

g

(~

r

A

− ~

r

B

) = m g (y

A

− y

B

)

⇒

energia potencjalna dla jednorodnego pola grawitacyjnego

E

p

(~

r

) = −m ~

g ~

r

= m g y

Siłami zachowawczymi s ˛

a te˙z wszystkie siły centralne, zale˙zne tylko od odległo´sci

~

F

= F (r) ·~i

r

siła kulombowska, siła grawitacyjna, siły spr˛e˙zysto´sci...

A.F. ˙Zarnecki

Wykład XIV

4

Praca i energia

Gradient

Gradient wskazuje

kierunek

w którym

nast˛epuje

najwi˛eksza zmiana

warto´sci

funkcji skalarnej f(x, y, z).

Warto´s´c gradientu odpowiada

warto´sci

pochodnej

funkcji f(x, y, z) wzdłu˙z tego

kierunku.

grad f = ~∇f = ~i

x

∂f

∂x

+ ~i

y

∂f

∂y

+ ~i

z

∂f

∂z

=

∂f

∂x

,

∂f

∂y

,

∂f

∂z

!

⇒

~

∇ = ~i

x

∂

∂x

+ ~i

y

∂

∂y

+ ~i

z

∂

∂z

~

∇f = ~i

n

∂f

∂n

~

n

f

!

"

#

A.F. ˙Zarnecki

Wykład XIV

5

Praca i energia

Siła a energia potencjalna

Praca wykonana przy infintezymalnym przesuni˛eciu

d~

r

= (dx, dy, dz)

dW

= ~

F

(~

r

) · d~

r

= − dE

p

$%

&

'

(

')

(

)

*

+

&

&

,.-

/

)

(

0

1

'

2

(

)

1

⇒

= −

∂E

p

∂x

dx −

∂E

p

∂y

dy −

∂E

p

∂z

dz

Otrzymujemy:

~

F

= − ~

∇E

p

Znajomo´s´c potencjału siły zachowawczej jest rownowa˙zna znajomo´sci samej siły.

Energia potencjalna jest okre´slona z dokładno´sci ˛

a do stałej, istotne s ˛

a tylko jej zmiany.

A.F. ˙Zarnecki

Wykład XIV

6

Praca i energia

Energia kinetyczna

Praca jak ˛

a wykonuje siła

~

F

przy przesuni˛eciu P o

ds

dW

= F

t

ds

= m

a

t

ds

= m

dv

dt

ds

dv

dt

ds

= dv

ds

dt

⇒

= m

ds

dt

dv

= m

v

dv

Praca siły

~

F

(~

r

)

na drodze mi˛edzy

A

i

B

W

AB

=

B

Z

A

F

t

(s) · ds =

B

Z

A

mv dv

=

mv

2

B

2

−

mv

2

A

2

=

E

B

k

− E

A

k

= ∆E

k

Niezale˙znie od postaci siły ~

F

i drogi

na ciało nie działaj ˛

a inne siły, układ inercjalny

praca siły jest równa zmianie energii kinetycznej ciała

E

k

=

mv

2

2

A.F. ˙Zarnecki

Wykład XIV

7

Zasada zachowania energii

Zasada zachowania energii

Praca siły zachowawczej

~

F

(~

r

)

pomi˛edzy

A

i

B

W

AB

=

B

Z

A

~

F

(~

r

) · d~

r

=

E

A

p

− E

B

p

Z drugiej strony, praca siły działaj ˛

acej na ciało:

W

AB

=

E

B

k

− E

A

k

⇒

E

B

k

− E

A

k

= E

A

p

− E

B

p

⇒

E

B

k

+ E

B

p

= E

A

k

+ E

A

p

⇒

E

= E

p

+ E

k

=

34

5

67

W ruchu pod działaniem

sił zachowawczych

energia całkowita

jest

zachowana

.

A.F. ˙Zarnecki

Wykład XIV

8

Zasada zachowania energii

Wahadło Galileusza

Wysoko´s´c na jak ˛

a wznosi si˛e wahadło

nie zmienia si˛e przy zmianie długo´sci nici:

h

E

p

+ E

k

= E =

89

:

;<

E

k

= 0

⇒

m g h

= E

siły reakcji wi˛ezów nie wykonuj ˛

a pracy

Koło Maxwella

Przemiana energii potencjalnej w
energi˛e kinetyczn ˛

a ruchu obrotowego.

A.F. ˙Zarnecki

Wykład XIV

9

Zasada zachowania energii

Spadek swobodny

V

h

g

W jednorodnym polu ~g
ciało spada swobodnie z
wysoko´sci

h

(~v(0) = 0).

Pr˛edko´s´c ko´ncowa

z za-

sady zachowania energii:

∆E

k

= −∆E

p

m v

2

2

= m g h

v

=

q

2 g h

V

h

g

Tak ˛

a sam ˛

a pr˛edko´s´c uzyska wahadło

puszczone z wysoko´sci

h

A.F. ˙Zarnecki

Wykład XIV

10

Zderzenia

Poprzednio rozpatrywali´smy zderzenia ciał z punktu
widzenia

zasady zachowania p˛edu

(i momentu p˛edu)

zasada zachowania p˛edu jest zawsze bezwzgl˛ednie spełniona

Czy zachowana jest energia kinetyczna ?

TAK

- je´sli działaj ˛

ace siły maj ˛

a charakter zachowawczy

siły kulombowskie, siły sp˛e˙zysto´sci

∆E

p

= 0

⇒

∆E

k

= 0

NIE

- je´sli mamy wkład sił niezachowawczych

w wyniku zderzenia nast˛epuj ˛

a trwałe zmiany

(np. odkształcenia) w zderzaj ˛

acych si˛e ciałach

A.F. ˙Zarnecki

Wykład XIV

11

Zderzenia

Zderzenia spr˛e˙zyste

Przypadek jednowymiarowy:

V

1

V =0

2

M

2

M

1

V’

V’

1

2

M

2

M

1

Z zasad zachowania:

=.>

=@?

A

BC

p

:

m

1

V

0

1

+ m

2

V

0

2

= m

1

V

1

E

:

m

1

V

02

1

2

+

m

2

V

02

2

2

=

m

1

V

2

1

2

Przekształcamy:

p

:

m

2

V

0

2

= m

1

(V

1

− V

0

1

)

E

:

m

2

V

02

2

= m

1

(V

2

1

− V

02

1

)

= m

1

(V

1

− V

0

1

)(V

1

+ V

0

1

)

⇒

V

0

2

= V

1

+ V

0

1

, albo

V

0

2

− V

0

1

= V

1

warto´s´c bezwzgl˛edna pr˛edko´sci wzgl˛ednej przed i po zderzeniu jest taka sama

A.F. ˙Zarnecki

Wykład XIV

12

Zderzenia

Zderzenia spr˛e˙zyste

Przekształcaj ˛ac dalej otrzymujemy:

m

2

(V

1

+ V

0

1

) = m

1

(V

1

− V

0

1

)

⇒

V

0

1

(m

1

+ m

2

) = V

1

(m

1

− m

2

)

Ostatecznie:

V

0

1

=

m

1

− m

2

m

1

+ m

2

V

1

V

0

2

=

2 m

1

m

1

+ m

2

V

1

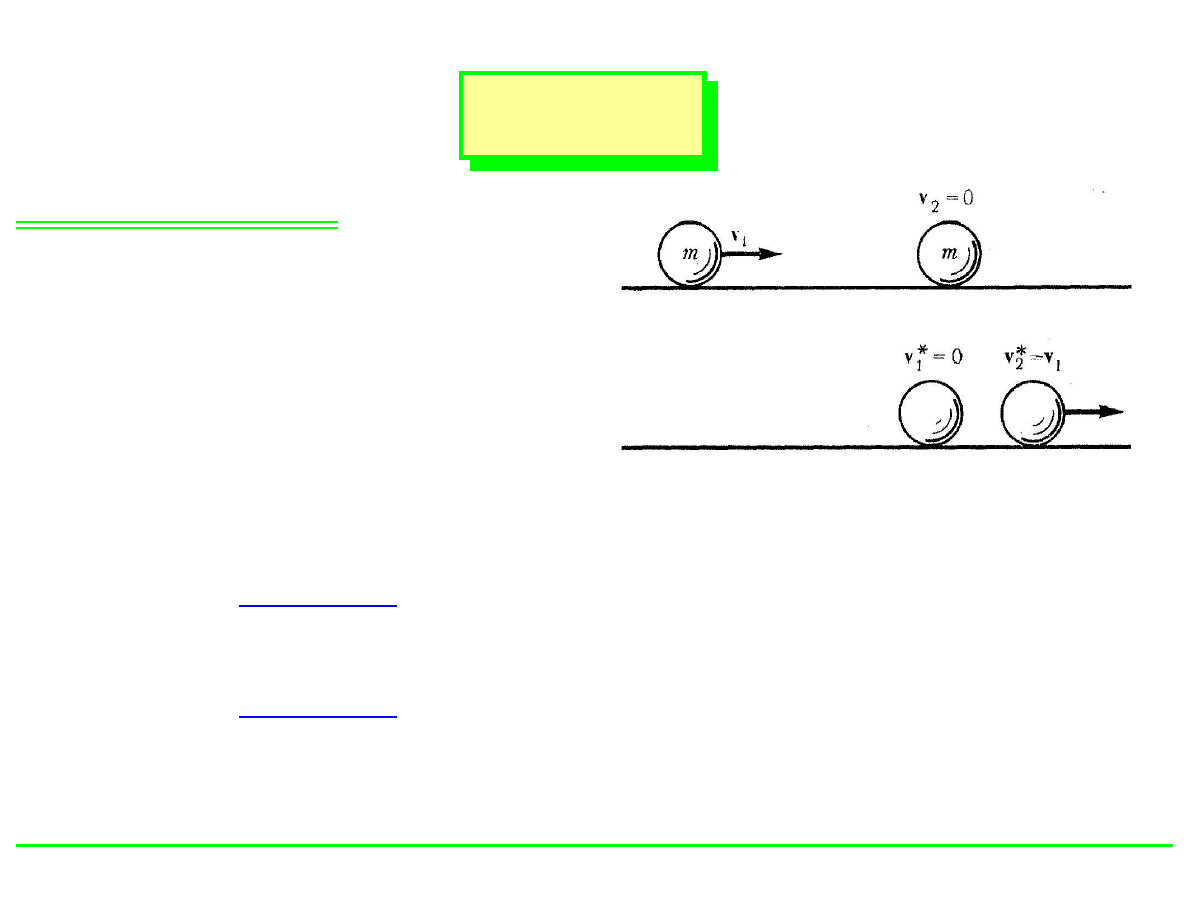
Przypadek szczególny:

m

1

= m

2

⇒

V

0

1

= V

2

= 0

V

0

2

= V

1

Zderzaj ˛

ace si˛e ciała “wymieniaj ˛

a si˛e” pr˛ed-

ko´sciami; rozwi ˛

azanie słuszne tak˙ze w przy-

padku

~

V

2

6= 0

A.F. ˙Zarnecki

Wykład XIV

13

Zderzenia

Zderzenia spr˛e˙zyste

m

1

> m

2

Masa

“pocisku”

wi˛eksza od masy

“tarczy”

:

Otrzymujemy:

V

0

2

> V

0

1

>

0

Przypadek graniczny:

m

1

m

2

⇒

V

0

1

=

m

1

− m

2

m

1

+ m

2

V

1

=

V

1

V

0

2

=

2 m

1

m

1

+ m

2

V

1

=

2 · V

1

“Pocisk” nie zauwa˙za zderzenia
“Tarcza” uzyskuje pr˛edko´s´c 2 · V

1

Po zderzeniu oba ciała poruszaj ˛

a si˛e w t ˛

a sam ˛

a stron˛e.

A.F. ˙Zarnecki

Wykład XIV

14

Zderzenia

Zderzenia spr˛e˙zyste

m

1

< m

2

Masa

“pocisku”

mniejsza od masy

“tarczy”

:

Otrzymujemy:

V

0

1

=

m

1

− m

2

m

1

+ m

2

V

1

<

0

V

0

2

=

2 m

1

m

1

+ m

2

V

1

>

0

Pr˛edko´s´c “pocisku” zmienia znak

⇒

“pocisk” odbija si˛e od “tarczy”

Przypadek graniczny:

m

1

m

2

⇒

V

0

1

= −V

1

V

0

2

= 0

Spr˛e˙zyste odbicie od
nieruchomej “´sciany”

A.F. ˙Zarnecki

Wykład XIV

15

Zderzenia

m

1

m

2

“Tarcza” oddala si˛e od “pocisku”

(“´sciana”)

“pocisk” traci energi˛e

“Tarcza” przybli˙za si˛e do “pocisku”

(“´sciana”)

“pocisk” zyskuje energi˛e

Mikroskopowy obraz ochładzania (ogrzewania) si˛e gazu przy rozpr˛e˙zaniu (spr˛e˙zaniu)

A.F. ˙Zarnecki

Wykład XIV

16

Zderzenia

Zderzenia nie centralne

Do tej pory rozpatrywali´smy tzw.

zderzenia centralne

,

dla których

parametr zderzenia b = 0

“pocisk” trafia w sam ´srodek “tarczy”

W przypadku gdy

b 6= 0

zderzenie trzeba rozpatrywa´c w dwóch wymiarach:

V

V

V’

V =0

2

1

2

1

Q

Q

1

2

b

x

y

Zasada zachowania p˛edu:

D

E

F

GH

I

F

H

J

K

L

D

I

F

H

G

p

x

:

m

2

V

0

2

cos θ

2

+ m

1

V

0

1

cos θ

1

= m

1

V

1

p

y

:

m

2

V

0

2

sin θ

2

− m

1

V

0

1

sin θ

1

= 0

Dla zderze´n sp˛e˙zystych:

E

k

:

m

1

V

02

1

2

+

m

2

V

02

2

2

=

m

1

V

2

1

2

Znajomo´s´c

m

1

, m

2

i V

1

(V

2

= 0

)

nie wystarcza do wyznaczenia

pełnej kinematyki zderzenia (

V

0

1

, V

0

2

, θ

1

i θ

2

) !

⇒

musimy ustali´c

b

albo jeden z parametrów rozproszenia

(np. k ˛

at θ

1

)

.

A.F. ˙Zarnecki

Wykład XIV

17

Zderzenia

Zderzenia nie centralne

Je´sli masy zderzaj ˛

acych si˛e spr˛e˙zyscie ciał s ˛

a równe

m

1

= m

2

⇒

zagadnienie bardzo si˛e upraszcza

V

1

V’

1

V

2

Q

2

Q

1

Q

2

Q

1

Z zasad zachowania:

~

V

0

1

+ ~

V

0

2

= ~

V

1

V

02

1

+ V

02

2

= V

2

1

⇒

wektory

~

V

1

,

~

V

0

1

i

~

V

0

2

tworz ˛

a trójk ˛

at prostok ˛

atny.

θ

1

+ θ

2

=

π

2

A.F. ˙Zarnecki

Wykład XIV

18

Zderzenia

m

1

= m

2

Fotografia zderzaj ˛

acych si˛e kul:

~

V

0

1

~

V

1

~

V

0

2

Zderzenie proton-proton w komorze p˛echerzykowej:

niska energia padaj ˛

acej wi ˛

azki

⇒

dynamika nierelatywistyczna

A.F. ˙Zarnecki

Wykład XIV

19

Zderzenia

m

1

= m

2

2

V’

V’

1

b=0

b=R

b=2R

b=0

b=R

b=2R

Stan ko´ncowy zale˙zy od parametru
zderzenia b

•

b

= 0

⇒

zderzenie centralne

~

V

0

2

= ~

V

1

~

V

0

1

= 0

•

b >

= 2R

⇒

brak zderzenia

(kule mijaj ˛

a si˛e)

~

V

0

2

= 0

~

V

0

1

= ~

V

1

A.F. ˙Zarnecki

Wykład XIV

20