Ćwiczenie Nr 320

Temat:

Pomiar pracy wyjścia termoelektronów

I. Literatura

1. Hannel J., Lampy elektronowe, WNT, W-wa 1968.

2. Ćwiczenia laboratoryjne z fizyki w politechnice, praca zbiorowa pod red.

T.Rewaja, PWN, W-wa 1978.

3. Pastusiak W., Elementy analizy błędu doświadczalnego, Inst.Fizyki PS, Szczecin 1982.

II. Metoda pomiarowa

Wartość pracy wyjścia termoelektronów należy wyznaczyć ze wzoru:



T

I 

kT T 

1

1

2ln

ln

1 2

−





T

I 

A =

2

2

T2 − T1

gdzie: I , I - wartości natężenia prądu nasycenia przy tym samym napięciu 1

2

anodowym oraz temperaturach żarzenia katody równych odpowiednio: T i T .

1

2

III. Przyrządy

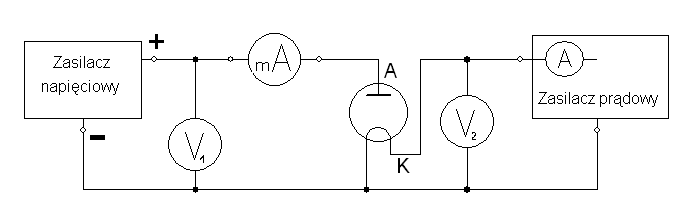
1. lampa (dioda z wolframowym włóknem żarzenia) - L, 2. zasilacz napięciowy DC POWER SUPPLY (0 ÷ 50 V) - Ua, 3. woltomierz (75 V) - V ,

1

4. miliamperomierz (7,5 mA),

5. zasilacz prądowy CURRENT SUPPLY (0 ÷ 3 A) - I , 2

6. woltomierz (7,5 V) - V ,

2

7. amperomierz (5 A).

IV. Wykonanie ćwiczenia:

1. Połączyć układ wg schematu

2. Ustawić wartość prądu żarzenia Iż=2, 90A i zanotować wartość napięcia żarzenia Uż.. Przy stałej wartości prądu żarzenia wykonać pomiar zależności prądu anodowego Ia od napięcia anodowego Ua. W tym celu wartość napięcia anodowego zmieniać co 5V notując wartość natężenia prądu Ia..

3. Pomiary opisane w punkcie 2 powtórzyć dla trzech innych prądów żarzenia Iż=2,75A; 2,80A; 2,85A.

4. Na wspólnym rysunku wykreślić cztery charakterystyki prądowo napięciowe lampy Ia=f(Ua) uzyskane przy różnych wartościach prądu żarzenia (tzn. dla różnych temperatur katody).

5. Wyznaczyć wartość prądu nasycenia In (wartości I1, I2, I3, I4) dla każdej charakterystyki. Przyjąć, że jest to wartość prądu Ia odpowiadająca maksymalnej wartości napięcia Ua.

6. Dla każdej charakterystyki obliczyć opór katody RT z równania Znając wartość oporu RT obliczyć temperaturę katody z równania T=T0+∆t

gdzie

T0= 273,15 K (temperatura zera 0C)

R0= 0,06 Ω ( rezystancja katody w temperaturze T0) α = 0,0046 K-1 ( współczynnik dla wolframu) 7. Dla każdej pary charakterystyk (prądów nasycenia I1-I2, I1-I3, I1-I4, I2-I3, I2-I4, I3-I4 i odpowiadających im par temperatur) obliczyć pracę wyjścia termoelektronów korzystając z zależności

Stałą Boltzmanna przyjąć: k=8,6167.10-5eV.K-1

8. Obliczyć średnią wartość pracy wyjścia i odchylenie standardowe średniej

9. Wyniki zebrać w tabelach:

Tab.1.

Iż= [A] Iż= [A] Iż= [A] Iż= [A]

Uż= [V] Uż= [V] Uż= [V] Uż= [V]

Lp.

Ua[V] Ia[mA] Ua[V]

Ia[mA]

Ua[V]

Ia[mA]

Ua[V]

Ia[mA]

1.

5

5

5

5

2.

10

10

10

10

3.

15

15

15

15

4.

20

20

20

20

5.

25

25

25

25

6.

30

30

30

30

7.

35

35

35

35

8.

40

40

40

40

9.

45

45

45

45

10.

50

50

50

50

Tab. 2.

Lp.

In [A]

RT [Ω]

∆t [K]

T [K]

1.

2.

3.

4.

Tab. 3.

A [eV]

A12

A13

2

A

∑( A − Aij )

14

A23

u( A)

i,

=

j

A

⋅

24

6 5

A34

Aij to odpowiednio A12 , A13, A14, A23, A24, A34 (6 liczb) u( A)