3.4.

Wyznaczanie metodą tensometrii oporowej modułu Younga i liczby Poissona

- 1/5 -

Politechnika Radomska

Instytut Mechaniki Stosowanej

Laboratorium

Wytrzymałości Materiałów

instrukcja do ćwiczenia

Wyznaczanie metodą tensometrii oporowej

modułu Younga i liczby Poissona

I ) C E L Ć W I C Z E N I A

Celem ćwiczenia jest wyznaczenie metodą tensometrii oporowej modułu

Younga E i liczby Poissona

ν

materiału belki poddanej czystemu zginaniu.

I I ) O B O W I Ą Z U J Ą C Y Z A K R E S W I A D O M O Ś C I

Definicja moduły Younga i liczby (współczynnika) Poissona, wykresy

momentów gnących i sił tnących dla belek statycznie wyznaczalnych, na-

prężenia w belkach, definicja czystego zginania; przeznaczenie, budowa

i zasada działania tensometru elektrooporowego, związek między względ-

ną zmianą rezystancji a odkształceniem tensometru, kompensacja tempera-

turowa.

I I I ) L I T E R A T U R A

1) Dziewiecki K., Misiak J.: Ćwiczenia laboratoryjne z wytrzymałości ma-

teriałów

, Wyd. WSI Radom 1996, ćwiczenie 3.4: „Wyznaczanie metodą

tensometrii oporowej modułu Younga E i liczby Poissona

ν

materiału zgi-

nanej belki”

2) Dziewiecki K., Misiak J.: Ćwiczenia laboratoryjne z wytrzymałości ma-

teriałów

, Wyd. WSI Radom 1996, p. 1.1: „Tensometria oporowa”

3.4.

Wyznaczanie metodą tensometrii oporowej modułu Younga i liczby Poissona

- 2/5 -

I V ) S T A N O W I S K O D O B A D A Ń

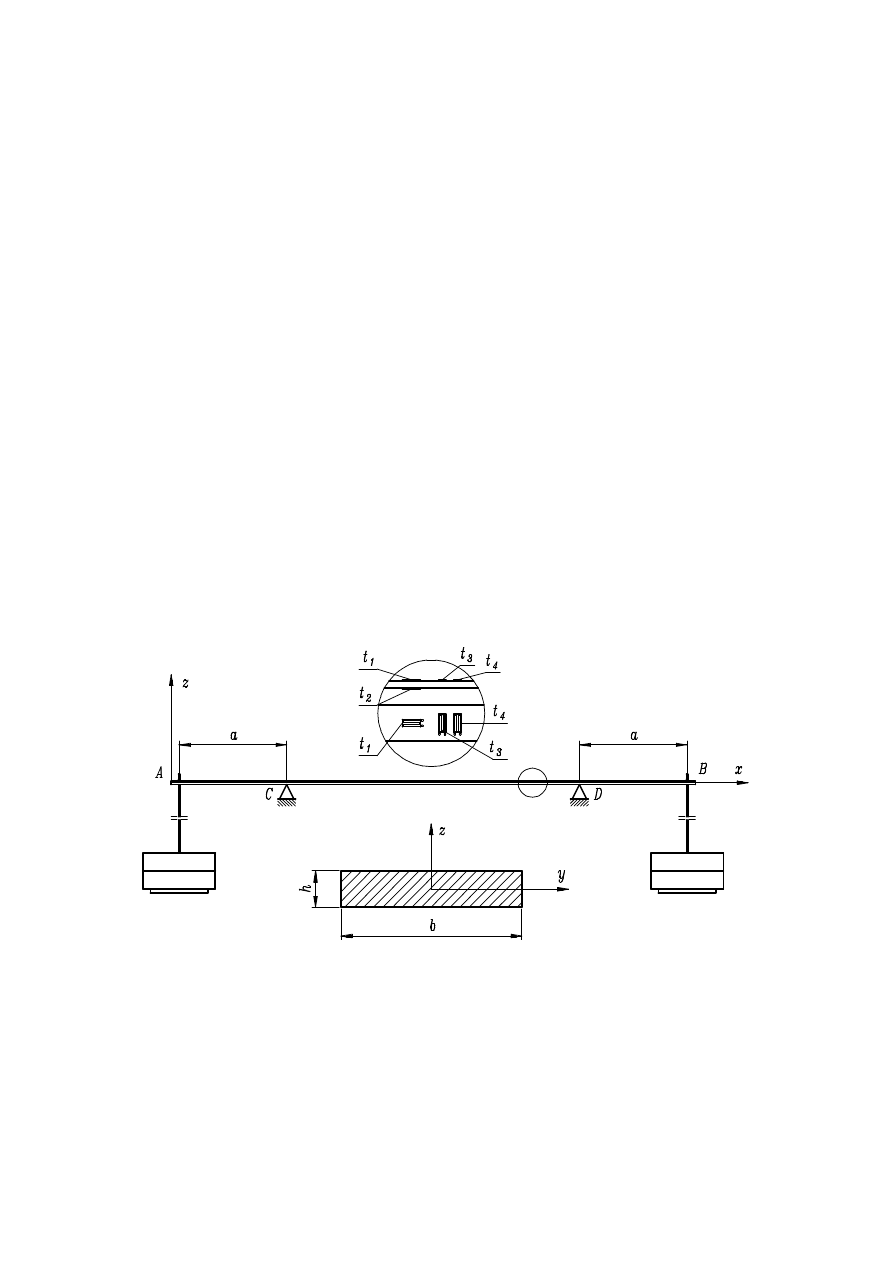
Schematyczny rysunek stanowiska pomiarowego przedstawia rys.1. Na

stalowej belce AB podpartej symetrycznie na podporach C i D naklejono

na odcinku między podporami na górnej powierzchni tensometry elektro-

oporowe: t

1

, t

3

i t

4

oraz tensometr t

2

na dolnej. Tensometry t

1

i t

2

naklejono

wzdłuż osi belki, natomiast tensometry t

3

i t

4

w kierunku poprzecznym.

Przy pokazanym sposobie obciążenia (szalki z równymi obciążnikami za-

wieszone na końcach) belka na odcinku między podporami znajduje się w

stanie czystego zginania. Tensometr t

1

jest rozciągany i mierzy odkształce-

nie

ε

w

w kierunku osi belki, natomiast pozostałe tensometry są ściskane:

tensometr t

2

mierzy odkształcenie -

ε

w

, zaś tensometry t

3

i t

4

odkształcenie

w kierunku poprzecznym

ε

p

=-

νε

w

. Tensometry są włączone do kanałów A i

B

wzmacniacza tensometrycznego TT6C. Sposób ich podłączenia, zapew-

niający równocześnie kompensację temperaturową, ilustruje rysunek 2.

Rys.1. Schemat stanowiska pomiarowego

Wymiary stanowiska: a=300

±1

mm, b=50

±0.1

mm, h=10.15

±0.05

mm.

Błąd względny wartości sił obciążających szalki

∆

P/P

=±0.5%.

3.4.

Wyznaczanie metodą tensometrii oporowej modułu Younga i liczby Poissona

- 3/5 -

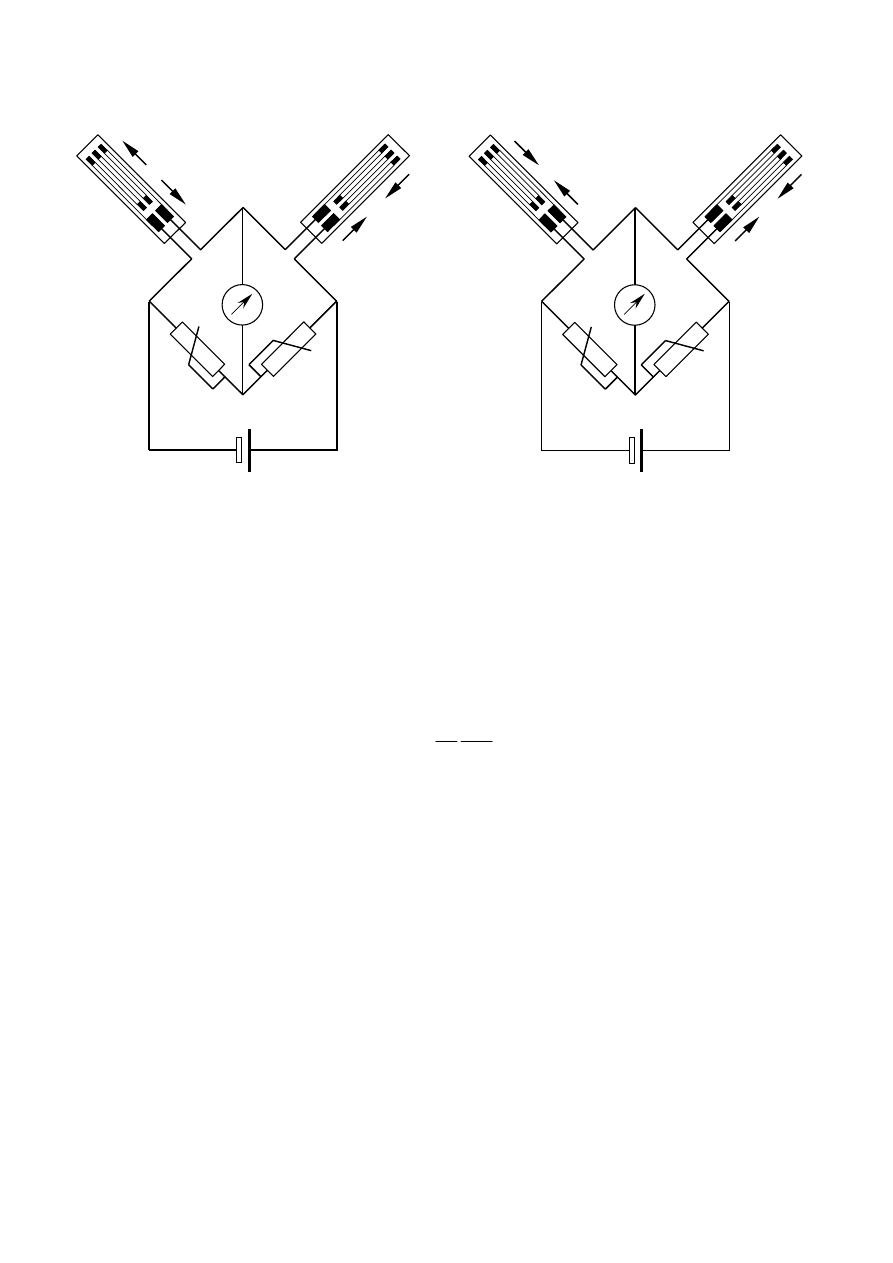
Rys.2. Sposób podłączenia tensometrów do kanałów wzmacniacza

Związek między wydłużeniem względnym tensometru

ε

a zmianą

jego rezystancji

∆

R

wywołaną wydłużeniem ma postać:

0

1

R

R

K

∆

ε

=

gdzie: R

0

– rezystancja tensometru nie odkształconego, K – stała tensome-

tru.

Rezystancja tensometru po jego odkształceniu równa jest

(

)

K

R

R

R

R

ε

∆

+

=

+

=

1

0

0

.

Po odkształceniu belki rezystancje poszczególnych tensometrów zmienią

się zatem i będą wynosiły

(

)

(

)

K

R

R

K

R

R

1

0

3

1

0

1

1

1

νε

ε

−

=

+

=

(

)

(

)

K

R

R

K

R

R

1

0

4

1

0

2

1

1

νε

ε

−

=

−

=

.

Napięcie panujące między punktami A i B mostka, a tym samym wychyle-

nie

α

wskazówki przyrządu, proporcjonalne jest do różnicy rezystancji są-

siednich gałęzi, w których wpięte są tensometry

ε

1

=

ε

w

t

1

t

3

ε

3

=-

ν⋅ε

1

α

A

t

2

ε

2

=-

ε

1

t

4

ε

4

=-

ν⋅ε

1

α

B

kanał A kanał B

U

0

U

0

A

B

A

B

3.4.

Wyznaczanie metodą tensometrii oporowej modułu Younga i liczby Poissona

- 4/5 -

(

)

(

)

(

)

(

)

ν

ε

α

ν

ε

α

+

−

=

−

=

+

=

−

=

1

1

0

1

4

2

0

1

3

1

KR

c

R

R

c

KR

c

R

R

c

B

A

.

Na podstawie powyższych zależności otrzymujemy wartość współczynnika

Poissona

B

A

B

A

α

α

α

α

ν

−

+

=

.

Wydłużenie względne w kierunku osiowym

ε

w

oblicza się z zależności

A

A

s

s

w

K

α

α

ε

ν

ε

ε













+

=

=

2

1

1

1

gdzie:

α

A

,

α

B

–

odczyty wskazań (działki) na kanałach A i B,

K=2.15±0.5% - stała użytych tensometrów,

ε

s

– zakres pomiarowy ustawiony dla kanału A,

α

s

=1 – przy odczycie wskazań na górnej części skali (

∆α

A

=

∆α

B

=0.05).

3.4.

Wyznaczanie metodą tensometrii oporowej modułu Younga i liczby Poissona

- 5/5 -

V ) P R Z E B I E G Ć W I C Z E N I A

1) Sprawdzić podłączenie tensometrów do wzmacniacza tensometryczne-

go.

2) Ustawić belkę symetrycznie na podporach i zawiesić szalki w równych

odległościach a=300mm od podpór.

3) Włączyć wzmacniacz tensometryczny i odczekać ok. 15 minut, po czym

dokonać odpowiednich regulacji kanałów A i B zgodnie z fabryczną in-

strukcją. Na obu kanałach ustawić zakres pomiarowy

ε

s

=0.3.

4) W razie potrzeby skorygować ustawienie zera.

5) Obciążyć szalki siłami P=100N. Zanotować w tabeli protokołu wartość

siły obciążającej szalkę.

6) Na obu kanałach odczytać wskazania

α

A

i

α

B

(na górnej części skali).

Odczytane wartości zanotować w tabeli protokółu.

7) Odciążyć belkę.

8) Powtórzyć czynności wymienione w p.4÷7. Liczbę powtórzeń ustalić z

prowadzącym ćwiczenie.

9) Wyłączyć wzmacniacz tensometryczny.

10) Wykonać sprawozdanie z ćwiczenia.