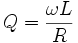
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
TERMIN 2 WRZENIEŃ 2006
SĄ TO ZADANIA Z UBIEGŁYCH EGZAMINÓW, JEŻELI DOSTRZEGACIE JAKIES BŁEDY PROSZĘ O
KONTAKT GG: 7266656. POZDRAWIAM :P
ZAD 1.
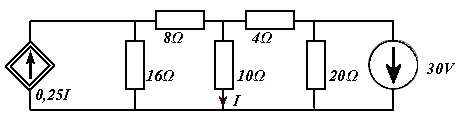
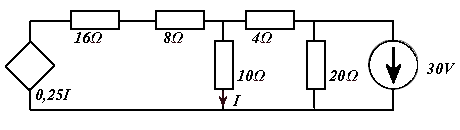
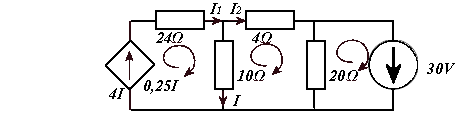
W oparciu o jedną z metod sieciowych(prądów oczkowych lub napięć węzłowych) napisać równania opisujące obwód o schemacie jak na rysunku, a następnie obliczyć prąd I płynący przez rezystor 10Ω oraz moc PE źródła napięciowego 30V.
I − I − I = 0
1
2
I = I − I
1
2
24 + 10
−10
0 I
4 I
1
− 10
10 + 4 + 20
− 20 I
=
2
0
0
− 20
20 I
30
3
34
−10
0 I
4 I
1
−10
34
− 20 I
=
2
0
0
− 20
20 I
30
3
34 I −10 I
= 4 I
I
I
I
I
1
2
34 −10 − 4( + ) = 0
1
2
1
2
−10 I + 34 I − 20 I = 0
÷ 2
⇒
I
I
I
1
2
3
− 5 +17
−10
= 0
1
2
3
− 20 I + 20 I = 30 ÷10
− 2 I + 2 I
=
3
2
3
2
3
1
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
3
0 I − 6 I
= 0
5
I + I
= 0
I = −5 I
1
2
1
2
2
1
− 5 I +17 I −10 I = 0 ⇒ − 5 I +17 I −10 I = 0
1
2
3
1
2
3
− 2 I + 2 I
= 3
− 2 I + 2 I
= 3
2
3
2
3
− 5 I −17 ⋅5 I −10 I = 0
− 90 I −10 I = 0 ÷10
× 2
1
1
3
1
3
⇒
1
0 I + 2 I
= 3
1
3
10 I + 2 I
= 3
1
3
−18 I − 2 I = 0
1
3
10 I + 2 I = 3
1
3
− 8 I
= 3
1
3
3 15
I = −
I = −5 − =
1
8
2
8
8
3
15
18
I = I − I = − −
= −
1
2
8
8
8
P = U ⋅ I
?
2
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
ZAD 2.
Podać podstawową definicje kondensatora. Uściślić tę definicje dla kondensatora liniowego:
a) stacjonarnego,
b) niestacjonarnego
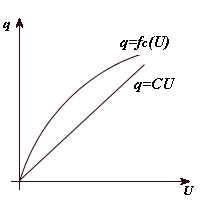
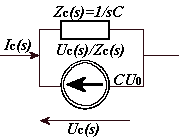
Napisać zależności i=f(u) dla obu typów kondensatora. Narysować przykładową charakterystykę kondensatora nieliniowego i zilustrować na niej pojęcia pojemności statycznej i pojemności różniczkowej(dynamicznej). Podać i objaśnić schemat zastępczy liniowego kondensatora stacjonarnego przy rachunku operatorowym (Laplace’a) oraz napisać związek między UC (s) a IC(s).
KONDENSATOR C – element elektryczny zbudowały z dwóch przewodników rozdzielonych dielektrykiem. Dwójnik, który spełnia(równanie) warunek: q = f ( u)
C
funkcja fC jest funkcją ciągła, rosnącą, różniczkowalną w przedziale (− ∞;+∞) , ponadto f = 0 (wykres leży w I i III ćwiartce układu współ. q, u i przechodzi C
przez środek układu współ.)
q f ( u)
POJEMNOŚĆ STATYCZNA:
C
C
= =
S / A
u u
u= u 0
dq df ( u)
POJEMNOŚĆ DYNAMICZNA:
C
C
=
=
R / A
du du u= u 0
q = C ⋅ u
KONDENSATOR LINIOWY:
C = C = C
R
S
STACJONARNY - kondensator, którego
charakterystyka jest linią prostą i jest nie zmienny w czasie.
ZALEŻNOŚĆ MIĘDZY PRĄDEM A NAPIĘCIEM DLA
KONDENSATORA:
dq
d
i =
⇒
i t
( ) =
{ f u t()
C [
]}
dt
dt
du t
( )
dla liniowego
i t
( ) = C
dt
t
1
u t
( ) =
∫ i τ() dτ
C −∞
-
inercyjny
-
bezstratny
-
gromadzący energię
3


















































OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
NIESTACJONARNY – zmienny w czasie.
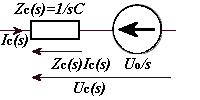
OPERATOROWE SCHEMATY ZASTĘCZE:
1 t
u ( t) =
i (τ ) dτ
u (0+
ic(t)
C
C
∫
+
)
C
C
C
0
[u
u
1
u
c(o+)=u]
c(t)
u ( s) =
I ( s
0
) +
C
sC C
s
I ( s) = sC ⋅ U ( s) − C ⋅ U
C
C
0
4
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
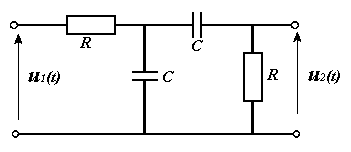
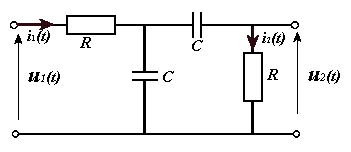
ZAD. 3
Zdefiniować pojęcia:
• transmitancja prądowo – napięciowa
układu
• odpowiedz impulsowa układu
• odpowiedz skokowa układu
Podać i omówić związki między nimi obliczyć i
narysować obydwie odpowiedzi obwodu o
schemacie pokazanym obok.
POJECIA Z ZAD. 5 TERMIN 1 CZERWIEC 2006
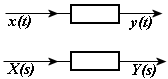
TRANSMITANCJA NAPIĘCIOWA UKŁADU – inaczej funkcja przenoszenia układu.
Stosunek transformaty Laplace’a odpowiedzi obwodu do transformaty Laplace’a wymuszenia przy zerowych warunkach początkowych.
Y ( s)
U ( s)
H ( s)
1
=
=
|| H(s) zapisywany
X ( s)
U ( s)
2
również jako TV
ODPOWIEDZ IMPULSOWA UKŁADU – odpowiedź układy na wymuszenie w postaci impulsu Diraca. Odpowiedz impulsowa jest określona jako transformata odwrotna transformaty Laplace’a transmitancji operatorowej.
impuls delta Diraca
0
dla
t ≠ 0
δ ( t) = ∞ dla t = 0
x( t) = δ ( t)
X ( s) = [
L x( t)] = [
L δ ( t)] = 1
Y ( s) = H ( s) ⋅ X ( s) = H ( s) ⋅1 = H ( s) y( t)
= h( t)
1
= L− [ H ( s)]
x( t )=δ ( t )
H ( s) = [
L h( t)]
h( t)
1
= L− [ H ( s)]
ODPOWIEDZ SKOKOWA UKŁADU – odpowiedz układu na wymuszenie w postaci skoku jednostkowego Heaviside’a
5
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
0 dla t < 0
1
t
(
1 ) =
dla
t = 0
2
1 dla t > 0
1
x t
( ) = t
(
1 )
X ( s) = L[ x t
( )] = L
t
(
1
[
)] = s
H ( s)
1 H ( s)
Y ( s) =
y t
( )
= r t
( ) = −
L
x( t )= (
1 t )
s
s
ZWIĄZEK MIĘDZY ODPOWIEDZIĄ IMPULSOWĄ A ODPOWIEDZIĄ JEDNOSTKOWĄ: d
h( t) =
[ r( t)]
dt
1
d
δ ( t) =
[ (
1 t)]
(
1 t) = ∫ δ ( t) dt
−∞
dt
1
1
C =
F
1
,
0
C =
C =
sC
s ⋅ 1
,
0
R =
Ω
5
,
2
L = Ls
U ( s)
H ( s)
1
=
n
U ( s)
2
U 1
U
1
1
2
H ( s)
+ RsC
1
=
=
⋅
=
?
n
U
2 + RsC U
2 + RsC
1
1
6
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
ZAD. 4
Zdefiniować następujące parametry sygnału okresowego:
• okres
• częstotliwość podstawowa
• wartość średnia
• wartość skuteczna.
Obliczyć tę parametry dla napięcia, które opisane jest wyrażeniem:
π
u( t) = 4 cos(2π ⋅12 ⋅103 t)+ 6cos 2π ⋅14 ⋅103 t +
{ t[ s]
[
u V ] }
3
// zwrócić uwagę na to czy średnia wartość nie wychodzi poza zakres//
Obliczyć tak że moc chwilowa i moc średnią wydzieloną przez ten sygnał na rezystorze o konduktancji G=0,1mS
POJECIA Z ZAD. 1 TERMIN 1 CZERWIEC 2006
SYGNAŁ OKRESOWY – to taki, który powtarza swe wartości co pewien czas.
∨
∧
[ x( t + T ) − x( t)] = 0
T
t ∈ (− ;
∞ +∞)
Najmniejsza z takich liczb T, dla których spełniona jest powyższa równość.
1
CZĘSTOŚĆ SYGNAŁU – liczba cykli w jednostce czasu f =
. Pulsacja
o
T
podstawowa ω = 2 f
π
o
o
WARTOŚĆ MIĘDZYSZCZYTOWA – to zakres zmienności wartości chwilowej sygnału. x
= [ x( t)]
− [ x( t)]
pp
max
min
WARTOŚĆ ŚREDNIA – wartość sygnału stałego równoważnego danemu sygnałowi zmiennemu, pod względem pola ograniczonego wykresem ilustrującym zmienność wartości chwilowej w czasie.
1
o
x
x t
( ) dt
o
∫ t + T
=
to
T
WARTOŚĆ SKUTECZNA – wartość sygnału stałego równoważnego danemu sygnałowi zmiennemu pod względem przenoszonej mocy średniej.
1
o
x
x 2 t
( ) dt
sk
∫ t + T
=
to
T
7
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
π
3
3
u t
( ) = 4 cos(2π ⋅12 ⋅10 t)+ 6 cos 2π ⋅14 ⋅10 t +
{ t[ s] u V
[ ] }
3
ω = 2π ⋅12 ⋅
3
10
0
2π
1
T =
=
−3
10
2π ⋅12 ⋅
3
10
12
1
f =
= 12 ⋅
3
10
T
1
t
T
−
+
3
10
1
π
3
3
3
o
x =
x t
( ) dt
12 10
4 cos 2π 12 10
6 cos 2π 14 10
0
∫
=
⋅
∫12
( ⋅ ⋅ t)+
⋅
⋅
t +
dt
T t
0
o
3
2
1 10−3
π
x
3
12
3
3
= 12 ⋅10
4 cos 2π ⋅12 ⋅10
+ 6 cos 2π ⋅14 ⋅10
∫
+
ś r
(
t )
t
dt
0
3
Moc chwilowa i moc średnia wydzielona przez ten sygnał ma rezystancje o konduktancji G=0,1mS
...??
8
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
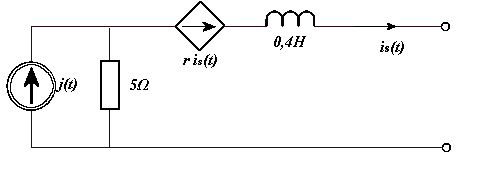
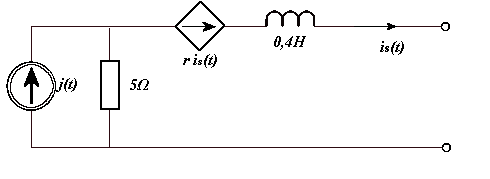
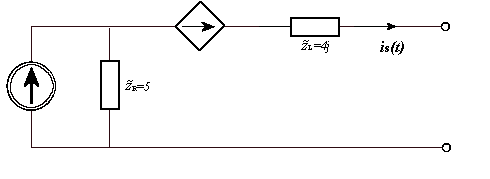
ZAD. 5
Zdefiniować pojęcia:
• moc dysponowana źródła
• dopasowanie energetyczne obciążenia do źródła
i wypunktować różnice w obydwu tych pojęciach dla: a) obwód prądu stałego
b) obwód prądu sinusoidalnego
Obliczyć z jakich elementów należy zbudować obciążenie źródła o podanym obok schemacie, aby na obciążeniu tym wydzielała się maksymalna moc. Obliczyć również wielkość tej mocy.
POJECIA Z ZAD. 4 TERMIN 1 CZERWIEC 2006
MOC DYSPONOWANA ŹRÓDŁA – to maksymalna moc, jaką z danego źródła można przekazać do obciążenia:
E 2
1 2
P
J R
.ź
=
=
dysp r
4 R
w
4
w
Moc wydzielana w obciążeniu jest zawsze mniejsza od mocy dysponowanej źródła, a tylko w przypadku, gdy obciążenie jest dopasowane energetycznie do źródła mocy wydzielana w nim jest równa mocy dysponowanej źródła: P
= ( P )
= P
max
.ź
L
L
dysp
R = R
L
W
DOPASOWANIE ENERGETYCZNE OBCIĄŻENIA DO ŹRÓDŁA – zapewnienie warunków pozwalających na przekazywanie maksymalnej mocy ze źródła do obciążenia.
//źródło sterowane, nie można bezpośrednio
wliczyć impedancji
π
j( t) = 60 cos10 t −
[
m ]
A
r = [
2 Ω]
4
~
Z = j L = j ⋅10 ⋅ 4 ⋅10 1
−
ω
= 4 j
L
9
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
ZAD. 6
Zdefiniować następujące parametry obwodu rezonansowego:
• częstotliwość rezonansowa f0
• dobroć Q
• rezystancja dynamiczna Rd
• trzy decybelowe pasmo przenoszenia(3dB)
Obliczyć te parametry dla obwodu będącego równoległym połączeniem trzech jednorodnych elementów R=50kΩ, L=40µH, C=40pF. Jak zmieniają się te parametry, gdy obwód pobudzany będzie z rzeczywistego źródła prądu harmonicznego o częstotliwości f0 i rezystancji wewnętrznej Rw=200kΩ
POJECIA Z ZAD. 7 TERMIN 1 CZERWIEC 2006
ω
1
CZĘSTOTLIWOŚĆ REZONANSOWA -
0
f =
gdzie ω =
o
π
2
0
LC
ω0 – pulsacja rezonansowa dwójnika – pulsacja dla której część urojona immitancji dwójnika jest równa zeru, a więc immitancja jest liczbą rzeczywistą.
DOBROĆ – stosunek maksymalnej wartości całkowitej energii zmagazynowanej w obwodzie do wartości całkowitej energii traconej w obwodzie w ciągu okresu odpowiadającego pulsacji rezonansowej obwodu ze współczynnikiem π
2 .
[ W ( t) + W ( t)
L
C
]
def. Q = 2
max
π ⋅
W ( t , t + T )
R
0
0
ω ω
= 0
Wzór pozwalający na obliczenie dobroci:
Dla cewki indukcyjnej o indukcyjności L dobroć wynosi: gdzie: ω - częstość wymuszonych zmian prądu,
R - oporność czynna cewki.
Dla kondensatora o pojemności C dobroć wyraża się wzorem: gdzie: ω - częstość wymuszonych zmian prądu,
R - zastępcza szeregowa oporność kondensatora.
W obwodzie zawierającym cewkę i kondensator:
L
C
ρ
Q =
=
R
R
Pulsacje graniczne wyznaczają TRZYDECYBELOWE PASMO PRZENOSZENIA obwodu: ω
B
o
= ω − ω =
3 dB
g
d
Q
10
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
~
1
REZYSTANCJA DYNAMICZNA - R ≅ Z
=
d
~
ω ω
= 0
Y ω ω
= 0
W praktyce:
2
R ≅ R ≅ R Q
d
L
L
L
Oporność dynamiczna informuje o wartości przyrostu prądu w elemencie przy określonej zmianie napięcia. Dla elementów liniowych takich jak rezystor jest ona stała i równa oporności statycznej, dla elementów nieliniowych jest ona zmienna, zależy od wartości prądu i napięcia stałego U
∆
określającego punkt pracy elementu. R =
d
I
∆
11
OBWODY I SYGNAŁY ZADANIA EGZAMINACYJNE
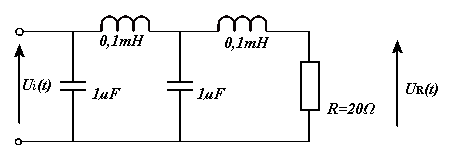
ZAD. 7
Do układu o schemacie jak na rysunku przyłożono napięcie
π
u (t) = 20 cos 1
05 t −
[
V ] . Obliczyć napięcie u
i
R(t) na rezystorze R, chwilową i
2
średnią moc wydzieloną na tym rezystorze pR(t) i PR oraz chwilową i średnią moc doprowadzoną do wejścia układu pi(t) i Pi.
/* Należy pamiętać, że przy zamianie na układ wskazowy zamieniamy również iS(t) na IS
Zwracać uwagę na źródła sterowane. */
12
Wyszukiwarka
Podobne podstrony:
egzamin 09 2010 pop B id 151733 Nieznany
Egzamin (5 09 2006)
Egzamin (5 09 2006)
Egzamin+14 09 2006
Egzamin wytrzymalosc 6 09 2006
Wyklad 09 2006
Egzamin zawodowy 2006 07
14,09,2006
egzamin08 09, egzamin08 09
Egzamin testowy 2006
Egzamin 3 09 2008 (Kubryński)
egzamin 09 2009 pop2
Mechanika egzaminy 2000 2006 (by Zboru)1[1] id 290871
09 2006
zadania egzaminacyjne zaoczne 2006 07 (PTM), elektro, 1, Podstawy Techniki Mikroprocesorowej
więcej podobnych podstron