Zadanie 1

Sygnał sinusoidalny oglądano na oscyloskopie cyfrowym. Zapisując w poniższej postaci uzyskano zamiast przebiegu sinusoidalnego sygnał bardzo zniekształcony.

% Zapis sygnału sinusidanego

fs=10

f=5

n=1:40;

y=sin(2*pi*(f/fs*n));

plot(n,y)

Jak poprawić ten zapis ,aby w oknie oscyloskopu zobaczyć dwa pełne okresu przebiegu sinusoidalnego?

Jaka jest częstotliwość analizowanego przebiegu?

Zadanie 2

Dany jest przebieg:

fs=20

f=5

n=0:1/fs: 2;

y=sin(2*pi*(f/fs)*n);

plot(n,y)

Ile okresów tego przebiegu widoczne będzie na ekranie?

Jak zmienić fs aby uzyskać pełen okres przebiegu? Jeśli fs jest częstotliwością próbkowania to zastosowana metoda jest dobrą?

Zadanie 3

Zapisz w Matlabie sygnał o częstotliwości 1 Hz próbkowany z częstotliwością 1000 Hz , tak aby w jednym oknie o szerokości 1s wartość maksymalna wypadała w 0.25 sek.

Zadanie 4

Dany jest zapis:

% Przebieg sinusoidalny

n = 0:1:10;

ts = 0.05;

y = sin(2*pi*10*n*ts);

stem(n*ts, y)

Jak poprawić ten plik aby widoczna była pełna sinusoida?

Ile najmniej punktów potrzeba umieścić na jednym cyklu sinusoidy aby pozostała ona niezniekształcona?

Zadanie 5

Napisać m-plik generujący ciągły i dyskretny sygnał sinusoidalny spełniający warunki: A – amplituda sygnału A = 5

f0 – częstotliwość przebiegu 1000Hz

fs – częstotliwość próbkowania fs = 2000 Hz φ0 – przesunięcie fazowe φ = π/4

tc – czas trwania przebiegu 6 ms.

Przedstawić sygnał w postaci sygnału ciągłego oraz w postaci sygnału dyskretnego tak aby w oknie graficznym można było oglądać dwa pełne jego okresy.

Zadanie 6

W programie MATLAB wygenerowano przebieg cosinusoidalny, a zapis m-pliku to:

% Generowanie dyskretnego przebiegu cosinusoidalnego dt = 0.01;

N = 0.3;

t = 0: dt : N

f0 = 300 % f0 częstotliwość w Hz

y = 9*cos(2*pi*f0*t* - pi/2)

stem (y)

Dlaczego nie oglądamy przebiegu sinusoidalnego? Jakie zmiany trzeba wprowadzić (nie zmieniając zapisu samego sygnału ) aby w oknie zobaczyć 1.5 okresu przebiegu sygnału?

Jeśli już uzyskaliśmy właściwy przebieg spróbuj jeszcze zmniejszyć częstotliwość f0 do 100Hz. Jaką część cosinusoidy obserwujemy?

Zadanie 7

Przeanalizuj wynik działania następującego pliku:

% Sinusoidy o różnych częstotliwościach

t = (1:100); f1 = 100;

f2 = 345; fs =245;

y1 = sin (2*pi*f1/fs*t);

y2 = sin (2*pi*f2/fs*t);

subplot (211);

plot (t/fs, y1);

ylabel ('amplituda (V)');

title ('sinusoida 100 Hz')

subplot (212);

plot (t/fs,y2);

ylabel('amplituda (V)');

title ('sinusoida 345 Hz');

Dlaczego takie uzyskaliśmy przebiegi? Czy jeśli przyjmiemy, że f2 =339Hz to uzyskamy już

różny od poprzedniego wynik?

Zadanie 8

Dany jest sygnał sinusoidalny x[n]=sin(5πn). Dla jakich wartości dyskretnego argumentu n+N sygnał x[n+M] spełnia warunek okresowości.

Zadanie 9

Dane są sygnały:

x[n]= 2sin[2n]

x[n]= 2cos[0.2πn]

Który z tych sygnałów jest okresowy? Jaki jest podstawowy okres tego sygnału?

Zadanie 10

Oblicz podstawowy okres sygnałów:

x[n]= 2sin[6πn]

x[n]= 2cos[6πn/15]

Jak zmieniłby się ten okres jeśli miałby on zapis np. x[n]= 2sin[2πn]?

Zadanie 11

Objaśnij następujący zapis:

A=1;

omega=2*pi/12;

phi=0;

n=-10:10;

y=A*cos(omega*n);

stem(n,y)

Ile pełnych okresów funkcji cos zobaczymy

Zadanie 12

Co zmieni się w odpowiedzi z zadania 11 jeśli zmienimy zapis na następujący: A=1;

omega=4*pi/12;

phi=0;

n=-10:10;

y=A*cos(omega*n)

stem(n,y)

Zadanie 13

Dane są sygnały:

U1=[zeros(1,250),ones(1,751)];

U2= [zeros(1, 751),ones(1,250)];

Jakie to są sygnały?

Co otrzymamy realizując polecenie U1-U2. Jak obejrzeć wynik tej operacji?

Zadanie 14

W Matlabie zapisano m-plik generujący sygnał sinusoidalny n=0:20;

Ts=0.0025;

t=n*Ts

f=sin(200*pi*t)

plot(t,f)

Jaka jest częstotliwość przebiegu? Czy jest on właściwie próbkowany?

Jaką liczbę okresów obserwujemy w oknie graficznym?

Zadanie 15

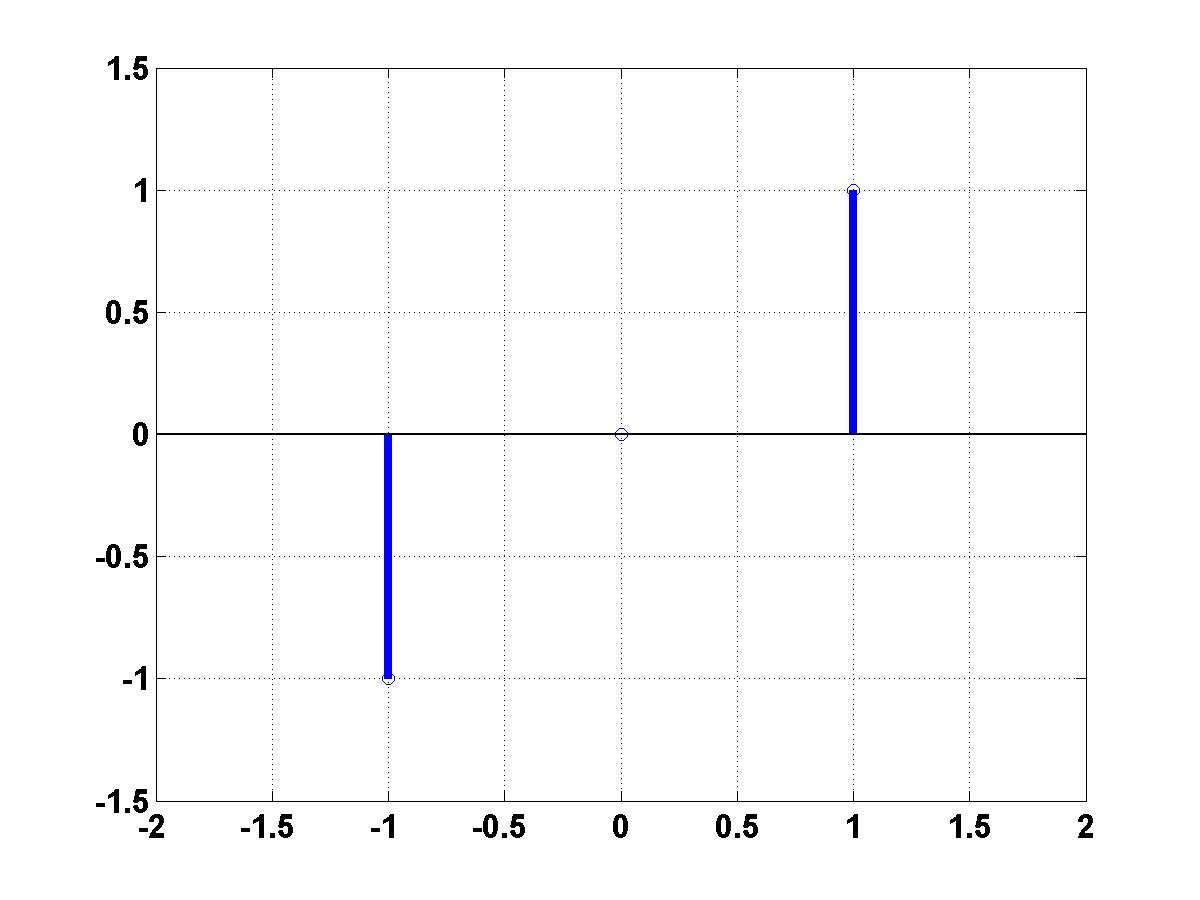
Na rysunku przedstawiono sygnał x1[n].

Narysuj sygnał:

a) y1 = x1[1 - n] ;

b) y1 = x1[ n-2];

y1 = x1[ n+2];

Zadanie 16

Jakie jest przesunięcie czasowe ( nie kątowe ) sygnału cos (80πt-0.4π) względem sygnału cos 80πt ?

Zadanie 17

Jakie jest przesunięcie czasowe sygnału cos(100π t − 0.2π ) względem

sygnału sin(100π t + π / 2) ?

Zadanie 18

Czy w wyniku sumowania poniższych sygnałów uzyskamy sygnał sinusoidalny czy niesinusoidalny? Wyjaśnij

zasadę.

2

2

x( t) = 2 *cos(2π * t + π / ) 3 − *cos 2

( π *3 t + π / )

3 + *cos(2π *5 t + π / )

3

3

5

2

2

x( t) = 2 *cos(2π * t + π / ) 3 − *cos(2π * 8 t + π / )

3 + *cos(2π * 27 t + π / )

3

3

5

Zapisz te sygnały w Matlabie.

Zadanie 19

W miejsce znaków zapytania wpisz odpowiedni zapis.

t=-4:0.01:4;

%przedział

(-4,4)

%z krokiem …….

(????)

x=2*t-1;

% x(t)=2t-1

y=2*(-t)-1;

% y(t)=x(???)

z=2*(-(t-3))-1;

%z(t)=y(???)=x(-(???))=x(?????)

Jeśli nie potrafisz obejrzyj wynik zapisując: plot(t,x,t,y,t,z)

Zadanie 20

Dany jest sygnał :

3 ⋅δ t = 0

5⋅δ t =

x( t) =

1



, gdzie δ jest impulsem Kroneckera

4 ⋅δ t = 2

1⋅δ t = 3

Narysuj sygnał y( t) = x( t − ) 2 ;

Zadanie 21

Ile prążków pojawia się w widmie idealnego sygnału sinusoidalnego?

Zadanie 22

Dane są sygnały jak na rysunku

5 4

5

3

4

3

1

1

t=0

t=1

t

t=0

t=1

t

t=2

t=2

t=4

t=3

t=3

t=5

Jakie operacje trzeba wykonać aby sygnał z prawej strony rysunku był równy sygnałowi z lewej strony?

Zadanie 23

Zapisz w Matlabie sygnał z zadania 22. Dokonaj jego przekształcenia w postaci y=x(1-2t). Narysuj ten sygnał.