1

MOSTKI POMIAROWE

Mostki prądu stałego

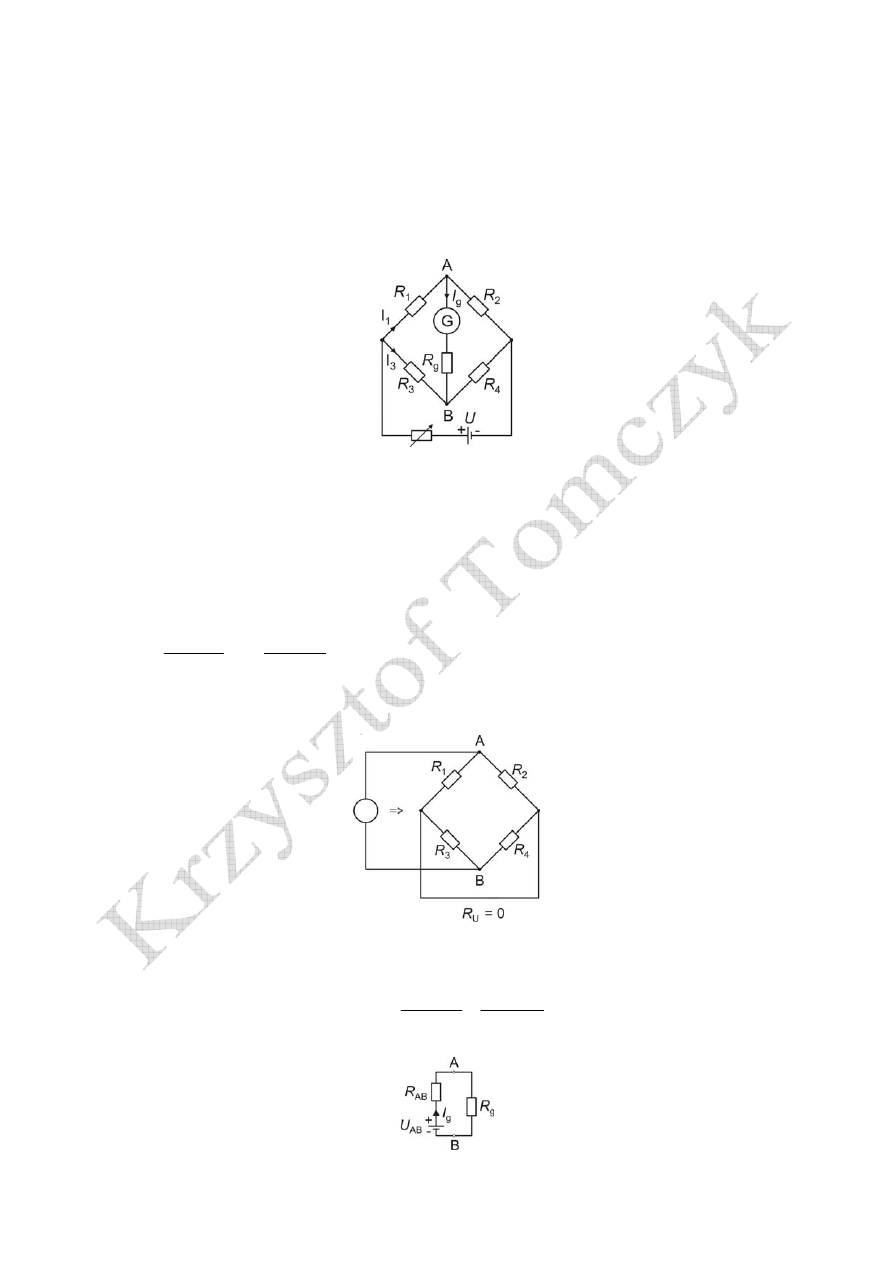
1. Mostek Wheatstone’a

Podstawowym zastosowaniem mostka Wheatstone’a jest pomiar rezystancji

1

R

włączonej we

wspólny układ z trzema opornikami

4

3

2

R

,

R

,

R

o znanych wartościach rezystancji.

Układ mostka Wheatstone’a

Warunki równowagi mostka -Metoda Thevenina

3

1

R

R

AB

U

U

U

−

=

3

3

1

1

R

I

R

I

U

AB

−

=

4

3

3

2

1

1

R

R

U

R

R

R

U

R

U

AB

+

−

+

=

Oporność wzierna

AB

R

- widziana od strony zacisków AB

Metoda Thevenina - wyznaczenie rezystancji widzianej od strony zacisków AB

4

3

4

3

2

1

2

1

R

R

R

R

R

R

R

R

R

AB

+

+

+

=

2

(

) (

)

(

)

[

]

4

3

4

3

2

1

4

3

2

1

3

2

4

1

4

3

4

3

2

1

2

1

4

3

3

2

1

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

U

R

R

R

R

R

R

R

R

R

R

R

U

R

R

R

U

R

R

R

U

I

g

g

g

AB

AB

g

+

+

+

+

+

−

=

+

+

+

+

+

−

+

=

+

=

W stanie równowagi

0

=

g

I

W celu spełnienia powyższego warunku musi zachodzić

0

3

2

4

1

=

−

R

R

R

R

Z powyższej zależności wyznacza się wartość szukanej rezystancji

2

4

3

1

R

R

R

R

=

Stan równowagi mostka można zatem osiągnąć dwoma sposobami:

- ustalając stosunek

4

3

R

R dokonuje się regulacji

2

R

(zastosowanie w bardzo dokładnych mostkach

laboratoryjnych)

- ustalając wartość

2

R

dokonuje się płynnej zmiany stosunku

4

3

R

R (zastosowanie w mostkach

technicznych)

Błąd względny graniczny

4

4

3

3

2

2

1

1

R

R

R

R

R

R

R

R

Δ

+

Δ

+

Δ

=

Δ

Uchyb nieczułości - określenie najmniejszego przyrostu

R

, który można zaobserwować na

wskaźniku zera

(

) (

)

(

)

[

]

4

3

4

3

2

1

4

3

2

1

3

2

4

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

U

I

g

g

+

+

+

+

+

−

=

Oznaczając

(

) (

)

(

)

[

]

4

3

4

3

2

1

4

3

2

1

R

R

R

R

R

R

R

R

R

R

R

M

g

+

+

+

+

+

=

mamy

2

3

2

4

1

4

1

M

)

R

R

R

R

(

'

M

MR

U

dR

dI

g

−

−

=

Ze względu na warunek

0

3

2

4

1

=

−

R

R

R

R

mamy

M

R

U

dR

dI

g

4

1

=

1

4

1

1

R

UR

M

dI

R

dR

g

=

- względny przyrost

1

R

3

g

I

dI

d

S

α

=

- czułość prądowa galwanometru

α

d

- najmniejsze widoczne wychylenie wskazówki galwanometru

I

g

S

d

dI

α

=

I

g

I

R

S

U

d

R

R

R

R

R

R

R

R

R

S

R

UR

M

d

R

dR

α

α

δ

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

+

+

+

+

=

=

=

3

4

2

1

4

3

2

1

1

4

1

1

1

2

Uchyb nieczułości jest odwrotnie proporcjonalny do czułości prądowej galwanometru oraz napięcia
zasilania. Można go zatem zmniejszyć stosując czulszy galwanometr lub, co jest łatwiejsze,
zwiększając napięcie zasilania.
Napięcie to jednak nie może być dowolnie duże, gdyż musi być ono dostosowane do dopuszczalnej
mocy oporników mostka, która nie przekracza 1W.

Przykład
Obliczyć uchyb nieczułości mostka Wheatstone’a o danych

V,

2

=

U

,

R

,

R

,

R

,

R

Ω

=

Ω

=

Ω

=

Ω

=

1000

10

1000

10

4

3

2

1

,

R

g

Ω

= 100

2

0

10

2

7

.

d

,

S

i

=

⋅

=

α

działki

%

.

.

.

R

3

5

7

1

10

1

6

10

1

6

10

2

2

2

0

10

1000

2

1000

10

100

1000

10

1000

10

−

−

⋅

=

⋅

=

⋅

⋅

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

+

+

+

+

+

+

=

δ

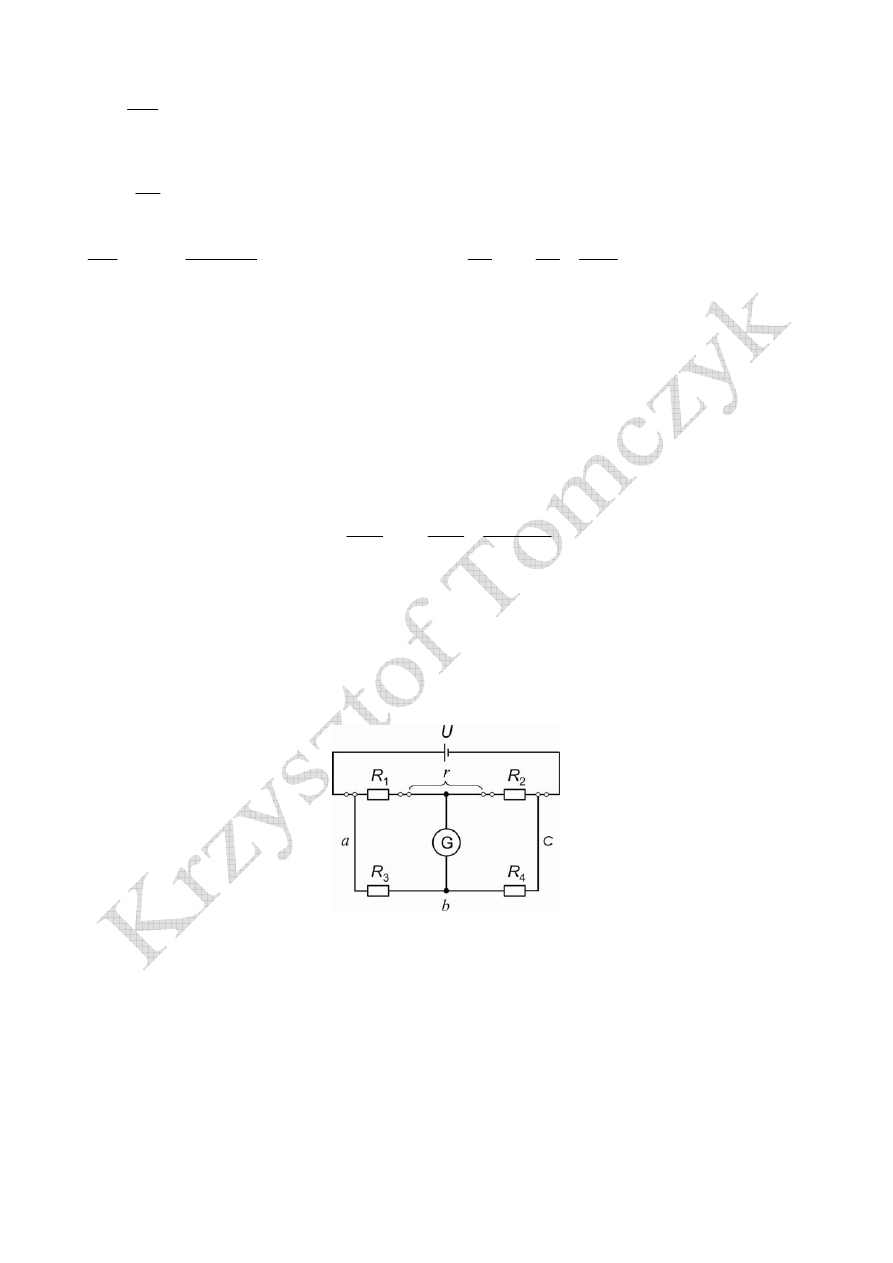
2. Mostek Thomsona
Mostek Thomsona stosowany jest do pomiaru małych rezystancji (0.0001-10

Ω ).

Stosując do pomiaru tak małych rezystancji mostek Wheatstone’a uzyskiwałoby się bardzo duże
błędy pomiaru, wnoszone przez rezystancję przewodów łączących oporniki.

Przewody łączące jako źródło błędu pomiaru małych rezystancji mostkiem Wheatstone’a

Rezystancje przewodów:

c

,

b

,

a

można zaniedbać, jeśli oporniki dekadowe

3

R i

4

R

mają dużą

rezystancję (rzędu setek lub tysięcy omów).

Istotny błąd wnosi natomiast rezystancja r , połączenia opornika mierzonego

1

R

o bardzo małej

rezystancji i opornika

2

R

(w praktycznych rozwiązaniach jest to opornik wzorcowy). Rezystancja

ta reprezentuje również rezystancję przejścia.
Opornik

2

R

również musi mieć małą rezystancję, zbliżoną do rezystancji

,

R

1

głównie dlatego żeby

czułość mostka była duża. Warunek równowagi można też uzyskać dla małego

3

R i dużego

,

R

2

jednak G musi być włączone pomiędzy mniej więcej podobnymi co do wartości rezystorami.

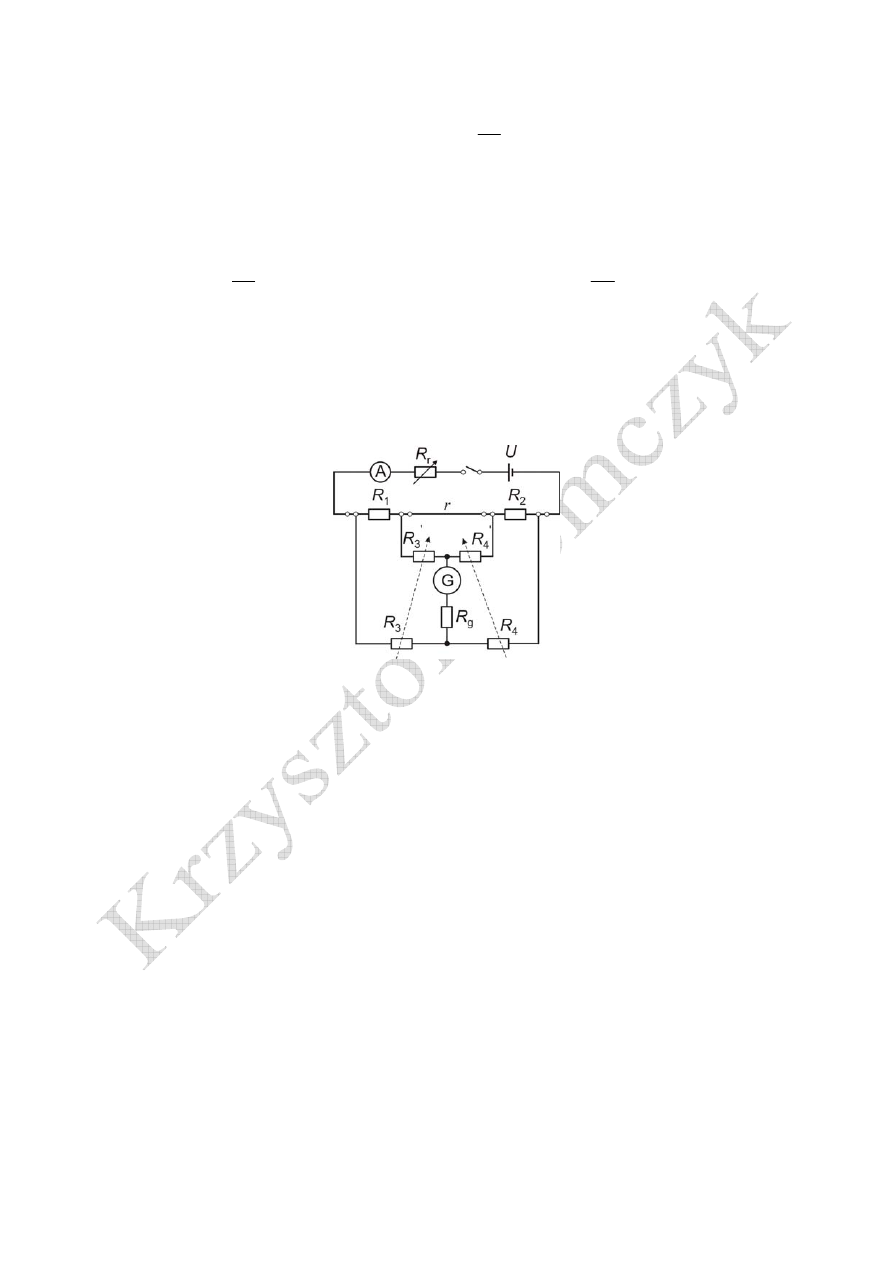
4

Rezystancja r może mieć wartość bliską a nawet większą od rezystancji

.

R

1

Proporcjonalność podziału rezystancji r do stosunku

4

3

R

R osiąga się poprzez równoległe dołączenie

do rezystancji r dwóch dekadowych oporników

'

R

3

i

,

R

'

4

pomiędzy które włącza się galwanometr

o rezystancji

.

R

g

Oporniki te mają wartości proporcjonalne lub równe dekadowym opornikom

3

R

i

4

R

oraz są z nimi sprzężone mechanicznie.

Zmiana stosunku

4

3

R

R powoduje taką samą zmianę stosunku

'

'

R

R

4

3

co odpowiada sytuacji

przesuwania punktu przyłączenia galwanometru wzdłuż rezystancji

.

r

Z uwagi na małe wartości rezystancji włączonych w górne ramiona mostka, konieczne jest
włączenie opornika regulującego prąd zasilania oraz kontrolującego ten prąd amperomierza.
Fabrycznie wykonany układ mostka Thomsona ogranicza się wyłącznie do dekad oporników i
zacisków. Opornik wzorcowy oraz układ zasilania dołącza do mostka użytkownik.

Układ mostka Thomsona

Mostki prądu zmiennego
W przeciwieństwie do mostków prądu stałego, liczba układów mostków prądu zmiennego jest
znacznie większa. Pomimo dużej różnorodności układów oraz szerokich zastosowań, wszystkie
mostki prądu zmiennego oparte są o układ mostka Wheatstone’a.
Bezpośredni wynik pomiarów przeprowadzanych za pomocą tych mostków stanowi pojemność i jej

δ

tg

R

+

bądź indukcyjność i jej

Q

R

+ oraz faza i częstotliwość.

Jako wskaźniki równowagi, w tego typu mostkach stosowane są najczęściej tzw. wskaźniki zera,
które realizowane są jako układy elektroniczne lub oscyloskopy w układem wzmacniacza na
wejściu.

5

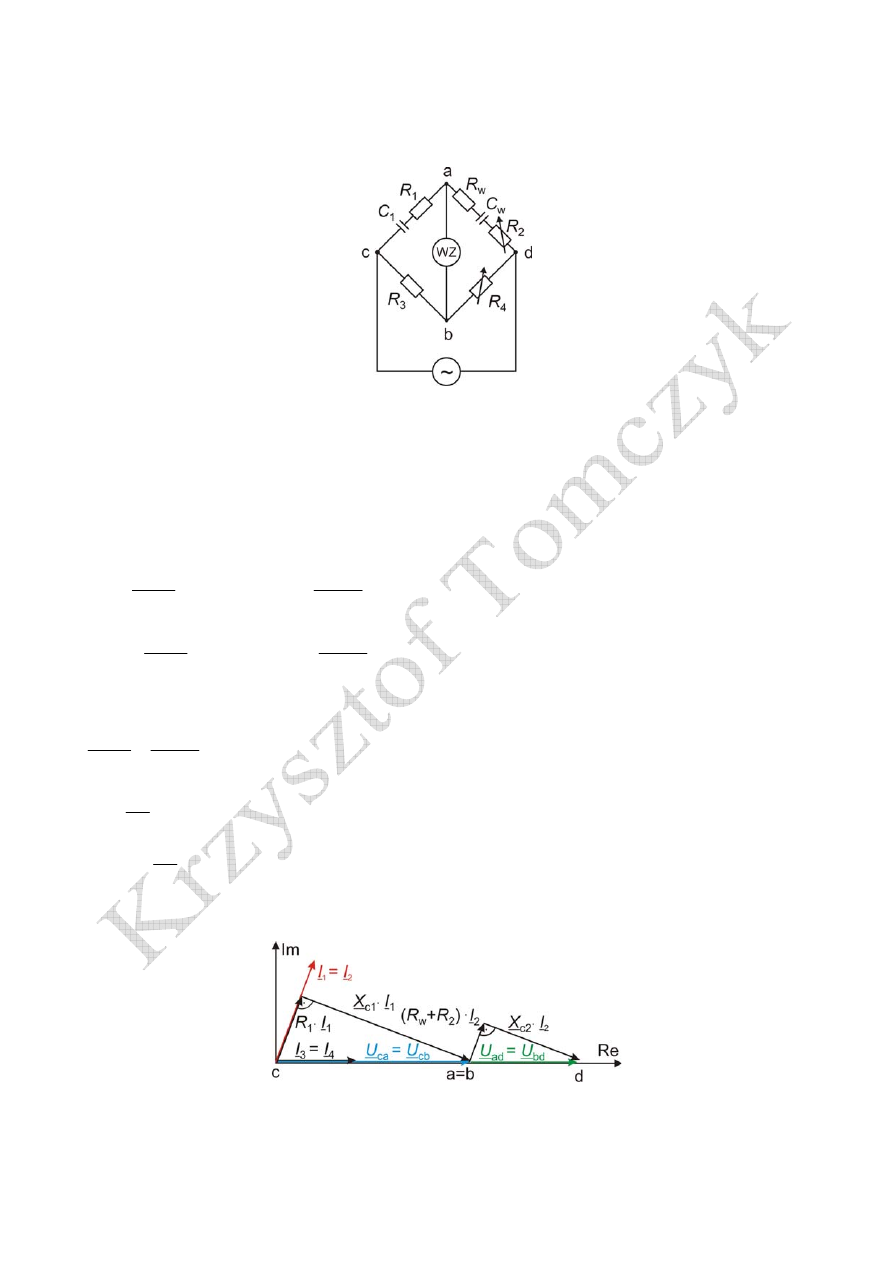
1. Mostek Wiena
Służy do pomiaru pojemności i kąta strat kondensatorów (w układzie szeregowym).

Układ mostka Wiena

1

1

R

,

C

- pojemność i rezystancja strat kondensatora badanego

w

w

R

,

C

- pojemność i rezystancja strat kondensatora wzorcowego

Warunki równowagi mostka

3

2

4

1

1

1

1

R

C

j

R

R

R

C

j

R

w

w

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

ω

ω

(

)

w

w

C

j

R

R

R

R

C

j

R

R

R

ω

ω

3

3

2

1

4

4

1

+

+

=

+

(

)

3

2

4

1

R

R

R

R

R

w

+

=

w

C

j

R

C

j

R

ω

ω

3

1

4

=

(

)

2

4

3

1

R

R

R

R

R

w

+

=

3

4

1

R

R

C

C

w

=

Wykres wskazowy zrównoważonego mostka Wiena

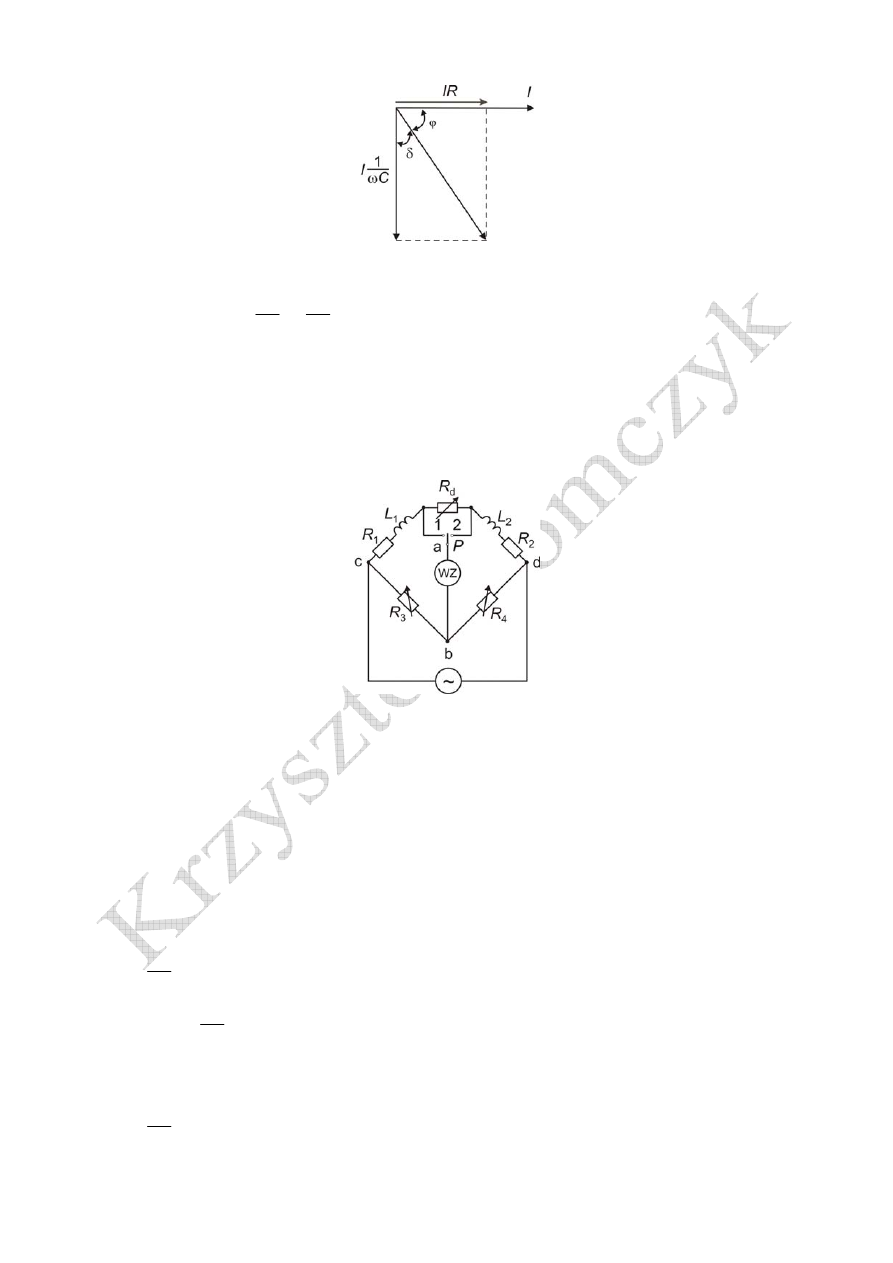
6

Kąt stratności kondensatora

2

2

4

3

2

3

4

2

1

1

1

R

C

R

R

R

R

R

C

R

C

tg

R

ω

ω

ω

δ

=

=

=

2. Mostek Maxwella

Służy do pomiaru indukcyjności cewek bez rdzenia ferromagnetycznego oraz ich rezystancji. Może
również służyć do pomiaru indukcyjności wzajemnej

.

M

12

Układ mostka Maxwella

Warunki równowagi
Dla przełącznika P w położeniu 1

(

)

(

)

3

2

2

4

1

1

R

L

j

R

R

R

L

j

R

d

ω

ω

+

+

=

+

(

)

3

2

3

2

4

1

4

1

R

L

j

R

R

R

R

L

j

R

R

d

ω

ω

+

+

=

+

(

)

3

2

4

1

R

R

R

R

R

d

+

=

3

2

4

1

R

L

j

R

L

j

ω

ω

=

4

3

2

1

R

R

L

L

=

(

)

4

3

2

1

R

R

R

R

R

d

+

=

Dla przełącznika w położeniu 2

4

3

2

1

R

R

L

L

=

7

d

R

R

R

R

R

−

=

4

3

2

1

Wielkością charakteryzującą jakość cewki indukcyjnej jest jej dobroć .

Q Dla szeregowego układu

zastępczego cewki wyznacza się ją ze wzoru

1

1

R

L

Q

ω

=

Wykres wskazowy zrównoważonego mostka Maxwella

3. Mostek Maxwella-Wiena

Służy do pomiaru indukcyjności własnej i rezystancji cewek powietrznych. Może również służyć
do pomiaru indukcyjności wzajemnej

.

M

12