

Kuźnia Talentów Informatycznych
Struktury danych i ich zas tos owania
Marcin Andrychowicz, Bole sław Kulbabiński, Toma s z Kulczyńs ki,
Jakub Łącki, Błażej Osiński, Wojciech Śmieta nka
prof. dr hab. Maciej M Sysło
Zes zyt dydaktyczny opracowa ny w ramach projektu edukacyjnego
— ponadregionalny program rozwija nia kompetencji
uczniów s zkół ponadgimna zjalnych w zakresie technologii
informacyjno-komunikacyjnych (ICT).
Wars zawska Wyższa Szkoła Informatyki
ul. Le wartows kiego 17, 00-169 Wars zawa
Projekt graficzny okładki: FRYCZ I WICHA
Warsza wa 2010
Copyright © Wars zawska Wyższa Szkoła Informatyki 2009
Publikacja nie jes t przeznaczona do sprzedaży.
< 4 >
Informatyka +
St r eszczenie
Celem kursu jest zapoznanie uczest nika z szeregiem różnych st rukt ur danych. P rezent owane jest
szerokie sp ekt rum zagadnień: od podst awowych st rukt ur wskaźnikowych jak st osy i kolejki, p oprzez
zbiory rozłączne, drzewa przedziałowe i wyszukiwań binarnych, aż do masek bit owych. P rzydat -
ność wymienionych st rukt ur danych ilust rują liczne przykłady zast osowań w algoryt mach opty-
malizacyjnych, grafowych czy t eż geomet rycznych, a t akże w rozwiązaniach zadań olimpijskich.
Uczest nik zapoznawany jest t akże pobieżnie z kont enerami z bibliot eki ST L, kt óre są prost ą w
użyciu implement acją niekt órych spośród omawianych st rukt ur.
Zakładana jest zna jomość jakiegoś języka programowania, na jlepiej C+ + , gdyż w nim napisane
są fragment y przykładowych programów. Zna jomość podst aw algoryt miki (wyniesiona choćby z
kursu „ P rzegląd podst awowych algoryt mów”) będzie dla uczest nika sporą pomocą.
Spi s t r eści
St r eszcze n ie
4
1
S t os
5
2
K ole jka
6
3
List a
7
4
K op ie c
9
4.1
Zast osowanie kopca w implement acji algoryt mu Dijkst ry . . . . . . . . . . . . . . . . . . . . . . .
12
5
D r ze w a r ozp in a ją c e
14
6
Zb ior y r ozł ą czn e
16
7
D r ze w a w y szu k iw a ń b in a r n y ch ( B ST )
19
7.1
Zrównoważone drzewa poszukiwań . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
8
D r ze w a p r ze d zia ł owe
24
8.1
Drzewo pot ęgowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
8.2
Drzewa przedziałowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
9
Te ch n ika za m ia t a n ia
32
9.1
Zamiat anie kąt owe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
9.2
Sort owanie kąt owe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
10 D r ze w a T R I E
36
11 A lgor y t m A h o-C or a sick
39
11.1 Algoryt m Bakera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
12 M a sk i b it ow e
41
12.1 P rogramowanie dynamiczne na maskach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
12.2 Meet in t he middle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
Lit e r a t u r a
45
> Struktury danych i ich za stosowania
< 5 >
1
St os
.
D e fi n icja 1. Stos t o st rukt ura danych, w kt órej dokładamy nowe element y na szczycie
st osu i zdejmujemy element y p ocząwszy od szczyt u st osu.
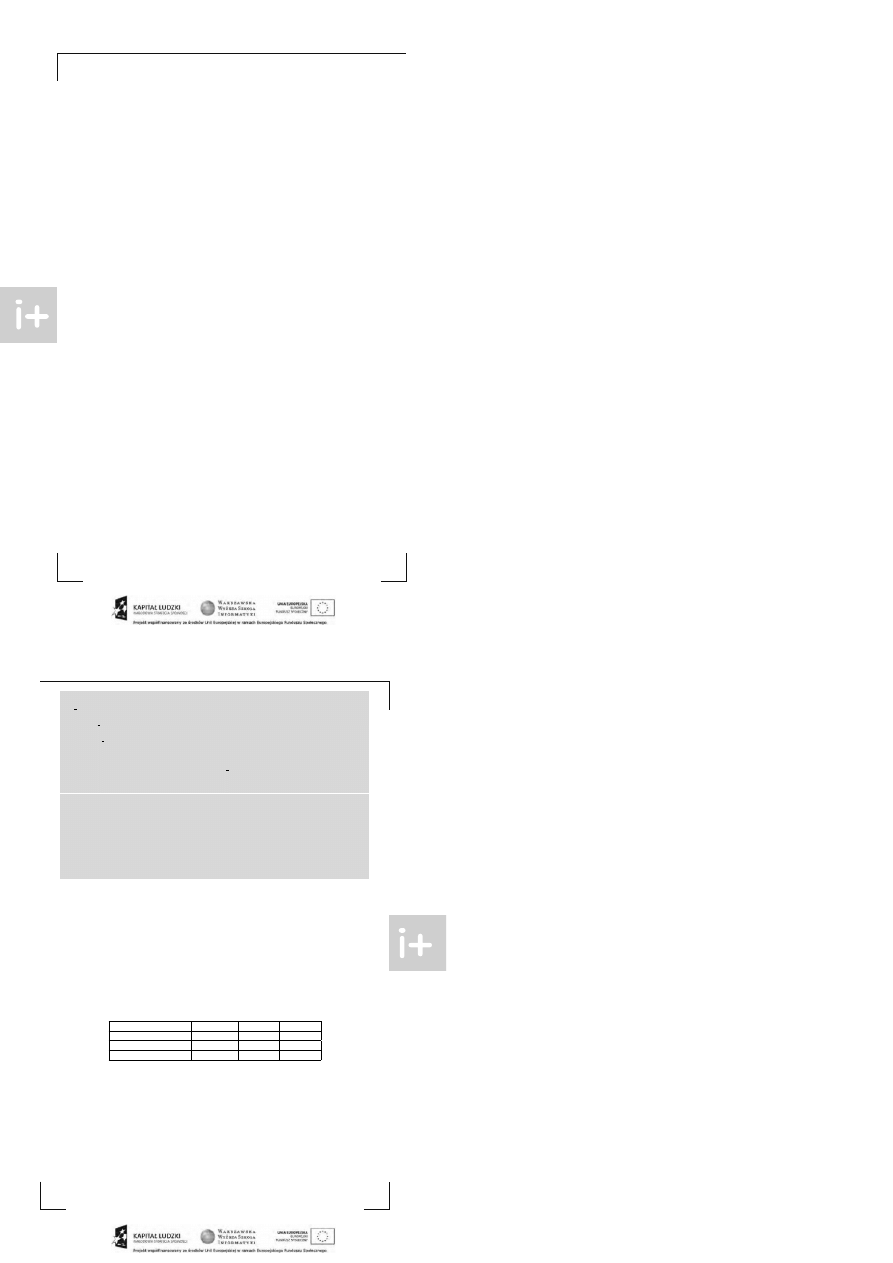
Będziemy chcieli, żeby st os w pamięci wyglądał jak nast ępuje:
st os
st os po zdjęciu element u ze szczyt u
st os p o dodaniu nowego element u
t op
15
10
42
t op
10
42
t op
17
10
42
P rzyjrzyjmy się t eraz implement acji st osu w języku C+ + za p omocą op erat orów new i del et e.
st r uct st ack_el ement {
/ / kl asa el ement st osu
i nt val ;
/ / war t ość w bi eżącym el emenci e
st ack_el ement * pr ev;
/ / wskaźni k na popr zedni el ement
st ack_el ement ( i nt _val , st ack_el ement * _pr ev) { / / konst r ukt or
val = _val ;
/ / ust awi amy war t ość
pr ev = _pr ev;
/ / ust awi amy wskaźni k na popr zedni
}
} ;
st r uct my_st ack {
st ack_el ement * _t op;
i nt _si ze;
my_st ack( ) {
/ / konst r ukt or
_t op = NULL;
/ / ust awi amy szczyt st osu na NULL
_si ze = 0;
/ / r ozmi ar na 0
}
voi d push( i nt a) {
/ / dodawani e el ement u do st osu
_t op = new st ack_el ement ( a, _t op) ; / / t wor zymy nowy el ement , kt ór ego
/ / popr zedni ki em będzi e _t op st osu
++_si ze;
/ / zwi ększamy r ozmi ar
}
voi d pop( ) {
/ / usuwani e el ement u ze st osu
st ack_el ement * t mp = _t op; / / w zmi ennej pomocni czej pami ęt amy szczyt
_t op = t mp- >pr ev;
/ / obni żamy szczyt
del et e t mp;
/ / usuwamy st ar y szczyt
- - _si ze;
/ / zmni ej szamy r ozmi ar
}
} ;

< 6 >
Informatyka +
Ć w iczen ie 1. Zaimplement uj dodat kowe met ody:
•
f r ont — zwraca jącą pierwszy element ze st osu
•
si ze — zwraca jącą liczbę element ów na st osie
•
empt y — zwraca jącą wart ość logiczną, czy st os jest pusty
Ć w iczen ie 2. Uzasadnij, dlaczego st os jest odpowiedni do implement acji przeszukiwa-
nia met odą DFS, ale nie nada je się do implement acji przeszukiwania met odą BFS.
Ć w iczen ie 3. P rzet est uj na komput erze działanie procedury pop, gdy wywołuje się ją
na pustym st osie.
Ć w iczen ie 4. Za pomocą kont enera st ack z bibliot eki ST L zaimplement uj przeszuki-
wanie grafu met odą DF S.
2
K ol ej ka
.
D e fin icja 2 . Kolej ka t o st rukt ura danych, w kt órej dokładamy elementy na koniec
i p obieramy elementy z przodu kolejki. W realnym świecie wyst ępuje jako kolejka w
sklepie: na jpierw obsługiwany jest klient z przodu kolejki, zaś nowi klienci ust awia ją się
na samym końcu kolejki.
W pamięci komput era chcielibyśmy reprezent ować kolejkę w t aki sposób:
head
17
10
42
t ail
P rzyjrzyjmy się t eraz implement acji kolejki w języku C+ + za pomocą op erat orów new
i del et e.
st r uct queue_el ement {
/ / el ement kol ej ki
i nt val ;
queue_el ement * next ;
queue_el ement ( i nt _val , queue_el ement * _next ) { / / konst r ukt or
val = _val ;
next = _next ;
}
} ;
st r uct my_queue {
queue_el ement * head, * t ai l ;
/ / gł owa i ogon kol ej ki
i nt _si ze;
my_queue( ) {
head = t ai l = NULL;
_si ze = 0;
}
voi d push( i nt a) {
/ / dodawani e el ement u na koni ec
++_si ze;
/ / zwi ększamy r ozmi ar kol ej ki
i f ( head == NULL) {
/ / j eśl i kol ej ka j est pust a
head = new queue_el ement ( a, NULL) ; / / ust awi eni e war t ości gł owy
t ai l = head;
/ / ust awi eni e war t ości ogona
}
el se {
/ / j eśl i kol ej ka ma
/ / j uż j aki eś el ement y
> Struktury danych i ich za stosowania
< 7 >
t ai l - >next = new queue_el ement ( a, NULL) ; / / nast ępni k ogona,
/ / t o nowy el ement
t ai l = t ai l - >next ;
/ / pr zechodzi my
/ / do ost at ni ego el ement u
}
}
} ;
Idea działanie t ego kodu jest prost a: cały czas t rzymamy wskaźniki na głowę i ogon kolejki.
Każdy element z kolejki ma wskaźnika na swojego nast ępnika. W yjmujemy element y wskazywane
przez głowę. Doda jemy element y na koniec, zaraz za ogonem.
Ć w iczen ie 5. Uzupełnij st rukt urę kolejki o nast ępujące met ody:
•
f r ont — zwraca jącą pierwszy element z kolejki
•
si ze — zwraca jącą liczb ę element ów w kolejce
•
empt y — zwraca jącą wart ość logiczną, czy kolejka jest pust a
•
pop — zdejmująca pierwszy element z przodu kolejki, wart o t ut a j poszukać podo-
bieńst w z pop ze st osu
Ć w iczen ie 6. Uzasadnij, dlaczego kolejka jest odp owiednią st rukt urą do przeszukiwania
met odą BF S, a nie nada je się do przeszukiwania met odą DF S.
Ć w iczen ie 7. Zaimplement uj przeszukiwanie grafu met odą BF S korzyst a jąc z kont e-
nera queue z bibliot eki ST L.
3
L i st a
List a dwukierunkowa t o st rukt ura danych, w kt órej każdy element ma swojego nast ępnika i po-
przednika.
head
17
10
42
t ail
Taka list a umożliwia wst awianie i usuwanie element ów z dowolnego miejsca. Spróbujmy napisać
szkielet st rukt ury danych list a. Zacznijmy od pojedynczego element u listy:
st r uct l i st _el ement {
/ / el ement l i st y
i nt val ;
l i st _el ement * pr ev, * next ;
l i st _el ement ( i nt _val , l i st _el ement * _pr ev, l i st _el ement * _next ) {
/ / konst r ukt or , ust awi a war t ości począt kowe
val = _val ;
/ / war t ość el ement u
pr ev = _pr ev;
/ / popr zedni k
next = _next ;
/ / nast ępni k
}
} ;
J ak widać, pot rzebujemy wskaźniki na poprzedni i nast ępny element listy. P oza t ym mamy pole
val , w kt órym jest przechowywana wart ość element u. P ojedynczy element st rukt ury my l i st ma
dwa wskaźniki, head i t ai l wskazujące na pierwszy i ost at ni element list y. P ośrednie element y są
p ołączone ze sobą.
st r uct my_l i st {
l i st _el ement * head, * t ai l ;
/ / wskaźni ki na gł owę i ogon l i st y
< 8 >
Informatyka +
i nt _si ze;
/ / r ozmi ar
my_l i st ( ) {
/ / konst r ukt or
head = t ai l = NULL;
/ / począt kowo gł owa = ogon = ni c
_si ze = 0;
}
voi d push_back( i nt a) {
/ / dodani e el ement u na koni ec
++_si ze;
i f ( head == NULL) {
/ / j eśl i kol ej ka j est pust a
head = t ai l = new l i st _el ement ( a, NULL, NULL) ;
}
el se {
/ / kol ej ka ma j uż j aki eś el ement y
t ai l - >next = new l i st _el ement ( a, t ai l , NULL) ;
t ai l - >next - >pr ev = t ai l ;
t ai l = t ai l - >next ;
}
}
voi d pop_back( ) {
/ / usuni ęci e el ement u z końca kol ej ki
- - _si ze;
l i st _el ement * t mp = t ai l ;
/ / zapami ęt uj emy st ar y ogon
/ / w zmi ennej t ymczasowej
t ai l = t ai l - >pr ev;
/ / popr awi eni e ogona
t ai l - >next = NULL;
/ / popr awi eni e nast ępni ka ogona
del et e t mp;
/ / usuni ęci e st ar ego ogona
}
l i st _el ement * sear ch( i nt x) {
/ / znal ezi eni e pi er wszego el ement u
/ /
o podanym kl uczu
l i st _el ement * e = head;
whi l e ( e ! = NULL) {
/ / i dzi emy po l i ści e aż znaj dzi emy
i f ( e- >val == x) r et ur n e;
/ / Hur r a! Znal eźl i śmy!
e = e- >next ;
/ / pr zechodzi my dal ej
}
r et ur n NULL;
/ / ni e znal eźl i śmy
}
voi d r emove( l i st _el ement * pt r ) {
/ / usuwani e el ement u
- - _si ze;
i f ( pt r - >pr ev == NULL) head = pt r - >next ;
/ / j eśl i ni e ma popr zedni ka
el se pt r - >pr ev- >next = pt r - >next ;
/ / j eśl i j est
i f ( pt r - >next == NULL) t ai l = pt r - >pr ev;
/ / j eśl i ni e ma nast ępni ka
el se pt r - >next - >pr ev = pt r - >pr ev;
/ / j eśl i on j est
del et e pt r ;
/ / usuni ęci e wskaźni ka
}
voi d wr i t e( ) {
/ / wypi sani e el ement ów l i st y
l i st _el ement * e = head;
whi l e ( e ! = NULL) {
cout <<e- >val <<" " ;
e = e- >next ;
}
cout <<endl ;
}
} ;
Obserwując t en kod należy zwrócić uwagę, że nie wszyst kie met ody wykonywane są w czasie
st ałym. Met oda sear ch działa w czasie liniowym ze względu na rozmiar list y.
> Struktury danych i ich za stosowania
< 9 >
Ć w iczen ie 8. J ako ćwiczenie wart o zaimplement ować dodat kowe met ody w st rukt urze
my l i st . Np.:
•
pop f r ont — usunięcie element u z przodu listy
•
push f r ont — dodanie element u z przodu listy
•
i nser t — dodanie element u do listy za wskazanym element em
Ć w iczen ie 9. Spróbuj przerobić st rukt urę my queue, żeby działała jak list a jednokie-
runkowa. W t ym celu należy dodać funkcjonalności: wyszukiwanie element ów, usuwanie
element ów ze środka, wst awianie element ów w środek list y.
Ć w iczen ie 10. Korzyst a jąc z list y dwukierunkowej zaimplement uj st rukt urę pozwala-
jącą na edycję t ekst u. W edycji t ekst u dozwolone są nast ępujące op eracje:
•
napisanie jednej lit ery zaraz za kursorem
•
usunięcie jednej lit ery z miejsca bezpośrednio za kursorem
•
przesunięcie kursora o jedno pole w lewo/ prawo
•
wypisanie całego t ekst u na ekran
Podsum owani e st r uk t ur
Wart o uważnie prześledzić działanie tych t rzech st rukt ur danych. Szczęśliwie są one wszyst kie
zaimplement owane w bibliot ece st andardowej C+ + ST L. Są t o odpowiednio kont enery st ack,
queue, l i st . Aut orzy tego dokument u st arali się zachować oryginalne nazwy met od t ak, aby
przesiadka na kont enery z bibliot eki ST L była możliwie bezbolesna. Drobne różnice są jedynie w
implement acji list y.
4
K opi ec
W st ęp
Kolejny fragment jest p oświęcony st rukt urze danych, zwanej kop ce m . W p oniższej t abeli p orów-
nano złożoności operacji na kopcu oraz t ablicy (nie-)posort owanej.
wst awienie
usunięcie
minimum
t ablica
O(1)
O(1)
O(n)
posort owana t ablica
O(n)
O(n)
O(1)
kopiec
O(log n)
O(log n)
O(log n)
Oznaczenia:
•
w st a w ie n ie — wst awienie element u
•
u su n ię cie — usunięcie element u na podanej p ozycji (a nie o danej wart ości)
•
m in im u m — znalezienie minimum
I m pl ement acj a p eł nego dr zewa binar nego
.

< 10 >
Informatyka +
D e fi n icj a 3. P e ł n e d r ze w o b in a r n e t o drzewo, kt órego wierzchołki ma ją co na jwyżej
dwóch synów (binarne) a liście
a
zna jdują się tylko na 2 poziomach, przy czym t e na
niższym poziomie są „z jednej st rony” (pat rz rys. 7.1).
1
2
3
4
5
6
7
8
9
10
11
12
Rys. 1: Numeracja wierzchoł ków peł nego drzewa binar nego
a
liś ć — wier zchoł ek nie posiadaj ący synów
W ierzchołki pełnego drzewa binarnego możemy p onumerować t ak, jak t o zost ało przedst awione
na rys. 7.1. Taka numeracja jest wygodna, gdyż:
•
lewy syn x t o 2x
•
prawy syn x t o 2x + 1
•
ojciec x t o x/ 2
W wierzchołkach p ełnego drzewa binarnego będziemy przechowywali pewne wart ości (np. liczby).
Drzewo binarne będziemy reprezent owali w p ost aci t ablicy heap, przy czym heap[ i ] oznacza
wart ość w i -t ym wierzchołku.
W ł asność kop ca
.
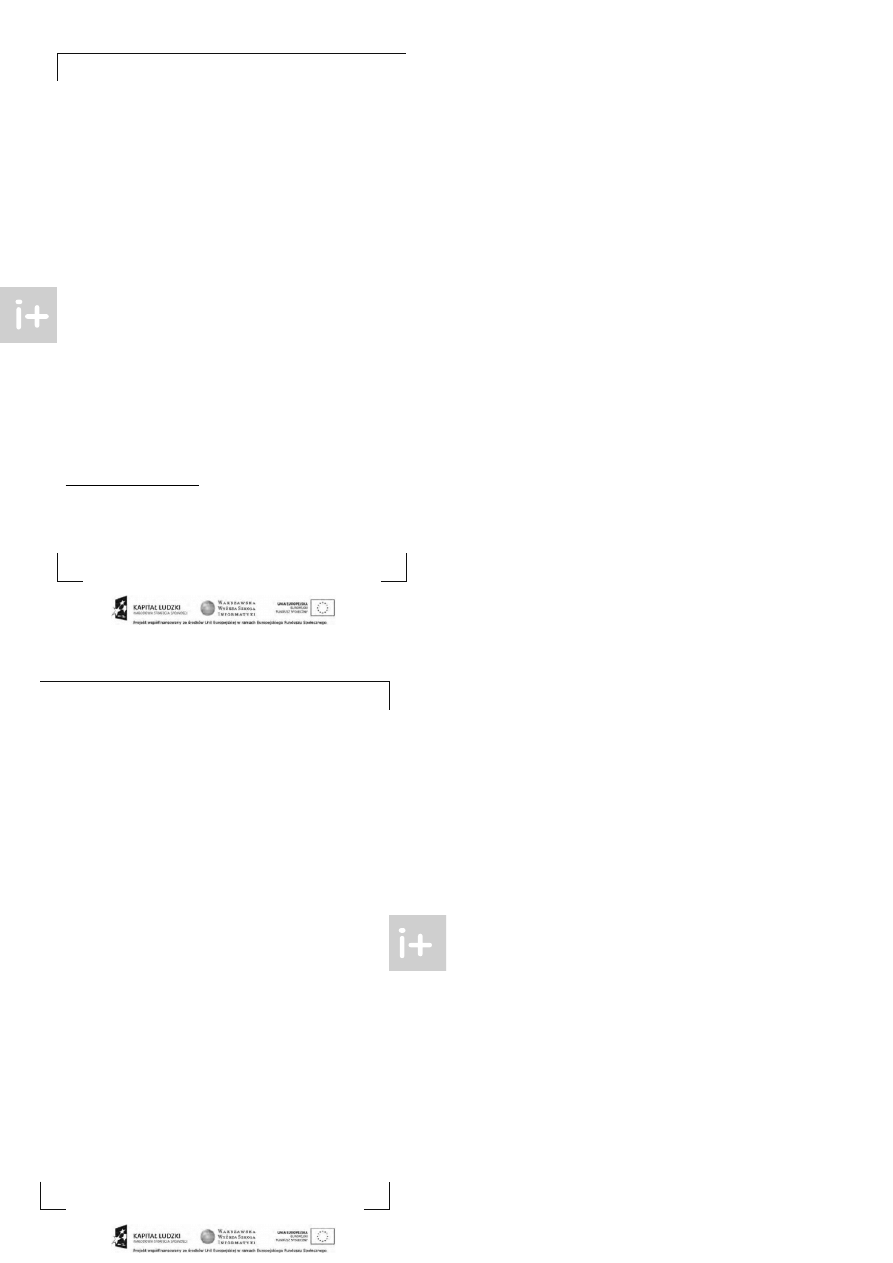
D e fi n icj a 4. K op cem nazywamy pełne drzewo binarne z wart ościami w wierzchołkach,
kt óre ma własność kop ca, t zn. każdy wierzchołek ma przypisaną wart ość nie większą niż
wart ości jego synów.
Innymi słowy, dla wszyst kich x zachodzi heap[ x/ 2 ]
heap[x].
2
3
5
3
6
7
6
8
4
9
8
7
Rys.2: Przykł adowy kopiec
Op er acj e na kop cu
Niekt óre operacje na kopcu oprócz opisu b ędą zawierały implement ację. Na pot rzeby implemen-
t acji zakładamy, że nasz kopiec ma nast ępującą deklarację:
#def i ne MAXN 1000000
i nt heap[ MAXN+1] ;
> Struktury danych i ich za stosowania
< 11 >
i nt si ze=0; / / l i czba el ement ów w kopcu
/ / el ement y w kopcu t o heap[ 1] , heap[ 2] , . . . , heap[ si ze]
W st a w ia n ie e lem en t u
Aby wst awić element do kopca:
1. doda jemy nowy element na koniec t ablicy (własność kopca może być zaburzona)
2. dopóki ojciec nowego element u jest od niego większy, t o zamieniamy wart ości w obu wierz-
chołkach (proces t en nazywamy kop cow a n ie m w gór ę ( H ea p U p ) )
voi d heapUp( i nt x) { / / kopcuj e w gór ę el ement na pozycj i x
whi l e( heap[ x/ 2] > heap[ x] ) {
swap( heap[ x] , heap[ x/ 2] ) ; / / zami eni a war t ości w obu węzł ach
x/ =2;
}
}
voi d i nser t ( i nt x) { / / dodaj e x do kopca
heap[ ++si ze] =x;
heapUp( si ze) ;
}
Z n a jd ow a n ie m in im u m
Minimum zna jduje się oczywiście z korzeniu, czyli w heap[ 1] .
i nt mi ni mum( ) { / / zwr aca mi ni mum
r et ur n heap[ 1] ;
}
U su wa n ie kor z en ia
Aby usunąć korzeń z kopca:
1. w miejsce korzenia wst awiamy ost at ni element z t ablicy (własność kop ca może być zabu-
rzona)
2. dopóki wst awiony element jest większy od kt óregoś ze swoich synów t o zamieniamy go z sy-
nem o mniejszej wart ości (proces t en nazywamy kop c ow a n ie m w d ół ( H e a p D ow n ) )
Usuwanie korzenia dobrze wizualizuje prezent acja dołączona do t ego t emat u.
voi d heapDown( i nt x) { / / kopcuj e w dół el ement na pozycj i x
whi l e( 2* x <= si ze) { / / dopóki x ma choci aż j ednego syna
i nt son=2* x;
i f ( 2* x+1 <= si ze && heap[ 2* x+1] < heap[ 2* x] )
son=2* x+1;
/ / zmi enna son zawi er a t er az i ndeks syna x o mni ej szej war t ości
i f ( heap[ son] >= heap[ x] ) br eak;
swap( heap[ x] , heap[ son] ) ; / / zami eni a war t ości w obu węzł ach
x=son;
}
}
voi d er aseRoot ( ) { / / usuwa kor zeń ( czyl i mi ni mum)
heap[ 1] =heap[ si ze- - ] ;
heapDown( 1) ;
}
< 12 >
Informatyka +
U su w a n ie d ow oln ego ele m e n t u
Aby usunąć dowolny element (niekoniecznie korzeń) z kop ca:
1. w miejsce usuwanego element u wst awiamy ost at ni element
2. kopcujemy nowy element w górę
3. kopcujemy nowy element w dół
A n a liz a zł ożon ości
W szyst kie opisane op eracje działa ją w czasie prop orcjonalnym do wysoko-
ści kop ca, kt óra jest logaryt miczna względem liczby element ów w kopcu.
Sor t owanie pr zez kop cowanie — H eapSor t
Kop ca można użyć do szybkiego — O(n log n) — sort owania. P omysł jest dość prosty — element y
t ablicy, kt órą chcemy posort ować wrzucamy do kopca a nast ępnie dopóki kopiec nie jest pust y, t o
wypisujemy minimum i je usuwamy.
4.1
Zast osowanie kop ca w im pl em ent acj i algor y t mu D ij k st r y
P r zy p om nieni e algor y t mu
P rzypomnijmy, że algoryt m Dijkst ry służył do zna jdowania na jkrót szych ścieżek ze źródła w sie-
ciach, w kt órych wagi krawędzi są nieujemne.
1
Ot o schemat t ego algoryt mu:
1. oznacz wszyst kie wierzchołki jako nieodwiedzone
2. dla każdego v ∈ V przyjmij di s[v] = ∞
3. przyjmij di s[s] = 0
4. dop óki ist nieje nieodwiedzony wierzchołek o skończonej odległości:
(a) niech v b ędzie wierzchołkiem nieodwiedzonym o na jmniejszej odległości
(b) oznacz v jako odwiedzony
(c) zrelaksuj wszyst kie krawędzie wychodzące z v
Kluczowa jest t ut a j operacja 4.a, kt órą wykonujemy O(|V |) razy a dotychczas zabierała ona
czas O(|V |), co dawało całkowit ą złożoność algoryt mu O(|V |
2
)
Zast osowani e kop ca
Będziemy przechowywać w kopcu numery wierzchołków nieodwiedzonych. Chcielibyśmy zna jdować
szybko w kopcu wierzchołek o na jmniejszej wart ości w t ablicy di s. P rzy kop cowaniu musimy więc
porównywać odpowiednie wart ości w t ablicy di s, a nie bezpośrednio wart ości t rzymane w kopcu
(di s[x] będziemy nazywać prioryt et em wart ości x).
P rioryt et y mogą jednak ulegać zmianie w t rakcie działania algoryt mu (na skut ek relaksacji
krawędzi), co może zaburzyć własność kopca. Zauważmy jednak, że mogą one t ylko maleć.
1
Dokł adniejszy opis znaj duje się w not at kach do kursu „ Pr zegląd podst awowych algor yt mów”
> Struktury danych i ich za stosowania
< 13 >
R ozw iązanie pr oblemu — I m et oda
Za każdym razem, gdy prioryt et jakiegoś element u się zmniejszy, musimy wykonać kop cowanie
t ego element u w górę. Umiemy jednak wykonywać kopcowanie jedynie element u na danej pozycji
(a nie o danej wart ości). P roblem t en da się rozwiązać rozbudowując nieznacznie st rukt urę naszego
kopca.
Oprócz t ablicy heap, będziemy t rzymali t ablicę wher e, gdzie wher e[ x] oznacza pozycję w
kopcu wart ości x, t zn. heap[wher e[x]] = x. P rzyjmujemy wher e[x] = 0, jeśli w kopcu nie ma
element u x. Tablicę t ę musimy uakt ualniać za każdym razem, gdy przemieszczamy elementy w
kop cu. Rozwiązanie t o nie jest perfekcyjne. Musimy zaimplement ować kopiec z op eracją zmiany
prioryt et u, co może za jąć dość dużo czasu, nie są b owiem dost ępne żadne got owe implement acje
kop ca dysponujące t aką operacją.
R ozw iązanie pr oblemu — I I m et oda
P rzedst awimy t eraz rozwiązanie, kt óre korzyst a ze zwykłego kopca (bez operacji zmiany priory-
t et u). Do kop ca b ędziemy wrzucać pary post aci (di s[x], x) — a nie pojedyncze liczby jak dotych-
czas, przy czym przyjmujemy porządek leksykograficzny na parach, t zn.
(x, y) < (a, b) ⇐⇒ x < a ∨ (x = a ∧ y < b)
Na jmniejszy element w kopcu, odp owiada wówczas wierzchołkowi o na jmniejszej odległości.
Co zrobić, jeśli wart ość di s[x] się zmieni? Wrzucamy wówczas do kopca nową parę (di s[x], x).
P rzy t akim p odejściu w kop cu będą zna jdowały się śmieci — nieakt ualne pary p ost aci (d, x), gdzie
d > di s[x]. P ary t akie p o prost u p omijamy przy wyciąganiu ich z kopca.
A ot o dokładniejszy schemat t akiego algoryt mu:
1. dla każdego v ∈ V ust aw di s[v] = ∞
2. ust aw di s[s] = 0
3. wrzuć do kop ca parę (0, s)
4. dopóki kopiec nie jest pusty
(a) wyciągnij na jmniejszą parę z kopca, oznaczmy ją przez (d, v)
(b) jeśli d > di s[v], t o powróć do pkt . 4
(c) zrelaksuj wszyst kie krawędzie wychodzące z v, jeśli poprawia t o odległość do wierzchołka
x, t o doda j parę (di s[x], x) do kopca
Zł ożoność i im plem ent acj a
Oba przedst awione rozwiązania ma ją złożoność O(|E | log |V |), czyli dużo lepszą niż algoryt m Dijk-
st ry nie korzyst a jący z kopca, o ile t ylko ilość krawędzi w grafie jest dużo mniejsza od |V |
2
(grafy
t akie nazywamy rzadkimi). W zadaniach olimpijskich częst o mamy do czynienia z t akimi grafami
a nawet z grafami dla kt órych maksymalne liczby krawędzi i wierzchołków są t ego samego rzędu.
Implement ację algoryt mu Dijkst ry z użyciem kop ca p ozost awiam jako wart ościowe ćwiczenia.
Być może zast anawiasz się, jak reprezent ować w programie pary. Na jwygodniejszą opcją jest sko-
rzyst anie z klasy pai r . P oniższy kod prezent uje sposób jej używania:
#i ncl ude <st di o. h>
/ / poni ższe dwa wi er sze są koni czne do kor zyst ani a z kl asy pai r
#i ncl ude <i ost r eam>
usi ng namespace st d;
i nt mai n( ) {
< 14 >
Informatyka +
pai r <i nt , i nt > par a; / / t wor zy zmi enną par a, kt ór ej obi e skł adowe są t ypu i nt
par a. f i r st =7; / / ust awi a pi er wszą skł adową na 7
par a. second=5; / / ust awi a dr ugą skł adową na 5
pr i nt f ( " %d %d\ n" , par a. f i r st , par a. second) ; / / wypi sze " 7 5"
par a=make_pai r ( 2, 3) ; / / szybsza opcj a na pr zypi sani e obu war t ości
pai r <i nt , i nt > cos( 2, 3) ; / / pr zypi sani e war t ości pr zy t wor zeni u
i f ( par a < cos) { / / par y są por ównywane w por ządku l eksykogr af i cznym!
cos = par a;
}
r et ur n 0;
}
5
D r zewa r ozpi naj ące
Rozważmy nast ępujący problem. J est eśmy na ob ozie informat ycznym i mamy za zadanie ut worzyć
sieć przewodową pomiędzy n hubami. Dodat kowo chcemy zużyć do t ego możliwie mało kabla,
kt óry w końcu t eż koszt uje. Nie wszyst kie pary huby da ją się połączyć, gdyż np. są za daleko od
siebie. P omiędzy parami hubów, kt óre możemy połączyć, znamy wymagane długości kabla. Nie
można t worzyć nowych rozgałęzień przy tworzeniu hub ów. W jaki sp osób znaleźć sieć łączącą huby
t ak, aby możliwy był t ransp ort danych między wszyst kimi parami (być może z użyciem hub ów
pośredniczących)? P roponujemy zast anowić się chwilę nad t ym problemem.
R ozwi ązani e
Zacznijmy od obserwacji, że szukana sieć jest drzewem. Gdyby w opt ymalnej sieci były cykle, t o
można by wyrzucić dowolną krawędź z cyklu ot rzymując sieć, kt óra nadal łączy wszyst kie huby,
ale jest krót sza o jedno połączenie (zużywamy mniej kabla).
Kolejna obserwacja jest t aka: zawsze ist nieje opt ymalne drzewo rozpina jące (czyli t akie, kt óre
łączy wszyst kie wierzchołki do jednej spójnej składowej), kt óre zawiera na jkrót szą krawędź. P owód
jest prost y: gdybyśmy znaleźli drzewo o na jmniejszej sumarycznej długości, kt óre nie zawierałoby
t ej na jkrót szej krawędzi, moglibyśmy dodać t ę krawędź do t ego drzewa i uzyskalibyśmy jakiś cykl.
J ak wiemy, możemy wyrzucić z t ego cyklu dowolną krawędź (inną od t ej dopiero co dodanej) i
nadal mieć spójną sieć. P onieważ pewną krawędź zast ą piliśmy inną, o nie większej długości, t o
w sumie nowa długość kabli jest nie większa niż poprzednia.
P r zy k ł ad
P opat rzmy na t aką sieć p ołączeń:
3
5
7
2
4
1
6
5
6
1
7
1
2
3
2
1
1
4
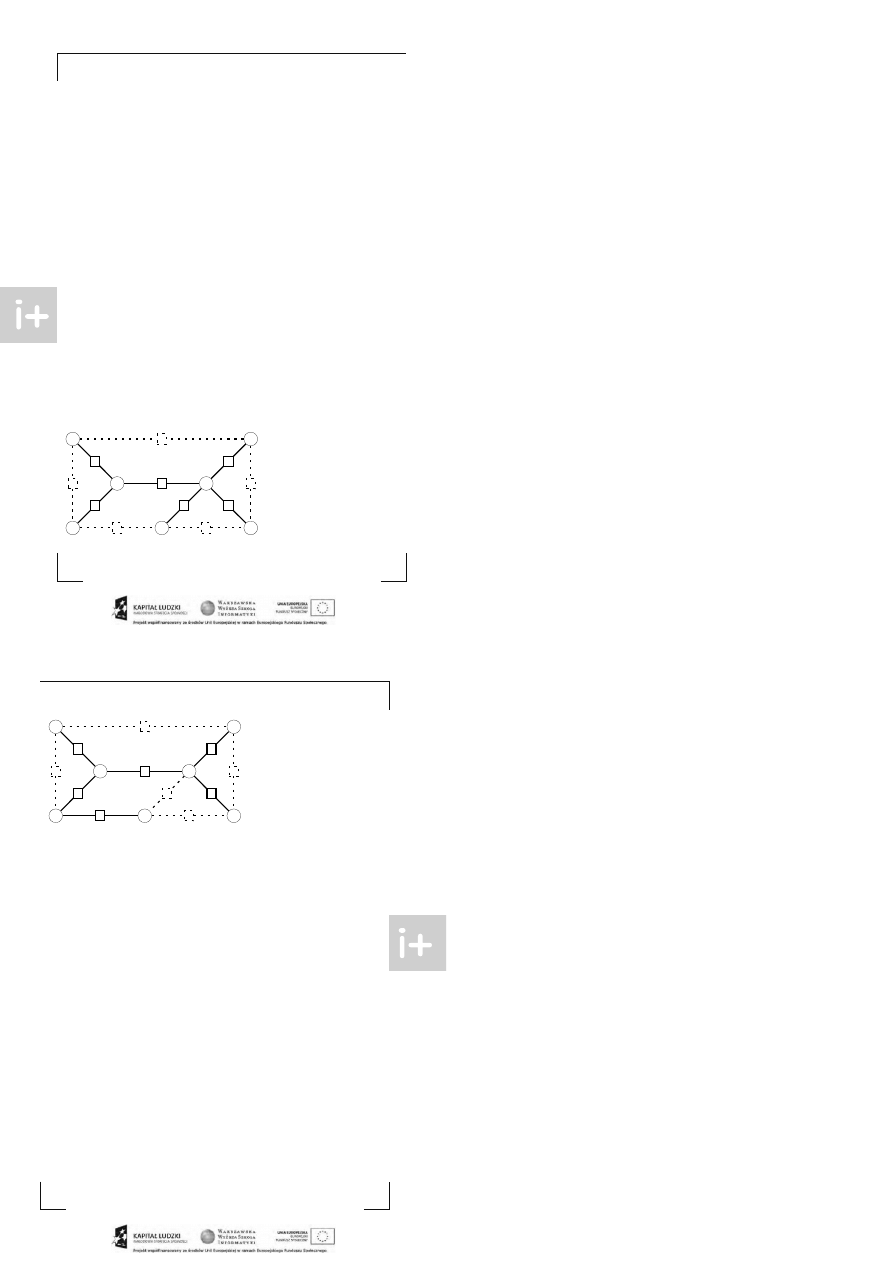
Kt oś wybrał pogrubione krawędzie, uzyskując według siebie na jkrót sze drzewo rozpina jące. Łączna
długość: 13. Spróbuj samemu znaleźć błąd w wyborze krawędzi!
> Struktury danych i ich za stosowania
< 15 >
R ozw ią za n ie : J est cykl 2—3—5—4. W t ym cyklu nie zost ała wybrana t ylko krawędź 3—5,
mimo, że t a krawędź jest na jkrót sza. P odmieniamy ją za na jdłuższą krawędź z t ego, czyli 4—5.
Nowa długość t o 10. Nowe drzewo wygląda t ak:
3
5
7
2
4
1
6
5
6
1
7
1
2
3
2
1
1
4
P onieważ nas int eresuje dowolne drzewo rozpina jące, kt órego długość jest minimalna, t o mo-
żemy z góry wziąć na jkrót szą krawędź i mieć p ewność, że nie zamkniemy sobie drogi do optymal-
nego rozwiązania.
P om y sł 1
Teraz w dość nat uralny sposób nasuwa się p omysł, aby powt órzyć sposób wyboru kolejnej kra-
wędzi. W ybiera jąc nową krawędź omijamy t e, kt órych dodanie spowodowałoby p owst anie cyklu.
Zast anówmy się, dlaczego t o rozwiązanie działa.
K r ok a lgor y t m u
P opat rzmy t rochę inaczej na t en problem. Zna jdujemy na jpierw na jkrót szą krawędź spośród
wszyst kich dozwolonych. Doda jemy ją do wynikowego drzewa. P rzypuśćmy, że łączyła ona wierz-
chołki v i u. Możemy złączyć t e wierzchołki do jednego wierzchołka. W końcu, od moment u dodania
krawędzi v − u nie rozróżniamy już tych wierzchołków. J est nam ob ojęt ne, czy jakaś nowa krawędź
połączy w z v, czy w z u. Z p ołączonego wierzchołka uv wychodzą wszyst kie t e same krawędzie,
kt óre wychodziły wcześniej. P o połączeniu może się p ojawić jakiś wierzchołek, do kt órego idą dwie
krawędzie z wierzchołka uv. Oczywist e jest , że t ę o większej długości usuwamy. Nie będzie już ona
pot rzebna.
K r ok i co d a le j?
P o jednokrot nym wykonaniu operacji wyb oru krawędzi i scaleniu dwóch wierzchołków dost a jemy
nowy problem. Uzyskaliśmy graf o n − 1 wierzchołkach, kt óre t rzeba połączyć drzewem rozpina ją-
cym. P ost ępujemy znów t ak samo. Czyli wykonujemy k r ok a lgor y t m u . Zna jdujemy na jkrót szą
krawędź i łączymy. Robimy t ak, aż nie osią gniemy grafu z jednym wierzchołkiem. St an z jednym
wierzchołkiem oznacza, że wszyst kie wierzchołki są w jednej sp ójnej składowej.
P op r a w n ość
P oprawność t ego algoryt mu wynika st ąd, że przed każdym krokiem mamy problem znalezienia
drzewa rozpina jącego w zwycza jnym grafie, bez żadnych wybranych wcześniej krawędzi. W iemy
nat omiast z wcześniejszych rozważań, że w t akim grafie zawsze ist nieje rozwiązanie, w kt órym
bierzemy na jkrót szą krawędź. Wynika st ąd, że algoryt m, kt óry za każdym razem wybiera na j-
krót szą krawędź i scala końce t ej krawędzi, p oprawnie zna jdzie drzewo rozpina jące o minimalnej
sumarycznej długości.

< 16 >
Informatyka +
A je d n a k P om y sł 1 d zia ł a !
Zauważmy t eraz, że począt kowy algoryt m robi dokładnie t o samo. Zawsze bierzemy na jkrót szą
niewykorzyst aną jeszcze krawędź i doda jemy ją do szukanego drzewa, jeśli jej końce w drzewie
leżą w różnych składowych. W niosek? Ten algoryt m t akże jest p oprawny.
I le t o n a s koszt u je ?
P ozost a je kwest ia, jak szybko można zaimplement ować t en algoryt m. Niech n oznacza ilość wierz-
chołków grafu, zaś m oznacza liczbę krawędzi. Na p ocząt ku wart o posort ować krawędzie wzglę-
dem rosnącej długości, aby pot em wybór kolejnych na jkrót szych był prosty. Ta faza koszt uje nas
O(m log m). Trudniejsza jest kwest ia, jak szybko sprawdzać, czy dwa końce krawędzi leżą w budo-
wanym drzewie rozpina jącym w jednej spójnej składowej. Na jprost sze rozwiązanie, t o sprawdzanie
przy każdej dodawanej krawędzi algoryt mem przeszukiwania grafu, np. met odą DF S, czy końce
krawędzi są w t ej samej spójnej składowej. Takie rozwiązanie prowadzi do złożoności t ej fazy
wynoszącej O(n · m). J est t o bardzo dużo i spróbujemy zredukować t en koszt . Można t o nieco
ulepszyć spost rzeżeniem, że jeśli nie dodaliśmy nowej krawędzi, t o podział na składowe jest cały
czas t en sam. Oznacza t o, że wyst arczy, żebyśmy po każdym dodaniu krawędzi policzyli podział na
składowe. Możemy t o zrobić przypisując wszyst kim wierzchołkom w danej składowej jakąś liczbę
charakt erystyczną. P óźniej łat wo już odpowiadać, czy dwa wierzchołki są w jednej spójnej skła-
dowej. Wyst arczy sp ojrzenie, czy przyporządkowane im liczby charakt eryst yczne są sobie równe.
Takie rozwiązanie w t ej fazie koszt uje O(n
2
) czasu, co jest zauważalnie lepsze niż rozwiązanie
poprzednie, szczególnie, gdy graf jest gęsty.
Znany jest jednak znacznie szybszy sp osób sprawdzania czy wierzchołki są połączone. Met oda
t a korzyst a ze st rukt ury zbiorów rozłącznych.
6
Zbi or y r ozł ączne
Dana jest p ewna rodzina zbiorów. Każde dwa zbiory w t ej rodzinie są parami rozłączne. Na t ej
rodzinie zbiorów chcemy wykonywać dwie operacje. J edna - t o zapyt anie: czy element a i element
b należą do t ego samego zbioru. Druga - t o op eracja połączenia dwóch p odzbiorów w jeden.
Int eresuje nas przede wszyst kim t o, jak szybko działa nasza st rukt ura, jeśli na n element ach
wykonamy n op eracji złączenia zbiorów i m operacji sprawdzenia, czy jakieś dwa element y są
w tym samym zbiorze.
We wszyst kich prezent owanych p oniżej podejściach będziemy wykonywać dwie op eracje:
•
FI ND( x) — znalezienie reprezent anta zbioru, do kt órego należy x. J eśli x i y należą do t ego
samego zbioru, t o FI ND( x) zwraca t o samo, co FI ND( y) .
•
UNI ON( x, y) — złączenie zbioru zawiera jącego x ze zbiorem zawiera jącym y.
Podej ście pier wsze
Każdy zbiór reprezent ujemy w post aci list y element ów. Dodat kowo każdy element ma wskaźnik
do pierwszego element u na liście. W t edy:
•
Op erację FI ND wykonujemy w czasie O(1), wyst arczy odwołać się do pierwszego element u.
•
J eśli chcemy złączyć dwie list y, t o możemy jedną zost awić t aką jaką jest , a drugą dołączyć
na koniec. Na razie koszt owało nas t o czas O(1). Niest et y musimy jeszcze p oprawić wart ości
wskaźników drugiej listy t ak, aby p okazywały na pierwszy element pierwszej list y. To koszt uje
znacznie więcej, bo O(d), gdzie d jest długością drugiej listy. Rozważmy na jgorszy scenariusz:
mamy jeden duży zbiór, kt óry za każdym razem dołączamy do listy jednoelement owej na
> Struktury danych i ich za stosowania
< 17 >
koniec. Wt edy i - t a t aka operacja koszt uje i modyfikacji wskaźnika. Oznacza t o, że wykonanie
n t akich op eracji wykonamy będzie t rwało:
n
i = 1
i =
n(n + 1)
2
czyli O(n
2
).
W szyst kie zapyt ania i op eracje p ołączenia za jmują razem O(n
2
+ m).
Podej ście dr ugie
Zamiast doklejać drugą list ę na koniec pierwszej, można wybrać kolejność doklejania t ak, aby było
pot em możliwie mało operacji modyfikowania wskaźnika na pierwszy element . W t ym celu zawsze
do dłuższej list y doklejamy krót szą. P owoduje t o, że każdy element , gdy zmieniamy mu wskaźnik
do reprezent ant a, przyna jmniej p odwa ja długość list y, w kt órej się zna jduje. Wniosek jest t aki, że
każdy element b ędziemy poprawiać maksymalnie O(log n) razy. Oznacza t o, że wszyst kie op eracje
połączenia koszt ują nas n · O(log n) = O(n log n) plus O(n) operacji łączenia samych list . Razem
da je t o O(n log n). Zapyt ania FI ND koszt ują nas razem O(m).
W sumie działanie naszej st rukt ury będzie koszt ować O(m + n log n). Niby niewielka zmiana,
a złożoność znacznie lepsza.
D o t r zech r azy szt uka
Ost anie podejście b ędzie p odobne. Tym razem reprezent ujemy zbiór jako drzewo. W t akim drzewie
każdy element będzie miał wskaźnik na swojego ojca. Dodat kowo każdy b ędzie pamięt ał wysokość,
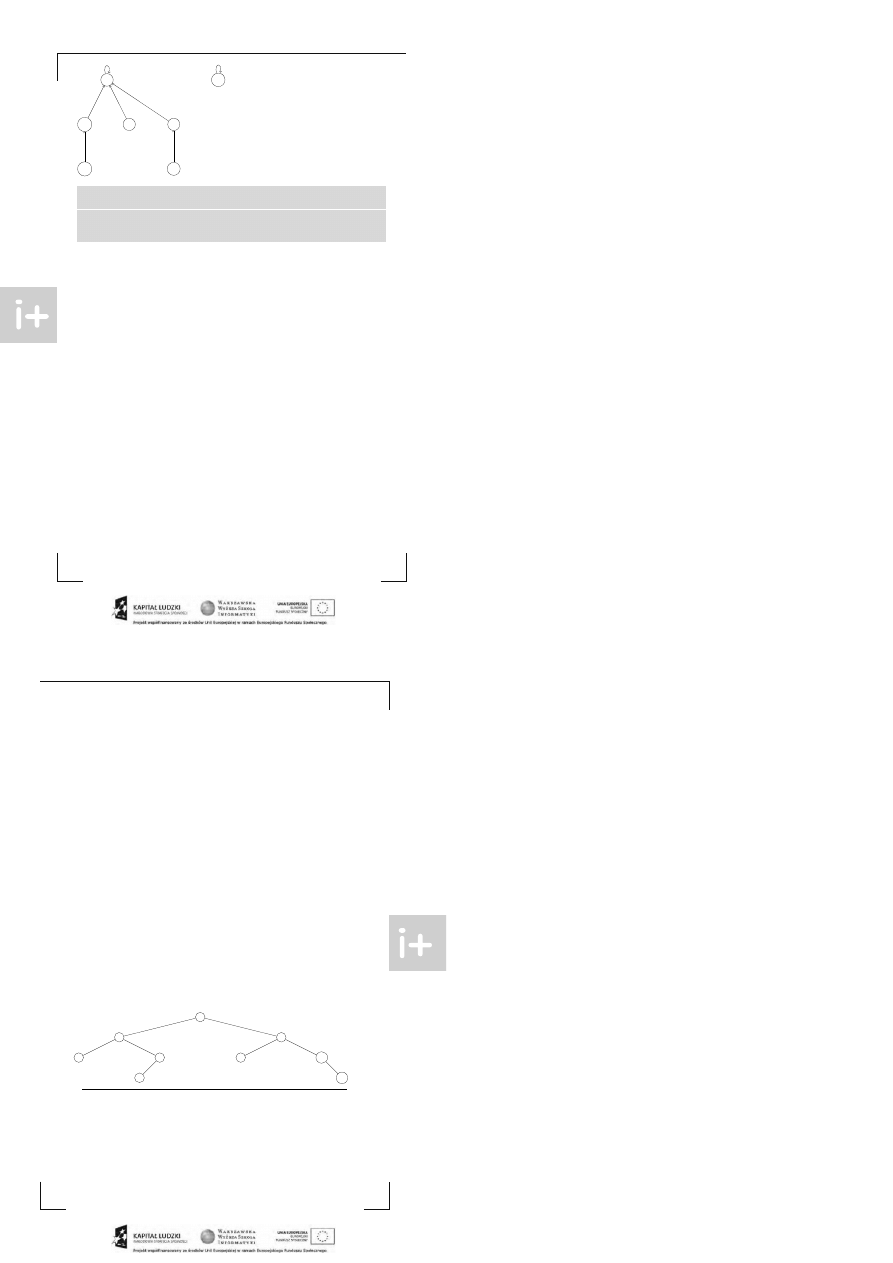
na kt órej się akt ualnie zna jduje. Zasadniczo b ędzie t o wyglądać t ak:
a
b
d
c
e
f
g
J eśli wywołujemy FI ND, t o idziemy po wskaźnikach do góry. J eśli chcemy p ołączyć zbiór
zawiera jący x ze zbiorem zawiera jącym y, t o musimy na jpierw znaleźć reprezent ant ów, czyli
r
x
= FI ND( x) , r
y
= FI ND( y) , a pot em do element u o wyższej randze sp ośród r
x
i r
y
p odpinamy
t en o niższej randze. J eśli przypadkiem rangi były równe, t o zwiększamy rangę t emu element owi,
do kt órego zost ał p odpięt y t en drugi. Efekt przykładowej operacji UNI ON( b, f ) :
< 18 >
Informatyka +
a
b
d
c
e
f
g
Ć w ic zen ie 11. W ykaż, że wysokość t ak skonst ruowanego drzewa jest co na jwyżej lo-
garyt miczna ze względu na liczbę element ów t ego p oddrzewa.
Ć w ic zen ie 12. Napisz procedurę UNI ON i funkcję FI ND. P rzyjmij, że element y ma ją
numery od 1 do n, t ablica f at her reprezent uje ojca w drzewie reprezent ującym zbiór.
Tablica r ank reprezent uje rangę/ wysokość zbioru podczepionego w danym elemencie.
Na razie złożoność czasowa jest bardzo podobna do t ej z p odejścia drugiego. Może t rochę
lepsza st ała, ale nic poza t ym. Teraz p osłużymy się kolejną szt uczką, aby znacząco przyśpieszyć
algoryt m.
S zt u czka
Od t ej pory nazywa jmy pamięt aną wysokość drzewa rangą. Na razie napiszmy funkcję F IND
nast ępująco:
i nt FI ND( i nt x) {
i f ( f at her [ x] == x) r et ur n x;
r et ur n FI ND( f at her [ x] ) ;
}
Ten kod jest poprawny, ale nieopt ymalny. P rzy każdym zapyt aniu o element x musimy pokonać
długą ścieżkę do korzenia. Z p omocą przychodzi nam szt uczka: każdy odwiedzany element pod-
pinamy do reprezent ant a. Zat em jeśli przechodzimy ścieżkę, t o podepnijmy wszyst kie odwiedzane
element y do reprezent ant a. P opat rzmy na nowy kod:
i nt FI ND( i nt x) {
i f ( f at her [ x] == x) r et ur n x;
f at her [ x] = FI ND( f at her [ x] ) ;
r et ur n f at her [ x] ;
}
Oszacowanie złożoności czasowej t ego algoryt mu jest dość t rudne. Zost ało t o opisane w wyczer-
pujący sp osób we „W prowadzeniu do algoryt mów”. Wart o zacyt ować oszacowanie złożoności za
t ą książką: n op eracji łączenia i m operacji F IND koszt ują O(m log
∗
n), gdzie log
∗
n oznacza wy-
sokość st osu pot ęg dwójek p ot rzebnych do zbudowania n. Np. log
∗
2 = 1, log
∗
2
2
= 2, log
∗
2
22
= 3,
log
∗
2
22
2
= 4, it d. Wart ość 2
22
22
= 2
65536
wielokrot nie przewyższa rozmiarem dane, kt óre są prze-
twarzane przez dzisiejsze komput ery. Można więc przyjąć, że czas działania t ego algoryt mu jest
liniowy.
Cała t a szt uczka nosi nazwę kom p r e sji ścież e k .
> Struktury danych i ich za stosowania
< 19 >
Podsum owani e
Korzyst a jąc z przedst awionego algoryt mu na zna jdowanie drzewa rozpina jącego i szybkiej st ruk-
t ury danych rozwiązującej problem F IND-UNION możemy zbudować drzewo rozpina jące o na j-
mniejszej sumarycznej długości w czasie O(m log m).
Cały przedst awiony algoryt m nosi nazwę algoryt mu Kruskala z użyciem st rukt ury danych dla
zbiorów rozłącznych.
7
D r zewa wyszukiwań bi nar nych ( B ST )
P rzy rozwiązywaniu problemów algoryt micznych nat rafiamy częst o na konieczność przechowywa-
nia zbioru (czy raczej mult izbioru), kt órego zawart ość będzie się częst o zmieniała. Zwykle chcemy
wt edy móc st wierdzać, czy element o określonej wart ości w nim wyst ępuje. J aka jest odpowiednia
st rukt ura danych do przechowywania t akiego mult izbioru?
P ierwsze, co przychodzi do głowy, t o zwykła list a. Wówczas jednak szukanie określonej wart o-
ści, może wymagać przejrzenia wszyst kich element ów mult izbioru, co nie jest zbyt wyda jne. Innym
rozwiązaniem jest t rzymanie wart ości w posort owanej t ablicy. Wówczas wyszukiwanie binarne ele-
ment u będzie działało szybko, ale wst awianie nowego element u wymagać będzie bądź ponownego
sort owania, bądź kopiowania pewnej liczby element ów, być może dużej. Ist nieją jednak st rukt ury,
kt óre wszyst kie t e op eracje mogą wykonywać szybko.
D r zewo w y szuk iwań binar ny ch
St rukt ura t a służy do przechowywania element ów uporządkowanych (np. rosnąco), czym różni
się od innych st rukt ur, jak choćby st osu. P o angielsku nazywa się ona binary search tree, st ąd
powszechnie używany skrót BST .
Drzewa BST są ukorzenione (t zn. ma ją jeden wybrany wierzchołek b ędący korzeniem całego
drzewa) oraz binarne (czyli każdy wierzchołek ma co na jwyżej dwóch synów). W każdym wierz-
chołku przechowywane są wart ości, nazywane również k lu cz a m i. T ym, co odróżnia drzewa BST
od, na przykład, kopca jest t o, że klucze wierzchołków spełnia ją dodat kowy warunek:
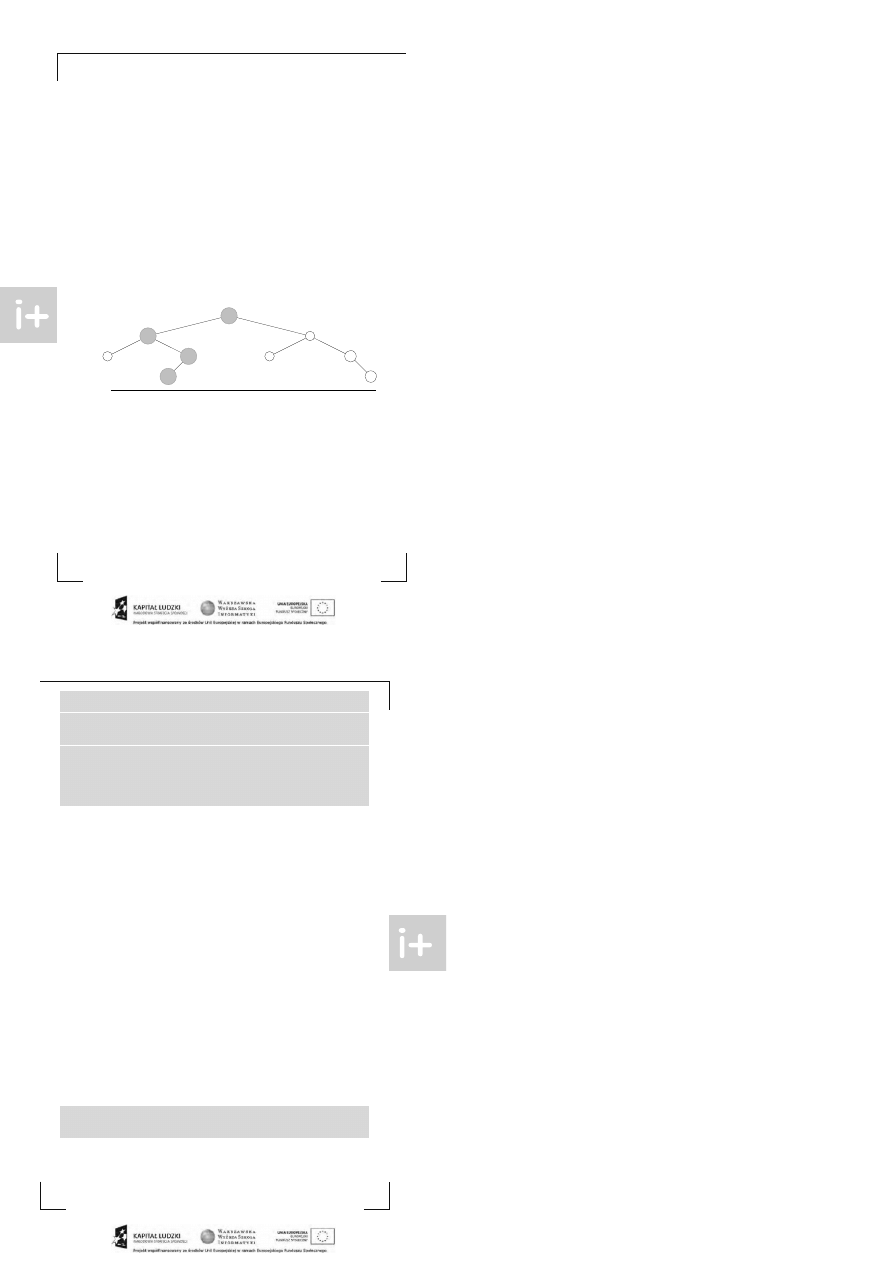
Por ządek symetr yczny: dla każdego wierzchołka o kluczu v wierzchołki w jego lewym
poddrzewie ma ją wart ości mniejsze bądź równe v, a w prawym większe bądź równe.
7
3
9
1
5
8
11
4
12
Rys. 1: Pr zykł adowe drzewo BST
Warunek p orządku symet rycznego pokazuje już, jak będziemy wyszukiwali element ów w drze-
wach BST : jeżeli szukany element jest mniejszy od klucza akt ualnego wierzchołka t o szukamy w
lewym p oddrzewie, w przeciwnym przypadku w prawym.
St r uk t ur a i m pl em ent acj i
Implement acja drzew BST jest t rochę bardziej skomplikowana od kop ca, gdyż nie można używać
po prost u jednej t ablicy. Zamiast niej, p odobnie jak w przypadku st osów, kolejek i list , będziemy
korzyst ać ze st rukt ur dla wierzchołków i łączyć je wskaźnikami.
< 20 >
Informatyka +
st r uct Node
{
/ / Wskaźni ki do l ewego i pr awego syna, or az oj ca.
/ / war t ość NULL oznacza br ak odpowi edni ego wi er zchoł ka.
Node * l ef t , * r i ght , * par ent ;
i nt key; / / kl ucz, czyl i war t ość pr zechowywana w wi er zchoł ku
} ;
Całe drzewo będziemy przechowywali w programie jako obiekt :
st r uct BST
{
Node * r oot ; / / wskaźni k na kor zeń dr zewa
BST( )
/ / konst r ukt or pust ego dr zewa
{
r oot = NULL;
}
/ * t u nal eży umi eszczać kol ej ne f unkcj e * /
} ;
W y szuk iwani e elem ent u
Skoro znamy już st rukt urę drzewa BST możemy zaimplement ować wyszukiwanie element u w drze-
wie. Algoryt m oparty na met odzie dziel i zwycięża j, zost ał już p obieżnie opisany: poczyna jąc od
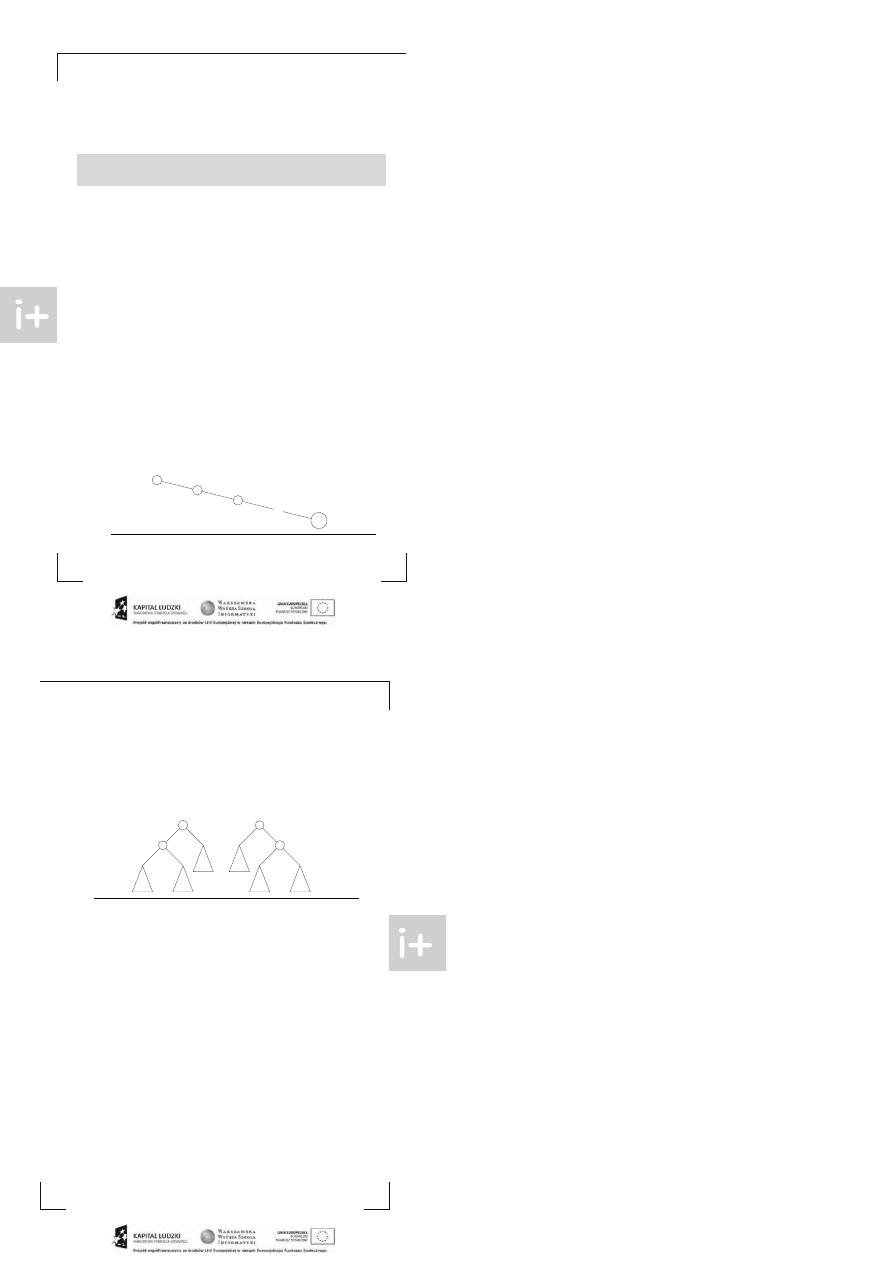
całego drzewa sprawdzamy korzenie kolejnych poddrzew: jeżeli klucz t akiego korzenia jest większy
od p oszukiwanego t o kontynuujemy w lewym poddrzewie, w przeciwnym przypadku w prawym.
7
3
9
1
5
8
11
4
12
Rys. 2: Poszukiwanie element u o kluczu 4
Node * sear ch( i nt v)
{
Node * s = r oot ;
/ / gdy s == NULL, oznacza t o, że wyszl i śmy , , poza dr zewo’ ’
whi l e ( s ! = NULL && s- >key ! = v) {
i f ( s- >key > v)
s = s- >l ef t ;
el se
s = s- >r i ght ;
}
r et ur n s;
/ / f unkcj a zwr aca NULL, gdy br ak wi er zchoł ka o kl uczu v
}
Nie t rudno jest zauważyć, że met oda t a t ak na prawdę przechodzi po jakiejś ścieżce w drzewie,
odwiedza jąc każdy wierzchołek raz. J ej złożoność czasowa t o zat em O(h), gdzie h jest wysokością
drzewa (czyli długością na jdłuższej ścieżki z korzenia do liścia).
> Struktury danych i ich za stosowania
< 21 >
Ć w iczen ie 13. Wymyśl i zaimplement uj algoryt m zna jdujący na jmniejszy klucz w drze-
wie BST .
Ć w iczen ie 14. W jakiej kolejności należałoby odwiedzać, wierzchołki drzewa, by ich
klucze przeglądać w kolejności niemalejącej? Napisz met odę klasy BST wypisującą
wszyst kie klucze z drzewa w kolejności niemalejącej.
Ć w iczen ie 15. N a st ę p n ik iem wierzchołka s nazywamy wierzchołek, kt óry zost anie
wypisany t uż po s, w p owyższym algoryt mie przeglądania drzewa. W ykaż, że jeżeli s
ma prawego syna, t o nast ępnikiem s jest wierzchołkiem o na jmniejszym kluczu w jego
prawym p oddrzewie. Zaimplement uj funkcję zna jdującą nast ępnik w t akim przypadku.
Kt óry wierzchołek jest nast ępnikiem s, gdy nie ma on prawego p oddrzewa? Czy nast ęp-
nik b ędzie zawsze ist niał?
D odawani e elem ent u
J eżeli chcemy by nasze drzewa okazały się użyt eczne musimy nauczyć się dodawać do nich nowe
wierzchołki t ak, by zost ał zachowany porządek symet ryczny. W tym celu należy, naśladując algo-
ryt m wyszukiwania element u, przejść przez drzewo, aż do wierzchołka, kt óry nie ma odp owiedniego
(prawego lub lewego) syna i dodać t am nowy wierzchołek.
voi d i nser t ( i nt v)
{
Node * n = new Node( ) , * s = r oot , * pr ev = NULL;
/ / i ni cj al i zacj a nowego wi er zchoł ka
n- >l ef t = NULL;
n- >r i ght = NULL;
n- >key = v;
whi l e ( s ! = NULL) {
/ / naśl adowani e wyszuki wani a
pr ev = s;
i f ( s- >key >= v)
s = s- >l ef t ;
el se
s = s- >r i ght ;
/ / Ni ezmi enni k: zmi enna pr ev wskazuj e
/ / na popr zedni o odwi edzony wi er zchoł ek
}
/ / pod wi er zchoł ek pr ev dowi ązuj emy n z odpowi edni ej st r ony
i f ( pr ev- >key >= v)
pr ev- >l ef t = n;
el se
pr ev- >r i ght = n;
n- >par ent = pr ev;
}
Ć w iczen ie 16. P owyższy kod działa jedynie dla drzewa o co na jmniej jednym elemencie.
Dlaczego? Co się st anie gdy zost anie uruchomiona na pust ym drzewie? Dopisz do met ody
obsługę t ego sp ecjalnego przypadku.
U suwani e wi er zchoł ka
Usuwanie wierzchołka jest t rochę bardziej skomplikowane od dodawania, gdyż t rzeba uważać
na więcej przypadków szczególnych. J eżeli chcemy usunąć wierzchołek s, t o musimy zadbać o p o-
prawne działanie w nast ępujących przypadkach:
< 22 >
Informatyka +
1. s nie ma synów — możemy po prost u skasować t en wierzchołek;
2. s ma jednego syna (lewego lub prawego). Wówczas ojcu s jako bezpośredniego pot omka (i t o
p o odpowiedniej st ronie!) ust awiamy jedynego syna s;
3. s ma dwóch synów. Należy wówczas znaleźć nast ępnika s, jego klucz zapisać w wierzchołku s
i usunąć nast ępnika. Zauważmy, że operacja t a nie zaburza porządku symet rycznego w drze-
wie, gdyż nast ępnik ma na jmniejszy klucz, nie większy niż t en usuwany.
Napisanie b ezbłędnie met ody z t aką liczbą możliwych przypadków st anowi p ewne wyzwanie,
do kt órego podjęcia zachęcamy!
Ć w ic zen ie 17. Uzupełnij p oniższą met odę t ak, by poprawnie działała we wszyst kich
przypadkach. Nie zapomnij o poprawieniu wskaźników par ent oraz o tym, że usuwany
wierzchołek może być korzeniem drzewa!
voi d er ase( Node * s) {
Node * next ;
i f ( s- >l ef t == NULL | | s- >r i ght ==NULL)
{
/ / pr zypadki 1 i 2: s ni e ma co naj mni ej j ednego syna
/ / popr awni e r ozpat r z t e dwa pr zypadki !
del et e s;
}
el se
{
/ / pr zypadek 3, szukani e nast ępni ka
next = s- >r i ght ;
whi l e ( next - >l ef t ! = NULL)
next = next - >l ef t ;
s- >key = next - >key;
er ase( next ) ;
/ / dzi ęki powyższemu odwoł ani u t r zeba spr awdzi ć mni ej pr zypadków
}
}
7.1
Zr ównoważone dr zewa p oszuk iwań
P r oblem z efek t y w nością dr zew B ST
Operacje dodawania, usuwania i wyszukania na drzewach BST działa ją w czasie proporcjonal-
nym do wysokości drzewa. W przypadku danych losowych, wysokość t a jest rzędu O(log n), co
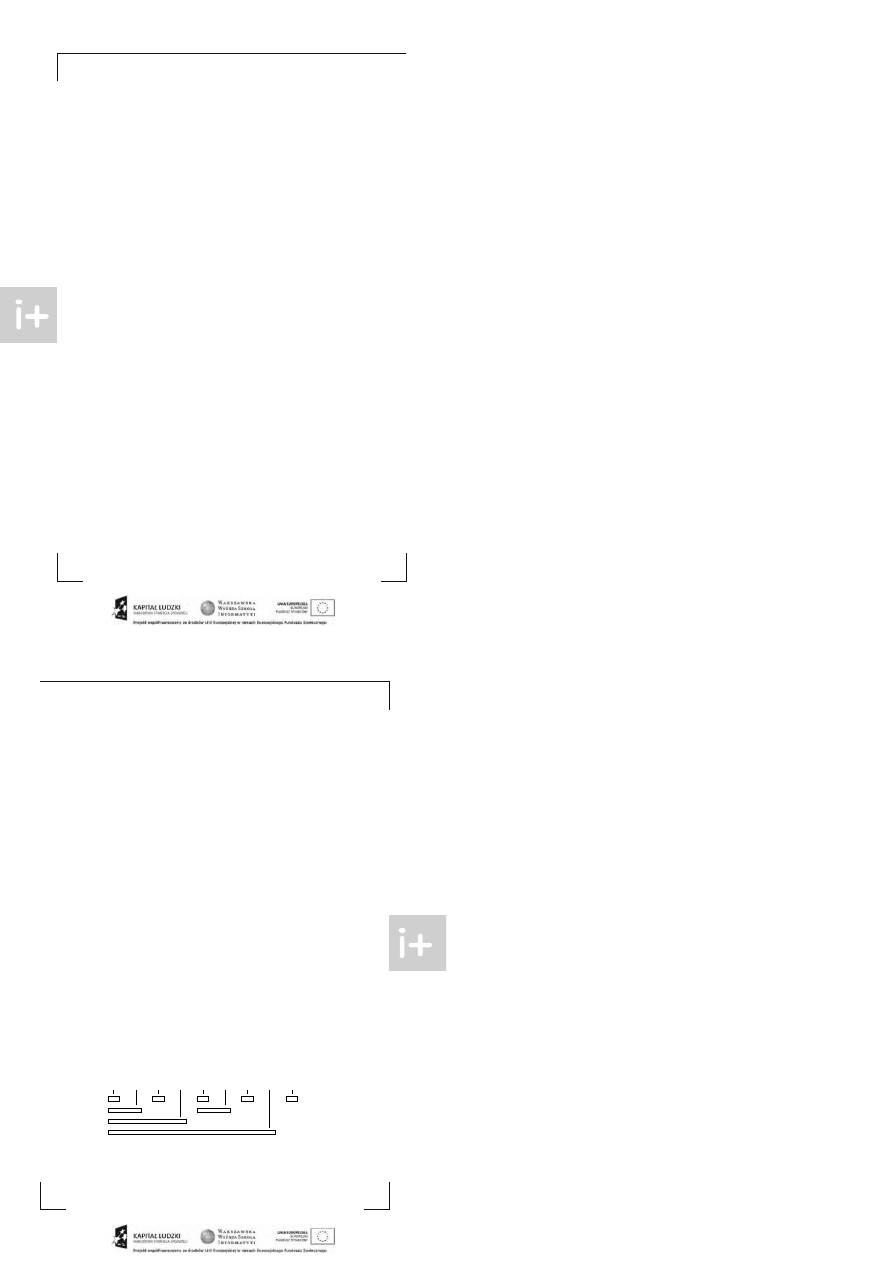
jest zup ełnie zadowala jące. Niest ety, może się zdarzyć, że ciąg element ów dodawanych do drzewa
spowoduje, że b ędzie miało ono p ost ać jednej długiej ścieżki bez rozgałęzień, jak na rysunku 3.
1
2
3
...
1000
Rys. 3: Zł ośliwy przypadek dr zewa BST
Wówczas czas działania wszyst kich operacji na drzewie będzie liniowo zależny od liczby ele-
ment ów, a zat em nic nie zyskujemy na korzyst aniu z drzew BST w porównaniu do zwykłej list y!
> Struktury danych i ich za stosowania
< 23 >
D r zewa AV L
Aby up orać się z powyższym problemem st osuje się różne t echniki. Chyba na jprost szą do zrozu-
mienia są drzewa AVL, zaproponowane przez Gieorgija Adelson-W ielskija i J ewgienija Łandisa.
P omysł p olega na dodaniu drzewom BST nast ępującego warunku:
dla każdego wierzchołka, wysokości jego prawego i lewego p oddrzewa mogą różnić się
o co na jwyżej 1
Można udowodnić, że wysokość drzewa o n wierzchołkach spełnia jącego t en warunek jest O(log n).
Operacje na drzewach AVL są podobne do t ych na BST . Różnica jest t ylko t aka, że po ope-
racjach dodawania, bądź usuwania wierzchołków, kt óre mogą zmienić st rukt urę drzewa, należy
przywrócić warunek zrównoważania. Można t o zrobić za p omocą t zw. rot acji, kt órym przyjrzymy
się na przykładzie z rys. 4.
y
x
A
B
C
y
x
A
B
C
Rys 4. Poj edyncza r ot acj a
Załóżmy, że poddrzewo A ma wysokość h + 1, a poddrzewa B i C ma ją wysokości h. Wówczas w
wierzchołku x poddrzewa różnią się wysokością o 1, co jest dopuszczalne, ale już w wierzchołku y
wysokości p oddrzew różnią się o 2. P ojedyncza rot acja, przedst awiona na obrazku, może t o jednak
poprawić: p o jej wykonaniu poddrzewa b ędą miały równe wysokości, zarówno x jak i y.
J est t o oczywiście bardzo ogólny opis działania drzew AVL. Zaint eresowanych odsyłamy do
pozycji [2] i [3]. Ist nieją t eż inne sposoby równoważenia drzew binarnych. J ako szczególnie prost e do
implement acji polecamy samoorganizujące się drzewa BST (nazywane niekiedy drzewami splay),
o kt órych t eż można poczyt ać w wymienionych mat eriałach.
K ont ener y z bibli ot ek i st andar dowej
J ak się okazuje, w st andardowej bibliot ece szablonów (ST L) języka C + + zna jdują się st rukt ury
danych opart e na zrównoważonych drzewach binarnych. Można z nich korzyst ać w bardzo wielu
przypadkach, ale niest et y nie wszyst kich: czasami t rzeba zaimplement ować swoje własne drzewa.
Dwa częst o st osowane kont enery t ego typu t o set (reprezent uje zbiór, zat em nie mogą się
w nim powt arzać wart ości) oraz mul t i set . Kilka wskazówek, jak się nimi posługiwać:
•
W programie t rzeba umieścić:
#i ncl ude<set >
usi ng namespace st d;
•
Deklaracja zbioru i mult izbioru element ów typu i nt :
set <i nt > zb;
mul t i set <i nt > mzb;
•
Dodawanie, usuwanie i szukanie element u:
< 24 >
Informatyka +
zb. i nser t ( 6) ;
zb. er ase( 7) ;
i f ( zb. f i nd( 4) ! = zb. end( ) )
{
/ / 4 j est w zbi or ze zb
}
•
W ypisanie element ów zbioru w kolejności rosnącej:
f or ( set <i nt >: : i t er at or i t = zb. begi n( ) ; i t ! = zb. end( ) ; ++i t )
pr i nt f ( " %d\ n" , * i t ) ;
W ięcej o korzyst aniu z tych oraz innych kont enerów bibliot eki ST L będzie można dowiedzieć się
na innych kursach. Można t eż korzyst ać z dokument acji (w języku angielskim) dost ępnej pod ad-
resem: ht t p: / / www. sgi . com/ t ech/ st l /
Zadanie
A. P r z ed zia ł y
Napisz program przechowujący informacje o zbiorze przedziałów na prost ej. Będzie on ot rzy-
mywał kolejne polecenia do wykonania, w jednej z p oniższych post aci:
•
1 p k — dodanie do zbioru przedziału o począt ku w p i końcu w k (p i k b ędą liczbami
całkowit ymi, − 10
9
p < k
10
9
).
•
0 — zapyt anie o liczbę rozł ącznych przedziałów w zbiorze,
•
− 1 — koniec listy p oleceń.
Przykł adowe wejście:
1 1 2
1 3 4
0
1 2 3
0
− 1
Pr zykł adowe wyj ści e:
2
1
8
D r zewa pr zedział owe
Czy m są dr zewa pr zedział owe?
D r ze wa m i p r zed zia ł ow y m i nazywamy st rukt ury danych, umożliwia jące szybkie wykonywanie
op eracji na zbiorze przedziałów, t akich jak:
•
wst awienie przedziału do zbioru (być może z pewną wagą),
•
usunięcie przedziału,
•
sprawdzenie w ilu przedziałach zawiera się dany punkt ,
•
odczyt anie sumarycznej wagi punkt ów z danego przedziału, et c.
Na wykładzie przedst awiamy dwa podejścia do implement acji drzewa przedziałowego. P ierwsze
z nich nazywane jest również d r ze w e m p ot ę gow y m .
> Struktury danych i ich za stosowania
< 25 >
U st aleni a wst ępne
Zakładamy, że wszyst kie rozważane przedziały ma ją końce w punkt ach całkowit oliczbowych z
ust alonego zakresu będącego p ot ęgą dwójki (zakres t en oznaczać będziemy przez N ). Inaczej niż
w geomet rii, przez długość przedziału rozumiemy liczb ę punkt ów o współrzędnych całkowitych w
nim zawart ych. P rzykładowo przedział [3, 3] ma długość 1 gdyż zawiera dokładnie jeden punkt .
Łat wiej jest zat em myśleć o punkt ach jak o komórkach t ablicy.
Zakres współrzędnych przedziałów przechowywanych w drzewie nie może być zbyt duży, w
szczególności t ablica liczb całkowitych o rozmiarze 2N (a na jczęściej kilka t akich t ablic) musi
swobodnie mieścić się w limicie pamięciowym. W niekt órych przypadkach możemy p oradzić sobie
z bardzo dużym zakresem przedziałów st osując pewną szt uczkę. J eśli int eresuje nas jedynie uło-
żenie przedziałów względem siebie (a nie ich fakt yczna długość) możemy wst ępnie wczyt ać dane
wejściowe, posort ować wszyst kie wyst ępujące w nich punkt y i nadać im nowe wsp ółrzędne będące
kolejnymi liczbami nat uralnymi. P o t akim zabiegu zakres wsp ółrzędnych będzie wielkości danych
wejściowych.
Każda z omawianych st rukt ur danych będzie udost ępniać dwie operacje:
•
w st a w ie n ie (funkcja i nser t ( ) ) — wykonanie p ewnej akcji (dodanie obciążenia lub wycią-
gnięcie maksimum) na przedziale lub w punkcie,
•
za p y t a n ie (funkcja quer y( ) ) — odczyt anie akt ualnego st anu (sumy lub maksimum) z prze-
działu lub punkt u, będącego wynikiem wykonanych operacji i nser t .
8.1
D r zewo p ot ęgowe
Załóżmy, że pot rzebujemy st rukt ury danych umożliwia jącej wykonywanie nast ępujących operacji:
•
i nser t ( x, v) — dodanie wart ości (inaczej obciążenia) v do punkt u x
•
quer y( a, b) — zsumowanie obciążeń punkt ów zawartych w przedziale [a, b]
Trywialną realizacją powyższych wymagań może być t ablica, w kt órej p o prost u zapisujemy
wst awione wart ości. Niest ety, pomimo t ego, iż funkcja i nser t działa w czasie st ałym, zliczenie
sumy liczb w przedziale wiąże się z koszt em prop orcjonalnym do jego długości, co w przypadku
dużej liczby wywołań quer y dla długich przedziałów jest zdecydowanie zbyt wolne.
Drzewo pot ęgowe opiera się na pomyśle, aby w t ablicy (nazwijmy ją l oad) nie przechowywać ob-
ciążenia jednego punkt u, lecz sumę obciążeń t rochę większego obszaru. Dokładniej, w polu l oad[ x]
będziemy pamięt ać sumę wszyst kich op eracji i nser t dla punkt ów z przedziału [x − p+ 1, x], gdzie
p jest na jwiększą p ot ęgą dwójki dzielącą x.
1
2
3
4
5
6
7
8
9
. . .
Co nam da je t aka modyfikacja? Na pewno komplikuje op erację i nser t , gdyż doda jąc wart ość
do pewnego punkt u musimy uakt ualnić pot encjalnie wiele pól t ablicy. P rzykładowo, wykonując
i nser t w punkcie nr 3 musimy uakt ualnić pola l oad[ 3] , l oad[ 4] , l oad[ 8] , l oad[ 16] , itd. Oka-
zuje się jednak, że liczba niezbędnych zmian jest niewielka.

< 26 >
Informatyka +
Ć w ic zen ie 18. Uzasadnij, że liczba pól t ablicy wymaga jących akt ualizacji przy operacji
i nser t jest rzędu O(log N ).
Skąd wiadomo, kt óre pola w t ablicy uakt ualnić? Zauważmy, że jeśli uakt ualniliśmy p ole o in-
deksie x, a p jest na jwiększą pot ęgą dwójki dzielącą x, t o nast ępnym polem, kt óre “ob ejmie swoim
zasięgiem” p ole x, jest x + p. Wyst arczy zat em zacząć od ust awienia wart ości p ola l oad[ x] , a na-
st ępnie przesuwać się do kolejnych pól, za każdym razem zwiększa jąc indeks o na jwiększą pot ęgę
dwójki dzielącą indeks p ola akt ualnego.
No dobrze, a jak w t akim razie wyznaczyć t ę pot ęgę dwójki? Można t o zrobić łat wo w złożoności
logaryt micznej, my jednak chcielibyśmy umieć wykonać t o w czasie st ałym. Z pomocą przychodzą
op erat ory bit owe, dzięki kt órym szukaną liczbę p wyznaczymy w sposób nast ępujący:
p = ( ( x ^ ( x - 1) ) + 1 ) / 2
Aby lepiej zrozumieć p owyższy wiersz, przeanalizujmy jego działanie na przykładzie.
Niech x = 20, czyli w zapisie binarnym 10100
( 2)
:
x
=
10100
( 2)
x - 1
=
10011
( 2)
x ^ ( x - 1)
=
00111
( 2)
( x ^ ( x - 1) ) + 1
=
01000
( 2)
( ( x ^ ( x - 1) ) + 1) / 2
=
00100
( 2)
Skoro umiemy wyznaczyć na jwiększą p ot ęgę dwójki dzielącą daną liczbę w czasie st ałym, t o
umiemy t eż zaimplement ować operację i nser t t ak, aby działała w czasie O(log n):
voi d i nser t ( i nt x, i nt v)
{
whi l e( x < N)
{
l oad[ x] += v;
x += ( ( x ^ ( x - 1) ) + 1) / 2;
}
}
J ak dot ąd udało nam się jedynie pogorszyć złożoność op eracji i nser t . Okazuje się jednak, że
dzięki poczynionym modyfikacjom uda nam się zredukować złożoność op eracji quer y do O(log N )!
Aby uprościć sobie t rochę implement ację, zauważmy, że zamiast pyt ać o sumaryczne ob ciążenie
na przedziale [a, b] wyst arczy, że p oznamy sumaryczne ob ciążenia na przedziałach [1, a − 1] i [1, b].
Ot o kod funkcji quer y wraz z p omocniczą funkcją sum:
i nt sum( i nt x)
{
i nt r es = 0;
whi l e( x > 0)
{
r es += l oad[ x] ;
x - = ( ( x ^ ( x - 1) ) + 1) / 2;
}
r et ur n r es;
}
i nt quer y( i nt a, i nt b)
{
r et ur n sum( b) - sum( a- 1) ;
}
> Struktury danych i ich za stosowania
< 27 >
8.2
D r zewa pr zedzi ał owe
Drzewo p ot ęgowe sprawdza się bardzo dobrze w przypadku gdy operacja i nser t dot yczy punk-
t ów. J eśli jednak musimy dodawać obciążenia na całe przedziały, pot rzebujemy st rukt ury nieco
bardziej rozbudowanej. J ako że zapyt anie o punkt możemy t rakt ować jak zapyt anie o przedział
długości 1, skupimy się od razu na na jogólniejszym przypadku, w kt órym wszyst kie operacje
dot yczą przedziałów.
R ozk ł ad na pr zedzi ał y bazowe
.
D e fi n icja 5. P r z e d zia ł e m b a zow y m nazywamy przedział o długości będącej pot ęgą
dwójki i począt ku w punkcie b ędącym wielokrot nością swojej długości.
Int eresuje nas rozkład danego przedziału na minimalną liczb ę rozłącznych przedziałów bazo-
wych, kt óre pokrywa ją dany przedział. Np. przedział [3, 9] ma rozkład na sumę przedziałów [3, 3],
[4, 7] i [8, 9].
Kluczowy t ut a j jest nast ępujący fakt :
Ć w iczen ie 19. Uzasadnij, że liczba przedziałów bazowych w rozkładzie jest rzędu
O(log k), gdzie k jest długością rozkładanego przedziału.
Tym razem nasze drzewo przedziałowe będzie pełnym drzewem binarnym, kt órego węzły od-
p owiadać będą przedziałom bazowym.
[0, 3]
[0, 1]
[2, 3]
[0, 0] [1, 1] [2, 2] [3, 3]
Obciążenia p oszczególnych przedziałów bazowych zapisywać b ędziemy w t ablicy l oad[ ] o roz-
miarze 2N , numerując węzły drzewa w nast ępujący sposób:
1
2
3
4
5
6
7
Drzewo z p owyższą numeracją węzłów ma nast ępujące własności:
•
ojcem węzła x jest x/ 2,
•
lewy syn węzła x ma indeks 2x a prawy 2x + 1,
•
węzły parzyst e są zawsze lewymi synami swoich ojców, nat omiast nieparzyst e prawymi,
•
drzewo przedziałowe o zakresie od 0 do N − 1 ma 2N − 1 węzłów a jego wysokość t o log N + 1.

< 28 >
Informatyka +
8.2.1
D r ze w o t y p u ( + ,+ )
Zacznijmy od omówienia st rukt ury udost ępnia jącej nast ępujące operacje:
•
i nser t ( a, b, v) — dodanie obciążenia v do punkt ów z przedziału [a, b]
•
quer y( a, b) — zsumowanie obciążeń punkt ów zawartych w przedziale [a, b]
J ak zrealizować met odę i nser t ? W iemy, że każdy przedział długości k można rozłożyć na
sumę O(log k) p odprzedziałów bazowych. W yst arczy więc, że zna jdziemy rozkład przedziału [a, b]
a nast ępnie dodamy wart ość v do każdego węzła drzewa odpowiada jącego podprzedziałowi z roz-
kładu. Aby uprościć implement ację, zaczniemy od znalezienia liści odp owiada jących przedziałom
[a, a] i [b, b], a nast ępnie, st art ując od nich, b ędziemy poruszać się w górę drzewa, uakt ualnia jąc
nap ot kane węzły odpowiada jące przedziałom zawartym w [a, b].
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4,5]
[6, 7]
[0, 0] [1, 1] [2,2] [3,3] [4, 4] [5, 5] [6,6] [7,7]
P rzedziały pogrubione t worzą rozkład przedziału [2, 7]. Wart o zauważyć, że nie zawsze ot rzy-
mamy rozkład na mi nimalną liczb ę p odprzedziałów. Łat wo jednak uzasadnić, że liczba odwiedzo-
nych węzłów będzie rzędu O(log N ).
J eżeli b ędziemy jednocześnie przechodzić ścieżkami od lewego i od prawego końca przedziału
t o nasze ścieżki w p ewnym momencie się spot ka ją (być może dopiero w korzeniu). J eśli nasze
ścieżki jeszcze się nie spot kały i w p ewnym momencie zna jdziemy się w węźle leżącym na prawej
ścieżce, kt óry jest prawym synem swojego ojca, t o kandydat em na przedział należący do szukanego
rozkładu jest brat obecnego węzła. Analogicznie w syt uacji gdy zna jdziemy się w węźle leżącym
na lewej ścieżce, kt óry jest lewym synem swojego ojca.
Czy t o wyst arczy aby móc zaimplement ować operację quer y? Niest et y nie, ponieważ może
się zdarzyć, że rozkłady dwóch zachodzących na siebie przedziałów nie będą mieć wsp ólnych
element ów.
Ć w ic zen ie 20. P oda j przykład t akich przedziałów.
Musimy zat em przechowywać w węzłach drzewa dodat kowe informacje. W dodat kowej t ablicy
sub[ x] pamięt ać będziemy sumę obciążeń wszystkich węzłów poddrzewa o korzeniu x, kt óre są
zapisane w t ym poddrzewie. P rzechodząc ścieżkami w górę drzewa musimy pamięt ać o akt ualizo-
waniu wart ości sub we wszyst kich nap ot kanych węzłach, korzyst a jąc z zależności rekurencyjnej:
sub[ x] = sub[ l ef t ( x) ] + sub[ r i ght ( x) ] + l oad[ x] * l engt h( x)
gdzie l ef t ( x) , r i ght ( x) t o pot omkowie węzła x, a l engt h( x) t o długość przedziału reprezent o-
wanego przez węzeł x.
Ot o kod funkcji i nser t :
voi d i nser t ( i nt a, i nt b, i nt v)
{
i nt l = N + a, r = N + b;
i nt l engt h = 1; / / dł ugość pr zedzi ał ów na akt ual ni e odwi edzanym pozi omi e
> Struktury danych i ich za stosowania
< 29 >
l oad[ l ] += v;
sub[ l ] += v;
/ / j eśl i a==b t o ni e dodaj emy obci ążeni a dwukr ot ni e
i f ( r ! = l )
{
l oad[ r ] += v;
sub[ r ] += v;
}
whi l e( l >= 1)
{
/ / j eśl i l i r ni e są sąsi adami w dr zewi e, t o spr awdzamy czy
/ / ni e t r zeba uakt ual ni ć węzł ów wewnęt r znych
i f ( l < r - 1)
{
i f ( l % 2 == 0) / / l j est l ewym synem swego oj ca
{
l oad[ l + 1] += v;
sub[ l + 1] += v * l engt h;
}
i f ( r % 2 == 1) / / r j est pr awym synem swego oj ca
{
l oad[ r - 1] += v;
sub[ r - 1] += v * l engt h;
}
}
/ / j eśl i l i r ni e są l i śćmi , t o uakt ual ni amy i ch war t ości sub
i f ( r < N)
{
sub[ l ] = sub[ 2 * l ] + sub[ 2 * l + 1] + l oad[ l ] * l engt h;
sub[ r ] = sub[ 2 * r ] + sub[ 2 * r + 1] + l oad[ r ] * l engt h;
}
/ / pr zechodzi my pozi om wyżej
l / = 2; r / = 2; l engt h * = 2;
}
}
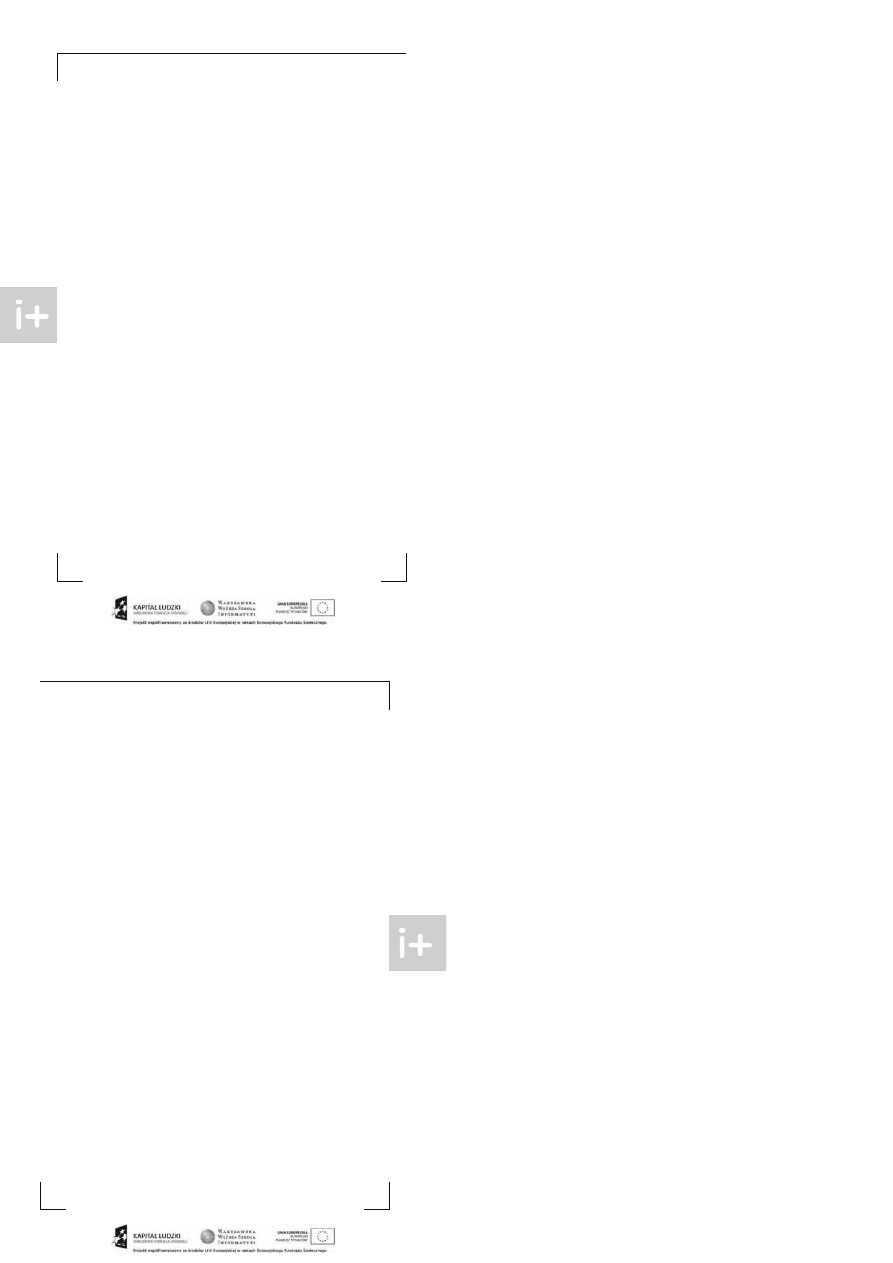
Implement acja funkcji quer y jest podobna:
i nt quer y( i nt a, i nt b)
{
i nt l = N + a, r = N + b;
i nt l engt h = 1; / / dł ugość pr zedzi ał ów na akt ual ni e odwi edzanym pozi omi e
/ / w l l en i r l en pami ęt amy i l e punkt ów pr zedzi ał u [ a, b] zawi er a
/ / si ę w poddr zewi e o kor zeni u l i r odpowi edni o
i nt l l en = 1, r l en = ( a ! = b ? 1 : 0) ;
i nt r es = 0;
whi l e( l >= 1)
{
< 30 >
Informatyka +
/ / sumuj emy obci ążeni a z węzł ów l i r
r es += l l en * l oad[ l ] + r l en * l oad[ r ] ;
/ / j eśl i l i r ni e są sąsi adami w dr zewi e t o spr awdzamy czy
/ / i st ni ej ą węzł y wewnęt r zne z obci ążeni em
i f ( l < r - 1)
{
i f ( l % 2 == 0) / / l j est l ewym synem swego oj ca
{
r es += sub[ l + 1] ;
l l en += l engt h;
}
i f ( r % 2 == 1) / / r j est pr awym synem swego oj ca
{
r es += sub[ r - 1] ;
r l en += l engt h;
}
}
/ / pr zechodzi my pozi om wyżej
l / = 2; r / = 2; l engt h * = 2;
}
r et ur n r es;
}
8.2.2
D r ze w o t y p u ( + ,m a x )
Drzewo t ypu (+ ,max) udost ępnia nast ępujące met ody:
•
i nser t ( a, b, v) — dodanie obciążenia v do punkt ów z przedziału [a, b]
•
quer y( a, b) — znalezienie maksymalnego obciążenia punkt u należącego do [a, b]
Konst rukcja drzewa jest niemal identyczna jak w przypadku (+ ,+ ), z t ym, że w t ablicy sub[ x]
będziemy przechowywać maksymalne obciążeni e wier zchoł ka z poddr zewa o korzeni u w x.
P oniżej zna jduje się kod met ody i nser t . Implement acja quer y jest niet rudnym ćwiczeniem.
voi d i nser t ( i nt a, i nt b, i nt v)
{
i nt l = N + a, r = N + b;
l oad[ l ] += v;
sub[ l ] += v;
/ / j eśl i a==b t o ni e dodaj emy obci ążeni a dwukr ot ni e
i f ( r ! = l )
{
l oad[ r ] += v;
sub[ r ] += v;
}
whi l e( l >= 1)
{
/ / j eśl i l i r ni e są sąsi adami w dr zewi e t o spr awdzamy czy
/ / ni e t r zeba uakt ual ni ć węzł ów wewnęt r znych
> Struktury danych i ich za stosowania
< 31 >
i f ( l < r - 1)
{
i f ( l % 2 == 0) / / l j est l ewym synem swego oj ca
{
l oad[ l + 1] += v;
sub[ l + 1] += v;
}
i f ( r % 2 == 1) / / r j est pr awym synem swego oj ca
{
l oad[ r - 1] += v;
sub[ r - 1] += v;
}
}
/ / j eśl i l i r ni e są l i śćmi t o uakt ual ni amy i ch war t ości sub
i f ( r < N)
{
sub[ l ] = max( sub[ 2 * l ] , sub[ 2 * l + 1] ) + l oad[ l ] ;
sub[ r ] = max( sub[ 2 * r ] , sub[ 2 * r + 1] ) + l oad[ r ] ;
}
/ / pr zechodzi my pozi om wyżej
l / = 2; r / = 2;
}
}
8.2.3
D r ze wo t y p u ( m a x ,m a x )
Tym razem nasze drzewo udost ępnia nast ępujące met ody:
•
i nser t ( a, b, v) — dla każdego punkt u x należącego do przedziału [a, b] wykonanie p odst a-
wienia l oad[ x] = max( l oad[ x] , v)
•
quer y( a, b) — znalezienie maksymalnego ob ciążenia punkt u należącego do [a, b]
Implement acja nieznacznie różni się od implement acji drzewa (+ ,max) — pozost awiamy ją
jako ćwiczenie.
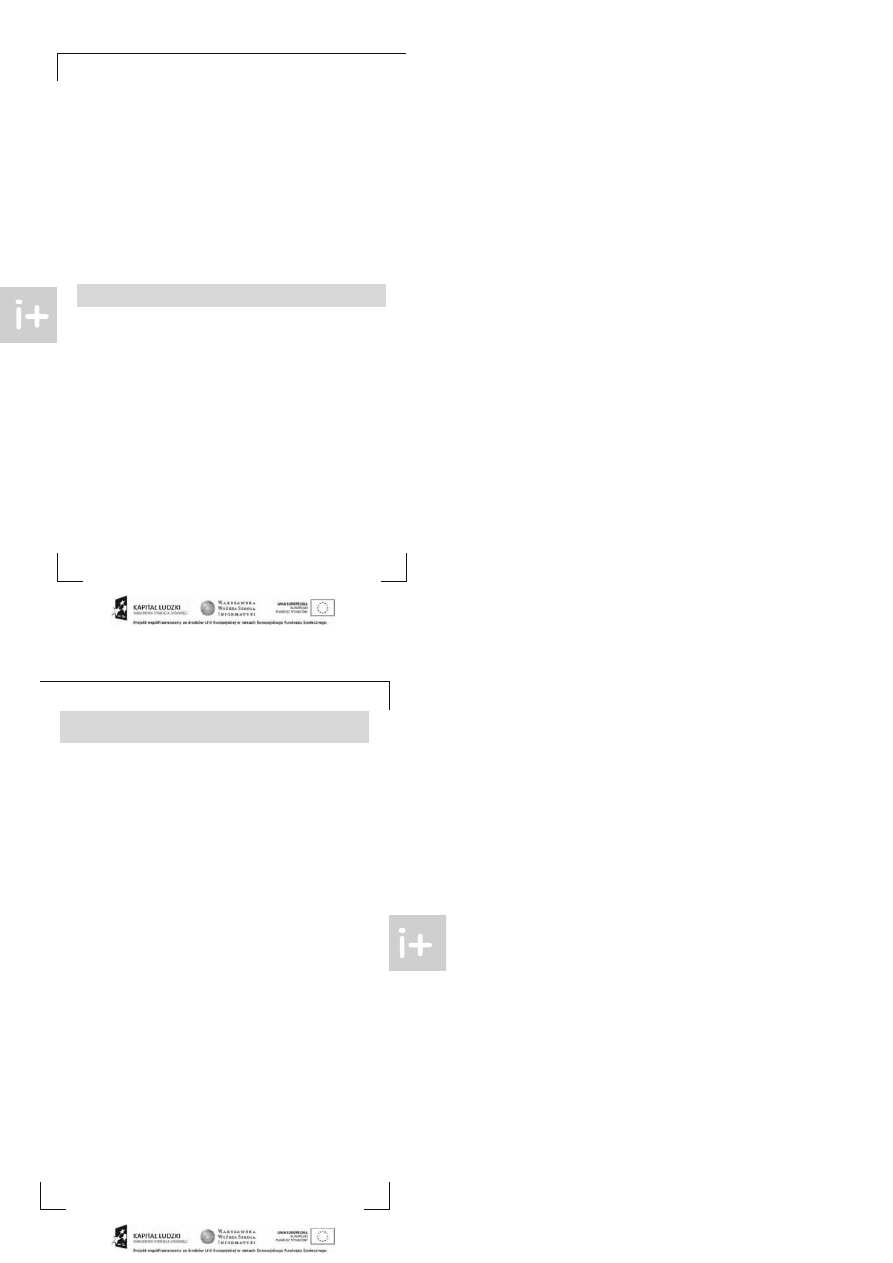
Zadani a
1. Zaimplement uj rekurencyjne odp owiedniki met od i nser t i quer y dla dowolnego z oma-
wianych drzew przedziałowych. P orówna j czasy działania obu wersji dla dużych danych
wejściowych.
2. J eżeli x jest zmienną typu i nt , t o wyrażenie ( ( x ^ ( x - 1) ) + 1) / 2 możemy zast ą pić
przez ( x & - x) . Up ewnij się, że rozumiesz dlaczego wyrażenia t e zwraca ją t ę samą wart ość.
3. Do kt órych drzew można wst awiać za p omocą i nser t wart ości ujemne? Kt óre wymaga ją
modyfikacji?
4. Zadanie K oleje z IX Olimpiady Informatycznej (dost ępne w [5]).
< 32 >
Informatyka +
9
Techni ka zam iat ani a
W pr owadzenie
Technika zamiat ania jest jednym z p odst awowych p odejść do rozwiązywania problemów geome-
t rycznych. Na t ych za jęciach pokażemy przykłady kilku problemów, kt óre można rozwiązać t ym
sposobem.
Aby przeprowadzić zamiat anie pot rzebujemy m iot ł y . Zwykle jest t o prost a, kt óra przesuwa się
nad całą płaszczyzną i przegląda kolejno napotykane obiekt y (np. punkt y, czy t eż figury). Umówmy
się na pot rzeby t ych not at ek, że miot ła jest pionowa i przesuwa się od lewej do prawej, czyli
zgodnie ze wzrost em współrzędnej x. W miarę nap otykania kolejnych obiekt ów miot ła zapamięt uje
informacje pot rzebne do rozwiązania problemu. W typowym przypadku wykorzyst uje do t ego
st rukt urę danych t aką, jak na przykład drzewo przedziałowe, o kt órym mówiliśmy na p oprzednich
za jęciach.
Par y pr zecinaj ący ch si ę odcinków
Zamiat anie na jlepiej pokazać na konkret nym przykładzie:
Na płaszczyźnie zna jduje się n pionowych i p oziomych odcinków. Chcemy policzyć
wszyst kie przecięcia odcinków pionowych z poziomymi.
Zadanie t o rozwiązać można prost ym algoryt mem w czasie O(n
2
) — wyst arczy dla każdej pary
prost opadłych odcinków stwierdzić, czy przecina ją się ze sobą.
Ć w ic zen ie 21. J ak sprawdzałbyś, czy dwa odcinki są prost opadłe? J ak można użyć w
t ym celu iloczynu skalarnego wekt orów?
My jednak pokażemy znacznie szybsze rozwiązanie, kt óre działa w czasie O(n log n), opart e
na t echnice zamiat ania. Nasza miot ła, czyli pionowa prost a przesuwa jąca się w prawo, b ędzie się
zat rzymywać, gdy napot ka jedno z nast ępujących zd a r ze ń :
•
p ocząt ek poziomego odcinka,
•
koniec poziomego odcinka,
•
odcinek pionowy.
Chcemy, by w każdym momencie swojej wędrówki miot ła znała odcinki poziome, kt óre się
pod nią zna jdują (przecina ją się z nią). W rzeczywist ości wyst arczy przechowywać współrzędne
igrekowe t ych odcinków. W t ym celu, gdy miot ła nap ot ka począt ek p oziomego odcinka, musi
zapamięt ać jego współrzędne, aż do moment u osią gnięcia jego końca.
W momencie, gdy pod miot łą pojawi się odcinek pionowy, będziemy zliczali ile odcinków
poziomych się z nim przecina. Załóżmy, że wsp ółrzędne igrekowe jego dolnego i górnego końca t o
odpowiednio y
1
i y
2
. Zapyt amy więc miot łę ile odcinków p oziomych, kt óre akt ualnie zna jdują się w
miot le, ma współrzędne z przedziału [y
1
, y
2
]. P o zsumowaniu wyników dla wszyst kich nap ot kanych
pionowych odcinków ot rzymamy ost at eczny rezult at .
P ozost a je jeszcze powiedzieć, jak zrealizować miot łę, by można było szybko dodawać i usuwać
wsp ółrzędne odcinków, a t akże zliczać współrzędne z określonych przedziałów. W ykorzyst amy
w t ym celu drzewo pot ęgowe! Każdy jego punkt będzie reprezent ował jedną współrzędną igre-
kową, zaś obciążeniem punkt u jest liczba odcinków, kt óre są akt ualnie p od miot łą na t ej wsp ół-
rzędnej. Op eracje, kt óre wykonuje miot ła odp owiada ją dokładnie op eracjom udost ępnianym przez
drzewo pot ęgowe — dokonuje ona zmiany obciążenia w danym punkcie oraz sumowania ob ciążeń
z określonego przedziału.
P rzyjrzyjmy się jeszcze raz st rukt urze całego rozwiązania. Na począt ku musimy stworzyć i po-
sort ować po pierwszej współrzędnej wszyst kie zdarzenia, kt óre napot ka miot ła. Można t o zrobić
> Struktury danych i ich za stosowania
< 33 >
w czasie O(n log n). P óźniej, każde zdarzenie obsługujemy w czasie O(log n). W t en sp osób udało
nam się rozwiązać pierwszy problem, t ak jak obiecywaliśmy, w czasie O(n log n).
Ć w iczen ie 22. Co należy zrobić gdy nie można po prost u zast osować drzewa p ot ę-
gowego, gdyż przedział, w jakim zna jdują się współrzędne końców odcinków jest zbyt
duży?
I m pl ement acj a
Na począt ku napiszmy st rukt urę opisującą zdarzenie.
st r uct event
{
i nt x; / * współ r zędna, na kt ór ej wyst ępuj e zdar zeni e * /
/ * Typ zdar zeni a:
*
/ *
1 - począt ek odci nka pozi omego
*
* - 1 - koni ec odci nka pozi omego
*
*
0 - odci nek pi onowy
* /
i nt t ype;
i nt y1, y2; / * dol na i gór na współ r zędna y
*
* ( dl a odci nków pozi omych y1 = y2) * /
i nt oper at or <( const event & e) const
{
i f ( x == e. x)
r et ur n t ype > e. t ype;
el se
r et ur n x < e. x;
}
} ;
Funkcja oper at or < definiuje op e r a t or p or ów n u ją cy obiekt y danej st rukt ury. P owinna ona
zwracać wart ość t r ue wt edy i t ylko wt edy, gdy obiekt lokalny jest mniejszy od obiekt u przesłanego
jako paramet r. Dzięki niej możemy porównywać dwie zmienne typu event jak zwykłe liczby. Gdy
mamy zdefiniowany t aki operat or, możemy t eż posort ować t ablicę, lub wekt or obiekt ów klasy
event przez wywołanie funkcji sor t z bibliot eki ST L.
W wyniku t ego sort owania chcemy mieć zdarzenia ułożone w kolejności, w jakiej ma je nap o-
t ykać miot ła. Dlat ego op erat or t en porządkuje zdarzenia w pierwszej kolejności p o współrzędnej
x, a w przypadku remisu porównuje również typy zdarzeń. Kolejność, w jakiej należy przetwarzać
zdarzenia o t ej samej pierwszej współrzędnej, należy dokładnie przemyśleć. W yobraźmy sobie, że
na p ewnej współrzędnej x zachodzą zdarzenia wszyst kich t rzech t ypów: jeden odcinek poziomy się
rozp oczyna, inny się kończy, a pewien odcinek pionowy dotyka obydwóch odcinków poziomych.
Sprawdzenie, ilu odcinków p oziomych dot yka t en pionowy t rzeba więc wykonać po wst awieniu
odcinków, kt óre zaczyna ją się na danej wsp ółrzędnej, ale przed usunięciem tych, kt óre właśnie się
kończą. St ąd, poszczególne typy zdarzeń, w ramach t ej samej pierwszej wsp ółrzędnej, są sort owane
właśnie w t ej kolejności. P amięt a j, że za każdym razem gdy projekt ujemy algoryt m używa jący
t echniki zamiat ania, t rzeba zast anowić się w jakiej kolejności należy przeglądać zdarzenia o t ej
samej pierwszej wsp ółrzędnej. Czasami odp owiednia kolejność jest jednoznacznie wyznaczona (jak
w powyższym przykładzie), ale zdarza się t eż, że p ewne obliczenia chcemy wykonać dopiero po
obsłużeniu wszyst kich zdarzeń na danej wsp ółrzędnej.
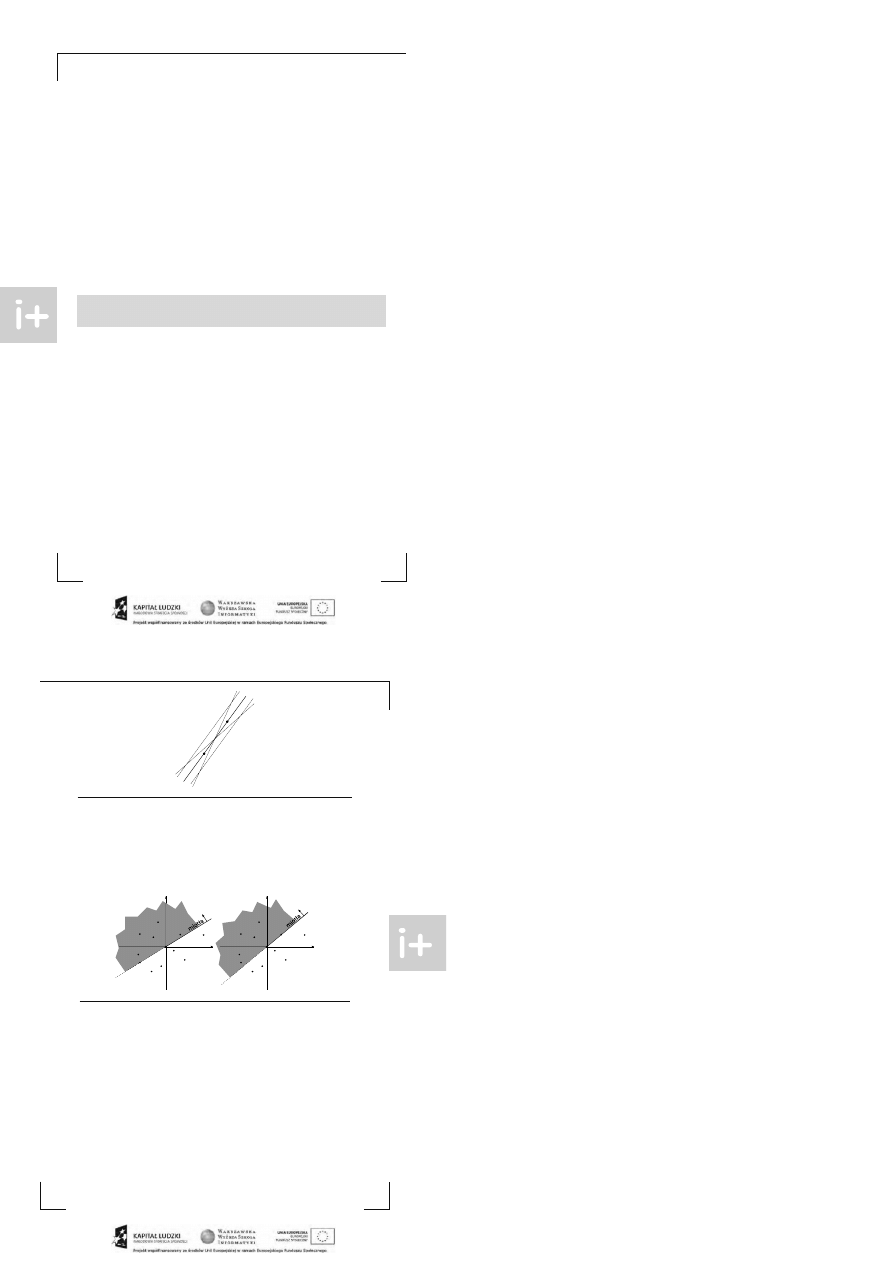
P rzejdźmy t eraz do kodu realizującego zamiat anie:
/ / event s - kont ener t ypu vect or <event > pr zechowuj ący zdar zeni a
/ / sor t uj emy zdar zeni a zgodni e ze zdef i ni owanym por ządki em
sor t ( event s. begi n( ) , event s. end( ) ) ;
< 34 >
Informatyka +
/ / zmi enna zl i czaj ąca znal ezi one pr zeci ęci a
l ong l ong i nt er = 0;
f or ( i nt i =0; i <( i nt ) event s. si ze( ) ; i ++)
{
i f ( event s[ i ] . t ype == 0) / / odci nek pi onowy
i nt er += quer y( event s[ i ] . y1, event s[ i ] . y2) ;
el se
i nser t ( event s[ i ] . y1, event s[ i ] . t ype) ;
}
Korzyst amy z drzewa pot ęgowego, omawianego na poprzednich za jęciach. P rzypomnijmy, że
i nser t ( x, v) doda je ob ciążenie v do punkt u x, zaś quer y( a, b) zwraca sumę obciążeń na prze-
dziale [a, b].
Co j eszcze p ot r afi zam iat anie?
Wachlarz problemów, kt óre p ot rafimy rozwiązać przez zamiat anie, zależy w dużej mierze od zna-
nych nam st rukt ur danych. Na przykład, korzyst a jąc z drzewa przedziałowego t ypu (+ , max),
rozwiązać możemy nast ępujący problem: na płaszczyźnie zna jdują się prost okąt y o bokach rów-
noległych do osi układu współrzędnych; zna jdź punkt , kt óry jest przykryt y na jwiększą liczbą
prost okąt ów.
J ako zdarzenia rozpat rujemy t u lewe i prawe b oki prost okąt a, a miot ła pamięt a, ile prost okąt ów
zna jduje się pod nią na każdej wsp ółrzędnej. Gdy nap ot ykamy lewy b ok prost okąt a doda jemy je-
dynkę na przedziale wyznaczonym przez wsp ółrzędne igrekowe jego poziomych boków. P o każdym
dodaniu prost okąt a, szukamy punkt u w miot le, kt óry jest przykryt y na jwiększą liczbą prost okąt ów.
Ć w ic zen ie 23. W t ym problemie t eż należy uważać na syt uację, w kt órej wiele zdarzeń
ma t ą samą pierwszą współrzędną. W jakiej kolejności należy je przeglądać, by algoryt m
działał poprawnie?
9.1
Zam iat ani e kąt owe
Za jmiemy się t eraz t rochę innym sp osob em przeglądania obiekt ów na płaszczyźnie. Nie ma on
dobrze rozpowszechnionej nazwy, jednak z p owodu pewnych podobieńst w do zamiat ania, b ędziemy
go nazywać za m ia t a n ie m ką t ow y m .
W t ym przypadku, miot ła jest półprost ą zaczepioną w ust alonym punkcie. P ółprost a t a prze-
gląda płaszczyznę wykonując obrót o 360
◦
. T ym razem umówmy się, że p ółprost a obracać się
będzie przeciwnie do ruchu wskazówek zegara. Rozważmy nast ępujący przykładowy problem:
Na płaszczyźnie zna jduje się n punkt ów, sp ośród kt órych żadne t rzy nie leżą na jednej
prost ej. Z każdym punkt em skojarzona jest waga, określona dodat nią liczbą całkowit ą.
Chcemy narysować na płaszczyźnie prost ą, t ak, by sumy wag punkt ów p o obydwóch
st ronach prost ej były sobie jak na jbliższe.
Zast anówmy się na jpierw jak napisać rozwiązanie, kt óre rozpat rzy wszyst kie możliwe prost e.
P o pierwsze, zauważmy, że możemy ograniczyć się do rozważania t akich prost ych, kt óre przechodzą
przez dokładnie dwa punkt y. Nawet jeśli pewna opt ymalna prost a nie przechodzi przez żaden
punkt , możemy ją t ak przesunąć i obrócić, by oparła się na dwóch punkt ach.
Z drugiej st rony, ponieważ nie ma t rzech punkt ów współliniowych, jeśli mamy prost ą przecho-
dzącą przez dwa punkty, t o możemy ją minimalnie przesunąć lub obrócić, t ak by każdy z tych
dwóch punkt ów znalazł się po jednej lub drugiej st ronie prost ej (pat rz rysunek).
Rozwiązanie naszego problemu wygląda zat em t ak: dla każdej pary punkt ów (t akich par jest
O(n
2
)) prowadzimy przez nie prost ą, liczymy sumy wag punkt ów po jednej i drugiej st ronie (w cza-
sie O(n)) a nast ępnie rozpat rujemy 4 możliwości przydzielenia punkt ów z prost ej do jednej lub
drugiej części płaszczyzny. W t en sp osób dost a jemy algoryt m w złożoności O(n
3
).
> Struktury danych i ich za stosowania
< 35 >
Rys. 1: Pr ost a pr zechodząca przez dwa punkt y i czt er y możliwości jej przesunięcia i obr ot u
Korzyst a jąc z zamiat ania kąt owego poprawimy czas działania do O(n
2
log n). Dla każdego
punkt u z płaszczyzny, b ędziemy wykonywali dookoła niego zamiat anie kąt owe. Chcemy w każdym
momencie wykonania algoryt mu znać sumę wag punkt ów na p ółpłaszczyźnie p o lewej st ronie
miot ły (t j. po st ronie przeciwnej do ruchu wskazówek zegara). Gdy miot ła napot ka punkt , należy
go z miot ły usunąć. J eśli zaś punkt zna jdzie się na przedłużeniu miot ły, jest on do niej dodawany.
Syt uację wyjaśnia ją rysunki.
Rys. 2: M oment dodania punkt u do miot ł y ( po lewej) oraz usunięcia punkt u (po prawej) .
W momencie, gdy napotykamy punkt , sprawdzamy czt ery możliwości narysowania prost ej,
odp owiada jące możliwościom przydzielenia punkt ów do jednej z dwóch p ółpłaszczyzn. Można
sobie zaoszczędzić nieco pracy i zauważyć, że wyst arczy sprawdzać jedynie dwie op cje: punkt
wokół kt órego zamiat amy przydzielamy do jednej lub drugiej st rony płaszczyzny. W t en sposób
również rozważymy wszyst kie dost ępne podziały płaszczyzny.
9.2
Sor t owanie kąt owe
Implement ację zamiat ania kąt owego p ozost awiamy jako ćwiczenie, op owiemy jedynie pokrót ce, jak
w prosty sp osób posort ować punkty kąt owo. Z pomocą przychodzi nam funkcja at an2 z bibliot eki
st andardowej C+ + .
doubl e at an2( doubl e y, doubl e x) ;
Tak, t o nie pomyłka, pierwszym argument em t ej funkcji jest wsp ółrzędna y, zaś drugim — współ-
rzędna x. Funkcja t a zwraca kąt , jaki t worzy odcinek łączący punkt (x, y) z dodat nią półosią
X wyrażony w radianach (zwracana wart ość jest liczbą z przedziału [− π, π]). J eżeli zamiast na

< 36 >
Informatyka +
radianach, wolimy operować na st opniach z przedziału [− 180, 180] t o możemy ot rzymaną war-
t ość p omnożyć przez
180
π
. Aby użyć funkcji at an2, należy do programu dołączyć plik nagłówkowy
cmat h.
Trzeba być jednak ost rożnym używa jąc funkcji at an2, p onieważ zapisuje ona wynik w liczbie
zmiennoprzecinkowej (pamięt anej w komput erze z ograniczoną dokładnością). J eśli kąty wyzna-
czone przez dwa punkt y różnią się bardzo nieznacznie, at an2 może zwrócić dla nich t ę samą
wart ość. Zwykle uważa się, że jeżeli współrzędne punkt ów ma ją wart ości b ezwzględne większe niż
10
6
, b ezpieczniej jest użyć funkcji
l ong doubl e at an2l ( l ong doubl e y, l ong doubl e x) ;
i zmiennych t ypu l ong doubl e. J eśli współrzędne mogą być większe niż 10
9
, nawet wyniki at an2l
mogą być niewyst arcza jąco dokładne.
Ć w ic zen ie 24. Ambi tne: J ak wykorzyst ać iloczyn wekt orowy do kąt owego sort owania?
Czy t eż t rzeba się wt edy mart wic o dokładność wyniku?
Zadania
1. Zadanie Wyspy z XI Olimpiady Informat ycznej (dost ępne w [5]).
2. Na płaszczyźnie zamalowujemy na czarno wnęt rza n prost okąt ów o bokach równoległych
do osi układu współrzędnych. J akie jest pole zamalowanej części płaszczyzny?
3. Zaimplement uj rozwiązanie zadania z rozdziału o zamiat aniu kąt owym.
4. Na płaszczyźnie dane są punkt y. Zna jdź t akie t rzy spośród nich, kt óre t worzą kąt o jak
na jwiększej mierze.
10
D r zewa T R I E
P r oblem
Wiemy już, że za pomocą algoryt mu KMP jest eśmy w st anie znaleźć wszyst kie wyst ą pienia wzorca
w t ekście w czasie liniowym. P roblem wyszukiwania wzorca można nieco uogólnić i zapyt ać jak
szybko jest eśmy w st anie znaleźć wszyst kie wyst ą pienia wielu wzorców w zadanym t ekście.
Możemy użyć algoryt mu KMP do każdego wzorca z osobna a nast ępnie scalić wyniki. J eżeli
wszyst kich wzorców jest n a t ekst ma długość m t o rozwiązanie t o ma złożoność O(n ·m). Algoryt m
Aho-Corasick p ozwala znacznie polepszyć t en wynik.
D r zewo T R I E
Będziemy korzyst ali ze st rukt ury danych o nazwie T RIE. J est t o drzewo ukorzenione, kt órego
krawędzie są et ykiet owane symbolami danego alfab et u. W dalszej części b ędziemy zakładali, że
nasz alfab et t o zbiór lit er alfabet u angielskiego.
Drzewo T RIE reprezent uje p ewien zbiór słów nad ust alonym alfabet em. Inaczej niż w do-
tychczas omawianych drzewach, elementy zbioru nie są przechowywane w węzłach lecz można je
odt worzyć na p odst awie p ozycji węzłów w drzewie. Słowo reprezent owane przez węzeł x ot rzy-
mamy przechodząc po ścieżce od korzenia do x i odczyt ując lit ery na kolejnych krawędziach. Nie
wszyst kie węzły b ędą reprezent ować elementy zna jdujący się w zbiorze, dlat ego w każdym węźle
przechowujemy dodat kowo wart ość logiczną, wskazującą czy węzeł t en odpowiada ist niejącemu
element owi.
> Struktury danych i ich za stosowania
< 37 >
⊥
◦
•
•
•
◦
◦
•
•
a
a
b
c
c
a
b
a
Na rysunku powyżej zamalowane węzły odp owiada ją słowom przechowywanym w drzewie.
Korzeń (oznaczony symb olem ⊥) odp owiada słowu pust emu. P owyższe drzewo reprezent uje zbiór
słów {„aa”, „ab”, „abc”, „caa”, „cb”}, nat omiast słowa „a”, „c” czy „ca” t o t ego zbioru nie należą.
Drzewo T RIE udost ępniać będzie nast ępujące met ody:
•
inser t — wst awienie słowa do zbioru,
•
search — sprawdzenie, czy słowo należy do zbioru,
•
erase — usunięcie słowa ze zbioru.
W każdym węźle musimy przechowywać zbiór wskaźników do pot omków. J eśli nasz alfab et
nie jest zbyt duży (a na jczęściej b ędzie t o alfab et angielski, czyli 26 lit er) możemy p okusić się
o dodanie do każdego węzła 26-element owej t ablicy wskaźników, co nieco uprości implement a-
cję. W iąże się t o jednak z t rochę większym narzut em pamięciowym oraz koniecznością zerowania
t ablic w konst rukt orze. Alt ernat ywnym p odejściem jest zast osowanie kont enera map z bibliot eki
ST L, w kt órym przechowywane są pary (lit era, odpowiada jący jej wskaźnik do pot omka). Aby nie
komplikować nadmiernie implement acji, zast osujemy pierwszą met odę.
Ot o (niep ełna) implement acja drzewa T RIE:
#def i ne ALPH 26
/ / r ozmi ar al f abet u
st r uct Tr i eNode
/ / węzeł dr zewa TRI E
{
/ / konst r ukt or ust awi aj ący oj ca i znak na kr awędzi pr owadzącej od oj ca
Tr i eNode( Tr i eNode * _par ent , char _l ast )
{
f or ( i nt i = 0; i < ALPH; ++i )
l i nks[ i ] = NULL;
par ent = _par ent ;
l ast = _l ast ;
i n_di ct = f al se;
}
Tr i eNode * l i nks[ ALPH] ;
/ / t abl i ca pot omków
Tr i eNode * par ent ;
/ / wskaźni k do oj ca
char l ast ;
/ / znak na kr awędzi pr owadzącej od oj ca
bool i n_di ct ;
/ / czy sł owo j est w dr zewi e
} ;
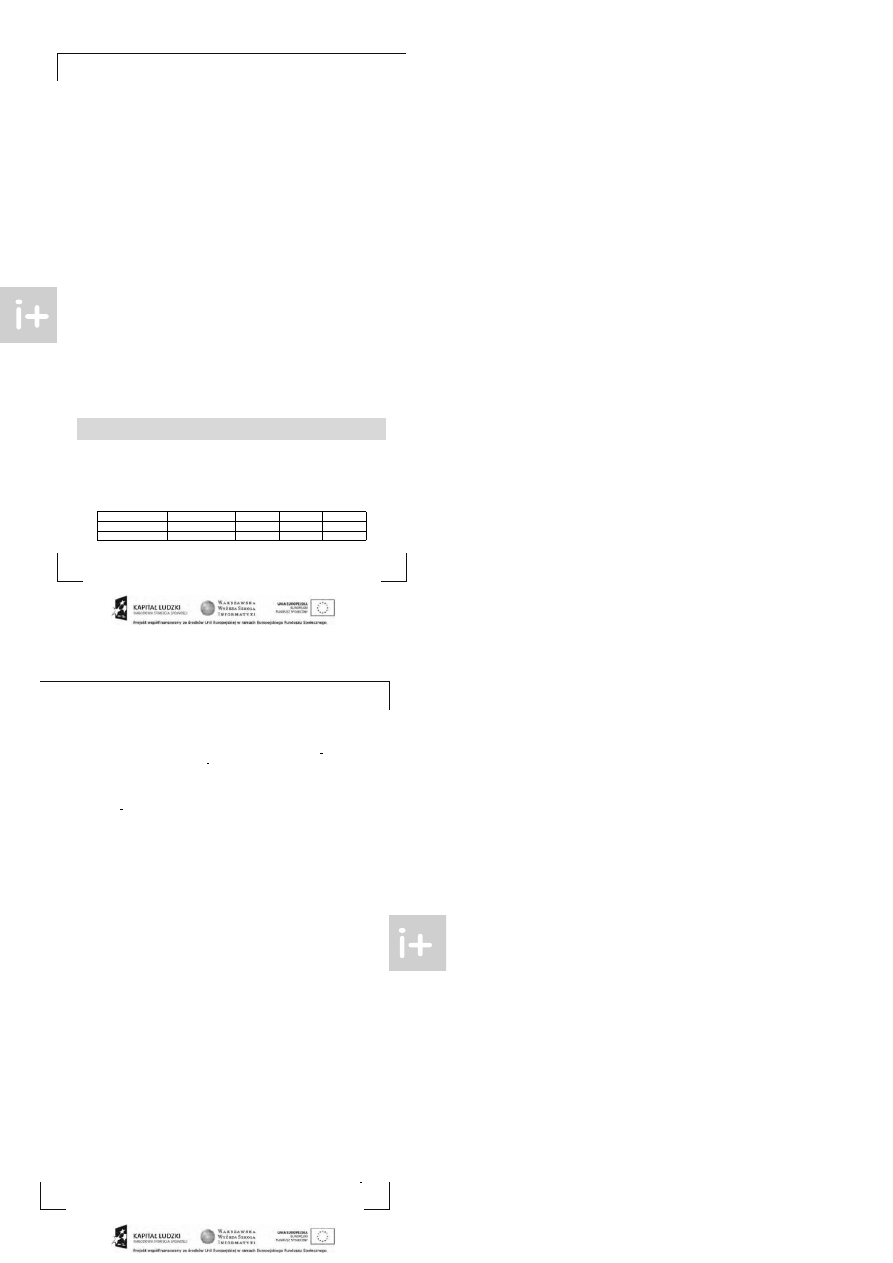
< 38 >
Informatyka +
st r uct Tr i e
{
Tr i e( )
/ / konst r ukt or t wor zący kor zeń dr zewa
{
r oot = new Tr i eNode( NULL, ’ - ’ ) ;
}
voi d i nser t ( st r i ng &wor d)
{
Tr i eNode * v = r oot ;
/ / wskaźni k na akt ual ny węzeł
f or ( i nt i = 0; i < ( i nt ) wor d. si ze( ) ; ++i )
{
i f ( v- >l i nks[ wor d[ i ] - ’ a’ ] == NULL)
/ / j eśl i ni e ma j eszcze kr awędzi z daną l i t er ą
/ / t o ut wór z nowego pot omka
v- >l i nks[ wor d[ i ] - ’ a’ ] = new Tr i eNode( v, wor d[ i ] ) ;
v = v- >l i nks[ wor d[ i ] - ’ a’ ] ;
}
v- >i n_di ct = t r ue;
}
bool sear ch( st r i ng &wor d)
{
Tr i eNode * v = r oot ;
/ / wskaźni k na akt ual ny węzeł
f or ( i nt i = 0; i < ( i nt ) wor d. si ze( ) ; ++i )
{
i f ( v- >l i nks[ wor d[ i ] - ’ a’ ] == NULL)
/ / j eśl i ni e ma kr awędzi z daną l i t er ą t o zwr óć f ał sz
r et ur n f al se;
el se
/ / j eśl i j est t o pr zej dź po ni ej
v = v- >l i nks[ wor d[ i ] - ’ a’ ] ;
}
r et ur n v- >i n_di ct ;
}
Tr i eNode * r oot ;
} ;
Ć w ic zen ie 25. Uzup ełnij powyższą implement ację o brakującą met odę er ase oraz
dest rukt ory zwalnia jące zaalokowaną pamięć.
P rzy założeniu, że nasz alfab et jest 26-element owy, możemy przyjąć, że wszyst kie operacje na
zbiorze l i nks wykonywane są w czasie st ałym. P rzy t akim założeniu, złożoność wszyst kich op era-
cji na drzewie T RIE jest liniowa względem długości wst awianego (lub usuwanego czy szukanego)
słowa.
J eżeli nasz alfab et byłby duży i miał rozmiar k t o złożoności p oszczególnych operacji na słowie
o długości n zależałyby od implement acji:
ut worzenie węzła
insert
search
erase
T RIE z mapami
O(1)
O(n log k)
O(n log k)
O(n log k)
T RIE z t ablicami
O(k)
O(n · k)
O(n)
O(n)
> Struktury danych i ich za stosowania
< 39 >
11
A l gor yt m A ho-Cor asi ck
Działanie algoryt mu Aho-Corasick (w skrócie AC) jest analogiczne do algoryt mu KMP. Dlat ego
t eż pot rzebować będziemy odp owiednika t ablicy prefiksowej w post aci drzewa T RIE, do kt órego
począt kowo wst awimy wszyst kie wzorce.
W każdym węźle naszego drzewa chcemy pamięt ać dodat kową wart ość suf l i nk. J eśli węzeł
x reprezentuje słowo s to chcemy aby x. suf l i nk był wskaźnikiem do węzła reprezent ującego
na jdłuższy właściwy sufiks słowa s, kt óry jest jednocześnie prefiksem pewnego wzorca. Różnica
względem algoryt mu KMP jest t aka, że sufiks t en nie musi być prefiksem t ego samego wzorca (nie
musi być jego prefikso-sufiksem).
Wart ości p ól suf l i nk obliczymy podobnie jak w algoryt mie KMP, przy czym drzewo prze-
chodzić będziemy algoryt mem BF S (można t ut a j równie dobrze użyć algoryt mu DF S):
voi d cr eat e_l i nks( Tr i e &t r i e)
{
/ / pr zechodzi my dr zewo al gor yt mem BFS
queue<Tr i eNode* > Q;
/ / wst awi amy kor zeń do kol ej ki
Q. push( t r i e. r oot ) ;
t r i e. r oot - >suf _l i nk = t r i e. r oot - >di ct _l i nk = NULL;
whi l e( ! Q. empt y( ) )
{
Tr i eNode * v = Q. f r ont ( ) ;
Q. pop( ) ;
i f ( v ! = t r i e. r oot )
/ / węzeł ni e j est kor zeni em
{
/ / post ępuj emy t ak j ak w KMP - cof amy si ę po kol ej nych suf _l i nkach
/ / dopóki ni e nat r af i my na kr awędź o odpowi edni ej et yki eci e
Tr i eNode * j = v- >par ent - >suf _l i nk;
whi l e( j && j - >l i nks[ v- >l ast - ’ a’ ] == NULL)
j = j - >suf _l i nk;
i f ( j == NULL)
v- >suf _l i nk = t r i e. r oot ;
el se v- >suf _l i nk = j - >l i nks[ v- >l ast - ’ a’ ] ;
i f ( v- >suf _l i nk- >i n_di ct )
/ / ust awi amy di ct _l i nk
v- >di ct _l i nk = v- >suf _l i nk;
el se v- >di ct _l i nk = v- >suf _l i nk- >di ct _l i nk;
}
/ / wst awi amy wszyst ki ch pot omków v do kol ej ki
f or ( i nt i = 0; i < ALPH; ++i )
i f ( v- >l i nks[ i ] ! = NULL)
Q. push( v- >l i nks[ i ] ) ;
}
}
W p owyższym kodzie, dla każdego węzła v ust awiana jest dodat kowo wart ość v- >di ct l i nk,
kt óra jest wskaźnikiem do na jdłuższego właściwego sufiksu węzła v, kt óry jest jednym z wzorców.
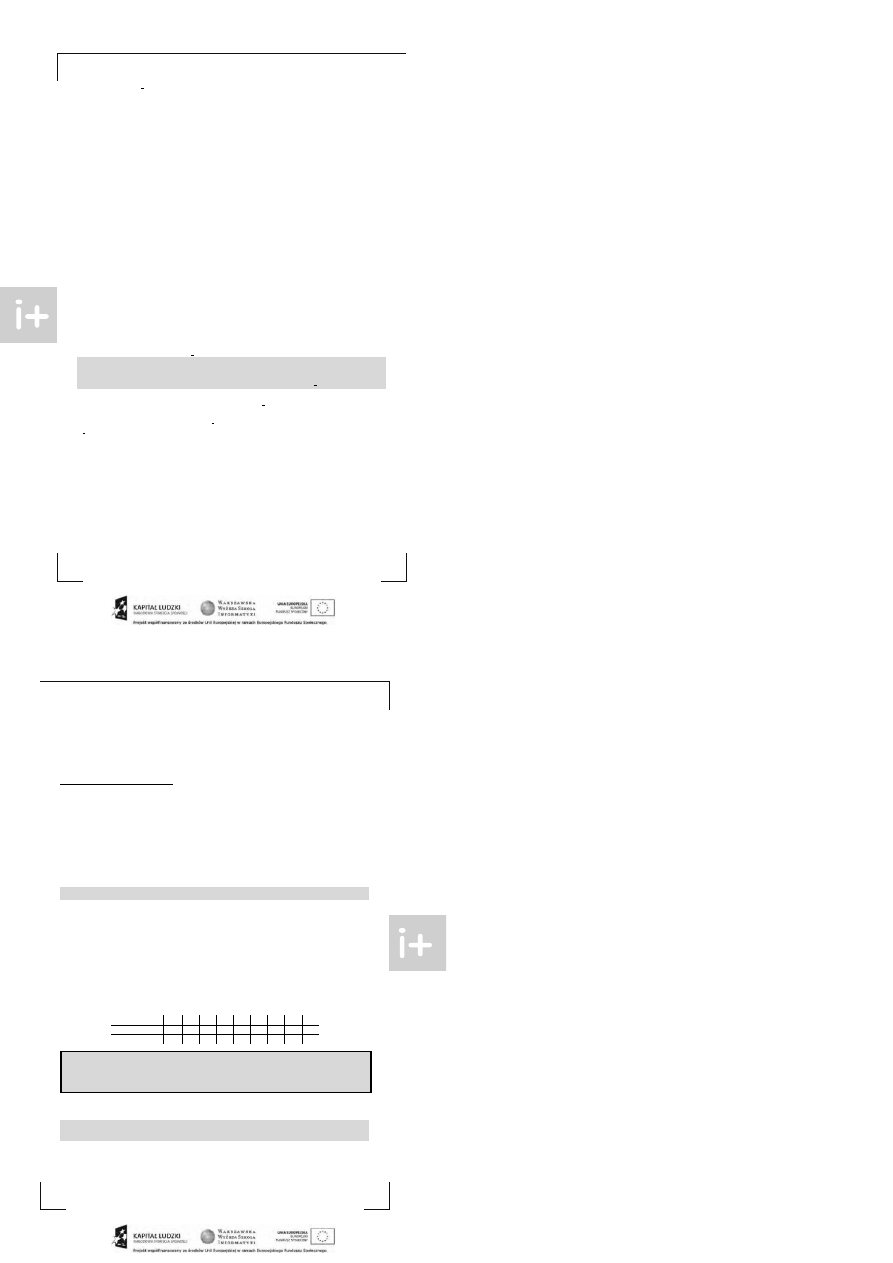
< 40 >
Informatyka +
Może się bowiem zdarzyć, że w jednym miejscu t ekst u kończy się kilka dopasowań wzorców (na
przykład wyszukiwanie wzorców ze zbioru {„abc”, „bc”, „c”} w t ekście „ab cd”). W t akim przy-
padku, wskaźnik di ct l i nk będzie pot rzebny do odt worzenia wszyst kich dopasowanych wzorców.
Zasada działania algoryt mu AC jest t aka, jak algoryt mu KMP :
voi d aho_cor asi ck( Tr i e &t r i e, st r i ng &t ext )
{
Tr i eNode * v = t r i e. r oot , * t mp;
f or ( i nt i = 0; i < ( i nt ) t ext . si ze( ) ; ++i )
{
whi l e( v && v- >l i nks[ t ext [ i ] - ’ a’ ] == NULL)
v = v- >suf _l i nk;
i f ( v == NULL)
v = t r i e. r oot ;
el se v = v- >l i nks[ t ext [ i ] - ’ a’ ] ;
/ / spr awdzamy, czy są j aki eś dopasowani a
i f ( v- >i n_di ct )
t mp = v;
el se t mp = v- >di ct _l i nk;
whi l e( t mp)
{
pr i nt f ( " Znal ezi ono wyst api eni e wzor ca numer %d. \ n" , t mp- >i d) ;
t mp = t mp- >di ct _l i nk;
}
}
}
J eżeli p o przet worzeniu kolejnej lit ery z t ekst u zna jdziemy się w węźle drzewa T RIE różnym
od korzenia, musimy sprawdzić, czy t en węzeł nie reprezent uje wzorca, a t akże wypisać wszyst kie
dopasowania osią galne poprzez di ct l i nk.
Ć w ic zen ie 26. Ważnym przypadkiem szczególnym jest syt uacja, w kt órej wszyst kie
wzorce są jednakowej długości. Zakłada jąc, że t akie właśnie są dane wejściowe, zaimple-
ment uj alt ernatywną wersję algoryt mu AC, nie korzyst a jącą z di ct l i nków.
J aką złożoność ma algoryt m Aho-Corasick? Wst awienie wzorców do drzewa odbywa się w cza-
sie liniowym względem sumy ich długości. Funkcja cr eat e l i nks również działa w czasie liniowym
względem sumy długości wzorców, co można uzasadnić analogicznie jak w oszacowaniu złożono-
ści algoryt mu KMP. Wreszcie funkcja aho cor asi ck, kt óra, pomija jąc przeglądanie wskaźników
di ct l i nk, działa liniowo względem sumy długości wzorców i t ekst u. Może się jednak zdarzyć,
że ilość dopasowań wzorców będzie rzędu kwadrat owego (na przykład wyszukiwanie wzorców
ze zbioru {„a”, „aa”, „aaa”, „aaaa”} w t ekście „aaaa”. A zat em złożoność algoryt mu AC t o
O(n + S
w
+ d), gdzie n jest długością t ekst u, S
w
— sumą długości wzorców a d — sumą wyst ą pień
wzorców w t ekście.
11.1
A lgor y t m B aker a
Ważnym zast osowaniem algoryt mu AC jest algoryt m Bakera, kt óry służy do wyszukiwania dwu-
wymiarowego wzorca w dwuwymiarowym t ekście.
Załóżmy, że nasz wzorzec jest macierzą o w
y
wierszach i w
x
kolumnach oraz element ach nale-
żących do alfabet u. Analogicznie t ekst jest macierzą o t
y
wierszach i t
x
kolumnach.
> Struktury danych i ich za stosowania
< 41 >
Algoryt m Bakera działa w nast ępujący sposób:
W yszukujemy kolumny wzorca w kolumnach t ekst u za pomocą algoryt mu AC. Znalezione do-
pasowania zapisujemy w dodat kowej t ablicy dwuwymiarowej hi t s[ t
x
] [ t
y
] . Kolumnom wzorca
nada jemy ident yfikat ory będące dodat nimi liczbami nat uralnymi, przy czym ist ot ne jest , aby przy-
st a jące kolumny ot rzymały t en sam ident yfikat or.
P rzykład:
wzorzec:
aba
t ekst :
abad
t ablica hi t s:
1210
bab
baba
0121
identyfikat ory kolumn:
121
cbab
0000
Liczba zna jdująca się na p ozycji hi t s[ i ] [ j ] jest ident yfikat orem kolumny wzorca, kt óra wyst ę-
puje w t ekście w kolumnie i -t ej, w wierszach od j do j + w
y
− 1. Liczba 0 oznacza brak dopasowania.
Ma jąc wyznaczoną t ablicę hi t s wyst arczy, że za p omocą algoryt mu KMP zna jdziemy wszyst -
kie wyst ą pienia słowa złożonego z kolejnych ident yfikat orów kolumn wzorca (na powyższym przy-
kładzie ”121“) w wierszach t ablicy hi t s. Wart o zauważyć, że ost at nie w
y
− 1 wierszy t ablicy hi t s
jest zawsze wypełnionych zerami i można je zignorować.
Ć w iczen ie 27. Zaimplement uj algoryt m Bakera.
J ako, że wszyst kie wzorce wyszukiwane algoryt mem AC są równej długości, złożoność algo-
ryt mu Bakera jest liniowa względem sumy wielkości t ekst u i wzorca.
12
M aski bi t owe
B inar na r epr ezent acj a zbior ów
W iemy, że dane w pamięci komput era zapisane są w p ost aci kodu binarnego. Okazuje się, że mo-
żemy t o wykorzyst ać w celu wygodnego przechowywania i przet warzania informacji o zbiorach.
Za jmiemy się 32-bit owym typami całkowit ymi dodat nimi np. unsi gned i nt . Liczba 75 w pa-
mięci ma post ać:
numer bit u
. . .
7
6
5
4
3
2
1
0
wart ość
. . .
2
7
2
6
2
5
2
4
2
3
2
2
2
1
2
0
wart ość bit u
. . .
0
1
0
0
1
0
1
1
D e fi n icja 6. M a ska b it ow a t o forma kodowania informacji o całym zbiorze w jednej
zmiennej.
Ust awienie bit u o numerze i na 1 lub 0 (mówimy czasem o „zapaleniu bit u”) informuje
o wyst ępowaniu lub braku element u i w zbiorze.
P rzykładem może być przechowywanie informacji o podzbiorach zbioru lit er alfab et u angiel-
skiego. Lit erom od a do h nada jemy numerki od 0 do 7. Zbiorowi { a, b, d, h} odpowiada zat em
maska 10001011
2
= 2
7
+ 2
3
+ 2
1
+ 2
0
= 139.
Ć w iczen ie 28. Zna jdź maskę dla zbioru { a, d, f , g} i zbiór reprezent owany przez maskę
83.
J ak w prosty sposób budować maski bit owe? Służą do t ego op erat ory bit owe, m.in:
•
a << b przesuwa bity zmiennej a o b bit ów w lewo (z prawej dop ełnia jąc zerami). Maska
reprezent ująca { a, g, h} t o zat em ( 1<<0) + ( 1<<6) + ( 1<<7) (nawiasy są ist ot ne, operacje
bit owe ma ją niski prioryt et ).
P rzykład: 10011011
2
<< 2 = 01101100
2
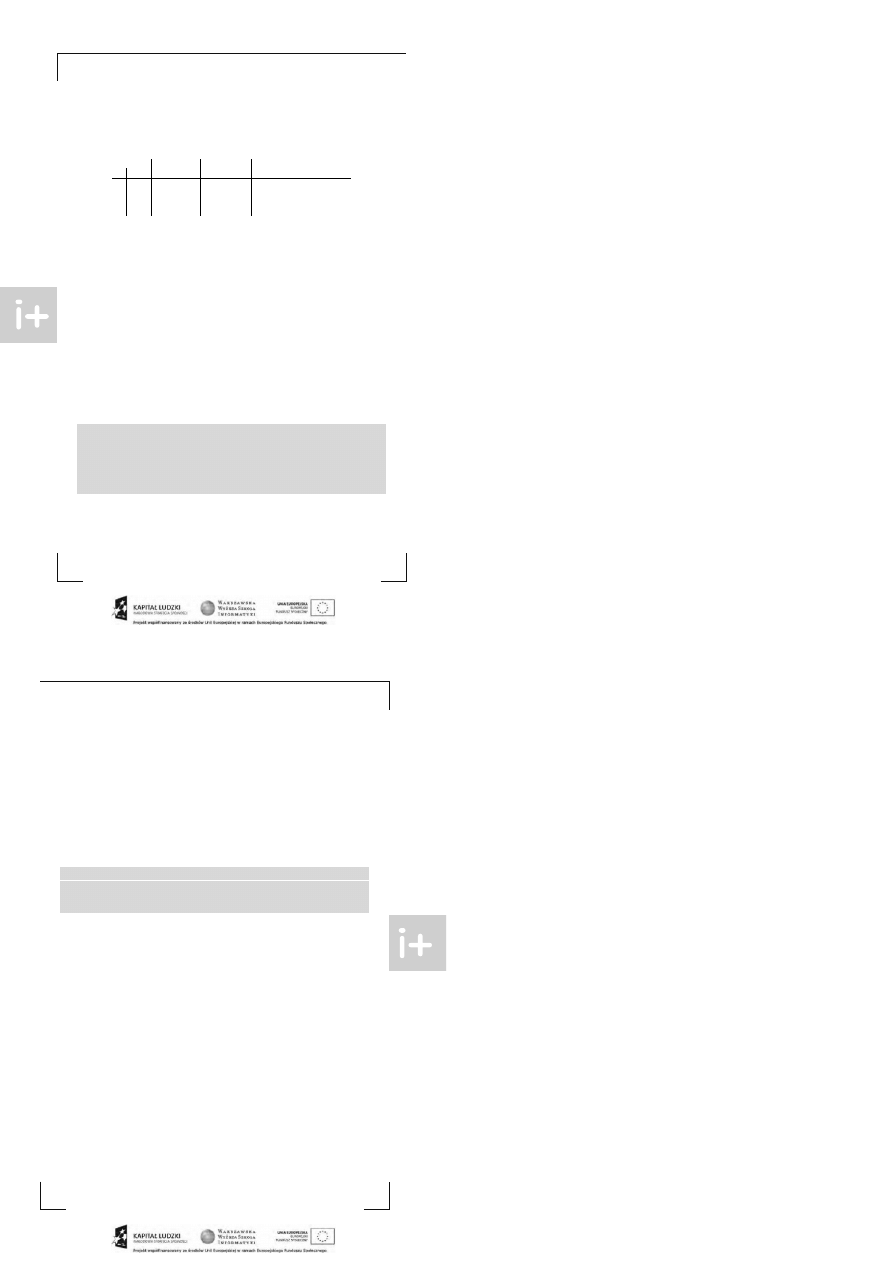
< 42 >
Informatyka +
•
a >> b przesuwa bity zmiennej a o b bit ów w prawo (z lewej dopełnia jąc zerami). Zachowuje
się t ak samo jak dzielenie (całkowit oliczbowe) przez 2
b
.
P rzykład: 10011011
2
>> 2 = 00100110
2
•
~a neguje, zamienia wszyst kich bit ów na przeciwne. Ze zbioru robi jego dopełnienie.
P rzykład: 10011011
2
= 01100100
2
Op er at or y bi t owe
Działanie operat orów bit owych na pojedynczych bit ach (i odp owiada jące im nazwy z logiki):
Zmienne
Koniunkcja
Alt ernat ywa
Alt ernat ywa wyklucza jąca
a
b
a & b
a | b
a ^ b
0
0
0
0
0
0
1
0
1
1
1
0
0
1
1
1
1
1
1
0
Wszelkie op erat ory bit owe są wykonywane niezwykle szybko, mniej więcej t ak, jak dodawanie
dwóch liczb. Ich działanie na całych zmiennych polega na wykonaniu powyższych op eracji na
każdej parze bit ów. Możemy więc szybko wykonywać operacje na zbiorach, dzięki nast ępującym
op erat orom:
•
K on iu n kcja : a & b
Przykł ad: 10011011
2
& 11001111
2
= 10001011
2
Koniunkcja jest prawdziwa t ylko jeżeli oba argumenty są prawdziwe. W związku z t ym
zast osowana do dwóch zbiorów da je ich część wspólną, bo zachowane są t e bit y, kt óre były
zapalone w obu maskach.
Tri k: ( a & ( 1<<nr ) ) ! = 0 sprawdza czy bit o numerze nr jest jedynką
•
A lt e r n a t y w a : a | b
Przykł ad: 10011011
2
| 11001111
2
= 11011111
2
Alt ernat ywa sprawdza czy choć jeden z jej argument ów jest równy 1. Zat em wynikiem al-
t ernat ywy dwóch masek jest ich suma (t eoriomnogościowa).
•
A lt e r n a t y w a w y k lu cza ją ca : a ^ b
Przykł ad: 10011011
2
^ 11001111
2
= 01010100
2
Op erację t ę częst o nazywamy zaczerpniętym z angielskiego skrót em xor . Sprawdza ona, czy
dokładnie jeden z jej argument ów jest równy 1.
Tri k: ( a ^ b) & a t o maska b ędąca różnicą zbiorów reprezent owanych przez maski a i b.
Ć w ic zen ie 29. Ma jąc dane maski reprezent ujące zbiory a, b i c zna jdź za p omocą
p owyższych operat orów:
•
część wsp ólną t ych t rzech zbiorów
•
zbiór element ów, kt óre wyst ępują w dokładnie dwóch sp ośród zbiorów a, b, c
•
różnicę zbiorów a i b, b ez użycia op erat ora ^
W szy st k i e p odzbior y
Maski bit owe bardzo zgrabnie wykorzyst ujemy w rozwiązaniach p olega jących na przejrzeniu wszyst
kich p odzbiorów. P rzykładowy problem:
Mamy dane liczby a
1
, a
2
, . . . , a
n
. Czy da się z nich wybrać podzbiór o sumie S?
> Struktury danych i ich za stosowania
< 43 >
bool odp = f al se;
/ * Maski odpowi adaj ące wszyst ki m podzbi or om zbi or u
*
* n- el ement owego t o po pr ost u l i czby od 0 do ( 1 << n) - 1
* /
i nt ogr = 1 << n;
f or ( i nt maska = 0; maska < ogr ; maska++)
{
i nt suma = 0;
/ * spr awdzamy, kt ór e el ement y są w spr awdzanym podzbi or ze * /
f or ( i nt i = 0; i < n; i ++)
i f ( ( maska & ( 1<<i ) ) ! = 0)
suma += a[ i ] ;
i f ( suma == S)
{
odp = t r ue;
br eak;
}
}
/ * Wyni k: w zmi ennej odp * /
Ć w iczen ie 30. Określ złożoność powyższego rozwiązania.
Ć w iczen ie 31. (Ambitne) Masz daną maskę bit ową reprezent ującą pewien zbiór. W jaki
prost y sposób możesz wygenerować wszyst kie podzbiory t ego zbioru?
Wskazówka: Należy je generować w odwrot nej kolejności niż w powyższym programie.
12.1
P r ogr am owanie dy nam iczne na m askach
Czasami maski bit owe st a ją się st anami w rozwiązaniach opart ych na programowaniu dynamicz-
nym. Dzieje się t ak gdy musimy zapamięt ać nie t ylko ile obiekt ów już wykorzyst aliśmy, ale t eż
dokładnie kt óre z nich. P rzyjrzyjmy się nast ępującemu problemowi:
Chcemy ułożyć w szereg n przedszkolaków. Henio i Kazio uwielbia ją st ać koło siebie, ale niest et y
Adaś i Michaś są wyraźnie wrogo do siebie nast awieni. Ogólniej, dla każdej pary przedszkolaków
wiemy, jak bardzo b ędą zadowoleni z bycia sąsiadami (dla dzieci o numerach i i j liczb ę t ę oznaczmy
przez w
i j
0). Należy wyznaczyć maksymalną sumę zadowolenia, jaka może być osią gnięt a.
Można t en problem rozwiązać sprawdza jąc wszyst kie możliwe p ermut acje przedszkolaków, w
czasie O(n ·n!). Ist nieje jednak szybszy algoryt m z wykorzyst aniem programowania dynamicznego.
P olega na rozwiązaniu wszyst kich możliwych podproblemów, t zn. znalezienia maksymalnego zado-
wolenia każdego p odzbioru dzieci, z ust alonym pewnym przedszkolakiem na końcu szeregu. W yniki
t ych p odproblemów będziemy przechowywać w t ablicy:
•
t [ mask] [ a] - maksymalne zadowolenie zbioru przedszkolaków (przechowywanego w masce
mask) w ustawieniu gdzie dziecko o numerze a jest na końcu.
Zauważmy, że jeżeli maski będziemy przeglądać po prost u w kolejności rosnącej, t o w momencie
obliczania wyniku dla p ewnego zbioru, wszyst kie jego podzbiory będą już przetworzone (będziemy
znali ich wyniki).
f or ( i nt maska = 1; maska < ( 1 << n) ; maska++)
f or ( i nt i = 0, a = 1; i < n; i ++, a <<= 1)
/ * ust al amy ost at ni e dzi ecko z danego zbi or u * /
i f ( a & maska)
{
i f ( ( a ^ maska) == 0)
{
/ * pr zypadek samot nego dzi ecka * /

< 44 >
Informatyka +
t [ maska] [ i ] = 0;
cont i nue;
}
i nt nw = 0;
f or ( i nt j = 0, b = 1; j < n; j ++, b <<= 1)
{
/ * spr awdzamy wszyst ki e możl i we pr zedost at ni e pr zedszkol aki , *
* r óżne od ost at ni ego i będące w pr zet war zanym zbi or ze
* /
i f ( j ! = i && ( b & maska) )
/ * t [ maska ^ a] [ j ] t o wyni k dl a zbi or u bez ost at ni ego dzi ecka *
* z j - t ym dzi ecki em na końcu
* /
i f ( t [ maska ^ a] [ j ] + w[ i ] [ j ] > nw)
nw = t [ maska ^ a] [ j ] + w[ i ] [ j ] ;
}
t [ maska] [ i ] = nw;
}
Ć w ic zen ie 32. J ak z wypełnionej t ablicy t uzyskać wynik dla całego zadania?
Złożoność t ego algoryt mu t o O(2
n
·n
2
). J est t o wynik ist ot nie lepszy niż O(n ·n!). P rzykładowo,
dla n = 15 nasz algoryt m p ot rzebuje około 7 milionów operacji dominujących, a rozwiązanie
„brut alne” ponad 10 bilionów!
Ć w ic zen ie 33. Rozszerz powyższy algoryt m by ot rzymać nie t ylko wart ość, ale t akże
opt ymalne rozmieszczenie dzieci.
12.2
M eet i n t he m i ddle
Meet in the middle, dosłownie „sp ot ka jmy się w połowie”, nie ma p óki co ogólnie przyjęt ej polskiej
nazwy. Zachęcam do wymyślenia czegoś!
Technika t a t o próba przyśpieszenia rozwiązań brut alnych: dzielimy wejściowy zbiór na dwa,
w każdym z nich robimy pełne przeszukiwanie, a nast ępnie st aramy się złączyć wyniki. Spróbujemy
t eraz p onownie zmierzyć się z problemem szukania podzbioru o określonej sumie.
Zast osowanie meet i n the mi ddle wygląda nast ępująco: dzielimy zbiór na dwa, w każdym z nich
generujemy wszyst kie możliwe sumy podzbiorów, sort ujemy i próbujemy dobrać pary liczb po
jednej z każdej p osort owanej list y, kt óre ma ją odpowiednią sumę.
Ć w ic zen ie 34. J ak zrealizować wyszukiwanie binarne w czasie liniowym względem dłu-
gości list ?
J ak wygląda kwest ia złożoności? Zamiast wyjściowego O(2
n
·n) ot rzymujemy O(2
n
2
·n). Zat em
asympt otycznie udało nam się zmniejszyć st ałą w wykładniku dwa razy, co jest niezłym wynikiem.
Ć w ic zen ie 35. Dokona j własnoręcznie szacowań złożoności t ego algoryt mu. Nie zapo-
mnij, że konieczne jest sort owanie!
Zadania
A. Su m a p o d zb ior u
Zaimplement uj program ilust rujący t echnikę „meet in t he middle”: masz stwierdzić czy ze
zbioru a
1
, a
2
, . . . , a
n
da się wybrać podzbiór o sumie S.
Wejście:
n S
a
1
a
2
. . . a
n
Wyj ści e:
TAK , lub NI E.
> Struktury danych i ich za stosowania
< 45 >
B. S zcze góln a w y cie czka
Mamy dany ważony, skierowany graf G o n wierzchołkach i m krawędziach. P odróżujemy w
nim między wierzchołkami o numerze 1 i n. W grafie jest t eż wyróżnione k wierzchołków
(o numerach różnych od 1 i n), przez kt óre musimy przejechać dokł adnie j eden raz. Zna jdź
minimalny czas pot rzebny na przebycie t rasy!
Wej ści e:
nm
p
1
k
1
w
1
p
2
k
2
w
2
. . .
p
n
k
n
w
n
Trójka p
i
, k
i
, w
i
oznacza, że między wierz-
chołkami p
i
oraz k
i
ist nieje krawędź o wadze
w
i
.
Wyjście:
P ojedyncza liczba - długość na jkrót szej moż-
liwej t rasy.
L i t er at ur a
1. Cormen T .H., Leiserson C.E., Rivest R.L., St ein C., Wprowadzenie do algor ytmów, W NT ,
Warszawa 2004
2. Banachowski L., Diks K., Ryt t er W ., Algorytmy i str uktury danych, W NT , Warszawa 2003
3. Diks K., Malinowski A., Ryt t er W . Waleń T ., Algor ytmy i struktury danych,
ht t p: / / wazni ak. mi muw. edu. pl / i ndex. php?t i t l e=Al gor yt my_i _st r ukt ur y_danych
4. Standard Template Li brary Programmer’ s Guide, ht t p: / / www. sgi . com/ t ech/ st l /
5. Mł odzieżowa Akademi a I nfor matyki, ht t p: / / mai n. edu. pl /
< 46 > Notatki
Informatyka +
Notatki
< 47 >

W projekcie
, poza wykładami i warsztatami,
przewidziano następujące działania:
■
24-godzinne kursy dla uczniów w ramach modułów tematycznych
■
24-godzinne kursy metodyczne dla nauczycieli, przygotowujące
do pracy z uczniem zdolnym
■
nagrania 60 wykładów informatycznych, prowadzonych
przez wybitnych specjalistów i nauczycieli akademickich
■
konkurs y dla uczniów, trzy w ciągu roku
■
udział uczniów w pracach kół naukowych
■
udział uczniów w konferencjach naukowych
■
obozy wypoczynkowo-naukowe.
Szczegółowe informacje znajdują się na stronie projektu
Wyszukiwarka
Podobne podstrony:
Łukasz Błoch Struktury danych i ich zastosowanie
Typy danych i ich klasyfikacja, INFORMATYKA, Programowanie strukturalne i obiektowe, Semestr 1
Algorytmy i struktury danych Wykład 1 Reprezentacja informacji w komputerze
Algorytmy i struktury danych Wykład 3 i 4 Tablice, rekordy i zbiory
14 Struktury i inne formy danych
Algorytmy i struktury danych, AiSD C Lista04
4 TurboPascal Struktury i typy danych
Algorytmy i struktury danych 08 Algorytmy geometryczne
Instrukcja IEF Algorytmy i struktury danych lab2
Algorytmy, struktury danych i techniki programowania wydanie 3
Algorytmy i struktury danych 1
Cw 5 Struktury Danych Materiały dodatkowe
Ściaga sortowania, algorytmy i struktury danych
ukl 74xx, Informatyka PWr, Algorytmy i Struktury Danych, Architektura Systemów Komputerowych, Archit
cw 0 1, pwr, informatyka i zarządzanie, Informatyka, algorytmy i struktury danych
AIDS w7listy, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
lab3 struktury danych
k balinska projektowanie algorytmow i struktur danych
więcej podobnych podstron