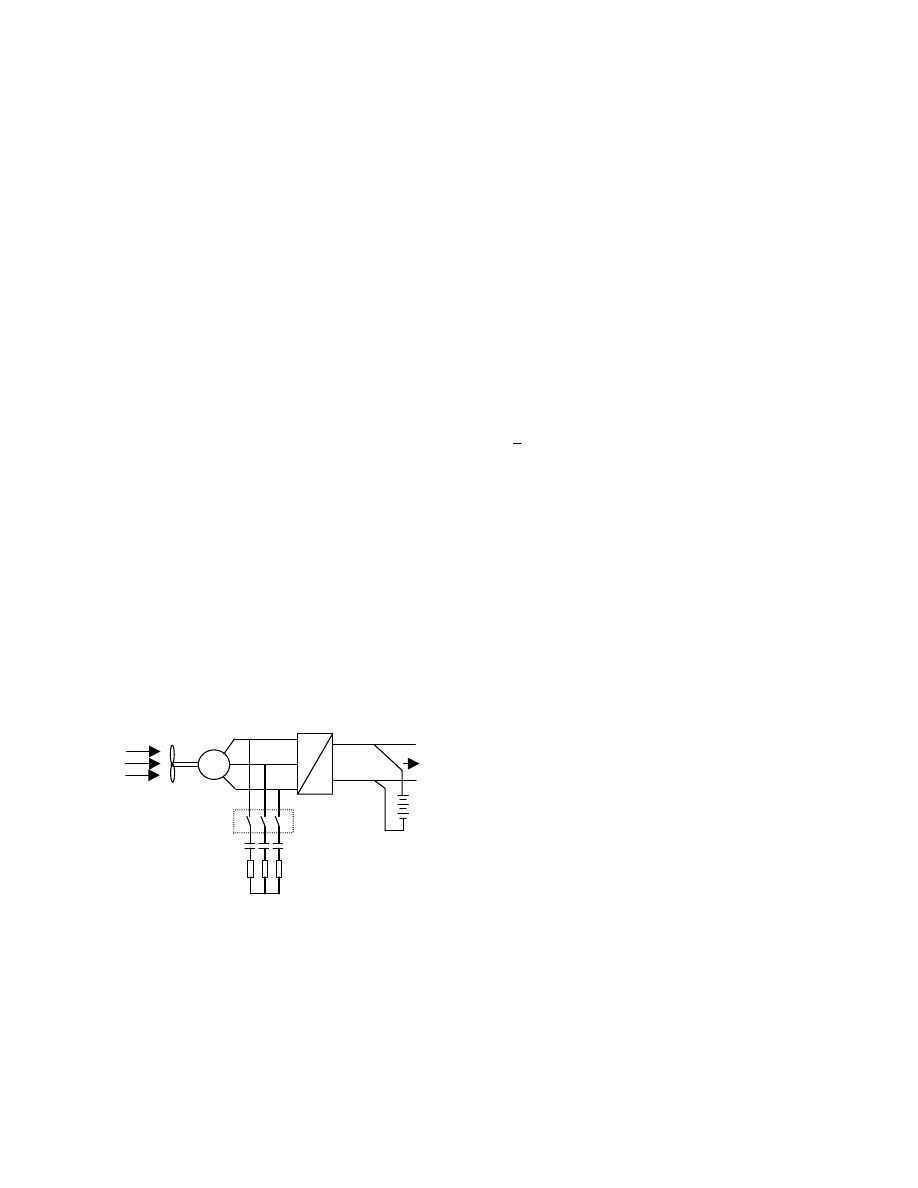
BOOST CONVERTER DESIGN FOR 20KW WIND TURBINE GENERATOR

S. Jiao, D. Patterson and S. Camilleri

NT Center for Energy Research

Northern Territory University

Darwin, NT0909

Email: [e-mail]

Tel: [phone] Fax: [phone]

Abstract

This paper presents the converter design for a 20kW wind turbine generator. The converter
consists of a phase controlled rectifier and a DC/DC boost converter. The rectifier makes the
generator AC voltage match the DC voltage while the boost converter keeps the DC voltage
constant. The generator's synchronous inductance acts as an AC inductor of boost converter so no
extra DC inductor is required. This converter is designed to be efficient and cheap. However, this
converter does result in higher power loss in the generator due to its non-sinusoidal phase current,
especially when the firing angle is not equal to 0.

1. POWER FLOW DIAGRAM

The power flow diagram for the 20kW wind generator
system is shown in Figure 1. The wind drives the wind
turbine, which is connected to the wind generator,
therefore the wind energy is converted to electrical
energy. The generator's AC voltage is converted to
DC voltage through an AC/DC converter. The DC
output voltage is fed to the load and battery bank. The
voltage should stay constant for various wind speeds.
When the wind speed is too high, i.e., the generator
produces too much power and voltage, the dump load
is connected through the switches. Also, the blade
pitch control can be employed in an emergency. When
the wind speed is low, the generator together with the
battery bank can provide sufficient energy to the load.

Figure 1. Power Flow Diagram of Wind Turbine System

In Figure 1, the battery bank is composed of 120
series connected Pd-Acid batteries, each at 2.35V and
all together at 282V. The rated speed is 10.5m/s wind
speed, 211rpm rotor speed. The wind turbine's cut-in
and cut-out wind speeds are 3m/s and 25m/s
respectively, corresponding to 60rpm and 266rpm
rotor speed. The wind energy P versus the wind
velocity v is expressed as:

3

2

1

v

AC

P

p

ρ

=

(1)

Where:

ρ

is the air density; A is the area of the air

interrupted by the wind turbine and C

p

is the

coefficient of the power of the wind turbine.

2. WIND GENERATOR

The wind generator is a three phase brushless
permanent magnet machine so the airgap flux

Φ can

be assumed to be constant. The back emf E

0

is

proportional to the rotor speed n, i.e.,

n

C

E

e

Φ

=

0

(2)

Where, C

e

is the voltage coefficient. The above

equation indicates how the wind energy is converted
to electrical energy. The generator outputs 20kW into
a resistive load at 211rpm, and up to 40kW with a
capacitive load at 266rpm for 3s or longer and
depending on its temperature rise before the overload.
The main features of the wind generator are shown in
appendix.

3. CONVERTER DESIGN

In order to make the generator's AC voltage match the
DC voltage, there are a few options. Firstly, the stator
of the generator is delta connected while the AC/DC
converter is composed of a three phase uncontrolled
rectifier and a boost converter [1]. Considering that
the synchronous inductance of the generator is large
enough to act as an AC inductor, therefore no extra
DC inductor with high frequency operation is needed
in the boost converter. The controller is cheap with
medium power loss. However, the large third
harmonics in the generator's phase voltage makes
delta connection impossible. Secondly, the stator of

G

AC

DC

Wind

BLDC

PM

Generator

Dump
Load

Switches

Load

Battery

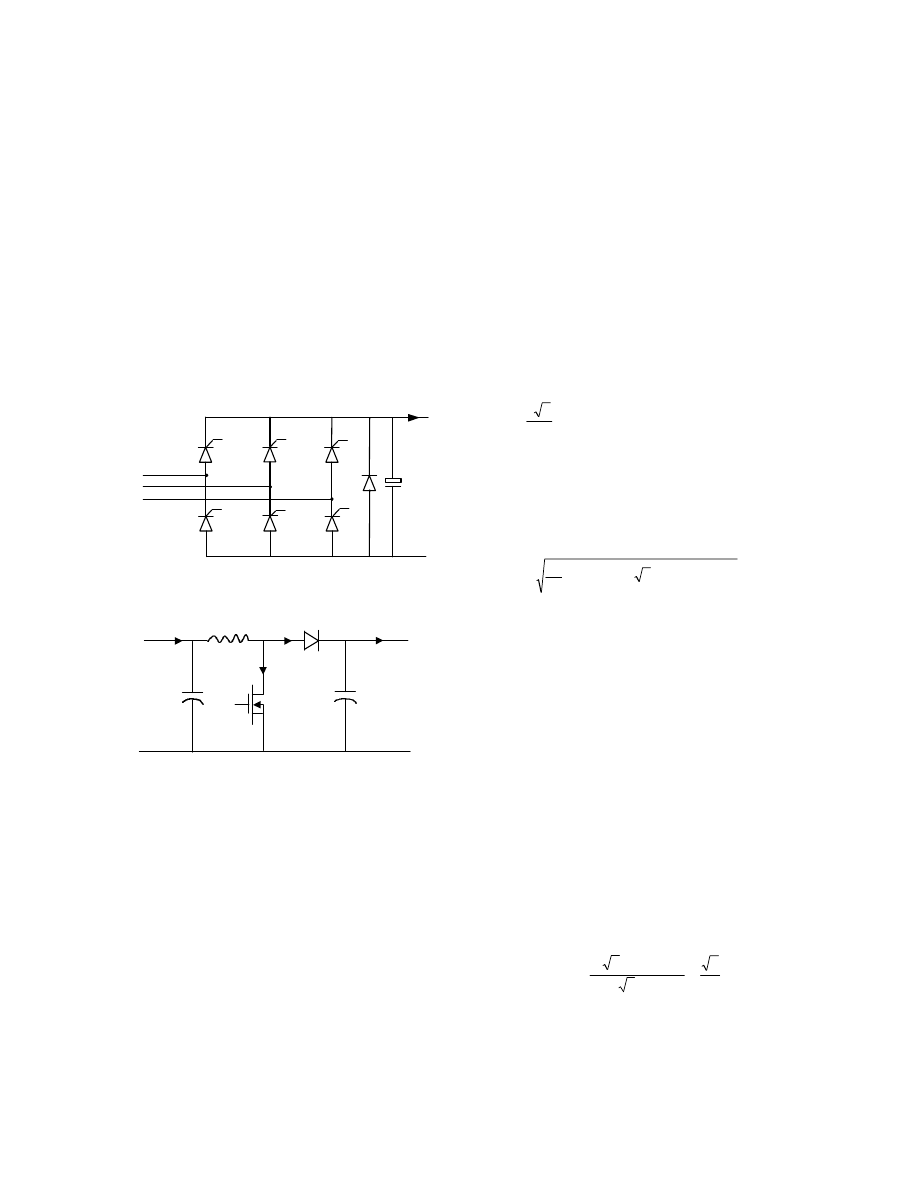
the generator is star connected while the AC/DC
converter is composed of a three phase uncontrolled
rectifier and a buck-boost converter. The buck-boost
converter can step the DC voltage up and down,
however the main difficulty is that an extra DC
inductor with high frequency operation is essential
and the power loss of buck-boost converter is high as
well. The converter is more expensive with higher and
power loss comparing to the first converter.

Another solution is that the stator of the generator
remains star connected, while the converter employs a
phase-controlled rectifier and a boost converter. The
rectifier is used to match the generator's AC voltage
and the DC voltage while the boost converter keeps
the DC voltage constant. The rectifier and the boost
converter are shown in Figure 2 and Figure 3
respectively.

Figure 2. Phase Controlled Rectifier

Figure 3. DC/DC Boost Converter

3.1 Phase-Controlled Rectifier

In Figure 2, the rectifier consists of six SCRs and a
free-wheeling diode that provides an additional path
for the load current and prevents negative values of
DC voltage from occurring. Generally, the rectifier
has three operation modes: (1) normal mode, for
example when SCR1 and SCR5 conduct. The rectifier
is likely to run at this mode considering the wind
generator's low speed operation. (2) commutation
mode, for example, when SCR1, SCR5 and SCR6
conduct. This is transition period between two
different normal modes. The commutation angle is not
negligible for this generator due to its large

synchronous reactance. (3) free-wheeling mode. This
happens when

α

>60

°

.

The advantage of a phase-controlled rectifier is that
the energy can not flow from DC side to the generator
while DC voltage is positive. However, it has some
drawbacks:

- the generator operates under unsymmetrical

load, especially at low speed.

- the phase current contains high harmonics that

increase the power loss and decrease the
efficiency.

At this stage, we neglect the commutation angle.
When the generator operates under rated speed
(n=211rpm) and rated power (P=20kW), the average
DC voltage V

avg

and its ripple are given by

U

V

V

line

avg

∆

−

α

π

=

2

cos

2

3

(3)

Here,

α

is the firing angle of SCRs. 2

∆

U is the

potential drop of the SCR and diode.

Initially, we assume

α

=0

°

, Under rated condition,

V

avg

=305.33V while 2

∆

U=3.2V.

V

d

V

V

V

avg

line

ripple

28

.

13

)

sin

2

(

2

6

3

/

2

3

/

2

=

θ

−

θ

×

π

=

∫

π

π

The average current depends on the load. Assume it is
20kW resistive load, the average and ripple current
are:

A

I

avg

50

.

65

=

,

A

I

ripple

84

.

2

=

. From the current

ripple, we can select the DC capacitor C

B

. Also, from

the maximum voltage and RMS current across the
SCR when the generator operates with 40kW
capacitive load, we can select the proper SCRs and
diode.

Assuming the load is resistive, the rectifier's DC
current and other quantities can be estimated by the
following procedures:

(1) find power P from equation (1)

(2) find fundamental frequency f from rotor speed n

(3) find back emf E

0

from equation (2)

(4) estimate the phase current from the DC current as

DC

line

DC

line

line

phase

I

V

I

V

I

I

π

=

π

=

=

6

3

)

/

2

3

(

(4)

(5) from the generator's vector diagram,

L

S

D

C

y

z

x

+

_

V

1

I

1

i

z

i

y

+

_

_

+

V

2

I

2

v

xz

C

1

SCR1

SCR4

SCR6

SCR5

SCR2

SCR3

V

a

V

b

V

c

+

_

V

I

C

B

D

]

)

2

(

[

)

6

(

3

2

)

6

3

(

]

)

2

(

[

)

6

(

]

6

3

[

]

6

[

2

)

6

3

(

)

2

(

)

(

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

0

a

DC

DC

a

DC

DC

DC

DC

a

phase

phase

phase

fL

R

I

RP

V

fL

R

I

V

R

I

V

fL

I

R

I

V

E

π

+

π

+

+

π

=

π

+

π

+

π

×

π

×

+

π

=

π

+

+

=

hence,

]}

)

2

(

[

)

6

(

3

2

{

)

6

3

(

2

2

2

2

2

0

2

2

a

DC

DC

fL

R

I

RP

E

V

π

+

π

−

−

π

=

(5)

(6) put equation (3) (neglect diode voltage drop

3.2V), (4), (5) into DC power equation i.e.,

2

2

2

DC

DC

I

V

P

=

. Solving this second order

algebraic equation, we can get the DC current,

]

)

2

(

[

216

.

1

]

)

2

(

[

4445

.

0

)

3

2

(

3

2

2

2

2

2

2

2

2

0

2

0

a

a

DC

fL

R

fL

R

P

RP

E

RP

E

I

π

+

π

+

−

−

−

−

=

(6)

For instance, when n=211rpm, E

0

=196.55V, P=20kW,

R=0.2873

Ω

, L

a

=6.514mH, f=63.3Hz, from the above

equation, I

DC

=63.26A, there is 3.3% error due to the

above assumptions such as neglecting of commutation
angle, voltage drop of diode,

α

=0

°

at this stage etc.

Here we can put a correcting factor k=1.033 in
equation (6) to reduce the error.

(7) find other quantities such as V

DC

etc. Here, V

DC

may be greater than V

2

=282V, e.g., under rated

condition. Then we need adjust the firing angle to
limit V

DC

to 282V. It follows in next step.

(8) if V

DC

≤

282V,

α

=0

°

if V

DC

>282V, find

α

from Equation (3), i.e.,

(neglecting 2

∆

U)

)

V

282

(

cos

DC

1

−

=

α

(15)

in this case, V

DC(new)

=282V.

(9) correct the I

DC

by I

DC(new)

=P/282 if V

DC

is greater

than 282V in order to output the same power.
Note that, it is assume that the fundamental
frequency of line voltage and current stay the
same as before because the power output does not
change. Therefore, we need not correct the AC
values.

For example, under the rated operating condition,
V

DC

=305.33V I

DC

=65.5A for diode rectifier, while

α=22

.54

°

, V

DC

=282V, I

DC

=70.93A for the phase-

controlled rectifier.

The switching power losses are very small for SCRs
due to low frequency operation, hence the overall
power loss of the rectifier P

B

can be taken as its

conduction loss expressed by

)

(

)

(

2

6

)

3

/

(

AV

F

TM

AV

F

TM

B

I

V

I

V

P

=

×

=

(7)

Where, V

TM

is the on-state voltage and I

F(AV)

is the

average forward current. The total loss of rectifier
under rated condition is 227W.

Figure 4 shows the rectifier's performance versus the
rotor speed with different loads, i.e., 1.0, 0.8, 0.6, 0.4,
0.2 rated load. V

1

represents the DC voltage fed to

DC/DC converter whilst V

DC

for the DC voltage in

case of diode rectifier, i.e.,

α

=0

°

. At rated load, the

rectifier takes effect for the speeds over 142rpm,
below this speed, the DC/DC boost converter is
needed to boost the DC voltage up.

3.2 DC/DC Boost Converter

The DC/DC converter is chosen to be a direct boost
converter as shown in Figure 3. Initially, it is assumed
that there is no power loss in the converter. The
voltage and current relationships between the primary
and secondary sides are shown in Equation (8) and (9)
respectively.

D

V

V

−

=

1

/

2

1

(8)

D

I

I

−

=

1

/

1

2

(9)

Here, D stands for the duty ratio, which is defined as
the ratio between the conduction time of the switch
TR and the duty period. When the generator operates
under rated condition, V

1

=V

2

=282V, I

1

=I

2

=70.92A,

hence D=0. The duty ratio versus rotor speed under
different loads is shown in Figure 5.

Figure 5. Duty Ratio versus Rotor Speed

with 1.0, 0.8, 0.6, 0.2 rated Loads

60

80

100

120

140

160

180

200

220

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

D

n(rpm)

0.2…1.0

From Figure 4 and Figure 5, it can be seen that the
converter is structured as a rectifier and a boost
converter. When the line voltage of generator is high,
the rectifier takes effect while D=0; on the other hand,
when the voltage of generator is low, the boost
converter takes effect while

α

=0

°

.

The ripple in V

2

should not be too high as the

secondary side of the boost converter is connected to
the battery bank. The primary side of the boost
converter is connected to the turbine generator via the
rectifier. The ripple in I

1,

which introduces power loss

in the generator, could be high, e.g., if the current
ripple is 10% of the DC current, the copper loss is 1%
of the main copper loss, which is only a small part of
the power loss. Note that the capacitor C

B

of the

rectifier takes the effect of C

1

. The primary voltage is

assumed to contain no harmonics after the capacitor
C

B

, therefore, the values of L and C should be

2

2

)

1

(

v

T

D

I

C

∆

−

≥

(10)

1

1

)

1

(

i

T

D

V

L

∆

−

≥

(11)

Where,

∆v

2

,

∆i

1

are voltage and current ripples

respectively. Assuming f

s

=20KHz, T=50

µ

s. Let

%

5

/

2

2

≤

∆

V

v

and

%

10

/

1

1

≤

∆

I

i

, we get C>155.4uF,

L>1.229mH.

The generator's phase inductor can be used as AC
inductor L while a DC inductor is not necessary [3-5].
There are two phases conducting at each time, so
L=2L

phase

=2

×

(2/3)

×

6.514 =8.685mH, which is larger

than required value.

In Figure 3, it is assumed that all the DC components
of current across the diode pass to the secondary side
of boost converter that forms the current I

2

while the

AC component passes to the capacitor C, the current
ripple across C in RMS value is estimated by

1

2

1

2

1

)

1

(

]

)

1

[(

)

1

(

)

(

I

D

D

D

I

D

D

DI

I

C

×

−

=

−

+

−

=

(12)

The current ripple in capacitor I

C

versus rotor speed

with full load given by Equation (1) is shown in
Figure 6. Its maximum current is I

Cmax

=5.26A which

occurs at n=118rpm with the power of 1768W. At this
stage, we can choose the proper capacitor.

The power losses of the boost converter are mainly
from the diode and switch (MOSFET). For the diode,
the conduction loss is dominant which is expressed by

2

)

(

)

(

0

RMS

F

t

AV

F

t

D

I

r

I

V

P

+

=

(12)

Figure 6. The Current Ripple in Capacitor C

Where, I

F(AV)

=(1-D)I

1

; I

F(RMS)

=(1-D)

0.5

I

1

; V

t0

is the

threshold voltage and r

T

is the slope resistance.

On the other hand, the power loss of MOSFET P

M

are

determined by its conduction loss P

M1

, off switching

loss P

M2

and on switching loss P

M3

. They are

)

(

2

1

1

on

DS

M

R

DI

P

=

(13)

f

s

M

t

f

I

V

P

1

1

2

=

(14)

r

s

M

t

f

I

V

P

1

1

3

=

(15)

Where, R

DS(on)

is the drain-source on-state resistance; t

f

and t

r

are current fall and rise time respectively.

The total losses of the boost converter are the
summation of the losses of the rectifier and the boost
converter. The total power losses and efficiencies can
be seen from Figure 7. It can be seen that The
maximum power loss is 320W when n=211rpm with
rated load. The maximum efficiency is 98.44% when
n=143rpm with 6226W output while the minimum
efficiency is 96.31% when n=60rpm with 459.87W.

4. CONCLUSION

The rectifier and the boost converter are designed for a
20kW wind generator. At various wind speeds, all the
quantities of the system including AC, DC voltages
and currents, duty ratio, power loss and efficiency can
be estimated through mathematical methods. The
generator's synchronous inductance is large enough to
act as the AC inductor of the boost converter,
therefore no extra DC inductor is required.

When the line voltage is too high, phase-controlled
rectifier is employed to limit the primary DC voltage
hence the duty ratio of boost converter is set to 0. In
this case, the power loss mainly originates from the
rectifier. On the other hand, when the line voltage is
low, set the firing angle of rectifier to 0 and the
primary voltage can be boosted to that of battery bank
through the boost converter. In this case, the power
loss of boost converter is still very low due to the low
current. Therefore, the converter is designed to be
very efficient.

60

80

100

120

140

160

180

200

220

0

1

2

3

4

5

6

IC

(A

)

n(rpm)

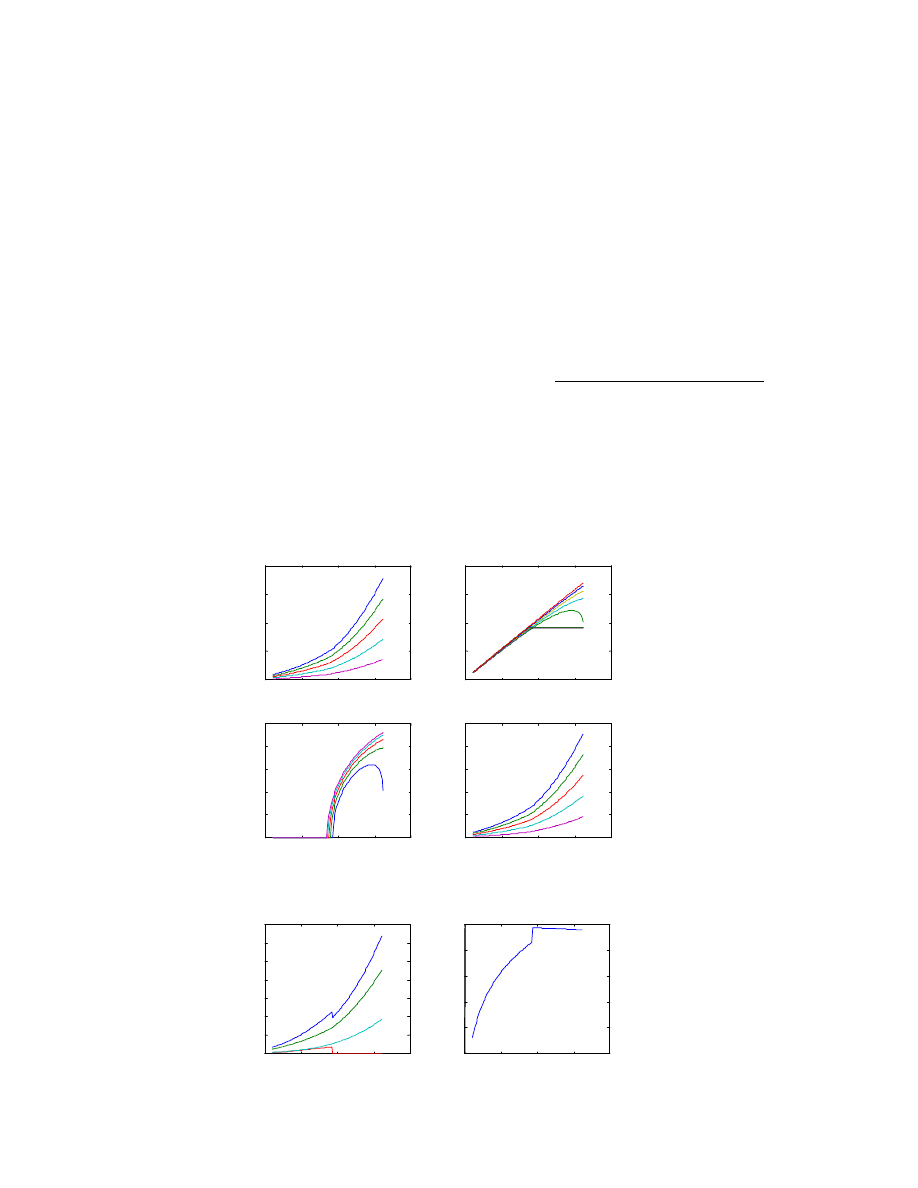
However, this converter does result in higher power
loss in the generator due to its non-sinusoidal phase
current, especially when the firing angle is not equal
to 0. A six switch voltage source converter with
closed loop current control can provide sinusoidal
current, unity power factor but it is more expensive.
The latter converter is beyond this paper and will be
introduced later.

5. ACKNOWLEGEMENT

The authors would like to thank Australian CRC for
Renewable Energy Ltd (ACRE) for the financial
support and technical support from ACRE and UTS.

6. REFERENCES

[1] Jiao, S. and Patterson, D., “Converter Design for

20kW Wind Turbine Generator with Delta
Connection”, Internal Report of ACRE, April,
1999.

[2] Jiao, S. and Patterson, D., “Buck-Boost Converter

Design for 20kW Wind Turbine Generator with
Star Connection”, Internal Report of ACRE, May,
1999.

[3] Salmon, J. C., “Reliable 3-phase PWM Boost

Rectifier Employing a Staked Dual Boost
Converter Subtopology”, IEEE Trans. on Industry
Applications, Vol. 32, No. 3, May/June 1996,
PP542-551.

[4] Salmon, J. C., “Techniques for Minimizing the

Input Current Distortion of Current-Controlled
Single Phase Boost Rectifiers”, IEEE Trans. on
Power Electronics, Vol. 8, No. 4, October 1993,
PP509-520.

[5] Salmon, J. C., “Circuit Topologies for Single-

Phase Voltage-Doubler Boost Rectifiers”, ibid,
PP542-551.

[6] Fisher, F. J., “Power Electronics”, PWS-Kent

Publishing Company, 1991.

APPENDIX: Features of 20kW Wind Generator
Rated Power Output:

20kW

Rated Speed:

211rpm

Stator Winding Connection:

star

Number of Rotor Poles:

36

Stator Phase Resistor:

0.2873

Ω

Synchronous inductance:

6.514mH

Rated Phase Current:

50.6A

Rated Phase Voltage:

131.9V

Figure 4. Performance of Phase-controlled Rectifier under 1.0, 0.8, 0.6, 0.4, 0.2 Rated Load

Figure 7. Total Power Loss and Efficiency versus Rotor Speed

50

100

150

200

250

0

20

40

60

80

ID

C

(A

)

n(rpm)

50

100

150

200

250

100

200

300

400

500

V

1

,V

D

C

(V

)

n(rpm)

50

100

150

200

250

0

10

20

30

40

50

a

(d

e

g

re

e

)

n(rpm)

50

100

150

200

250

0

50

100

150

200

250

P

B

(w

)

n(rpm)

1.0
…
0.2

0.2
…
1.0

0.2
…
1.0

1.0
…
0.2

50

100

150

200

250

0

50

100

150

200

250

300

350

,P

(t

o

ta

l)

,P

B

,P

M

,P

D

(W

)

n(rpm)

50

100

150

200

250

96

96.5

97

97.5

98

98.5

E

i(

%

)

n(rpm)

P

total

P

B

P

D

P

M