1

Syllabus

Wprowadzenie
Poprawność algorytmów (analiza algorytmów)
Sortowanie
Elementarne struktury danych
Wyszukiwanie
Zaawansowane struktury danych
Programowanie dynamiczne

2

Literatura

T. Cormen, Ch. Lieserson, R. Rivest, Wprowadzenie do Algorytmów, WNT, 1997

R. Sedgewick, Algorytmy w C++, RM, 1999

N. Wirth, Algorytmy + struktury danych = programy, WNT, 2001

3

O co w tym wszystkim chodzi?

Rozwiązywanie problemów:

– Układanie planu zajęć

– Balansowanie własnego budżet

– Symulacja lotu samolotem

– Prognoza pogody

Dla rozwiązania problemów potrzebujemy procedur, recept, przepisów –

inaczej mówiąc

algorytmów

4

Historia

Nazwa pochodzi od perskiego matematyka Muhammeda ibn Musa

Alchwarizmiego (w łacińskiej wersji Algorismus) – IX w n.e.

Pierwszy dobrze opisany algorytm – algorytm Euklidesa znajdowania

największego wspólnego podzielnika, 400-300 p.n.e.

XIX w. – Charles Babbage, Ada Lovelace.

XX w. – Alan Turing, Alonzo Church, John von Neumann

5

Struktury danych i algorytmy

Algorytm – metoda, zestaw działań (instrukcji) potrzebnych do

rozwiązania problemu

Program – implementacja algorytmu w jakimś języku programowania

Struktura danych – organizacja danych niezbędna dla rozwiązania

problemu (metody dostępu etc.)

6

Ogólne spojrzenie

Cele algorytmiczne:

- poprawność,
- efektywność,

Cele implementacji:

- zwięzłość
- możliwość powtórnego

wykorzystania

Wykorzystanie komputera:

Projektowanie programów (algorytmy, struktury danych)
Pisanie programów (kodowanie)
Weryfikacja programów (testowanie)

7

Problemy algorytmiczne

Ilość instancji danych spełniających

specyfikację wejścia może być nieskończona, np.:

posortowana niemalejąco sekwencja liczb naturalnych, o skończonej długości:

1, 20, 908, 909, 100000, 1000000000.
3, 44, 211, 222, 433.
3.
…

Specyfikacja
wejścia

?

Specyfikacja
wyjścia, jako
funkcji
wejścia

8

Rozwiązanie problemu

– Algorytm opisuje działania, które mają zostać przeprowadzone na danych

– Może istnieć wiele algorytmów rozwiązujących ten sam problem

Instancja
wejściowa (dane),
odpowiadająca
specyfikacji

algorytm

Wyniki
odpowiadające
danym
wejściowym

9

Definicja algorytmu

Algorytmem nazywamy skończoną sekwencję jednoznacznych

instrukcji pozwalających na rozwiązanie problemu, tj. na

uzyskanie pożądanego wyjścia dla każdego legalnego wejścia.

Własności algorytmów:

– określoność

– skończoność

– poprawność

– ogólność

– dokładność

10

Przykład 1: poszukiwanie

Wejście:

• uporządkowany niemalejąco ciąg n
(n >0) liczb
• liczba

a

1

, a

2

, a

3

,….,a

n

; q

j

Wyjście:

• indeks (pozycja)
odnalezionej wartości lub
NIL

2 5 4 10 11; 5

2

2 5 4 10 11; 9

NIL

11

Przykład 1: poszukiwanie liniowe

INPUT: A[1..n] – tablica liczb, q – liczba całkowita.
OUTPUT: indeks j taki, że A[j] = q. NIL, jeśli ∀

∀

∀

∀

j (1≤

≤

≤

≤

j≤

≤

≤

≤

n): A[j] ≠

≠

≠

≠

q

j←

←

←

←

1

while

j ≤

≤

≤

≤ n and A[j] ≠

≠

≠

≠

q

do

j++

if

j ≤

≤

≤

≤ n then return j

else return NIL

INPUT: A[1..n] – tablica liczb, q – liczba całkowita.
OUTPUT: indeks j taki, że A[j] = q. NIL, jeśli ∀

∀

∀

∀

j (1≤

≤

≤

≤

j≤

≤

≤

≤

n): A[j] ≠

≠

≠

≠

q

j←

←

←

←

1

while

j ≤

≤

≤

≤ n and A[j] ≠

≠

≠

≠

q

do

j++

if

j ≤

≤

≤

≤ n then return j

else return NIL

Algorytm wykorzystuje metodę siłową (

brute-force)

– przegląda kolejno

elementy tablicy.

Kod napisany jest w jednoznacznym

pseudojęzyku (pseudokodzie)

.

Wejście (INPUT) i wyjście (OUTPUT) zostały jasno określone.

12

Pseudokod

Zbliżony do Ady, C, Javy czy innego języka programowania:

– struktury sterujące (

if … then … else, pętle while i for)

– przypisanie (←)

– dostęp do elementów tablicy: A[i]

– dla typów złożonych (record lub object) dostęp do pól: A.b

– zmienna reprezentująca tablicę czy obiekt jest traktowana jak wskaźnik do

tej struktury (podobnie, jak w C).

13

Warunki początkowe i końcowe (precondition, postcondition)

Ważne jest sprecyzowanie warunków początkowego i końcowego dla

algorytmu:

– INPUT

: określenie jakie dane algorytm powinien dostać na wejściu

– OUTPUT

: określenie co algorytm powinien wyprodukować. Powinna zostać

przewidziana obsługa specjalnych przypadków danych wejściowych

14

Sort

Przykład 2: sortowanie

Wejście

ciąg n liczb

a

1

, a

2

, a

3

,….,a

n

b

1

,b

2

,b

3

,….,b

n

Wyjście

Permutacja wejściowego
ciągu

2 5 4 10 7

2 4

5 7 10

poprawność wyjścia:
Dla każdego wejścia algorytm po zakończeniu działania
powinien dać jako wynik b

1

, b

2

, …, b

n

takie, że:

• b

1

< b

2

< b

3

< …. < b

n

• b

1

, b

2

, b

3

, …., b

n

jest permutacją a

1

, a

2

, a

3

,….,a

n

poprawność wyjścia:

Dla każdego wejścia algorytm po zakończeniu działania
powinien dać jako wynik

b

1

, b

2

, …, b

n

takie, że:

•

b

1

<

b

2

<

b

3

< …. <

b

n

•

b

1

, b

2

, b

3

, …., b

n

jest permutacją

a

1

, a

2

, a

3

,….,a

n

15

Sortowanie przez wstawianie (Insertion Sort)

A

1

n

j

3

6

8

4

9

7

2

5 1

i

Strategia

• zaczynamy od “pustej ręki”

• wkładamy kartę we właściwe

miejsce kart poprzednio już

posortowane

• kontynuujemy takie postępowanie

aż wszystkie karty zostaną

wstawione

Strategia

• zaczynamy od “pustej ręki”

• wkładamy kartę we właściwe

miejsce kart poprzednio już

posortowane

• kontynuujemy takie postępowanie

aż wszystkie karty zostaną

wstawione

INPUT: A[1..n] – tablica liczb całkowitych
OUTPUT: permutacja A taka, że A[1]≤
A[2]≤ …≤A[n]

for j←2 to n

do key←A[j]

wstaw A[j] do posortowanej

sekwencji A[1..j-1]

i←j-1
while i>0 and A[i]>key

do A[i+1]←A[i]

i--

A[i+1]←key

INPUT: A[1..n] – tablica liczb całkowitych
OUTPUT: permutacja A taka, że A[1]≤
A[2]≤ …≤A[n]

for j←2 to n

do key←A[j]

wstaw A[j] do posortowanej

sekwencji A[1..j-1]

i←j-1
while i>0 and A[i]>key

do A[i+1]←A[i]

i--

A[i+1]←key

16

Analiza algorytmów

Efektywność:

– Czas działania

– Wykorzystanie pamięci

Efektywność jako funkcja rozmiaru wejścia:

– Ilość danych wejściowych (liczb, punktów, itp.)

– Ilość bitów w danych wejściowych

17

Analiza sortowania przez wstawianie

for j←2 to n

do key←A[j]

wstaw A[j] do posortowanej

sekwencji A[1..j-1]

i←j-1
while i>0 and A[i]>key

do A[i+1]←A[i]

i--

A[i+1]:=key

czas

c

1

c

2

0

c

3

c

4

c

5

c

6

c

7

ile razy
n
n-1
n-1

n-1

n-1

2

n

j

j

t

=

∑

2

(

1)

n

j

j

t

=

−

∑

2

(

1)

n

j

j

t

=

−

∑

Określany czas wykonania jako funkcję rozmiaru wejścia

18

Przypadki: najlepszy/najgorszy/średni

Najlepszy przypadek: elementy już są posortowane →

→

→

→

t

j

=1, czas wykonania

liniowy (Cn).

Najgorszy przypadek: elementy posortowane nierosnąco (odwrotnie

posortowane) →

→

→

→

t

j

=j, czas wykonania kwadratowy (Cn

2

)

Przypadek „średni” : t

j

=j/2, czas wykonania kwadratowy (Cn

2

)

19

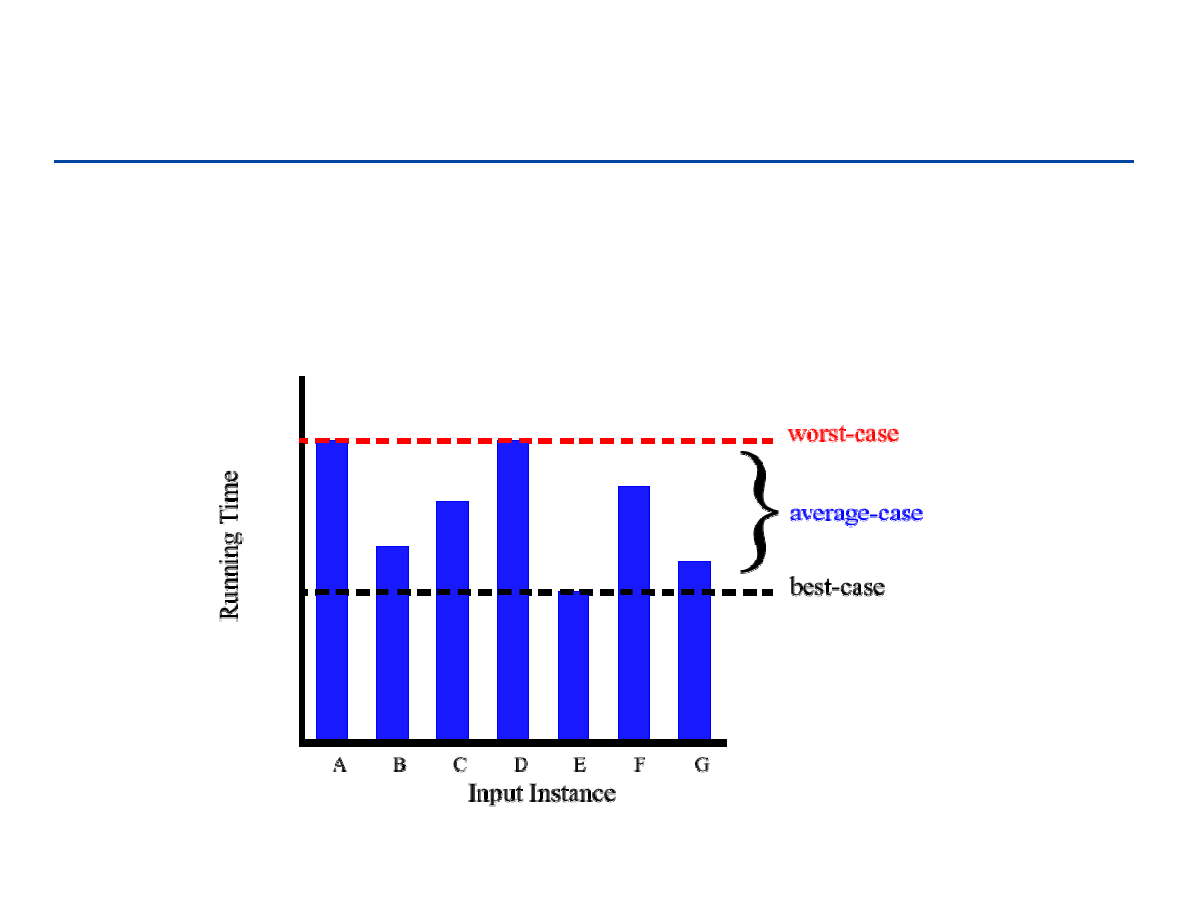
Przypadki: najlepszy/najgorszy/średni

– Dla ustalonego n czas wykonania dla poszczególnych instancji:

1n

2n

3n

4n

5n

6n

20

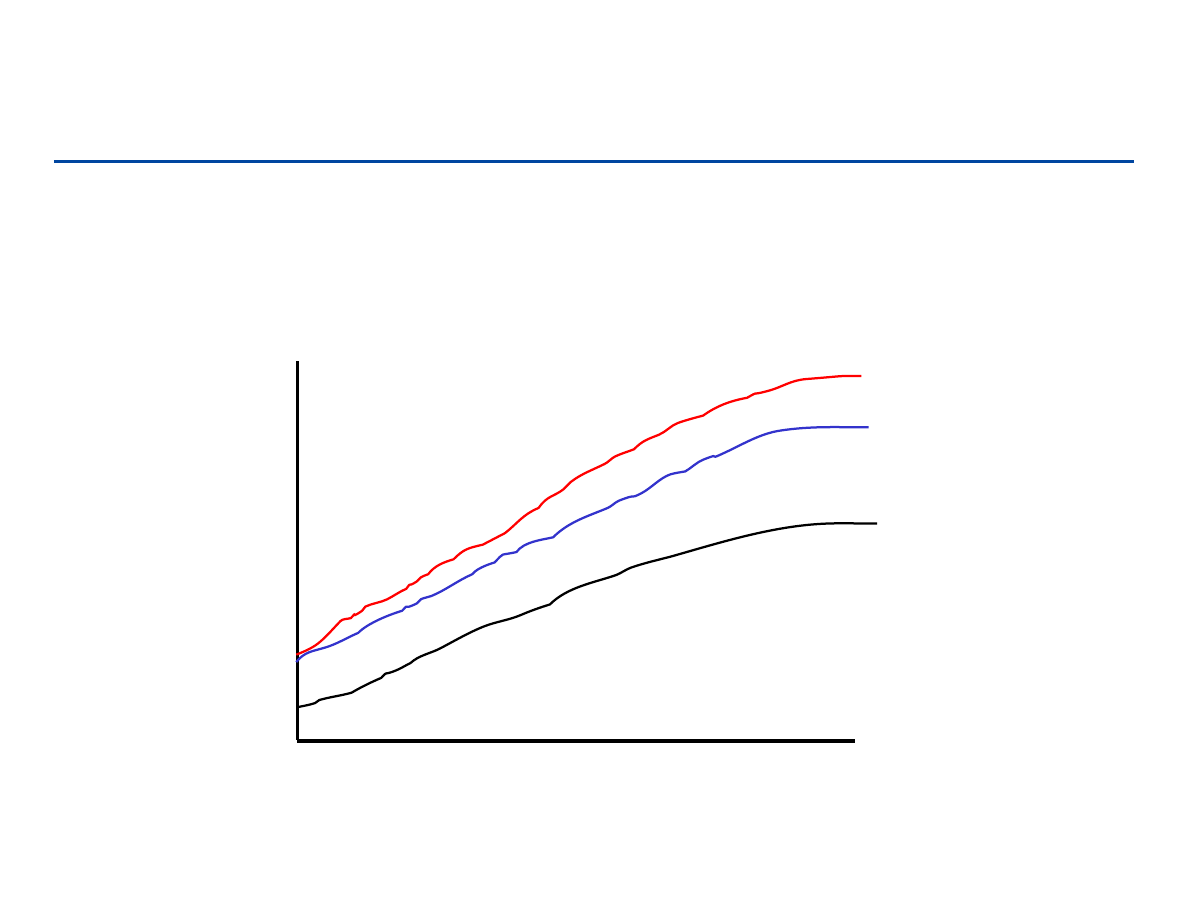
Przypadki: najlepszy/najgorszy/średni

– Dla różnych n:

1n

2n

3n

4n

5n

6n

Rozmiar wejścia

C

za

s

dz

ia

ła

ni

a

1 2 3 4 5 6 7 8 9 10 11 12 …..

najlepszy przypadek

„średni” przypadek

najgorszy przypadek

21

Przypadki: najlepszy/najgorszy/średni

Analizę najgorszego przypadku stosuje się zwykle wtedy, kiedy czas działania

jest czynnikiem krytycznym (kontrola lotów, sterowanie podawaniem leków itp.)

Dla pewnych zadań „najgorsze” przypadki mogą występować dość często.

Określenie przypadku „średniego” (analiza probabilistyczna) jest często bardzo

kłopotliwe

22

Różnice w podejściu?

Czy sortowanie przez wstawianie jest najlepszą strategią dla zadania

sortowania?

Rozważmy alternatywną strategię opartą o zasadę „dziel i zwyciężaj”:

Sortowanie przez łączenie (MergeSort):

– ciąg <4, 1, 3, 9> dzielimy na dwa podciągi

– Sortujemy te podciągi: <4, 1> i <3, 9>

– łączymy wyniki

• Czas wykonania rzędu n log n

23

Analiza wyszukiwania

INPUT: A[1..n] – tablica liczb całkowitych, q – liczba całkowita
OUTPUT: indeks j taki, że A[j] = q. NIL, jeśli ∀

∀

∀

∀

j (1≤

≤

≤

≤

j≤

≤

≤

≤

n): A[j] ≠

≠

≠

≠

q

j←

←

←

←

1

while

j ≤

≤

≤

≤ n and A[j] ≠

≠

≠

≠

q

do

j++

if

j ≤

≤

≤

≤ n then return j

else return NIL

INPUT: A[1..n] – tablica liczb całkowitych, q – liczba całkowita
OUTPUT: indeks j taki, że A[j] = q. NIL, jeśli ∀

∀

∀

∀

j (1≤

≤

≤

≤

j≤

≤

≤

≤

n): A[j] ≠

≠

≠

≠

q

j←

←

←

←

1

while

j ≤

≤

≤

≤ n and A[j] ≠

≠

≠

≠

q

do

j++

if

j ≤

≤

≤

≤ n then return j

else return NIL

Najgorszy przypadek:

C n

Średni przypadek:

C n/2

24

Poszukiwanie binarne

INPUT: A[1..n] – posortowana tablica liczb całkowitych, q – liczba całkowita.
OUTPUT: indeks j taki, że A[j] = q. NIL, jeśli ∀

∀

∀

∀

j (1≤

≤

≤

≤

j≤

≤

≤

≤

n): A[j] ≠

≠

≠

≠

q

left←

←

←

←

1

right←

←

←

←n

do

j←

←

←

←

(left+right)/2

if

A[j]=q then return j

else if

A[j]>q then right←

←

←

←

j-1

else

left=j+1

while

left<=right

return NIL

INPUT: A[1..n] – posortowana tablica liczb całkowitych, q – liczba całkowita.
OUTPUT: indeks j taki, że A[j] = q. NIL, jeśli ∀

∀

∀

∀

j (1≤

≤

≤

≤

j≤

≤

≤

≤

n): A[j] ≠

≠

≠

≠

q

left←

←

←

←

1

right←

←

←

←n

do

j←

←

←

←

(left+right)/2

if

A[j]=q then return j

else if

A[j]>q then right←

←

←

←

j-1

else

left=j+1

while

left<=right

return NIL

Pomysł: „dziel i zwyciężaj”

25

Poszukiwanie binarne - analiza

Ile razy wykonywana jest pętla:

– Po każdym przebiegu różnica między left a right zmniejsza się o

połowę

• początkowo n

• pętla kończy się kiedy różnica wynosi 1 lub 0

– Ile razy trzeba połowić n żeby dostać 1?

– lg n – lepiej niż poprzedni algorytm (n)

26

Poprawność algorytmów

27

Przegląd

Poprawność algorytmów

Podstawy matematyczne:

– Przyrost funkcji i notacje asymptotyczne

– Sumowanie szeregów

– Indukcja matematyczna

28

Poprawność algorytmów

Algorytm jest poprawny jeżeli dla każdego legalnego wejścia kończy

swoje działanie i tworzy pożądany wynik.

Automatyczne dowiedzenie poprawności nie możliwe

Istnieją jednak techniki i formalizmy pozwalające na dowodzenie

poprawności algorytmów

29

Poprawność – praktyczna i całkowita

Praktyczna

Poprawne dane

algorytm

Wynik

Jeśli

ten punkt został

osiągnięty

to

otrzymaliśmy poprawny wynik

Całkowita poprawność

Poprawne dane

algorytm

Wynik

i

otrzymamy poprawny wynik

Zawsze

ten punkt zostanie

osiągnięty

30

Dowodzenie

W celu dowiedzenia poprawności algorytmu wiążemy ze specyficznymi

miejscami algorytmu stwierdzenia (dotyczące stanu wykonania).

– np., A[1], …, A[k] są posortowane niemalejąco

Warunki początkowe (Precondition) – stwierdzenia, których prawdziwość

zakładamy przed wykonaniem algorytmu lub podprogramu (

INPUT

)

Warunki końcowe (Postcondition) – stwierdzenia, które muszą być

prawdziwe po wykonaniu algorytmu lub podprogramu (

OUTPUT

)

31

Niezmienniki pętli

Niezmienniki – stwierdzenia prawdziwe za każdym razem kiedy osiągany

jest pewien punkt algorytmu (może to zdarzać się wielokrotnie w czasie

wykonania algorytmu, np. w pętli)

Dla niezmienników pętli należy pokazać :

–

Inicjalizację – prawdziwość przed pierwszą iteracją

–

Zachowanie – jeśli stwierdzenie jest prawdziwe przed iteracją to
pozostaje prawdziwe przed następną iteracją

–

Zakończenie – kiedy pętla kończy działanie niezmiennik daje własność
przydatną do wykazania poprawności algorytmu

32

Przykład: poszukiwanie binarne (1)

inicjalizacja: left = 1, right = n niezmiennik jest prawdziwy (nie ma

elementów w [1..left-1] i [right+1..n] )

left←1
right←n
do

j←(left+right)/2
if A[j]=q then return j
else if A[j]>q then right←j-1
else left=j+1

while left<=right
return NIL

left←1
right←n
do

j←(left+right)/2
if A[j]=q then return j
else if A[j]>q then right←j-1
else left=j+1

while left<=right
return NIL

Chcemy mieć pewność, że
jeżeli zwracany jest NIL to
wartości q nie ma w tablicy A

niezmiennik: na początku
każdego wykonania pętli

while

A[i] < q dla każdego i∈[1..left-1]
oraz A[i] > q dla każdego
i∈[right+1..n]

33

Przykład: poszukiwanie binarne (2)

zachowanie: jeśli A[j]>q, to A[i] > q dla wszystkich i ∈

∈

∈

∈

[j..n], ponieważ

tablica jest posortowana. Wtedy przypisano j-1 do right. Stąd, druga

część niezmiennika również zachodzi. Analogicznie pokazuje się

pierwszą część.

left←1
right←n
do

j←(left+right)/2
if A[j]=q then return j
else if A[j]>q then right←j-1
else left=j+1

while left<=right
return NIL

left←1
right←n
do

j←(left+right)/2
if A[j]=q then return j
else if A[j]>q then right←j-1
else left=j+1

while left<=right
return NIL

niezmiennik: na początku
każdego wykonania pętli
while A[i] < q dla każdego
i∈[1..left-1] oraz A[i] > q dla
każdego i∈[right+1..n]

34

Przykład: poszukiwanie binarne (3)

Zakończenie: kiedy pętla kończy działanie, mamy left > right.

Niezmiennik oznacza, że q jest mniejsze od wszystkich elementów A na

lewo od left oraz większy od wszystkich elementów A na prawo od

right. To wyczerpuje wszystkie elementy A.

left←1
right←n
do

j←(left+right)/2
if A[j]=q then return j
else if A[j]>q then right←j-1
else left=j+1

while left<=right
return NIL

left←1
right←n
do

j←(left+right)/2
if A[j]=q then return j
else if A[j]>q then right←j-1
else left=j+1

while left<=right
return NIL

niezmiennik: na początku
każdego wykonania pętli
while A[i] < q dla każdego
i∈[1..left-1] oraz A[i] > q dla
każdego i∈[right+1..n]

35

Przykład: sortowanie przez wstawianie

niezmiennik: na początku

każdego wykonania pętli

for,

A[1…j-1] składa się z

posortowanych elementów

for j=2 to length(A)

do key

←

A[j]

i

←

j-1

while i>0 and A[i]>key

do A[i+1]

←

A[i]

i--

A[i+1]

←

key

for j=2 to length(A)

do key

←

A[j]

i

←

j-1

while i>0 and A[i]>key

do A[i+1]

←

A[i]

i--

A[i+1]

←

key

inicjalizacja:

j = 2, niezmiennik jest trywialny, A

[1] jest zawsze posortowana

zachowanie: wewnątrz pętli while przestawia się elementy A[j-1], A[j-2], …,

A[j-k] o jedną pozycję bez zmiany ich kolejności. Element

A[j]

jest wstawiany

na

k

-tą pozycję, tak że

A[k-1]≤A[k]≤A[k+1]

. Stąd

A[1..j-1]

jest

posortowane.

zakończenie: kiedy pętla się kończy (

j=n+1

) niezmiennik oznacza, że cała

tablica została posortowana.

36

Notacje asymptotyczne

Cel: uproszczenie analizy czasy wykonania, zaniedbywanie „szczegółów”,

które mogą wynikać ze specyficznej implementacji czy sprzętu

– “zaokrąglanie” dla liczb: 1,000,001 ≈ 1,000,000

– “zaokrąglanie” dla funkcji: 3n

2

≈

n

2

Główna idea: jak zwiększa się czas wykonania algorytmu wraz ze

wzrostem rozmiaru wejścia (w granicy).

– Algorytm asymptotycznie lepszy będzie bardziej efektywny dla prawie

wszystkich rozmiarów wejść (z wyjątkiem być może „małych”)

37

Notacje asymptotyczne

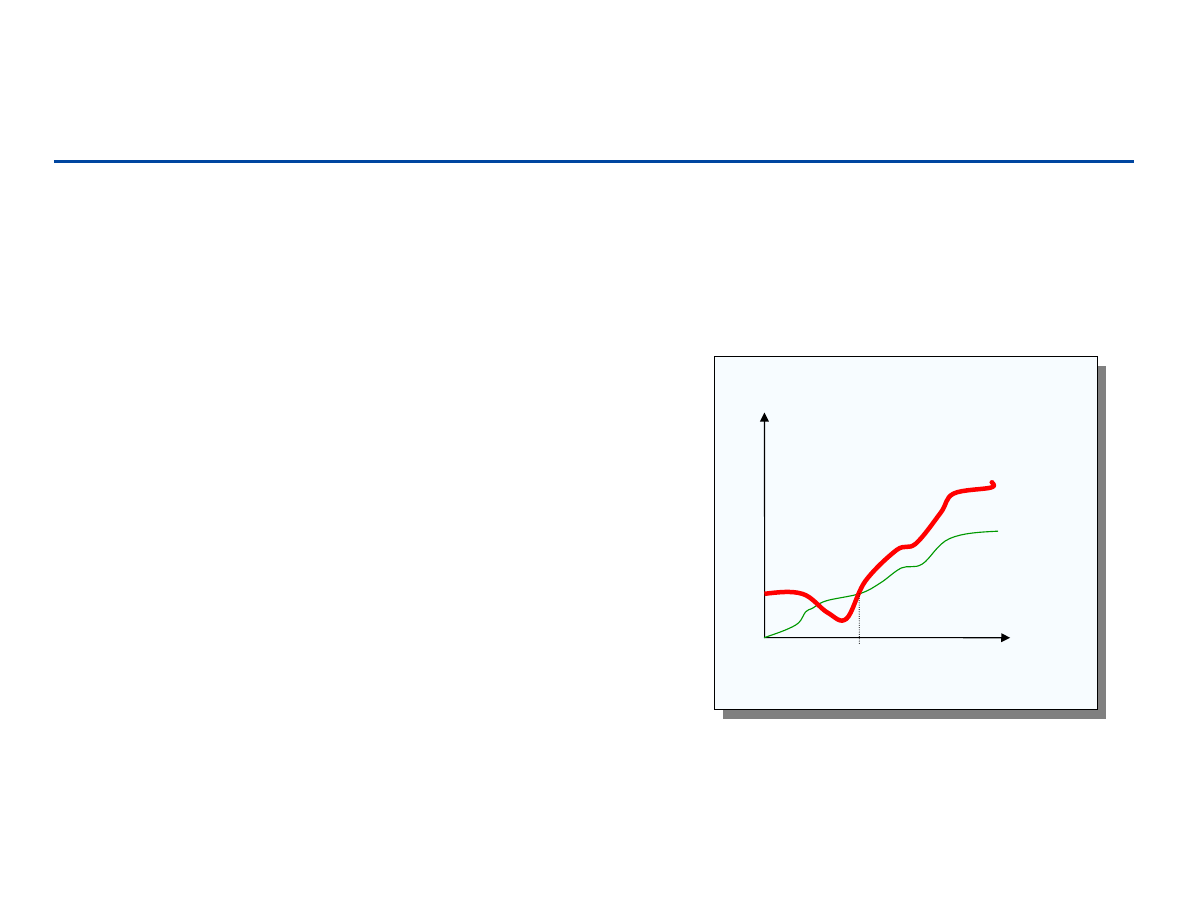
Notacja O (duże O)

– Asymptotyczne ograniczenie górne

– f(n) = O(g(n)), jeżeli istnieje stała c i n

0

,

takie, że

f(n) ≤

≤

≤

≤

c g(n) dla n ≥ n

0

– f(n) i g(n) są nieujemnymi funkcjami

całkowitymi

Korzysta się z niej przy analizie

najgorszego przypadku.

)

(

n

f

( )

c g n

⋅

0

n

Rozmiar wejścia

C

za

s

d

zi

ał

an

ia

38

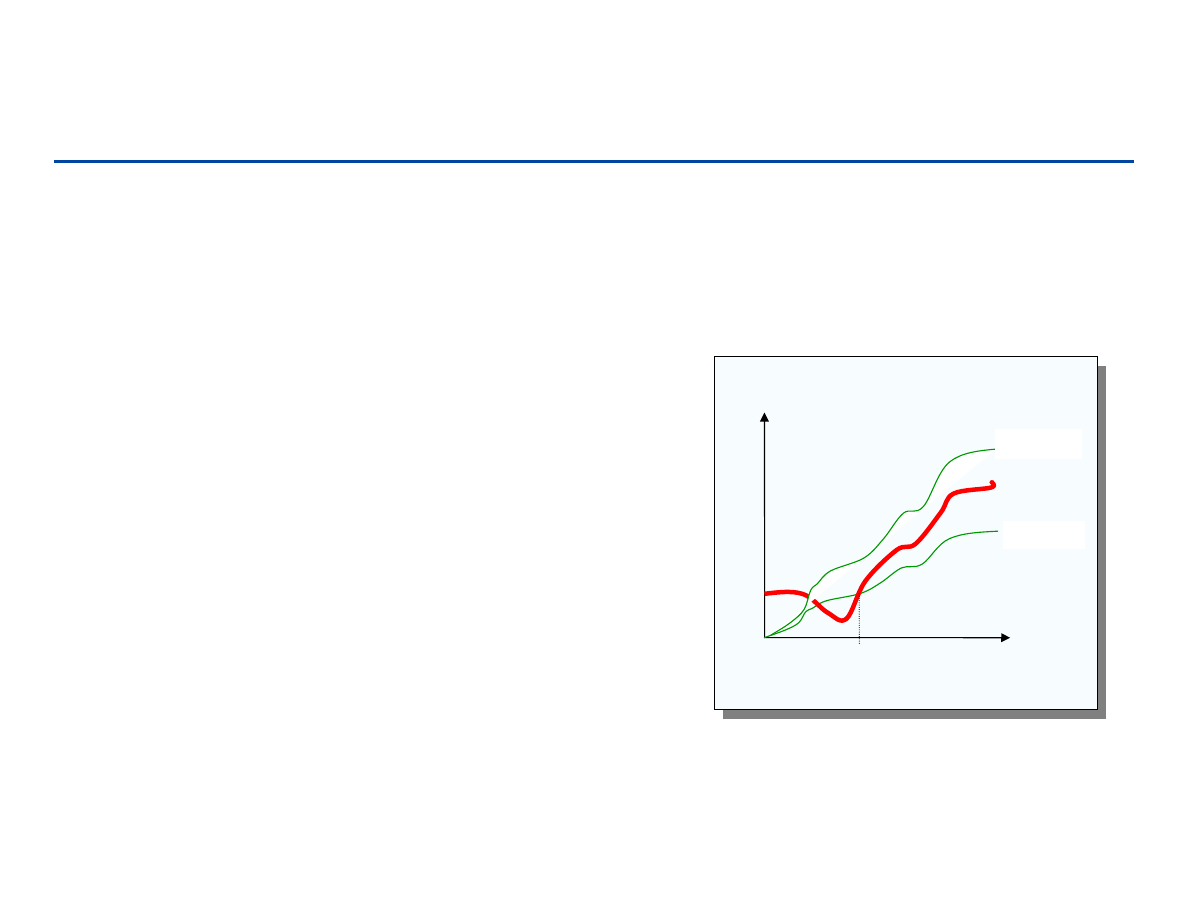
Notacja Ω

Ω

Ω

Ω

(duża Ω

Ω

Ω

Ω

)

– Asymptotyczne ograniczenie dolne

– f(n) = Ω(g(n)) jeśli istnieje stała c i n

0

,

takie, że

c g(n) ≤

≤

≤

≤

f(n) dla n ≥ n

0

Opisuje najlepsze możliwe zachowanie się

algorytmu

Rozmiar wejścia

C

za

s

d

zi

ał

an

ia

)

(

n

f

( )

c g n

⋅

0

n

Notacje asymptotyczne

39

Notacje asymptotyczne

Prosta zasada: odrzucamy mniej istotne dla czasu składniki i czynniki

stałe.

– 50 n log n jest O(n log n)

– 7n - 3 jest O(n)

– 8n

2

log n + 5n

2

+ n jest O(n

2

log n)

O jest ograniczeniem górnym więc np. (50 n log n) jest typu O(n

5

), ale

interesuje nas najlepsze możliwe oszacowanie – w tym przypadku jest to

O(n log n)

40

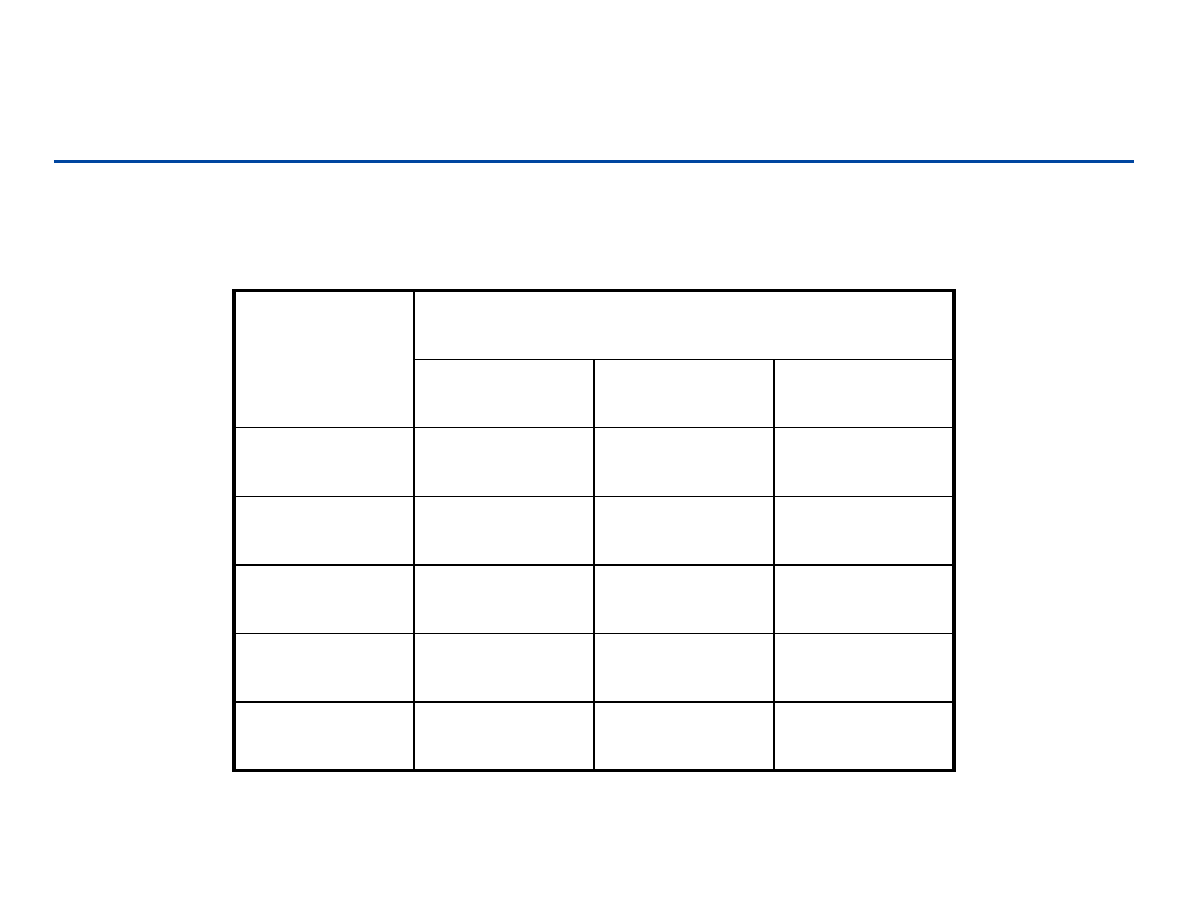
Notacja Θ

Θ

Θ

Θ ((((

duża Θ

Θ

Θ

Θ

)

– Dokładne oszacowanie asymptotyczne

– f(n) = Θ(g(n)) jeżeli istnieją stałe c

1

, c

2

, i

n

0

, takie, że

c

1

g(n) ≤

≤

≤

≤

f(n) ≤

≤

≤

≤

c

2

g(n) dla

n ≥ n

0

f(n) = Θ

Θ

Θ

Θ

(g(n)) wtedy i tylko wtedy,

gdy f(n) =

Ο

Ο

Ο

Ο

(g(n)) i f(n) = Ω

Ω

Ω

Ω

(g(n))

Rozmiar wejścia

C

za

s

d

zi

ał

an

ia

)

(

n

f

0

n

Notacje asymptotyczne

)

(

n

g

c

⋅

2

)

(

n

g

c

⋅

1

41

Notacje asymptotyczne

Istnieją dwie inne notacje asymptotyczne:

– „małe o" – f(n)=o(g(n))

mocniejsze ograniczenie analogiczne do O

• Dla każdego c, musi istnieć n

0

, takie, że

f(n) ≤

≤

≤

≤

c g(n) dla n ≥ n

0

– „mała omega" – f(n)=

ω

(g(n))

analogicznie dla

Ω

42

Notacje asymptotyczne

Analogie do zależności pomiędzy liczbami:

– f(n) = O(g(n))

≅

f ≤

≤

≤

≤

g

– f(n) = Ω(g(n))

≅

f ≥ g

– f(n) = Θ(g(n))

≅

f =

=

=

=

g

– f(n) = o(g(n))

≅

f <

<

<

<

g

– f(n) =

ω

(g(n))

≅

f >

>

>

>

g

Zwykle zapisujemy: f(n) = O(g(n)) , co formalnie powinno być rozumiane

jako f(n) ∈

∈

∈

∈

O(g(n))

43

Porównanie czasów wykonania

31

25

19

2

n

244

88

31

n

4

42426

5477

707

2n

2

7826087

166666

4096

20n log n

9000000

150000

2500

400n

1 godzina

1 minuta

1 sekunda

Maksymalny rozmiar problemu (n)

44

Szeregi

Szereg geometryczny

– Dana jest liczba całkowita n

0

i rzeczywiste 0< a

≠

1

– Szereg geometryczny reprezentuje przyrost wykładniczy

Szereg arytmetyczny

– Przyrost kwadratowy

1

2

0

1

1

...

1

n

n

i

n

i

a

a

a

a

a

a

+

=

−

= +

+

+

+

=

−

∑

0

(1

)

1 2 3 ...

2

n

i

n

n

i

n

=

+

= + + +

+

=

∑

45

Czas działania sortowania przez wstawianie jest zdeterminowany przez

zagnieżdżone pętlę

Czas wykonania pętli reprezentuje szereg

Sumowanie

2

2

(

1)

(

)

n

j

j

O n

=

−

=

∑

for j←2 to n

do key←A[j]

wstaw A[j] do posortowanej

sekwencji A[1..j-1]

i←j-1
while i>0 and A[i]>key

do A[i+1]←A[i]

i--

A[i+1]:=key

czas

c

1

c

2

0

c

3

c

4

c

5

c

6

c

7

ile razy
n
n-1
n-1

n-1

n-1

2

n

j

j

t

=

∑

2

(

1)

n

j

j

t

=

−

∑

2

(

1)

n

j

j

t

=

−

∑

46

Dowody indukcyjne

Chcemy pokazać prawdziwość własności P dla wszystkich liczb

całkowitych n ≥

≥

≥

≥

n

0

Założenie indukcyjne: dowodzimy prawdziwości P dla n

0

Krok indukcyjny: dowodzimy, że z prawdziwości P dla wszystkich k, n

0

≤

≤

≤

≤

k ≤

≤

≤

≤

n – 1 wynika prawdziwość P dla n

Przykład:

Założenie ind.

1

0

1(1 1)

(1)

2

i

S

i

=

+

=

=

∑

1

n

dla

,

2

)

1

n

(

n

i

)

n

(

S

n

0

i

≥

+

=

=

∑

=

47

Dowody indukcyjne

0

1

0

0

2

(

1)

( )

for 1 k

1

2

( )

(

1)

(

1 1)

(

2 )

(

1)

2

2

(

1)

2

k

i

n

n

i

i

k k

S k

i

n

S n

i

i

n S n

n

n

n

n

n

n

n

n n

=

−

=

=

+

=

=

≤

≤

−

=

=

+

=

−

+

=

− +

− +

=

−

+

=

=

+

=

∑

∑ ∑

Krok indukcyjny

dla

48

Metoda „dziel i zwyciężaj”

49

Wprowadzenie

Technika konstrukcji algorytmów

dziel i zwyciężaj.

przykładowe problemy:

– Wypełnianie planszy

– Poszukiwanie (binarne)

– Sortowanie (sortowanie przez łączenie - merge sort).

50

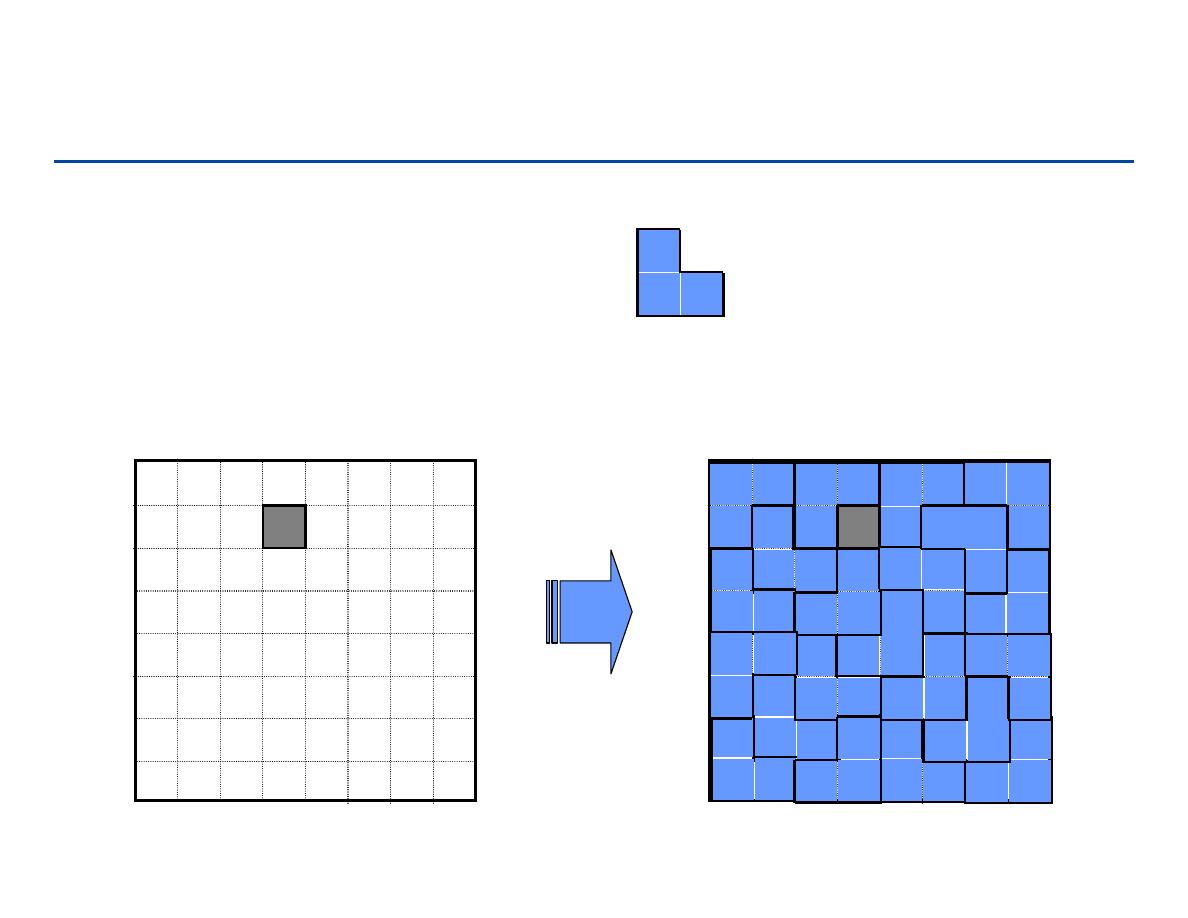
Wypełnianie planszy

Zadanie: dysponując klockami

oraz planszą 2

n

x2

n

z

brakującym polem:

Wypełnić plansze w
całości:

51

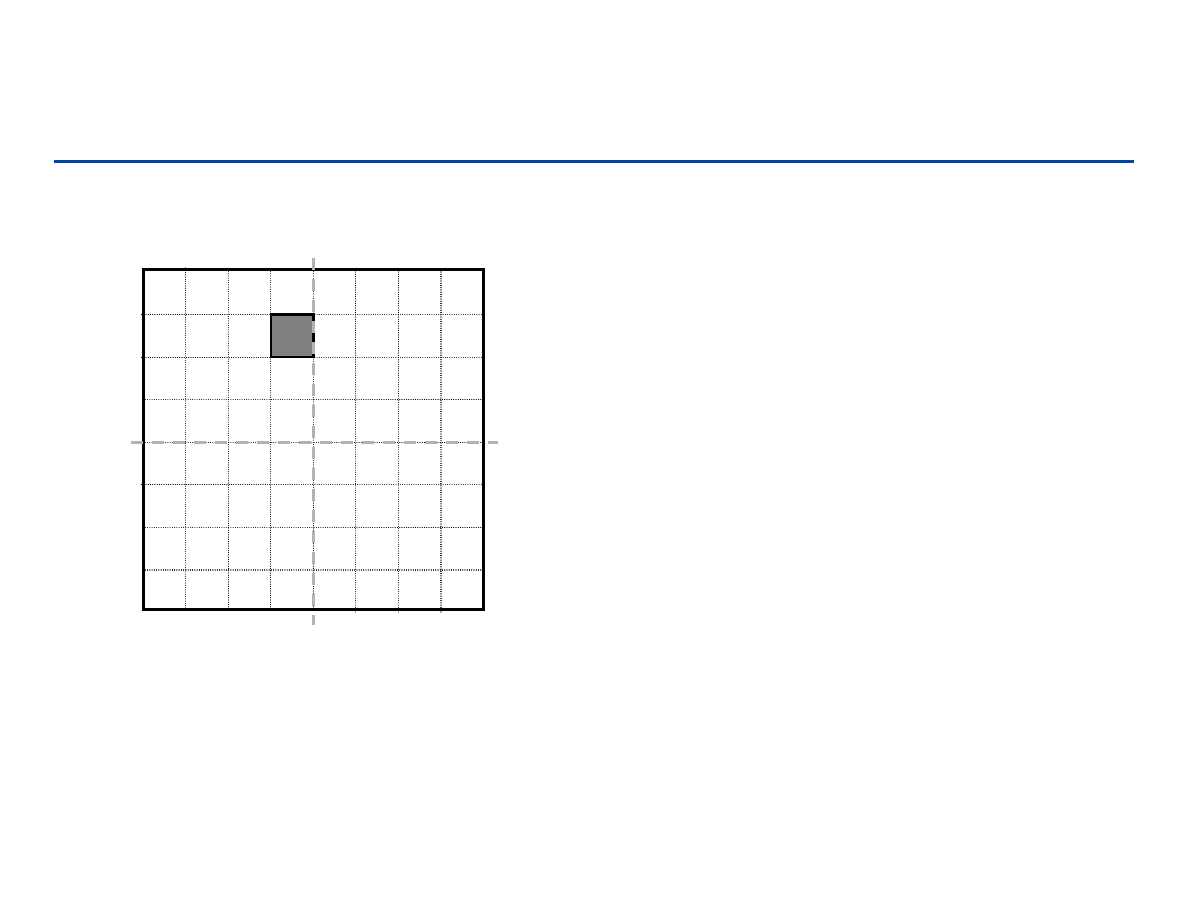
Wypełnianie planszy: przypadki trywialne (n = 1)

Przypadek trywialny (n = 1): wypełniamy plansze jednym klockiem:

Idea dla rozwiązania problemu – doprowadzić
rozmiar zadania do przypadku trywialnego, który
umiemy rozwiązać

52

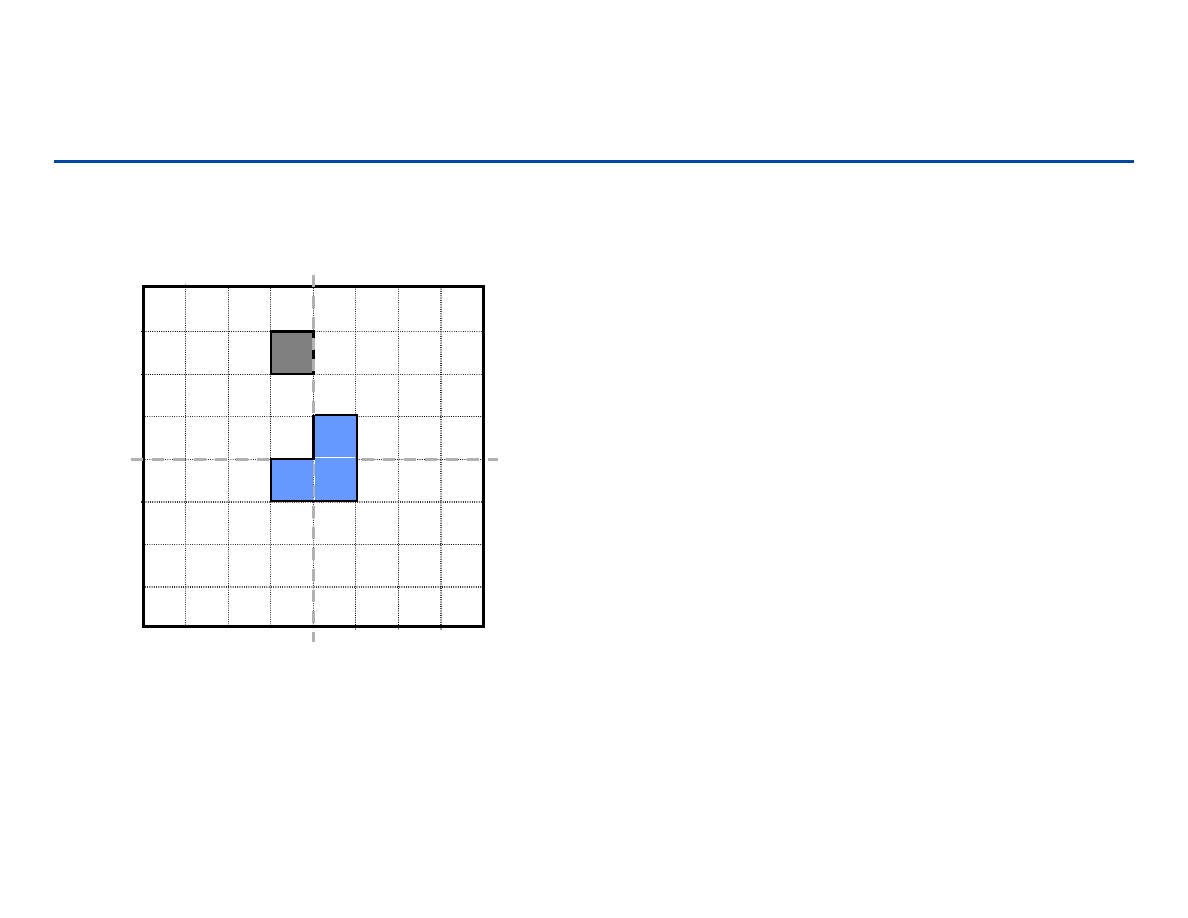
Wypełnianie planszy : podział zadania

Oryginalną planszę dzielimy na 4 części

Dostajemy problemy o rozmiarze 2

n-1

x2

n-1

Ale: trzy z nich nie są podobne do
oryginalnego (plansze nie mają brakującego
pola)!

53

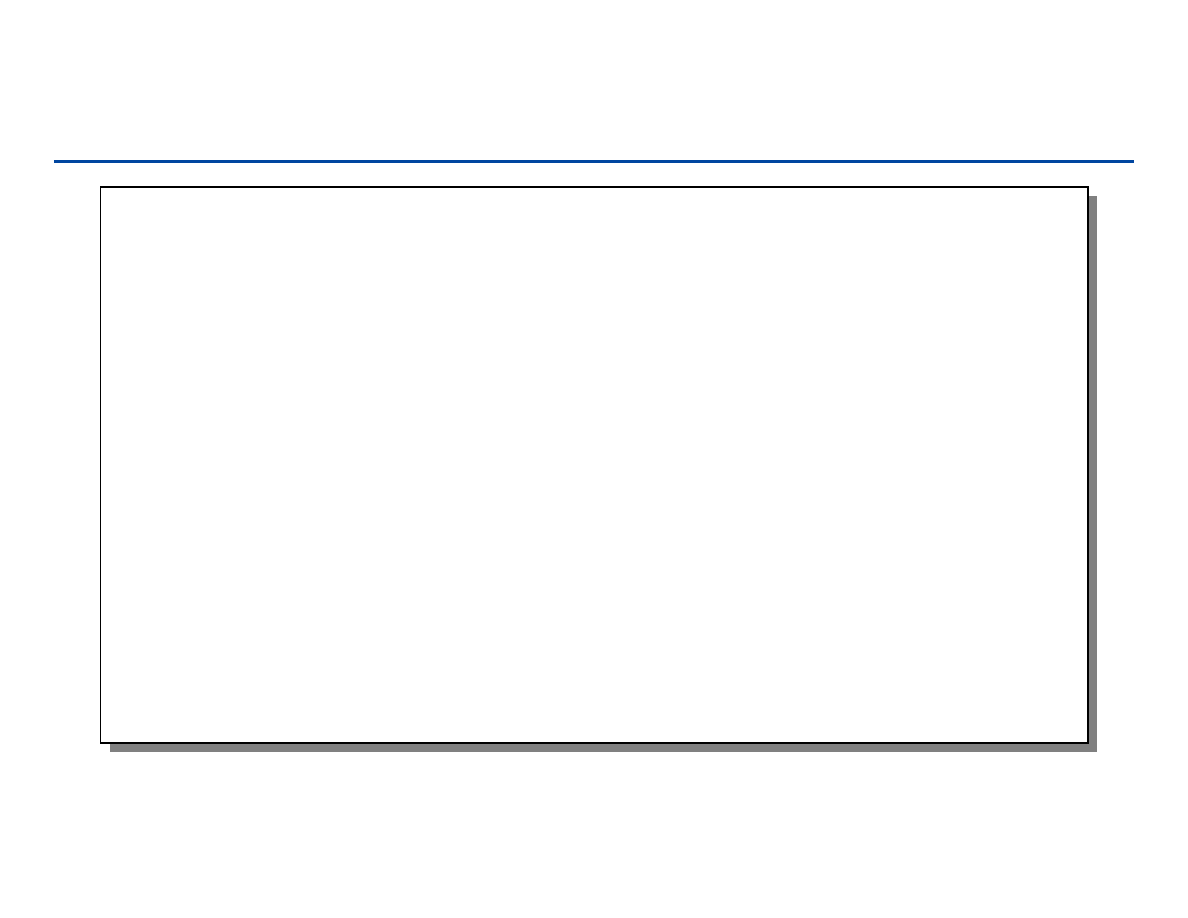
Wypełnianie planszy : podział zadania

pomysł: umieszczamy jeden klocek w środku planszy i dokonujemy

podziału na 4 części

Teraz otrzymujemy 4 plansze o rozmiarach 2

n-1

x2

n-1

.

Każda z planszy ma brakujące pole

54

Wypełnianie planszy : algorytm

INPUT: n – plansza 2

n

x2

n

, L – pozycja brakującego pola.

OUTPUT: wypełniona plansza

Tile

(n, L)

if

n = 1 then
przypadek trywialny
wypełnij jednym klockiem
return

umieść jeden klocek w środku planszy
podziel planszę na 4 równe części
Niech L1, L2, L3, L4 oznaczają pozycje 4 brakujących pól

Tile

(n-1, L1)

Tile

(n-1, L2)

Tile

(n-1, L3)

Tile

(n-1, L4)

INPUT: n – plansza 2

n

x2

n

, L – pozycja brakującego pola.

OUTPUT: wypełniona plansza

Tile

(n, L)

if

n = 1 then

przypadek trywialny

wypełnij jednym klockiem
return

umieść jeden klocek w środku planszy
podziel planszę na 4 równe części
Niech L1, L2, L3, L4 oznaczają pozycje 4 brakujących pól

Tile

(n-1, L1)

Tile

(n-1, L2)

Tile

(n-1, L3)

Tile

(n-1, L4)

55

Dziel i zwyciężaj

Metoda konstrukcji algorytmów „Dziel i zwyciężaj” :

– Jeśli problem jest na tyle mały, że umiesz go rozwiązać - zrób to. Jeśli nie

to:

•

Podział: Podziel problem na dwa lub więcej rozdzielnych

podproblemów

•

Rozwiązanie: Wykorzystaj metodę rekurencyjnie dla rozwiązania tych

podproblemów

•

Łączenie: połącz rozwiązania podproblemów tak, aby rozwiązać

oryginalny problem

56

Wypełnianie planszy : Dziel i zwyciężaj

Wypełnianie jest przykładem algorytmu „dziel i zwyciężaj” :

– w wypadku trywialnym (2x2) – po prostu wypełniamy planszę, lub:

–

Dzielimy planszę na 4 mniejsze części (wprowadzając wypełnione miejsce

w rogu, przez umieszczenie centralnie jednego klocka)

–

Rozwiązujemy problem rekursywnie stosując tą samą metodę

–

Łączymy części umieszczając klocek w środku planszy

57

Odnaleźć

liczbę w posortowanej tablicy:

– Przypadek trywialny – tablica jest jednoelementowa

– Albo

dzielimy tablice na dwie równe części i rozwiązujemy zadanie

osobno dla każdej z

nich

Poszukiwanie binarne

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.
OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli ∀j (1≤j≤n): A[j] ≠ s
Binary-search(A, p, r, s):

if p = r then

if A[p] = s then return p

else return NIL

q←(p+r)/2

ret ←

Binary-search(A, p, q, s)

if ret = NIL then

return Binary-search(A, q+1, r, s)

else return ret

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.
OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli ∀j (1≤j≤n): A[j] ≠ s
Binary-search(A, p, r, s):

if p = r then

if A[p] = s then return p

else return NIL

q←(p+r)/2

ret ←

Binary-search(A, p, q, s)

if ret = NIL then

return Binary-search(A, q+1, r, s)

else return ret

58

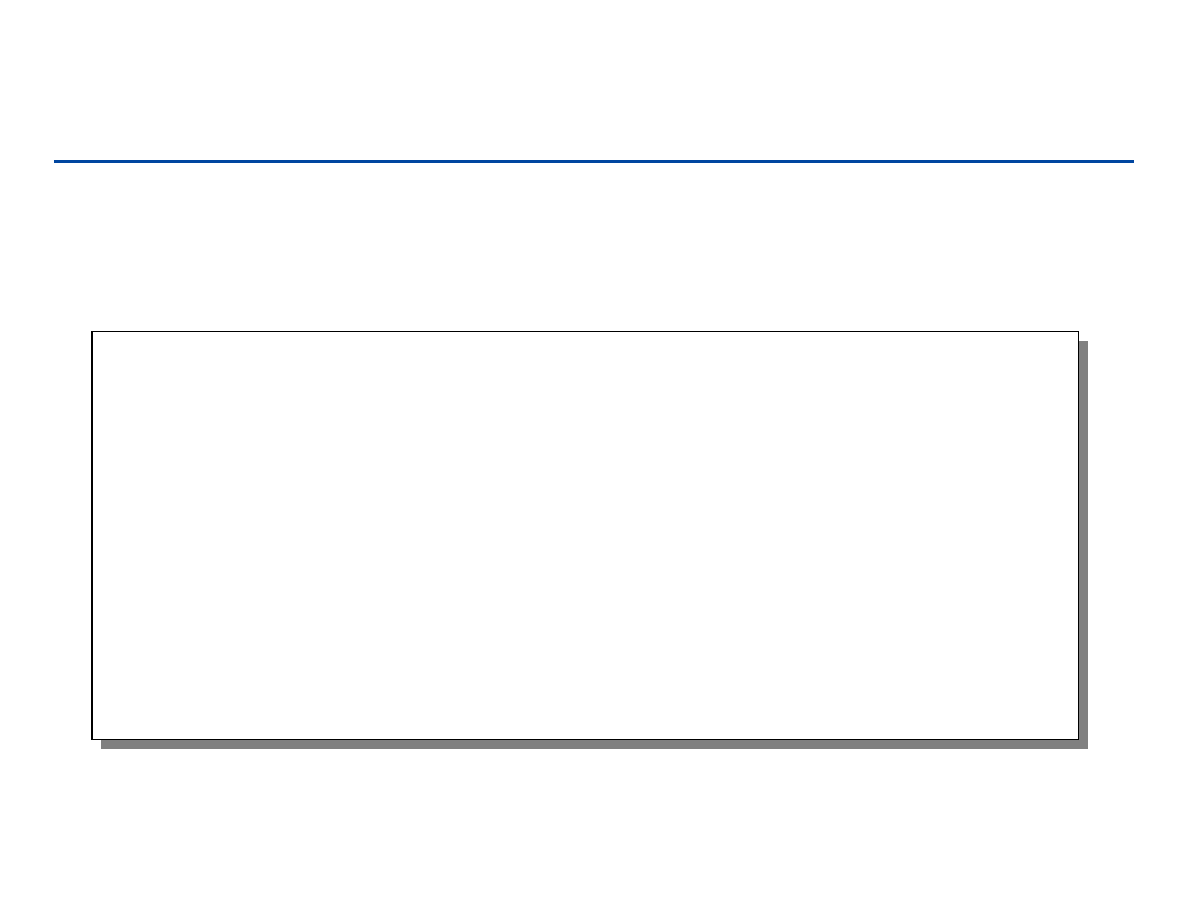
Rekurencja

Czas działania algorytmu z odwołaniami rekursywnymi można opisać poprzez

rekurencję

Równanie/nierówność opisująca funkcję poprzez jej wartości dla mniejszego

argumentu

Przykład: poszukiwanie binarne

Po rozwiązaniu daje to złożoność O(n)! – taką samą jak dla metody naiwnej

(1)

if

1

( )

2 ( / 2)

(1) if

1

n

T n

T n

n

Θ

=



=



+ Θ

>



59

Poszukiwanie binarne (poprawione)

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.

OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli ∀j (1≤j≤n): A[j] ≠s

Binary-search

(A, p, r, s):

if

p = r then

if

A[p] = s then return p

else return

NIL

q←

←

←

←

(p+r)/2

if

A[q] ≤

≤

≤

≤

s then return Binary-search(A, p, q, s)

else return Binary-search

(A, q+1, r, s)

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.

OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli ∀j (1≤j≤n): A[j] ≠s

Binary-search

(A, p, r, s):

if

p = r then

if

A[p] = s then return p

else return

NIL

q←

←

←

←

(p+r)/2

if

A[q] ≤

≤

≤

≤

s then return Binary-search(A, p, q, s)

else return Binary-search

(A, q+1, r, s)

T(n) = Θ(n) – nie lepiej niż dla metody siłowej!

Poprawa: rozwiązywać zadanie tylko dla jednej połowy tablicy

60

Czas działania metody

T(n) = Θ

Θ

Θ

Θ

(lg n) !

(1)

if

1

( )

( / 2)

(1) if

1

n

T n

T n

n

Θ

=



=



+ Θ

>



61

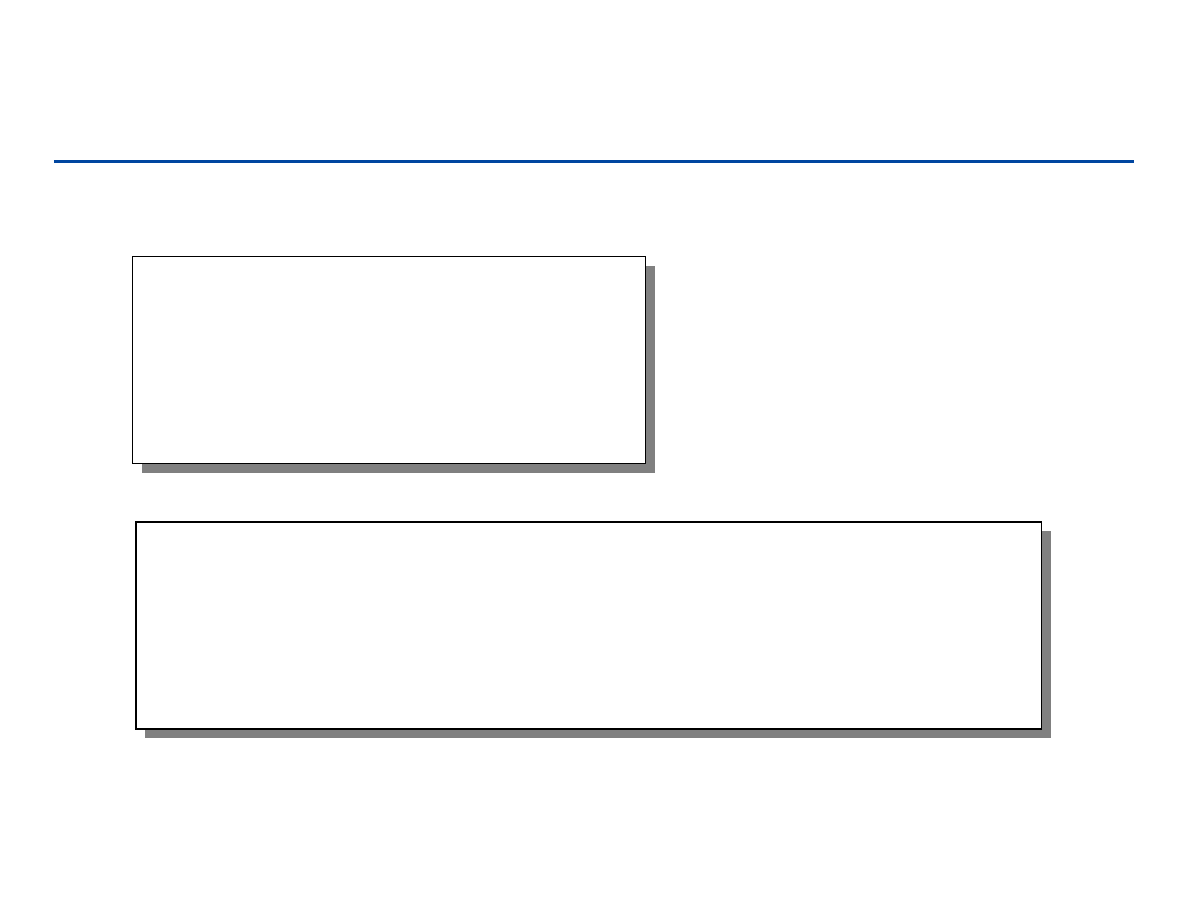
Sortowanie przez łączenie (merge sort)

Podziel: Jeśli S posiada przynajmniej dwa elementy (1 lub 0 elementów –

przypadek trywialny), podziel S na dwie równe (z dokładnością do 1

elementu) części S

1

i S

2

. (tj. S

1

zawiera pierwsze n/2 elementów, a S

2

kolejne n/2).

Zwyciężaj: posortuj sekwencje S

1

i S

2

stosując Merge Sort.

Połącz: Połącz elementy z dwóch posortowanych sekwencji S

1

i S

2

w

sekwencję S zachowaniem porządku

62

Algorytm – Merge Sort

Merge-Sort(A, p, r)

if p < r then

q← (p+r)/2
Merge-Sort(A, p, q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)

Merge-Sort(A, p, r)

if p < r then

q← (p+r)/2
Merge-Sort(A, p, q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)

Merge(A, p, q, r)

wybieramy mniejszy z dwóch elementów na początku

sekwencji A[p..q] oraz A[q+1..r] i wkładamy go do
sekwencji wynikowej, przestawiamy odpowiedni znacznik.
Powtarzamy to aż do wyczerpania się elementów.
Rezultat kopiujemy do A[p..r].

Merge(A, p, q, r)

wybieramy mniejszy z dwóch elementów na początku

sekwencji A[p..q] oraz A[q+1..r] i wkładamy go do
sekwencji wynikowej, przestawiamy odpowiedni znacznik.
Powtarzamy to aż do wyczerpania się elementów.
Rezultat kopiujemy do A[p..r].

63

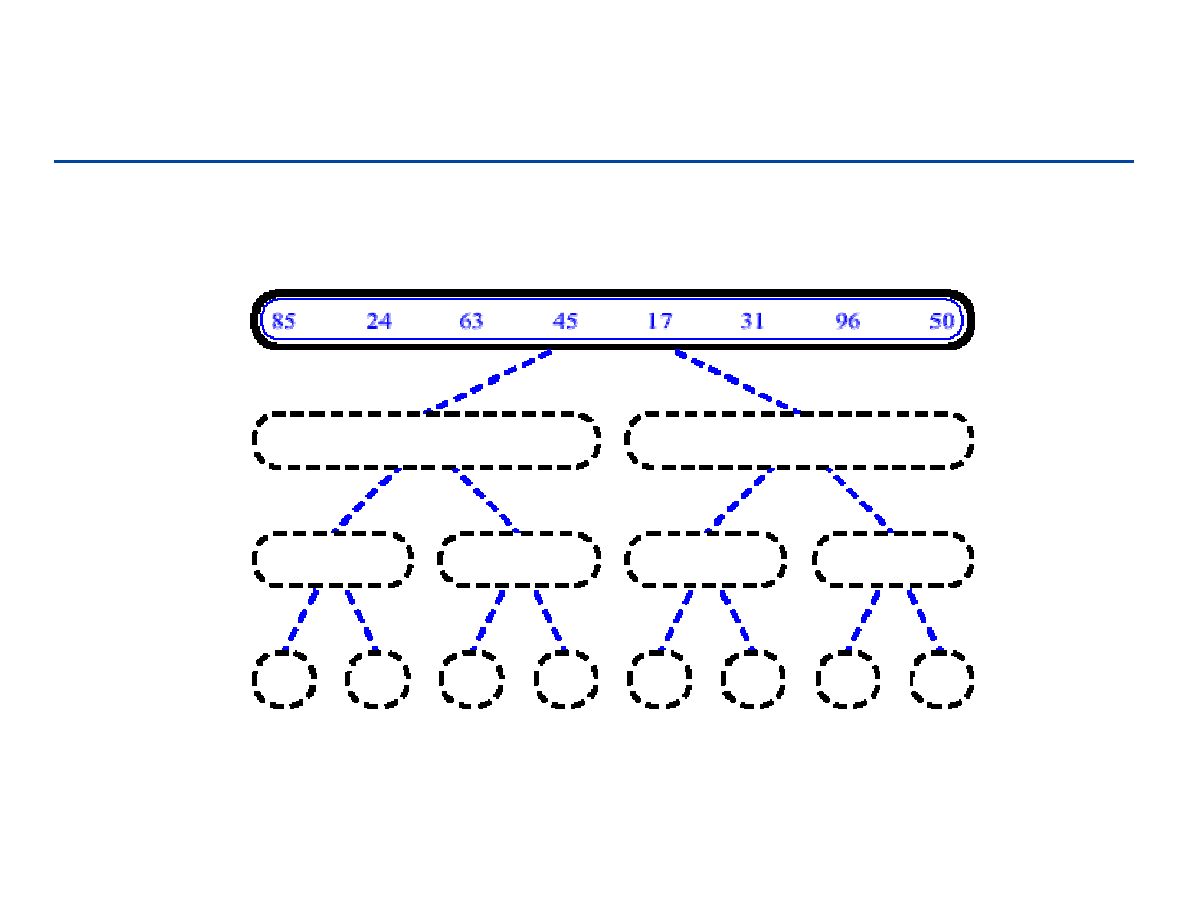
Sortowanie przez łączenie - 1

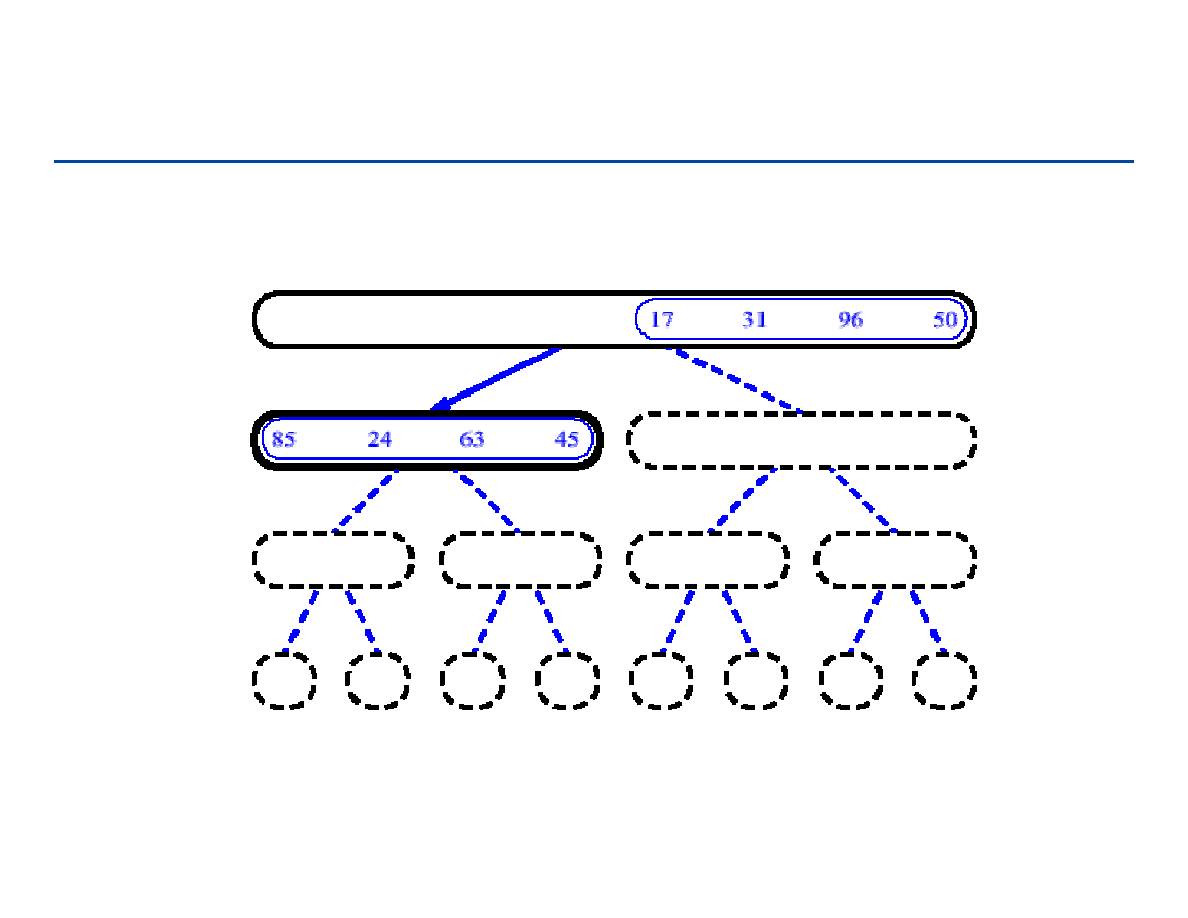
64

Sortowanie przez łączenie - 2

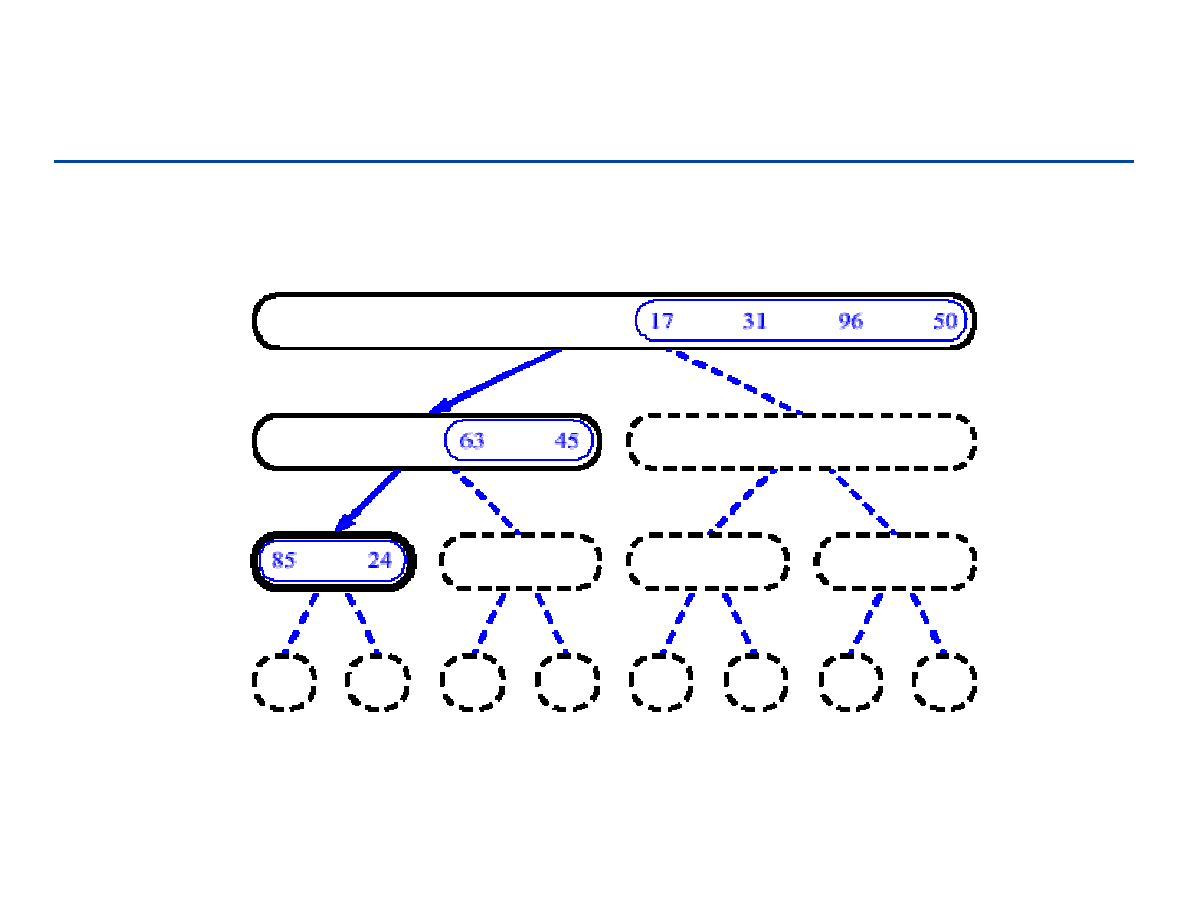
65

Sortowanie przez łączenie - 3

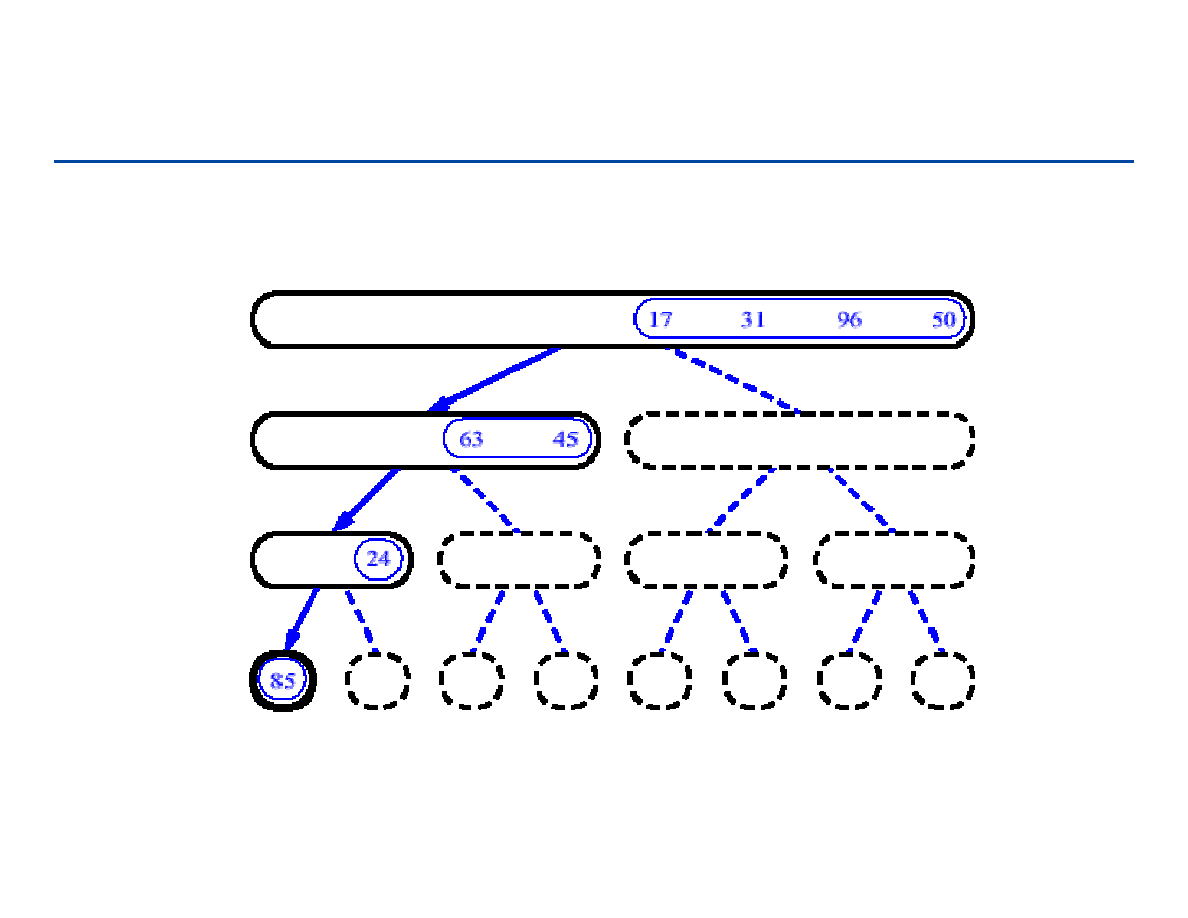
66

Sortowanie przez łączenie - 4

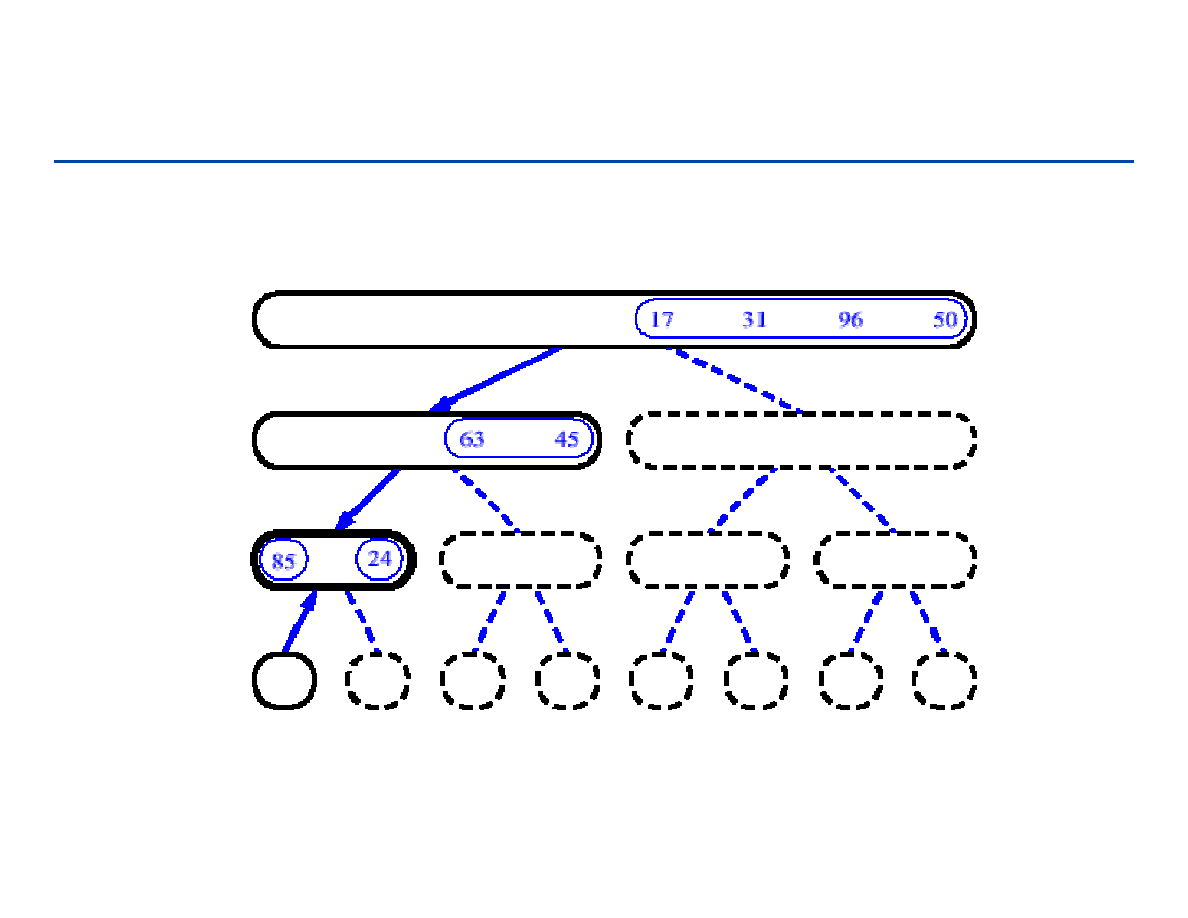
67

Sortowanie przez łączenie - 5

68

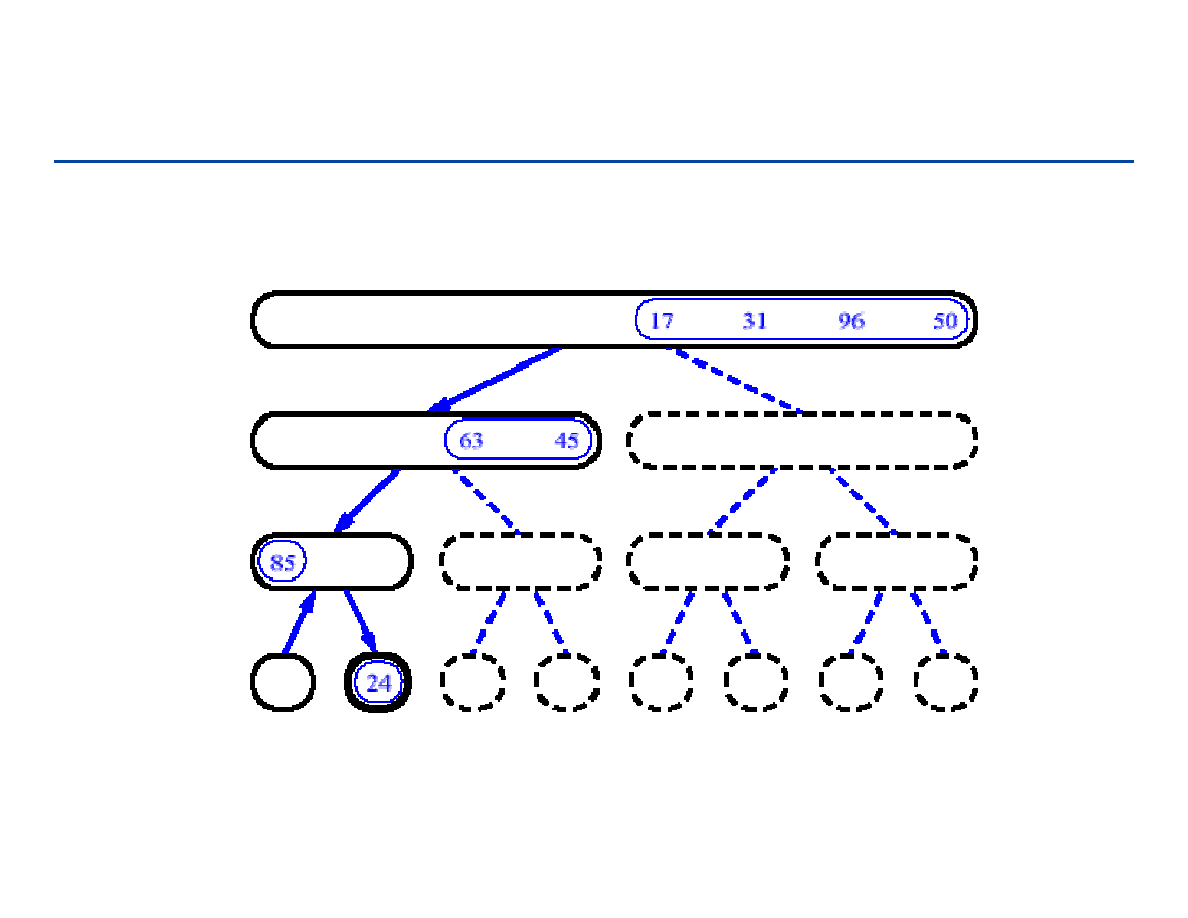
Sortowanie przez łączenie - 6

69

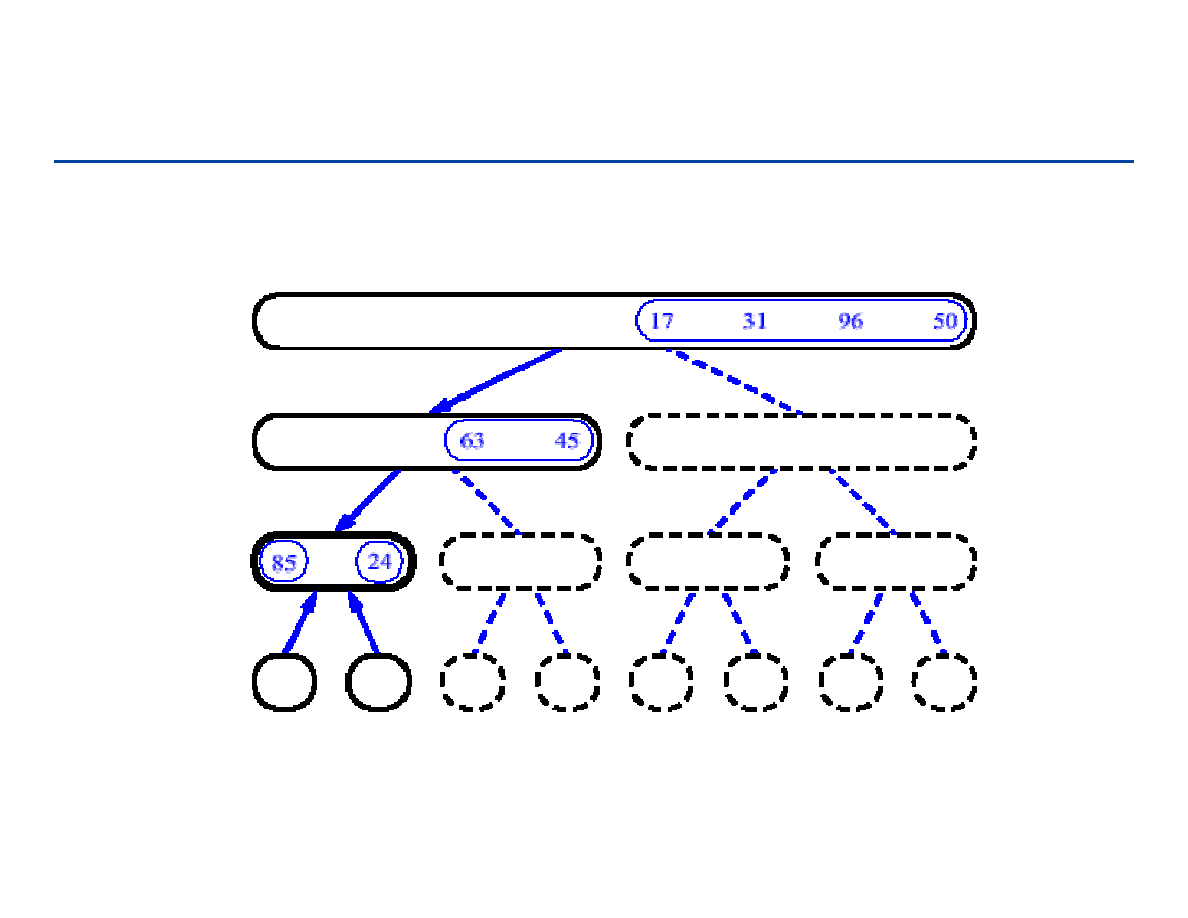
Sortowanie przez łączenie - 7

70

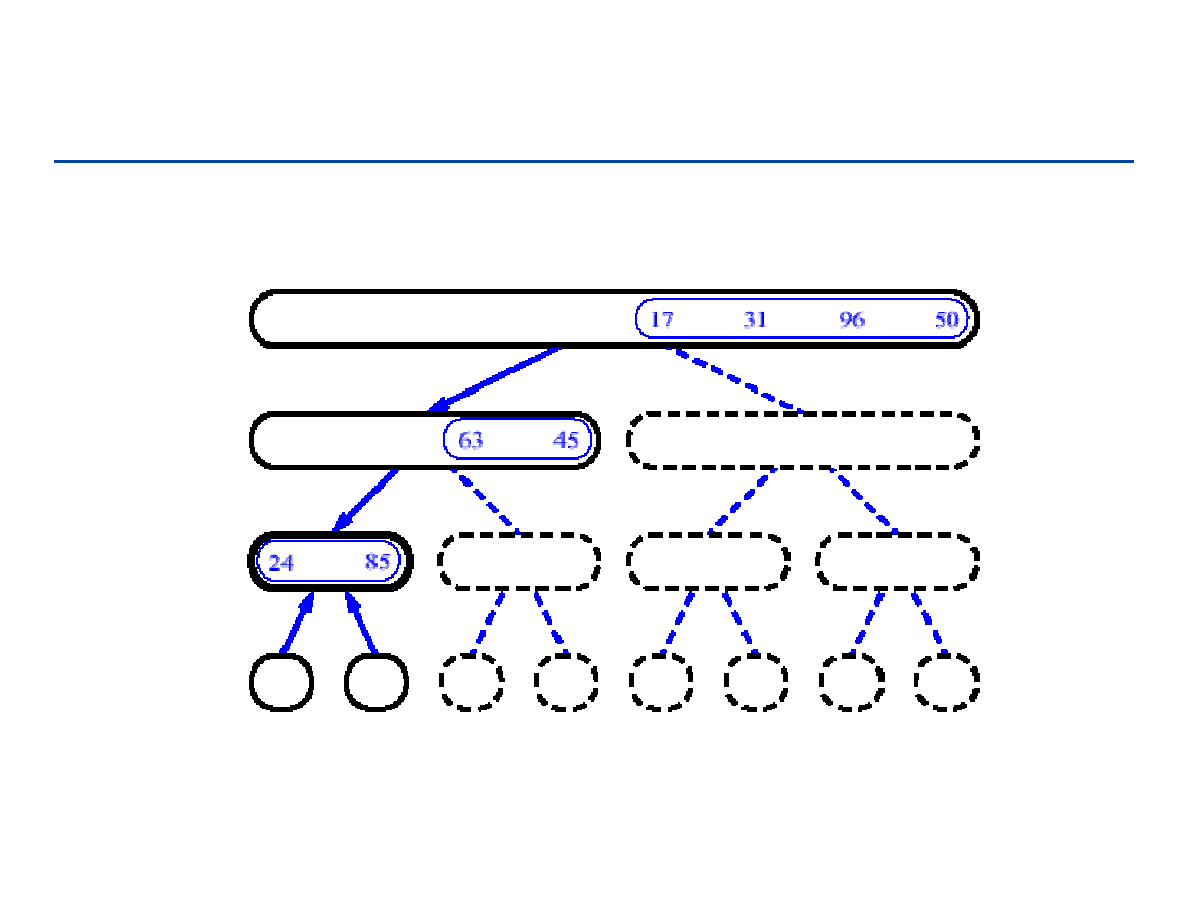
Sortowanie przez łączenie - 8

71

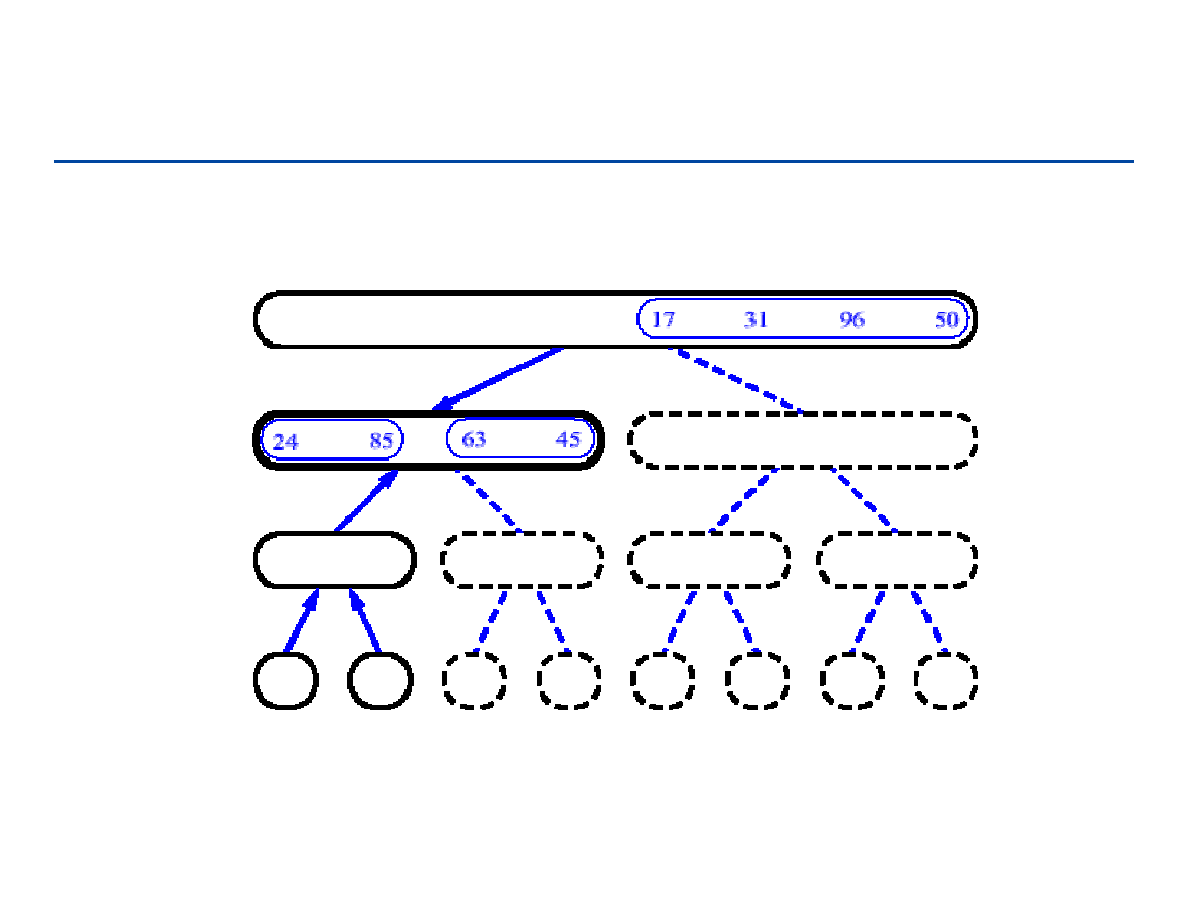
Sortowanie przez łączenie - 9

72

Sortowanie przez łączenie - 10

73

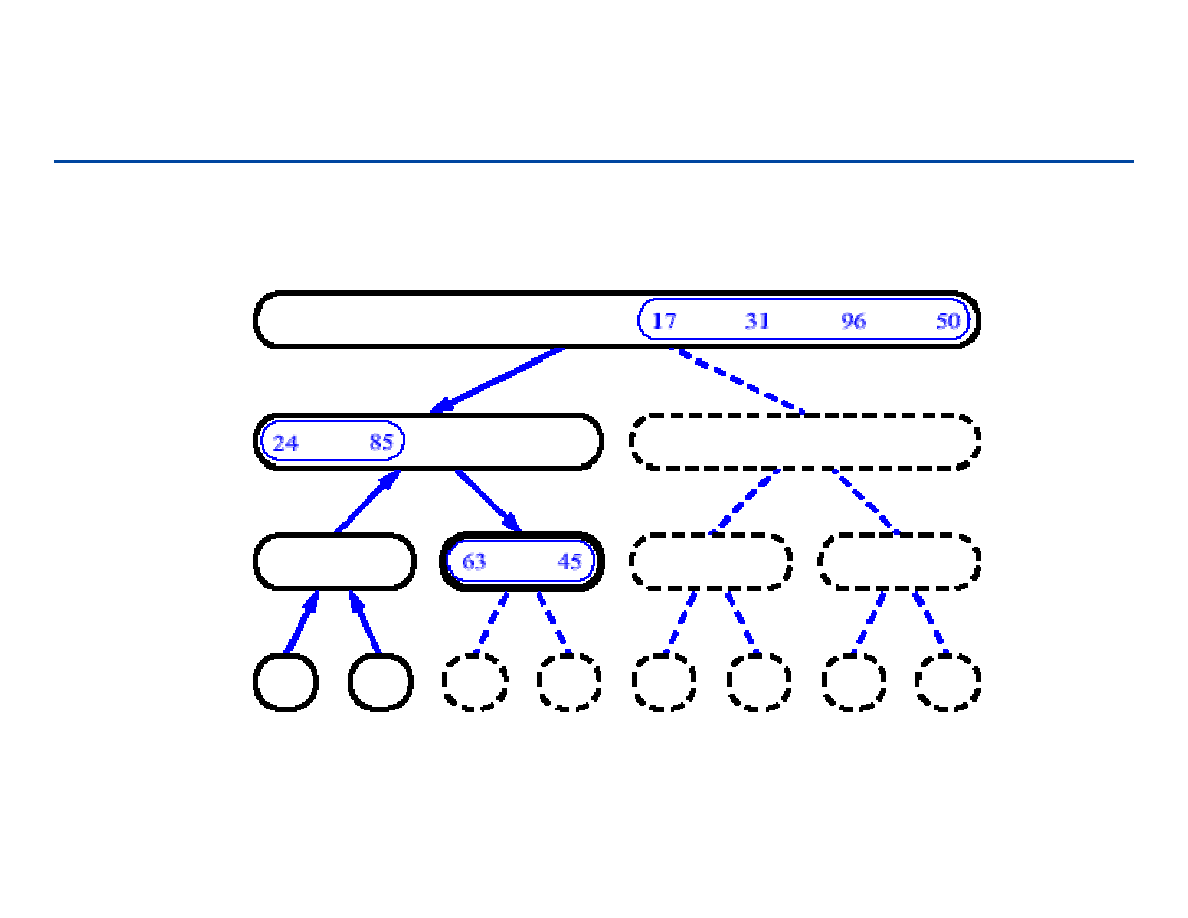
Sortowanie przez łączenie - 11

74

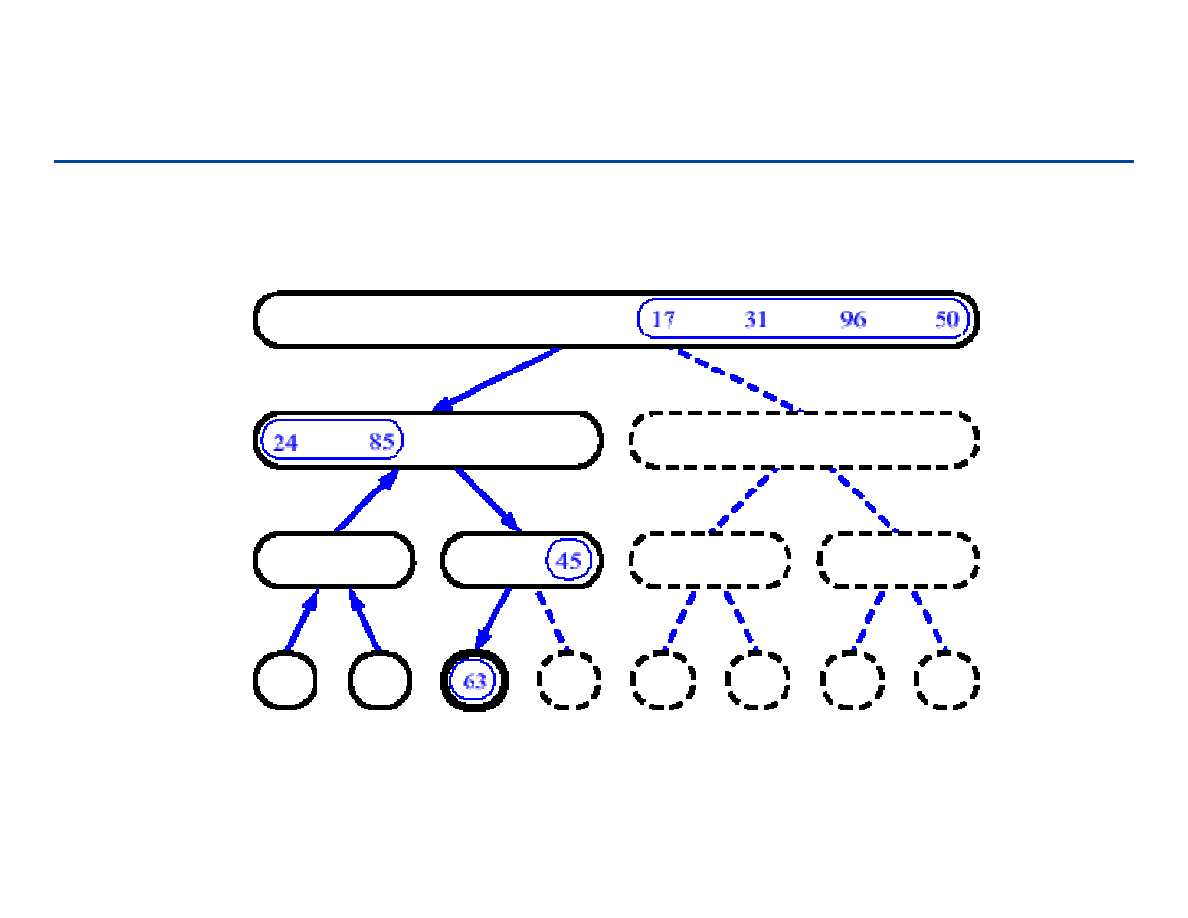
Sortowanie przez łączenie - 12

75

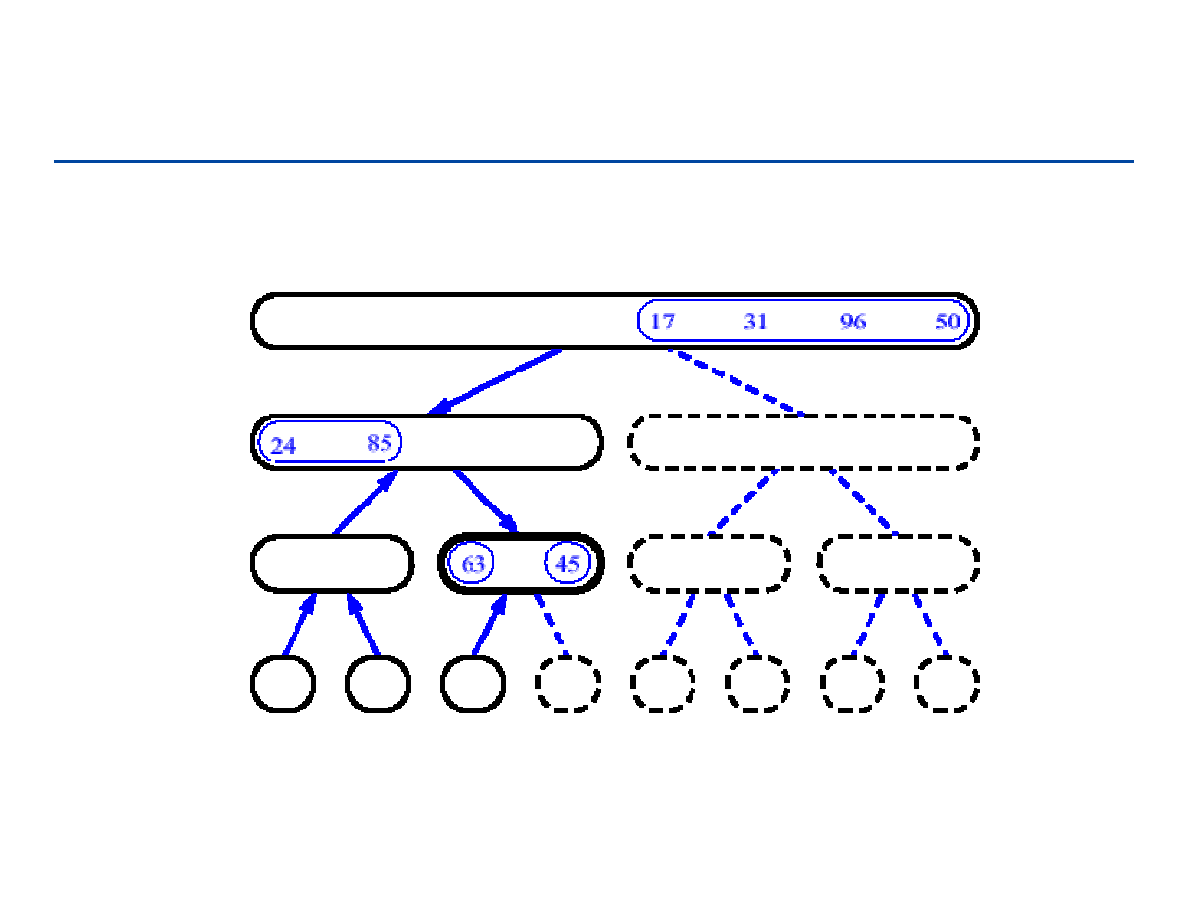
Sortowanie przez łączenie - 13

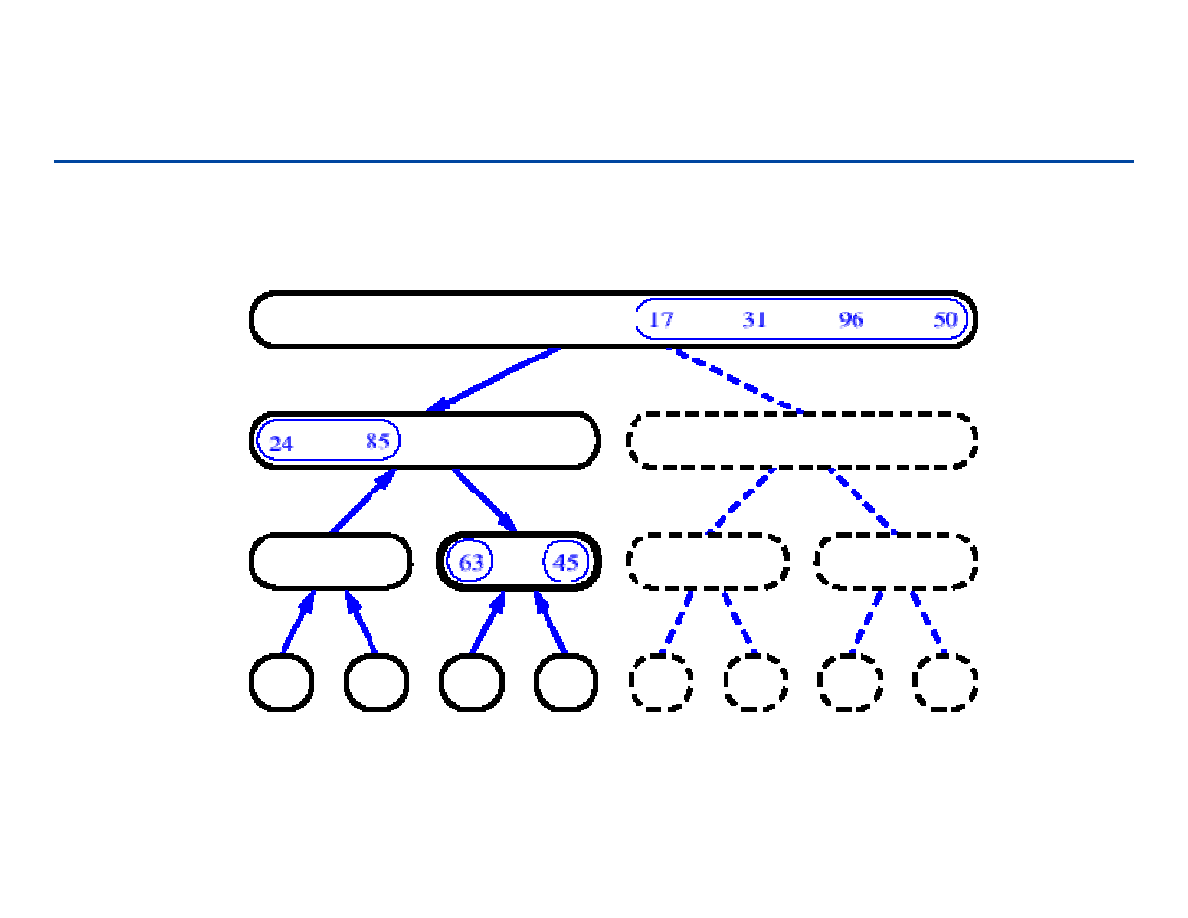
76

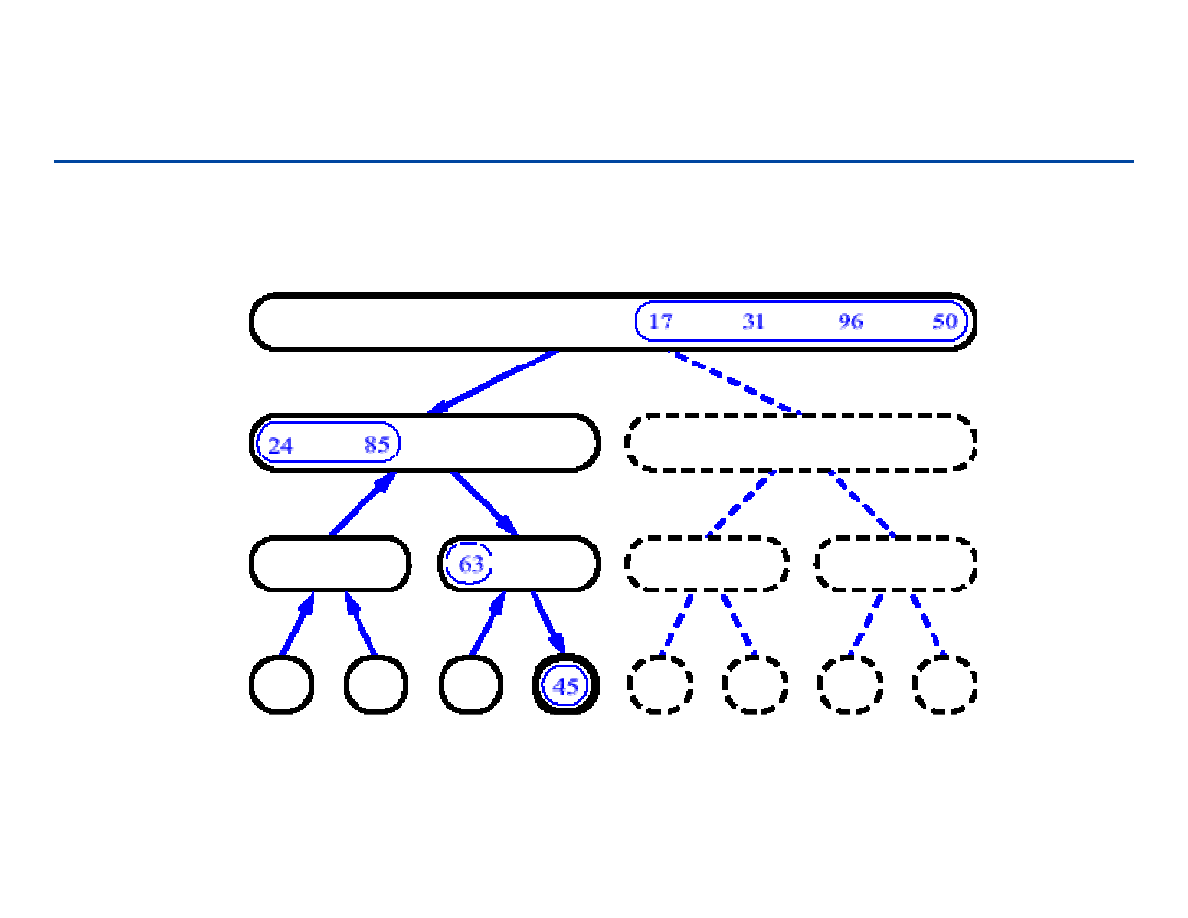
Sortowanie przez łączenie - 14

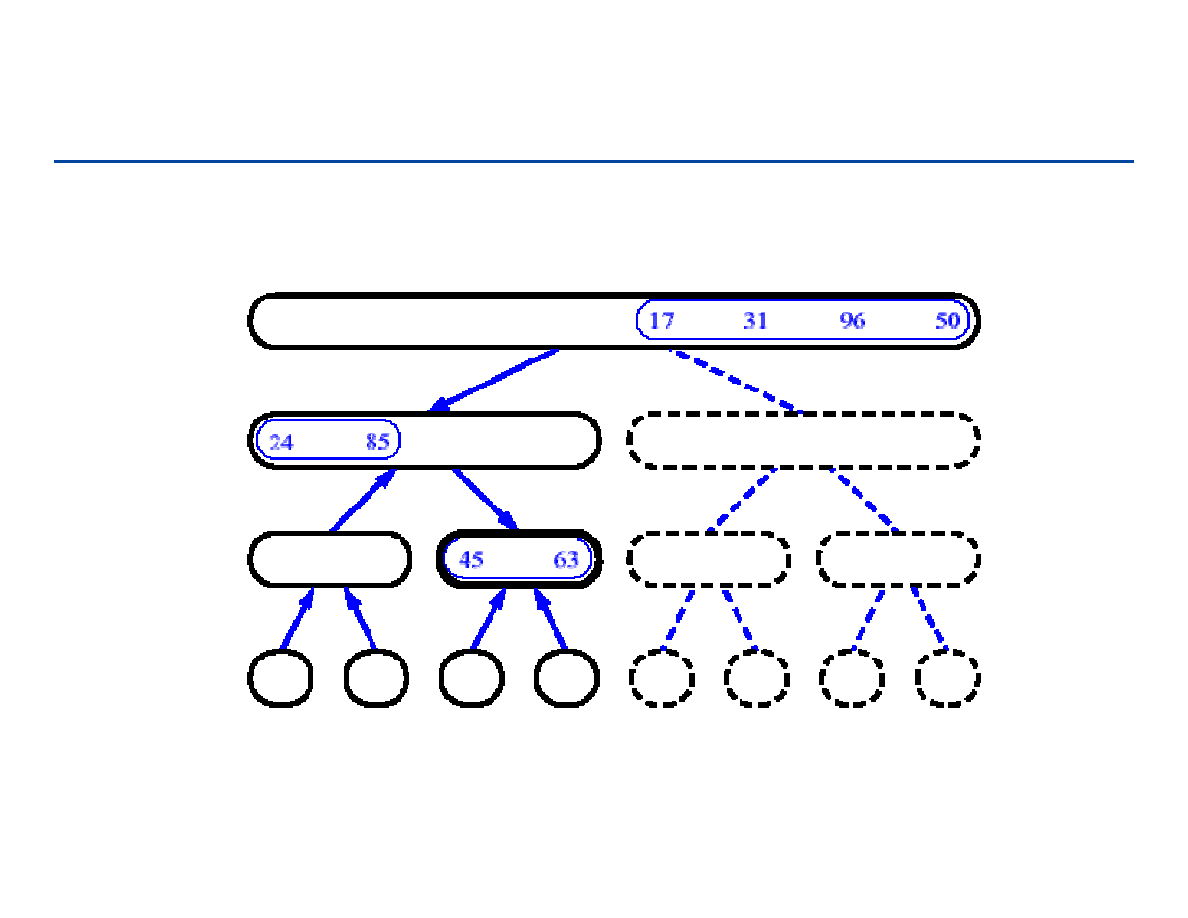
77

Sortowanie przez łączenie - 15

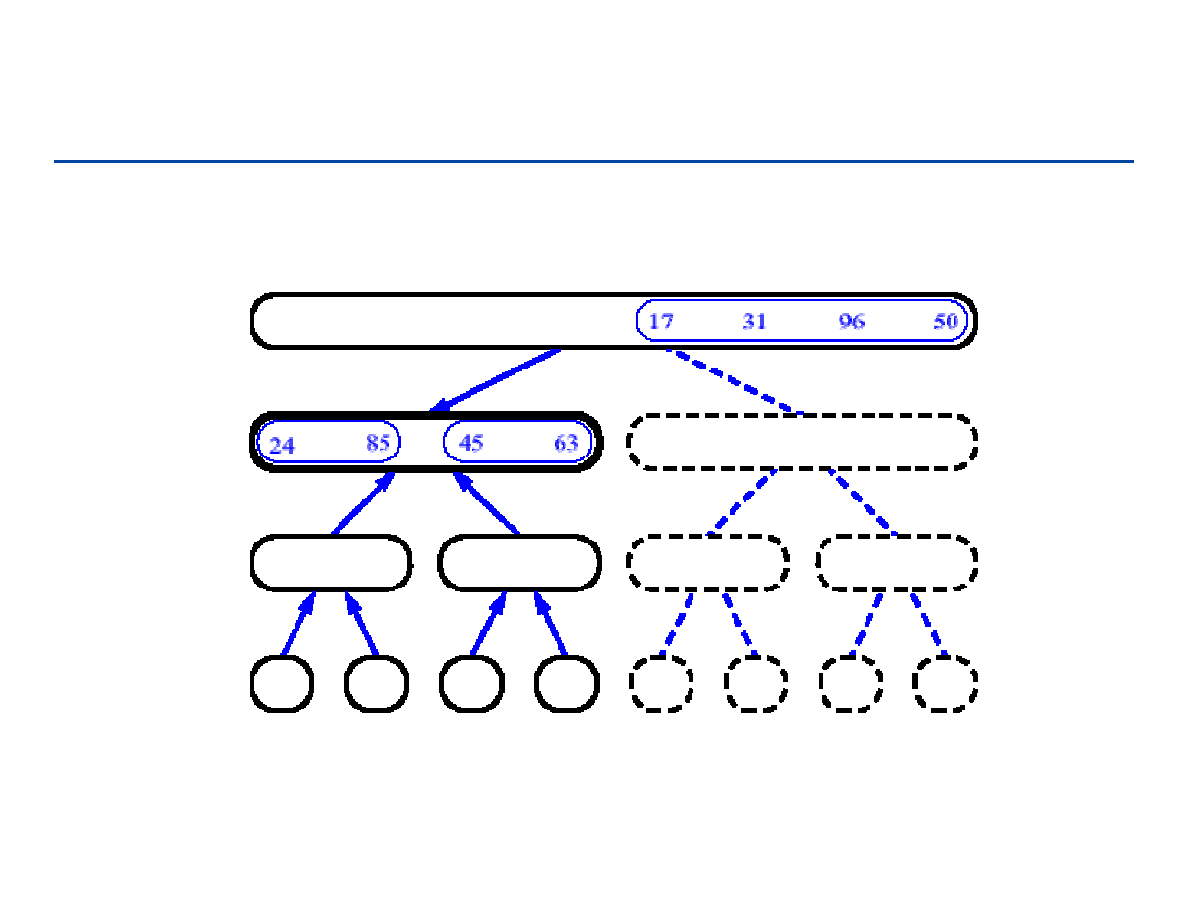
78

Sortowanie przez łączenie - 16

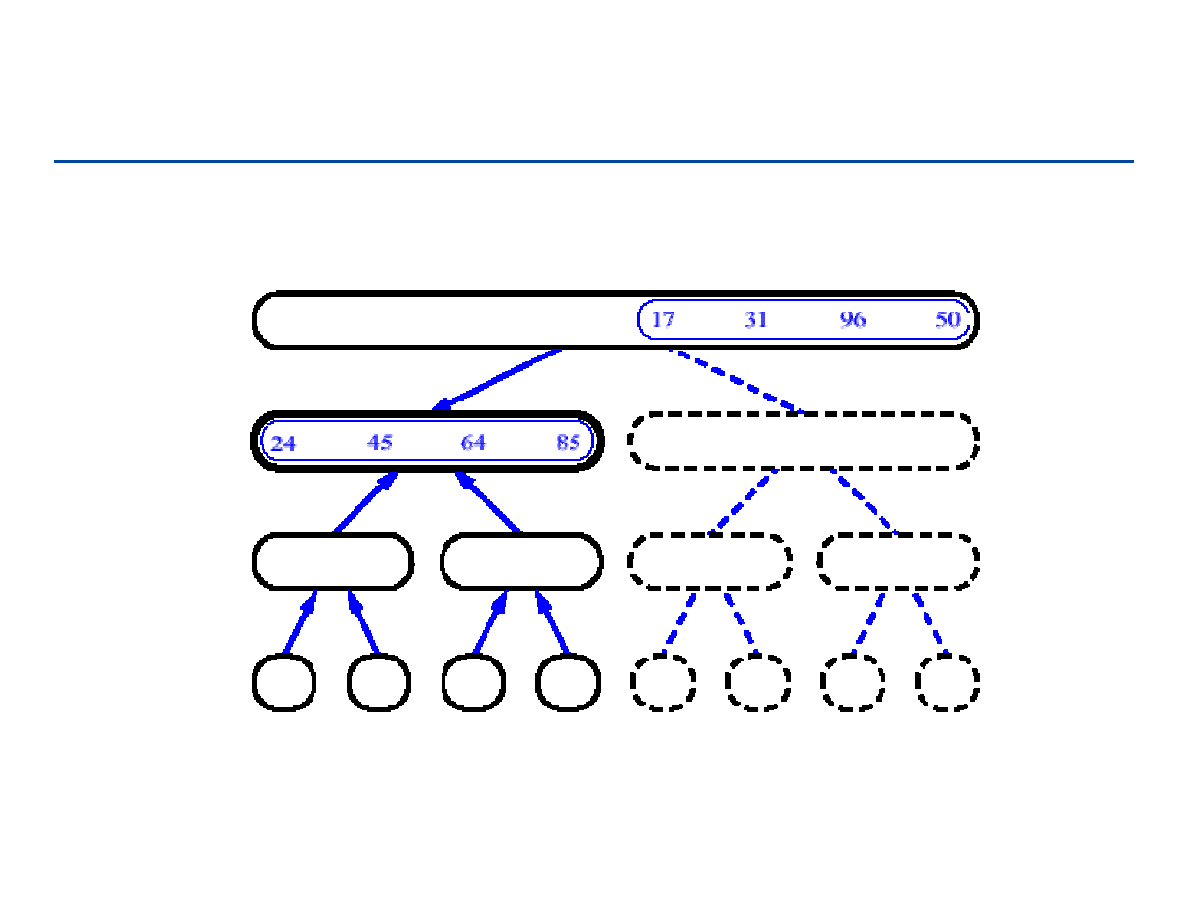
79

Sortowanie przez łączenie - 17

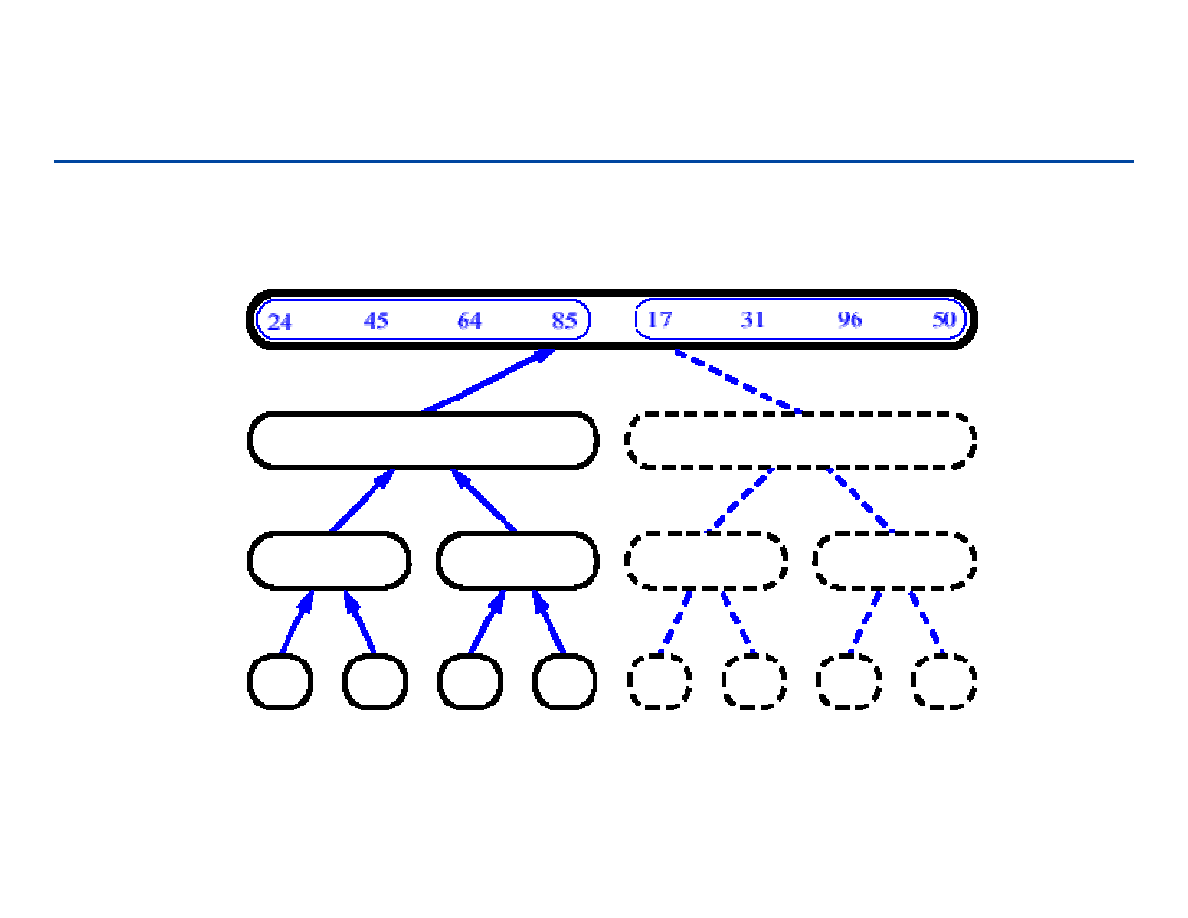
80

Sortowanie przez łączenie - 18

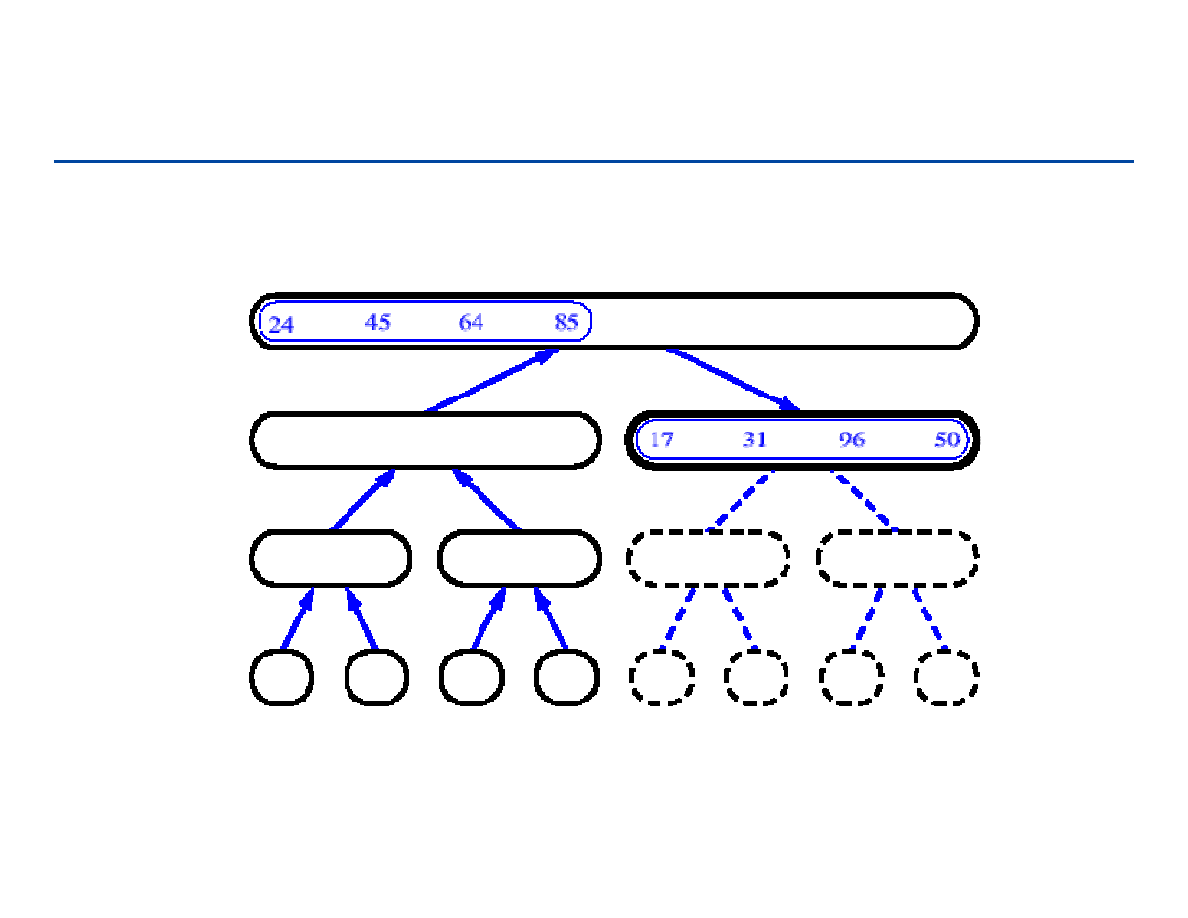
81

Sortowanie przez łączenie - 19

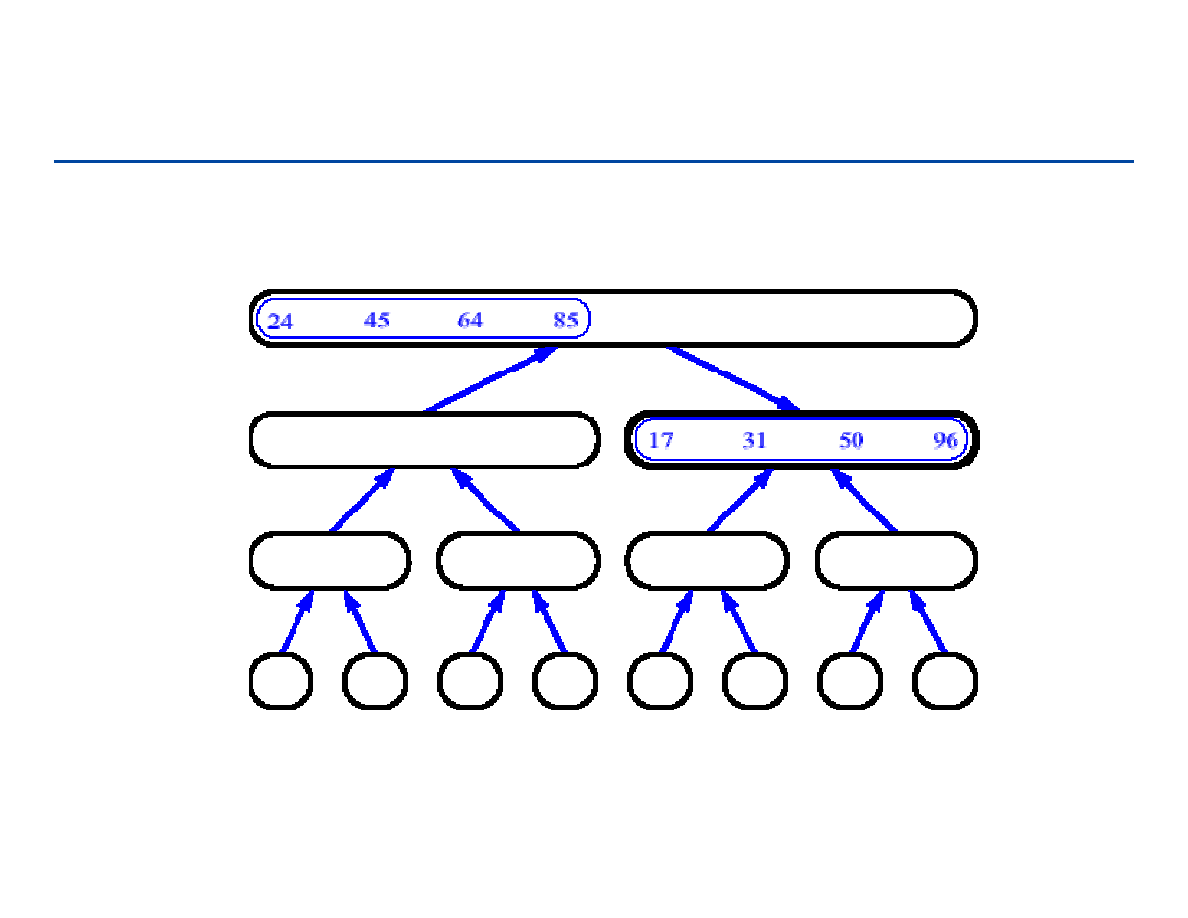
82

Sortowanie przez łączenie - 20

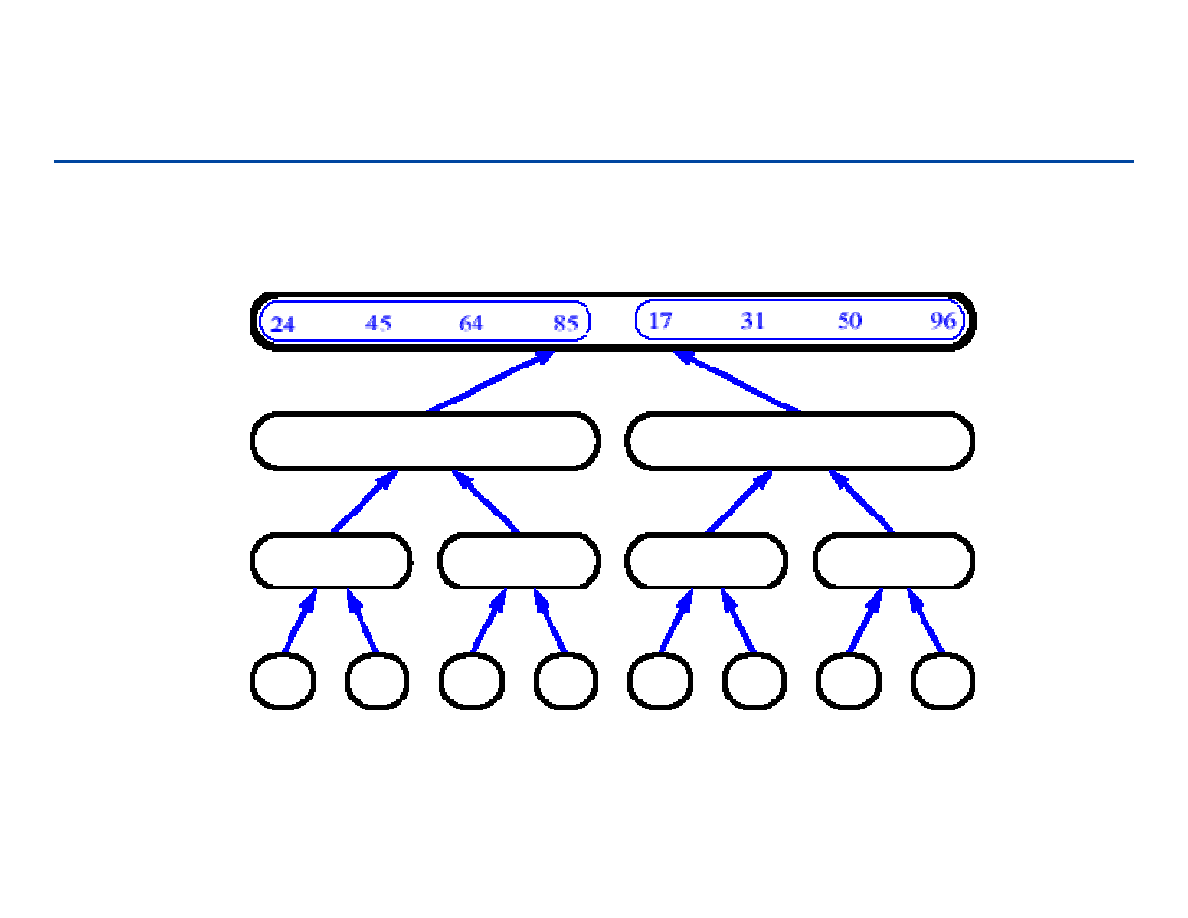
83

Sortowanie przez łączenie - 21

84

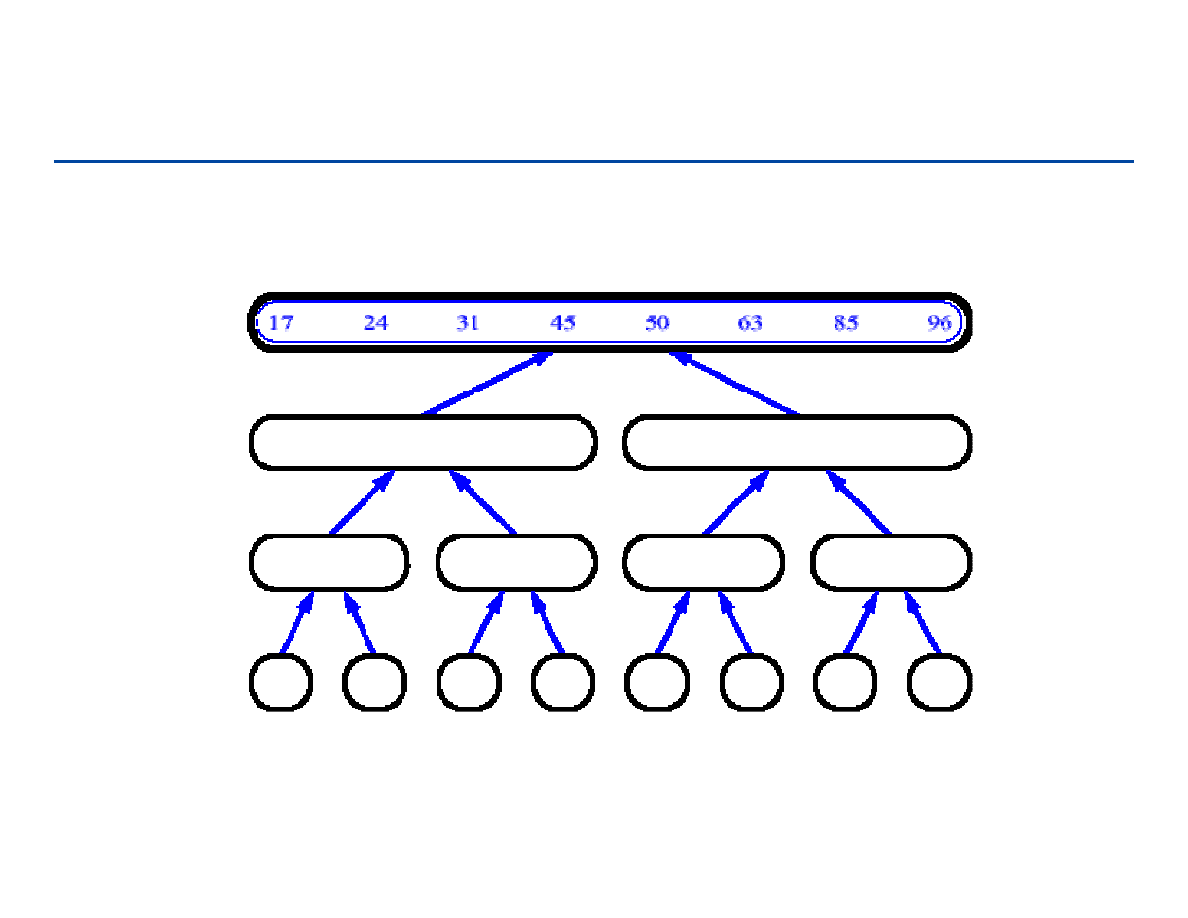
Sortowanie przez łączenie - 22

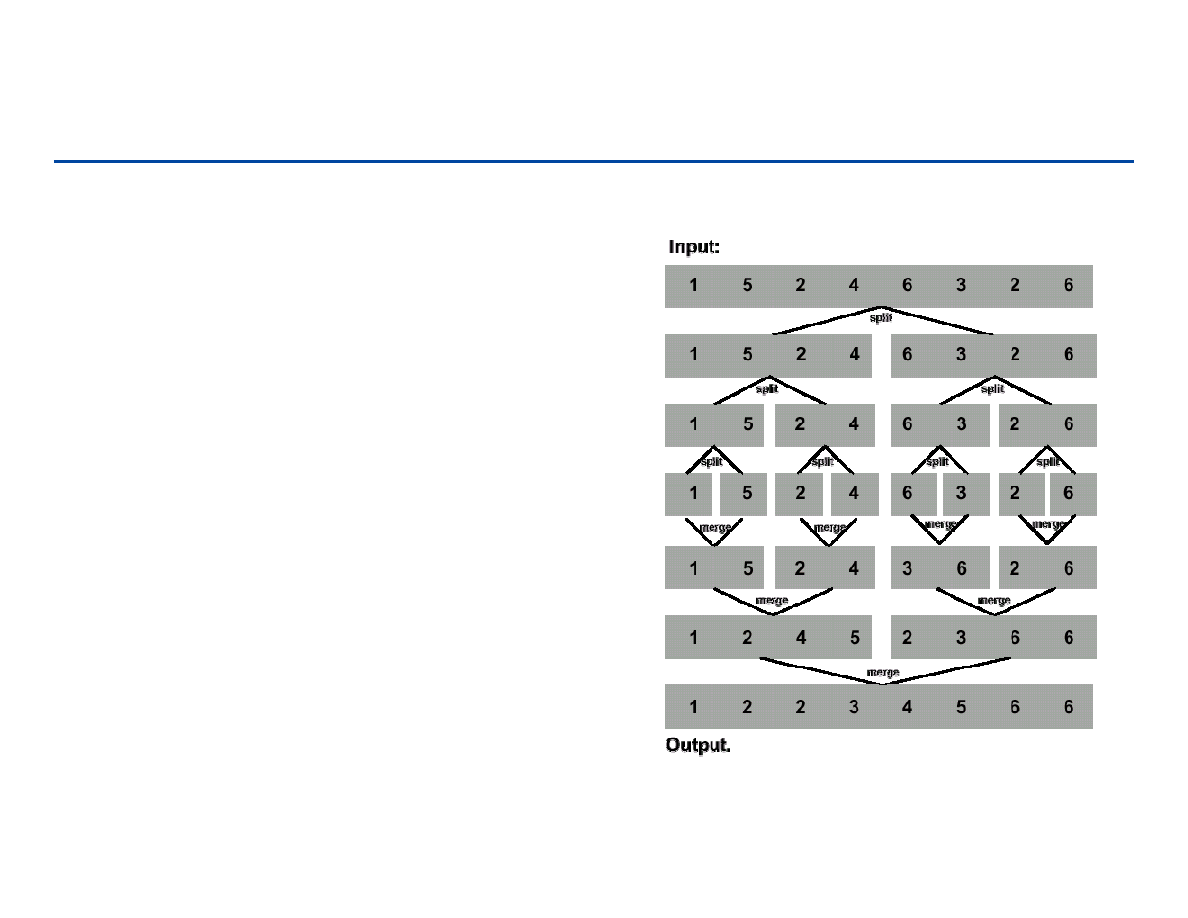
85

Sortowanie przez łączenie – podsumowanie

Sortowanie n liczb

– jeśli n=1 – trywialne

– rekursywnie sortujemy 2 ciągi n/2 i

n/2 liczb

– łączymy dwa ciągi w czasie Θ(n)

Strategia

– Podział problemu na mniejsze, ale

analogiczne podproblemy

– Rekursywne rozwiązywanie

podproblemów

– Łączenie otrzymanych rozwiązań

86

Sortowanie przez łączenie – czas działania

Czas działania algorytmu może być

reprezentowany przez następującą
zależność rekurencyjną:

Po rozwiązaniu dostajemy:

(1)

if

1

( )

2 ( / 2)

( ) if

1

n

T n

T n

n

n

Θ

=



=



+ Θ

>



)

lg

(

)

(

n

n

n

T

Θ

=

87

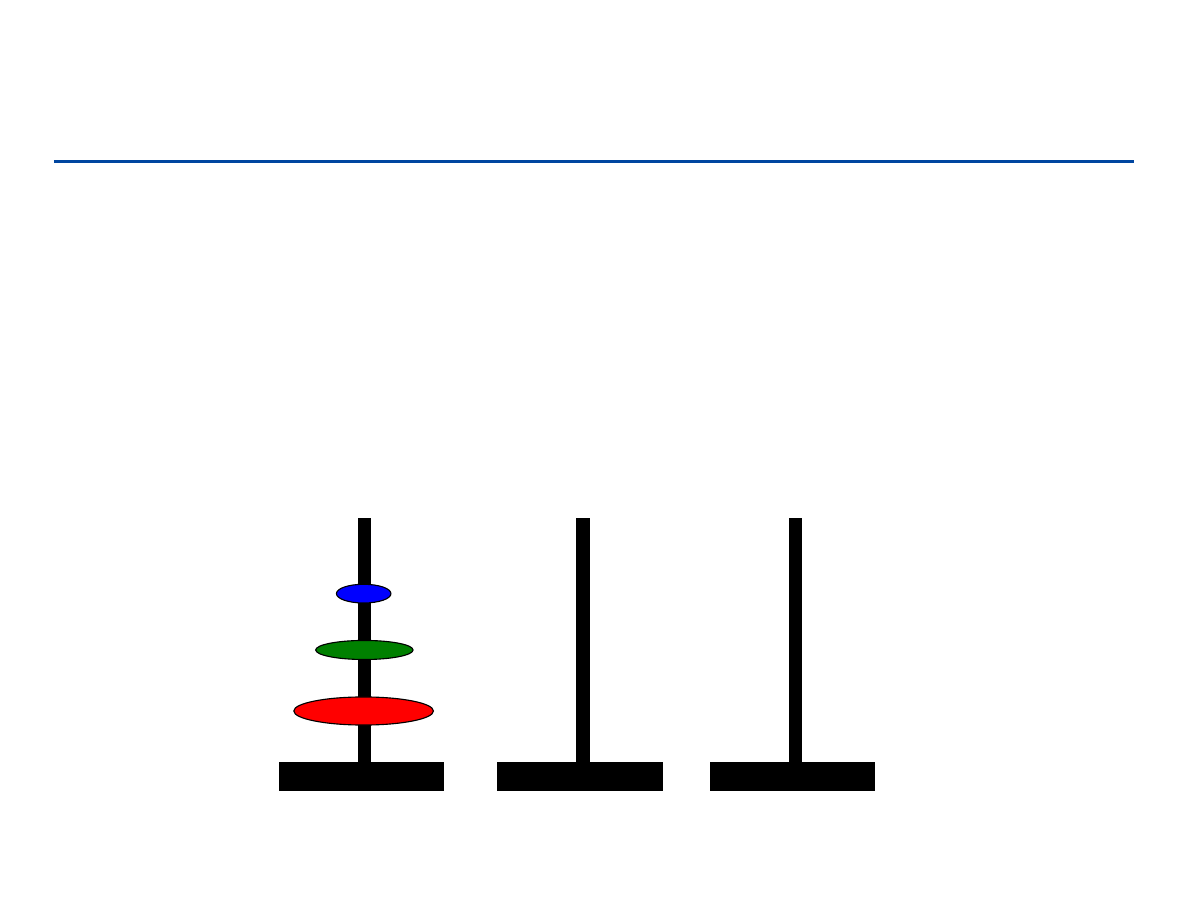
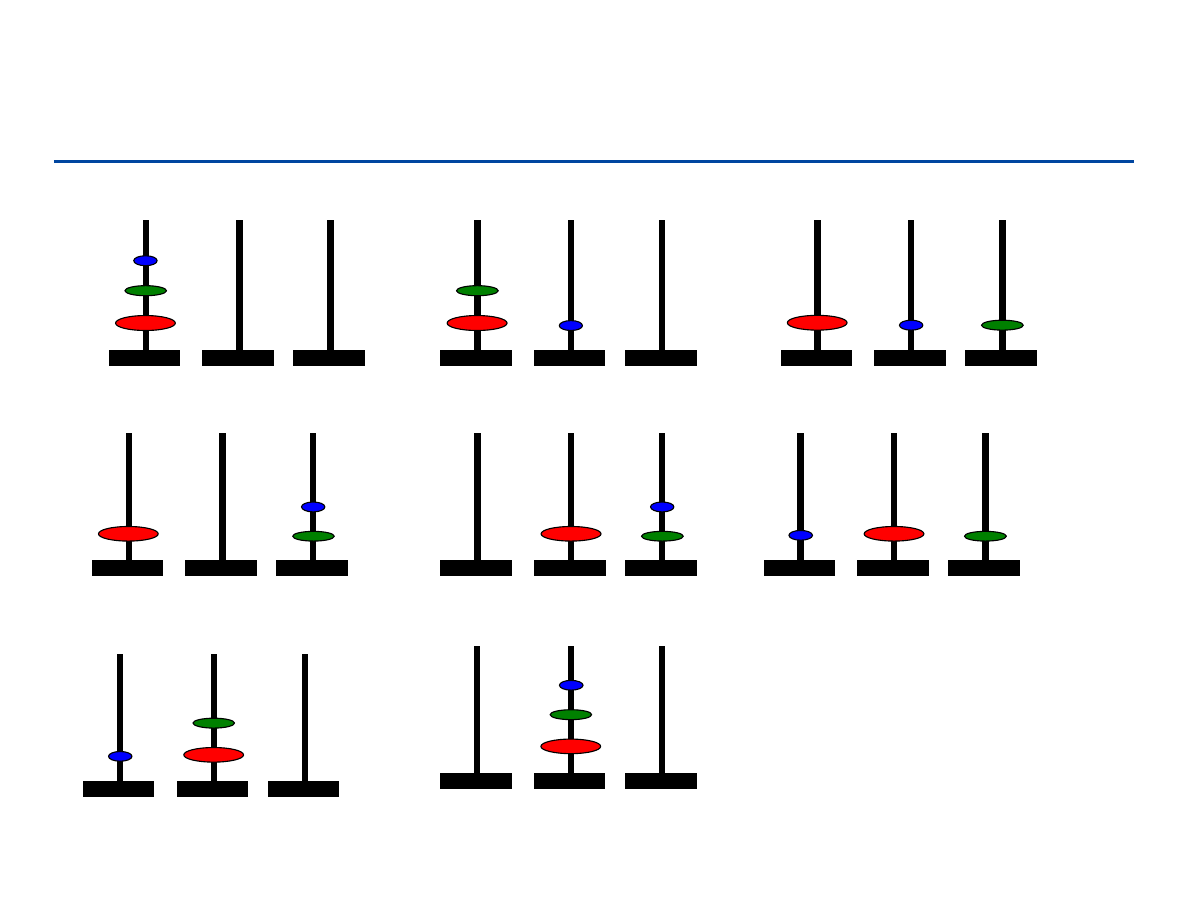
Wieże Hanoi

Mamy 3 wieże oraz stos 64 dysków o zmniejszających się średnicach

umieszczonych na pierwszej wieży

Potrzebujemy przenieść wszystkie dyski na inną wieżę

Zabronione jest położenie dysku większego na mniejszym

W każdym kroku wolno mam przenieść tylko jeden dysk

88

Wieże Hanoi

89

Rozwiązanie rekursywne

90

Algorytm rekursywny

INPUT: n – ilość dysków , a, b, c – wieże, wieża a zawiera wszystkie dyski.
OUTPUT: a, b, c – wieże, wieża b zawiera wszystkie dyski

Hanoi

(n, a, b, c)

if

n = 1 then

Move

(a,b);

else

Hanoi

(n-1,a,c,b);

Move

(a,b);

Hanoi

(n-1,c,b,a);

INPUT: n – ilość dysków , a, b, c – wieże, wieża a zawiera wszystkie dyski.
OUTPUT: a, b, c – wieże, wieża b zawiera wszystkie dyski

Hanoi

(n, a, b, c)

if

n = 1 then

Move

(a,b);

else

Hanoi

(n-1,a,c,b);

Move

(a,b);

Hanoi

(n-1,c,b,a);

Poprawność algorytmu łatwo pokazać przez indukcję względem n.

91

Ilość kroków

Ilość kroków M(n) potrzebnych do

rozwiązania problemu dla n dysków

spełnia zależność rekurencyjną

M(1) = 1

M(n) = 2M(n-1) + 1

15

4

31

5

7

3

3

2

1

1

M(n)

n

92

Ilość kroków

Rozwijając tę zależność dostajemy

M(n) = 2M(n-1) + 1

= 2*[2*M(n-2)+1] + 1 = 2

2

* M(n-2) + 1+2

= 2

2

* [2*M(n-3)+1] + 1 + 2

= 2

3

* M(n-3) + 1+2 + 2

2

=…

Po k krokach

M(n) = 2

k

* M(n-k) + 1+2 + 2

2

+ … + 2

n-k-1

Dla k = n-1

M(n) = 2

n-1

* M(1) + 1+2 + 2

2

+ … + 2

n-2

= 1 + 2 + … + 2

n-1

= 2

n

-1

93

Sortowanie

94

Sortowanie - zadanie

Definicja (dla liczb):

wejście: ciąg n liczb A = (a

1

, a

2

, …, a

n

)

wyjście: permutacja (a

1

,…, a’

n

) taka, że a’

1

≤

… ≤ a’

n

Po co sortować?

– Podstawowy problem dla algorytmiki

– Wiele algorytmów wykorzystuje sortowanie jako procedurę pomocniczą

– Pozwala pokazać wiele technik

– Dobrze zbadane (czas)

95

Sortowanie – taksonomia

Wewnętrzne i zewnętrzne

– Zależnie od miejsca przechowywania zbioru: (RAM czy dysk)

Sortowanie tablic i sortowanie list łączonych

– zależnie od struktury danych (pliku);

– różny sposób dostępu (bezpośredni dla tablicy, sekwencyjny dla listy).

„W miejscu” lub nie

– Nie wymaga dodatkowej pamięci

Stabilne i niestabilne

– Kolejność elementów o tych samych wartościach klucza nie zmienia się.

Inaczej kolejne sortowanie dla złożonych obiektów nie psuje efektów

poprzedniego sortowania.

Bezpośrednie i pośrednie

– zależnie od tego przemieszczamy całe obiekty, czy tylko wskaźniki

(indeksy) do nich

96

Zestawienie czasów działania

Przez wybór: O(N

2

) zawsze

Bąbelkowe: O(N

2

) najgorszy przypadek; O(N) najlepszy przyp.

Wstawianie: O(N

2

) średnio; O(N) najlepszy przypadek

Shellsort:

O(N

4/3

)

Heapsort:

O(NlogN) zawsze

Mergesort:

O(NlogN) zawsze

Quicksort:

O(NlogN) średnio; O(N

2

) najgorszy przypadek

Zliczanie:

O(N) zawsze

Radix sort:

O(N) zawsze

zewnętrzne: O(b logb)) dla pliku o b „stronach”.

97

Sortowanie przez wybór – pomysł

Znajdujemy najmniejszy element ciągu i zamieniamy go z

pierwszym elementem. Powtarzamy to dla podciągu bez

pierwszego elementu, itd.

Znajdź minimum i zamień
z pierwszym elementem

X

X

98

Sortowanie przez wybór – pseudokod

Selection_Sort(int A)

1

for i ← 1 to length[A]

2

do min ← i;

3

for j ← i+1 to length[A]

4

do if A[j] < A[min] then min ← j;

5 Exchange A[min] ↔ A[i]

99

ciąg: EASYQUESTION - rozmiar 12 znaków

#porównań

#zamian

EASYQUESTION

A

ESYQUESTION

11

1

AE

SYQUESTION

10

1

AEE

YQUSSTION

9

1

AEEI

QUSSTYON

8

1

AEEIN

USSTYOQ

7

1

AEEINO

SSTYUQ

6

1

AEEINOQ

STYUS

5

1

AEEINOQS

TYUS

4

1

AEEINOQSS

YUT

3

1

AEEINOQSST

UY

2

1

AEEINOQSSTU

Y

1

1

Razem

66 11

1
2
3
4
5
6
7
8
9

10
11

Sortowanie przez wybór – przykład

iteracja

100

Sortowanie przez wybór – czas działania

Zależność od danych wejściowych:

– Ilość przebiegów: nie (zawsze N-1)

– Ilość porównań: nie

– Ilość zamian: nie

O(N

2

) zawsze (bez znaczenia jaki jest układ elementów w danych –

ważna tylko ilość)

101

Sortowanie bąbelkowe (przez zamianę)

Przechodzimy przez ciąg od jego końca, porównując sąsiadujące

elementy i ewentualnie zamieniając je miejscami. Powtarzamy te
procedurę aż do uporządkowania całego ciągu.

– Po pierwszym przejściu element minimalny znajduje się na

początku – a[0], po drugim na drugim miejscu znajduje się drugi co

do wielkości – a[1], po itd.

Porównanie do wypływających

bąbelków – stąd nazwa

.

102

Sortowanie bąbelkowe – pseudokod

BUBBLE_SORT(A)

1

for i ← 1 to length[A]

2

do for j ← length[A] downto i + 1

3

do if A[j] < A[j - 1]

4

then exchange A[j] ↔ A[j - 1]

103

Ciąg: EASYQUESTION, (12 znaków)

porównań

zamian

EASYQUESTION

(najgorszy przyp)

A

EESYQUISTNO

11 (11)

8 (11)

AE

EISYQUNSTO

10 (10)

6 (10)

AEE

INSYQUOST

9 (9)

6 (9)

AEEI

NOSYQUST

8 (8)

4 (8)

AEEIN

OQSYSUT

7 (7)

3 (7)

AEEINO

QSSYTU

6 (6)

2 (6)

AEEINOQ

SSTYU

5 (5)

1 (5)

AEEINOQS

STUY

4 (4)

1 (4)

AEEINOQS

STUY

3 (3)

0

(3)

(2)

(2)

(1)

(1)

razem

63 (66)

31 (66)

iteracja

1

2
3
4
5
6
7
8
9

Sortowanie bąbelkowe – przykład

104

Sortowanie bąbelkowe – czas wykonania

Zależność od danych wejściowych:

– Ilość potrzebnych przejść: tak
– Ilość porównań w jednym przejściu: nie
– Ilość zamian: tak

Najgorszy przypadek: O(N

2

)

– Dane odwrotnie posortowane, np.: JIHGFEDCBA.
– N-1 przejść
– (N-1)N/2 porównań i (N-1)N/2 zamian

Najlepszy przypadek: O(N)

– Jeśli elementy są już posortowane, np.: ABCDEFGHIJ.
– Tylko jedno przejście. Stąd mamy N-1 porównań i 0 zamian.

105

Sortowanie przez wstawianie – pomysł

Dla każdego elementu ciągu (od lewej do prawej), wstawiamy go

we właściwe miejsce ciągu elementów poprzedzających go (już

posortowanych).

106

Sortowanie przez wstawianie – pseudokod

INSERTION_SORT(A)

1

for j ← 2 to length[A]

2

do key ← A[j]

3 i ← j-1

4

while i>0 and A[i]>key

5

do A[i+1] ← A[i]

6

i ← i-1

7

A[i+1] ← key

107

Ciąg: EASYQUESTION, (12 znaków)

porównań

zamian

(najgorszy przyp.)

E

ASYQUESTION

A

E

SYQUESTION

1 (1)

1 (1)

AE

S

YQUESTION

1 (2)

0 (2)

AES

Y

QUESTION

1 (3)

0 (3)

AE

Q

SY

UESTION

3 (4)

2 (4)

AEQS

U

Y

ESTION

2 (5)

1 (5)

AE

E

QSUY

STION

5 (6)

4 (6)

AEEQS

S

UY

TION

3 (7)

2 (7)

AEEQSS

T

UY

ION

3 (8)

2 (8)

AEE

I

QSSTUY

ON

7 (9)

6 (9)

AEEI

O

QSSTUY

N

7 (10)

6 (10)

AEEI

N

OQSSTUY

8 (11)

7 (11)

razem

41 (66) 31 (66)

iteracja

1
2
3
4
5
6
7
8
9

10
11

Sortowanie przez wstawianie – przykład

108

Sortowanie przez wstawianie – czas działania

Zależność od danych wejściowych:

– Ilość iteracji: nie (zawsze N-1)

– Ilość porównań: tak

– Ilość zamian: tak

Najgorszy przypadek: O(N

2

)

– Elementy odwrotnie posortowane np.: JIHGFEDCBA.

– (N-1)N/2 porównań i (N-1)N/2 zamian.

Najlepszy przypadek: O(N)

– Elementy już posortowane np.: ABCDEFGHIJ.

– Jedno porównanie i 0 zamian w każdej iteracji. Razem, N-1

porównań i brak zamian.

109

Shellsort – pomysł

Modyfikacja (rozszerzona wersja) sortowania przez wstawianie

Dążymy do zmniejszenia ilości zamian – albo ciągi krótkie, albo

lepsze („bliższe” posortowania).

Shellsort wykonuje sortowanie podciągów:

– Wybieramy ciąg liczb (zwany ciągiem przyrostów) h

t

, … , h

2

, h

1

;

– h

1

=1; h

t

> … > h

2

>h

1

;

– Sortujemy ciągi elementów odległych o h

t

, h

t-1

, h

t-2

,…,h

1

.

110

Shellsort – kod w C

void shellsort (int[ ] a, int n)
{

int i, j, k, h, v;
int[ ] cols = {1391376, 463792, 198768, 86961, 33936, 13776, 4592, 1968, 861,

336, 112, 48, 21, 7, 3, 1}

for (k=0; k<16; k++)

{

h=cols[k];
for (i=h; i<n; i++)

{

v=a[i];
j=i;
while (j>=h && a[j-h]>v)

{

a[j]=a[j-h];
j=j-h;

}

a[j]=v;

}

}

}

111

Shellsort – przykład

ciąg: EASYQUESTION (12 znaków)
ciąg przyrostów 4, 1.

porównań

zamian

EASYQUESTION

E

ASY

Q

UES

T

ION

2

0

E

A

SY

Q

I

ES

T

U

ON

3

1

E

A

E

Y

Q

I

O

S

T

U

S

N

3

2

E

A

E

N

Q

I

O

S

T

U

S

Y

3

3

Razem w tej fazie

11

6

faza 1: przyrost = 4

112

Shellsort – przykład

porównań

zamian

EAENQIOSTUSY

AE

ENQIOSTUSY

1

1

AEE

NQIOSTUSY

1

0

AEEN

QIOSTUSY

1

0

AEENQ

IOSTUSY

1

0

AEEINQ

OSTUSY

3

2

AEEINOQ

STUSY

2

1

AEEINOQS

TUSY

1

0

AEEINOQST

USY

1

0

AEEINOQSTU

SY

1

0

AEEINOQSSTU

Y

3

2

AEEINOQSSTUY

1

0

Razem w tej fazie

16

6

faza 2: przyrost= 1

113

Shellsort – przykład

Razem 27 porównań i 12 zamian.

Dla sortowania przez wstawiania odpowiednio 41 i 31 !!!

– Polepszenie dostajemy przez wstępne posortowanie, krótkich

podciągów

Zwykle stosuje się ciągi przyrostów o więcej niż 2 elementach.

114

Shellsort – czas działania

Nie ma możliwości przeprowadzenie dokładnej analizy dla przypadki

ogólnego (wyniki są oparte o badania empiryczne).

Wybór ciągu przyrostów ma zasadniczy wpływ na czas sortowania.

– Dla ciągu podanego przez Shell’a: O(N

2

)

• I

max

= Floor(N/2), I

k

= Floor(I

k+1

/2).

• np N=64:1, 2, 4, 8, 16, 32

– Dla ciągu podanego przez Knuth’a: O(N

3/2

)

• I

1

=1, I

k+1

= 1+3*I

k

.

• 1, 4, 13, 40, 121, 364, …

115

Mergesort – pomysł

Dzielimy ciąg na podciągi, sortujemy te podciągi, a następnie

łączymy zachowując porządek.

– Przykład algorytmu typu „dziel i zwyciężaj”.

– Potrzeba dodatkowego miejsca dla tych podciągów – nie jest to

sortowanie „w miejscu”.

• Można realizować ten proces „w miejscu”, ale rośnie stopień

komplikacji.

116

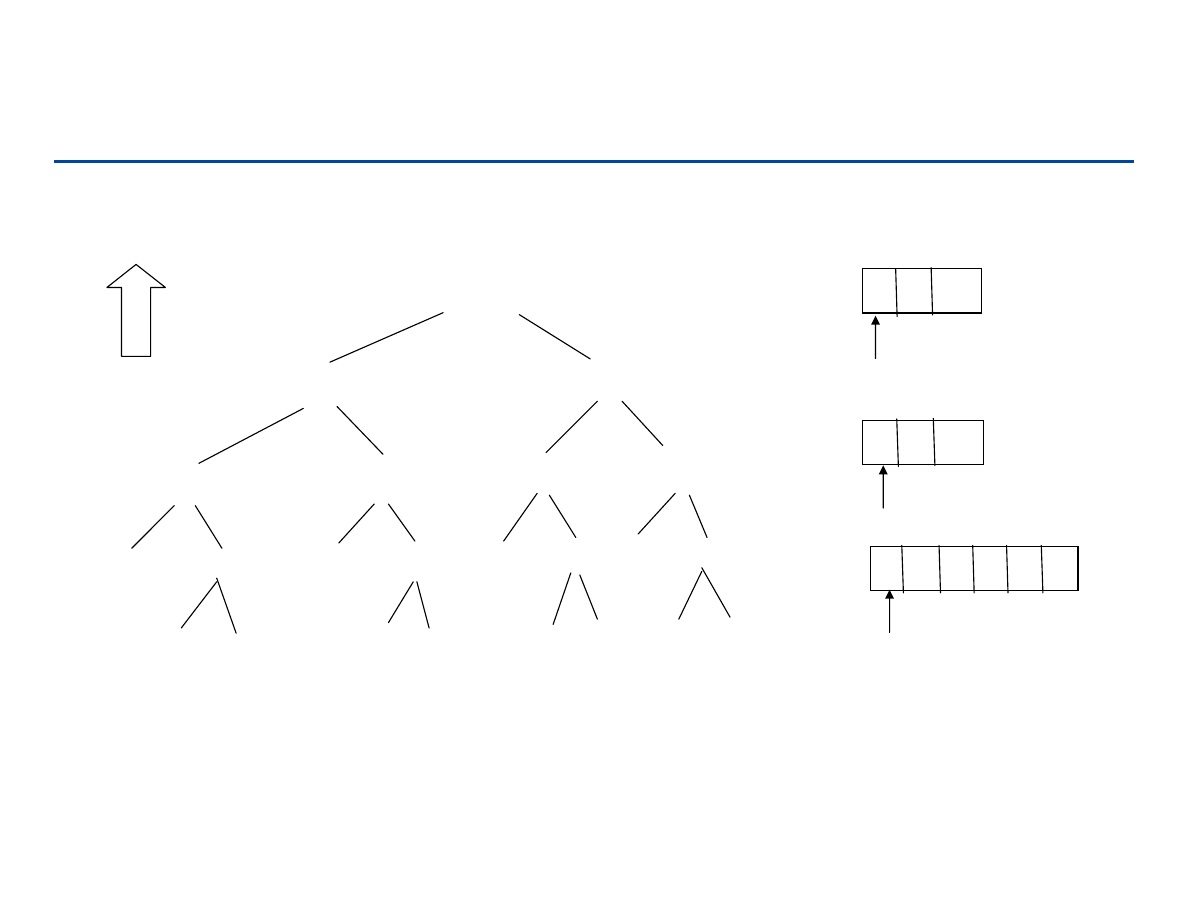
Mergesort – przykład

ciąg: EASYQUESTION (12 znaków)

EASYQUESTION

EASYQU

ESTION

EAS

YQU

EST

ION

E

AS

Y

QU

E

ST

I

ON

A S

Q U

S T

O N

podział

117

Mergesort – przykład

AEEINOQSSTUY

AEQSUY

EINOST

AES

QUY

EST

INO

E

AS

Y

QU

E

ST

I

NO

A S

Q U

S T

O N

łaczenie

A E S

Q U Y

C1

C2

C3

118

Mergesort - pseudokod

MERGE-SORT(A, p, r)

1

if p < r

2

then q ← (p + r)/2

3

MERGE-SORT(A, p, q)

4

MERGE-SORT(A, q + 1, r)

5

MERGE(A, p, q, r)

119

Mergesort - pseudokod

MERGE(A, p, q, r)
1 n1 ← q - p + 1
2 n2 ← r - q
3 create arrays L[1 ..n1 + 1] and R[1 ..n2 + 1]
4

for i ← 1 to n1

5

do L[i] ← A[p + i - 1]

6

for j ← 1 to n2

7

do R[j] ← A[q + j]

8 L[n1 + 1] ← ∞
9 R[n2 + 1] ← ∞
10 i ← 1
11 j ← 1
12

for k ← p to r

13

do if L[i] ≤ R[j]

14

then A[k] ← L[i]

15

i ← i + 1

16

else A[k] ← R[j]

17

j ← j + 1

120

Sortowanie w czasie liniowym

121

Przegląd

Czy możliwe jest sortowanie w czasie lepszym niż dla metod

porównujących elementy (poprzednio – najlepsze algorytmy dawały

czas O(NlogN))?

Algorytmy o liniowym czasie działania:

– Przez zliczanie (Counting-Sort)

– Radix-Sort

– Kubełkowe (Bucket-sort)

Potrzeba dodatkowych założeń!

122

Sortowanie o czasie liniowym

Możliwe przy dodatkowych informacjach (założeniach) o danych

wejściowych.

Przykłady takich założeń:

– Dane są liczbami całkowitymi z przedziału [0..k] i k = O(n).

– Dane są liczbami wymiernymi z przedziału [0,1) o rozkładzie

jednostajnym na tym przedziale

Trzy algorytmy:

– Counting-Sort

– Radix-Sort

– Bucket-Sort

123

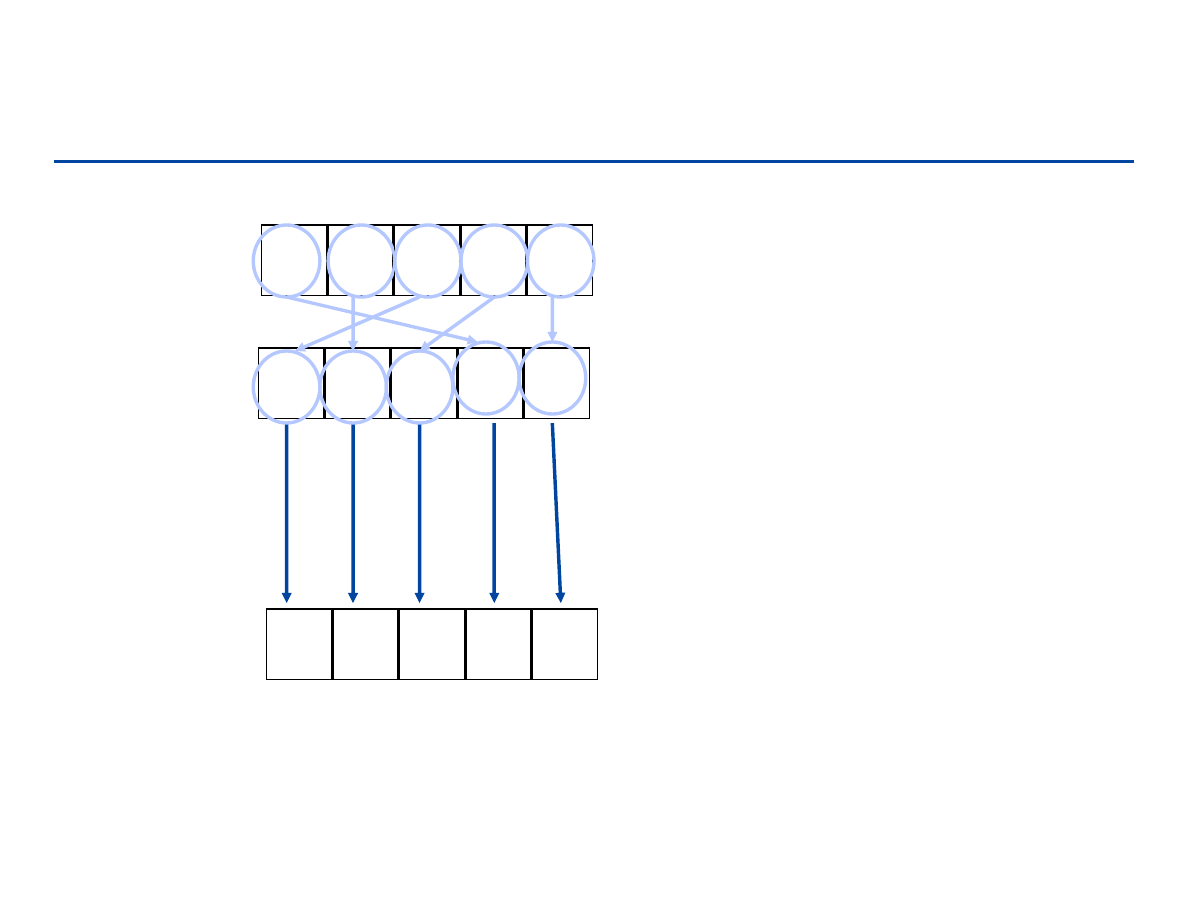
Zliczanie (Counting sort)

wejście: n liczb całkowitych z przedziału [0..k], dla k = O(n).

pomysł: dla każdego elementu wejścia x określamy jego pozycje (rank):

ilość elementów mniejszych od x.

jeśli znamy pozycję elementu – umieszczamy go na r+1 miejscu ciągu

przykład: jeśli wiemy, że w ciągu jest 6 elementów mniejszych od 17, to 17

znajdzie się na 7 miejscu w ciągu wynikowym.

powtórzenia: jeśli mamy kilka równych elementów umieszczamy je kolejno

poczynając od indeksu pozycja

124

Zliczanie (Counting sort)

1

3

2

4

5

Jeśli nie ma powtórzeń i n = k,
Rank[A[i]] = A[i] i B[Rank[A[i]] A[i]

Dla każdego A[i], liczymy elementy

≤

od niego. Daje to rank (pozycję)

elementu

4

1

2

5

A =

B =

Rank =

4

3

5

2

1

3

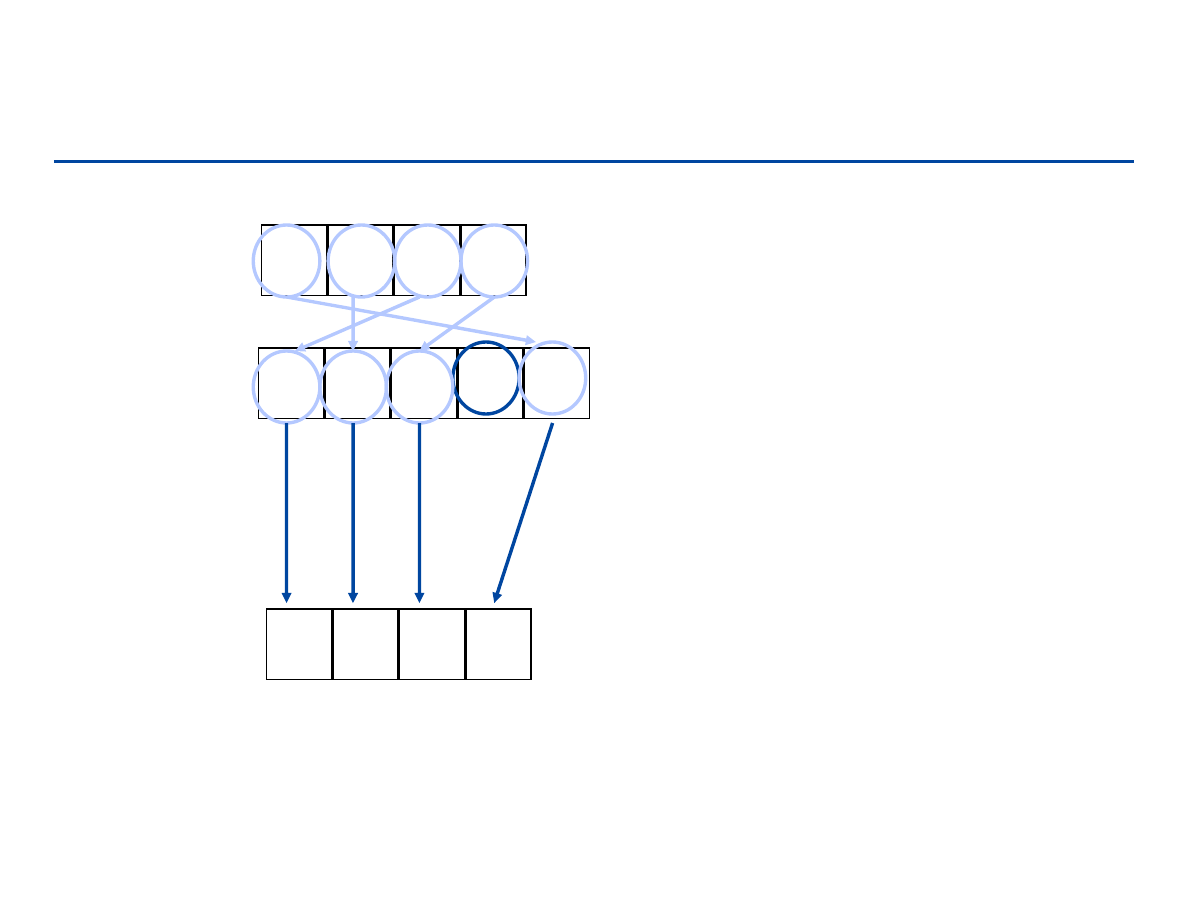
125

Zliczanie (Counting sort)

5

1

2

3

A =

3

2

4

Rank =

Jeśli nie ma powtórzeń i n < k

,

Niektóre komórki tablicy rank
pozostają niewykorzystane, ale
algorytm działa.

B =

5

2

1

1

3

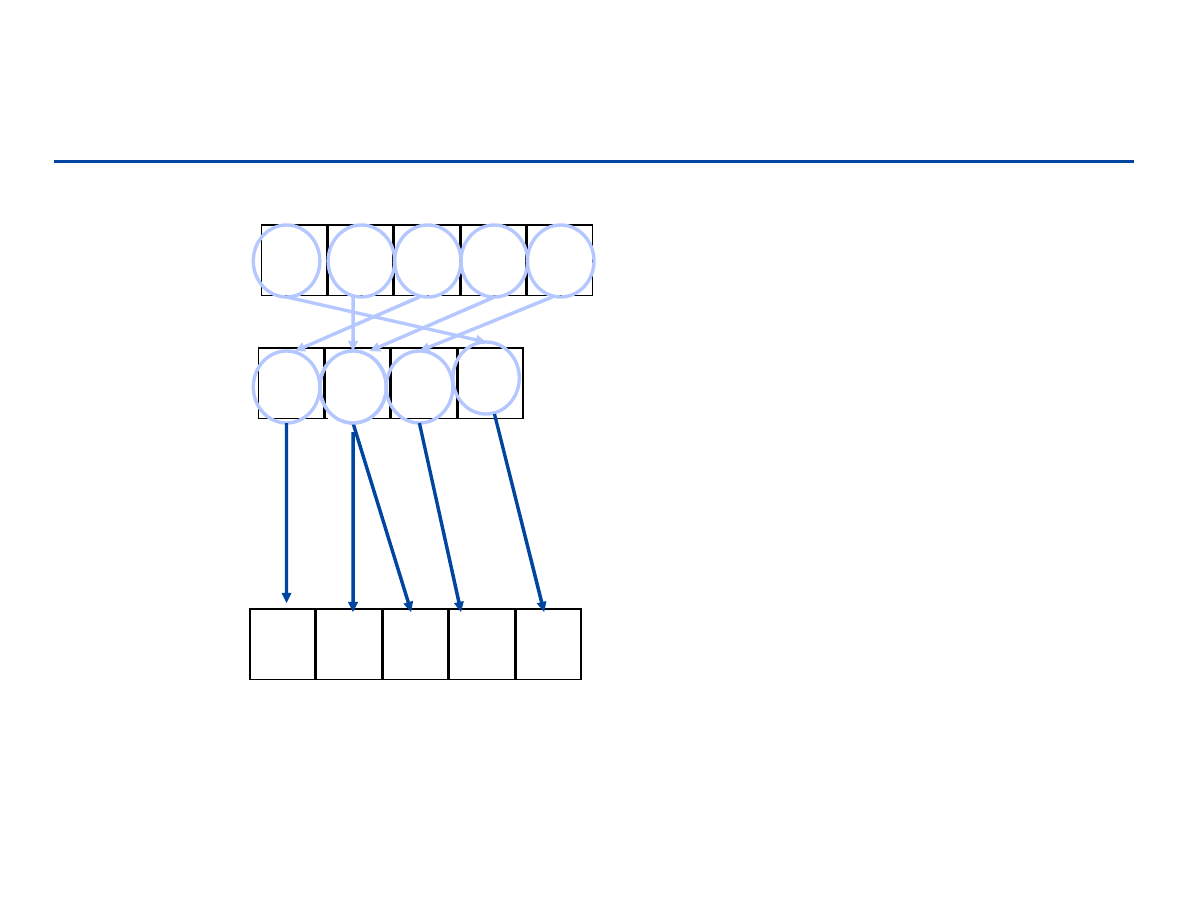
126

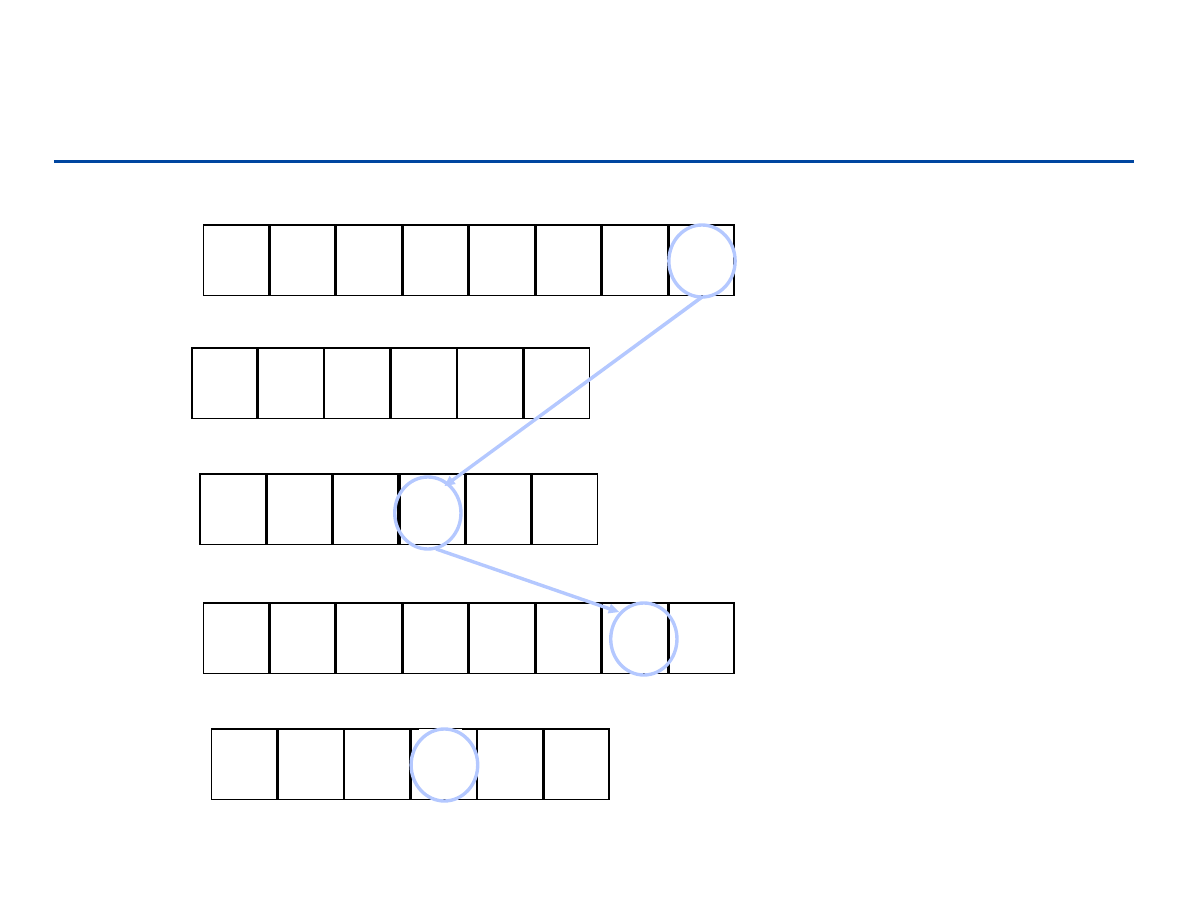
Zliczanie (Counting sort)

4

1

2

2

A =

1

4

3

5

Rank =

Jeśli n > k i mamy powtórzenia,

umieszczamy na wyjściu
powtarzające się elementy w
takiej kolejności, w jakiej
występowały w oryginalnym
ciągu (stabilność)

B =

3

3

4

2

1

2

2

127

Zliczanie (Counting sort)

Counting-Sort(A, B, k)
1.

for i 0 to k

2.

do C[i] 0

3.

for j

1 to length[A]

4.

do C[A[j]] C[A[j]] +1

5.

/* C zawiera ilości elementów równych i

6.

for i 1 to k

7.

do C[i] C[i] + C[i –1]

8.

/* C zawiera ilości elementów ≤ i

9.

for j length[A] downto 1

10.

do B[C[A[j]]] A[j]

11.

C[A[j]] C[A[j]] – 1

A[1..n] – tablica wejściowa
B [1..n] – tablica wyjściowa
C [0..k] – pomocnicza tablica (do zliczania)

128

Sortowanie przez zliczanie – przykład (1)

n = 8
k = 6

B[C[A[j]]] A[j]
C[A[j]] C[A[j]] – 1
po p. 11

C[A[j]] C[A[j]] +1
po p.4

C =

0 1 2 3 4 5

2

2

0

3

0

1

2

3

5

0

2

3

0

3

A =

1 2 3 4 5 6 7 8

2

4

2

7

7

8

C =

0 1 2 3 4 5

C[i] C[i] + C[i –1]
po p. 7

2

4

2

7

8

C =

0 1 2 3 4 5

7

1 2 3 4 5 6 7 8

B =

3

6

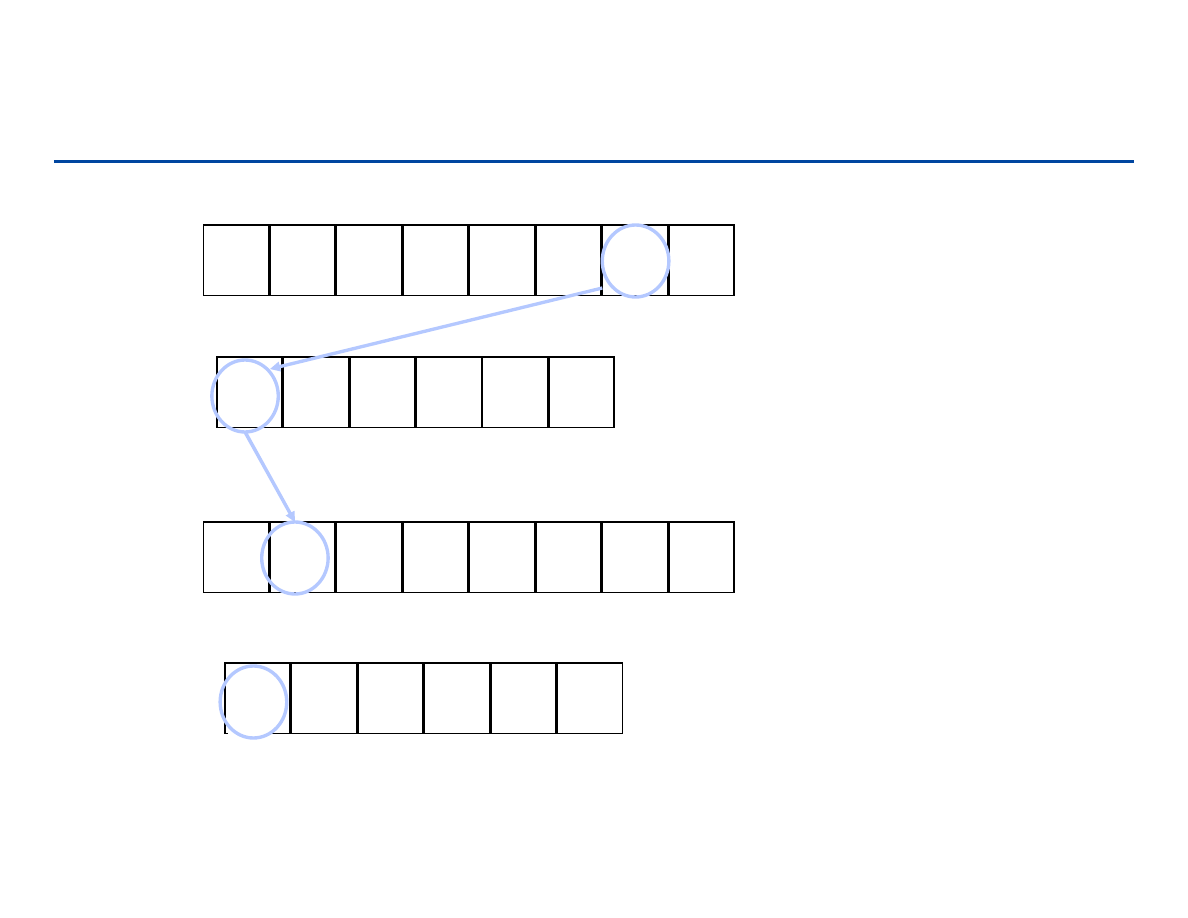
129

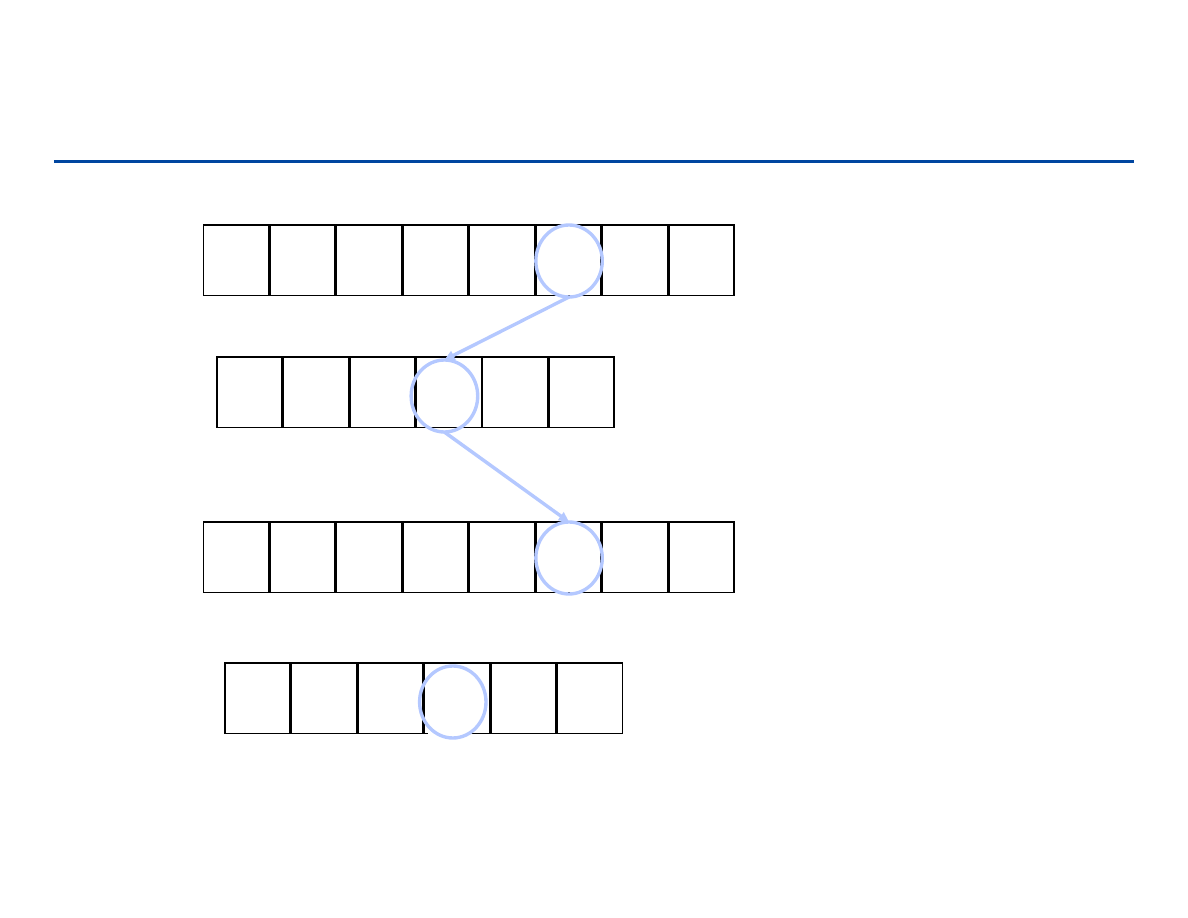
Sortowanie przez zliczanie – przykład (2)

0

3

B =

2

4

2

6

7

8

C =

0 1 2 3 4 5

1 2 3 4 5 6 7 8

2

3

5

0

2

3

0

3

A =

1 2 3 4 5 6 7 8

2

4

2

6

7

8

C =

0 1 2 3 4 5

1

130

Sortowanie przez zliczanie – przykład (3)

0

3

B =

1

4

2

6

7

8

C =

0 1 2 3 4 5

1 2 3 4 5 6 7 8

2

3

5

0

2

3

0

3

A =

1 2 3 4 5 6 7 8

2

4

2

6

7

8

C =

0 1 2 3 4 5

3

5

131

Counting sort – czas działania

Pętla for w p.1-2 zajmuje czas Θ(k)

Pętla for w p.3-4 zajmuje czas Θ(n)

Pętla for w p.6-7 zajmuje czas Θ(k)

Pętla for w p.9-11 zajmuje czas Θ(n)

Stąd dostajemy łączny czas Θ(n+k)

Ponieważ k = O(n), T(n) = Θ(n)

algorytm jest optymalny!!

Konieczne jest założenie k = O(n). Jeśli k >> n to potrzeba to

potrzeba dużej ilości pamięci.

Nie jest to sortowanie „w miejscu”.

132

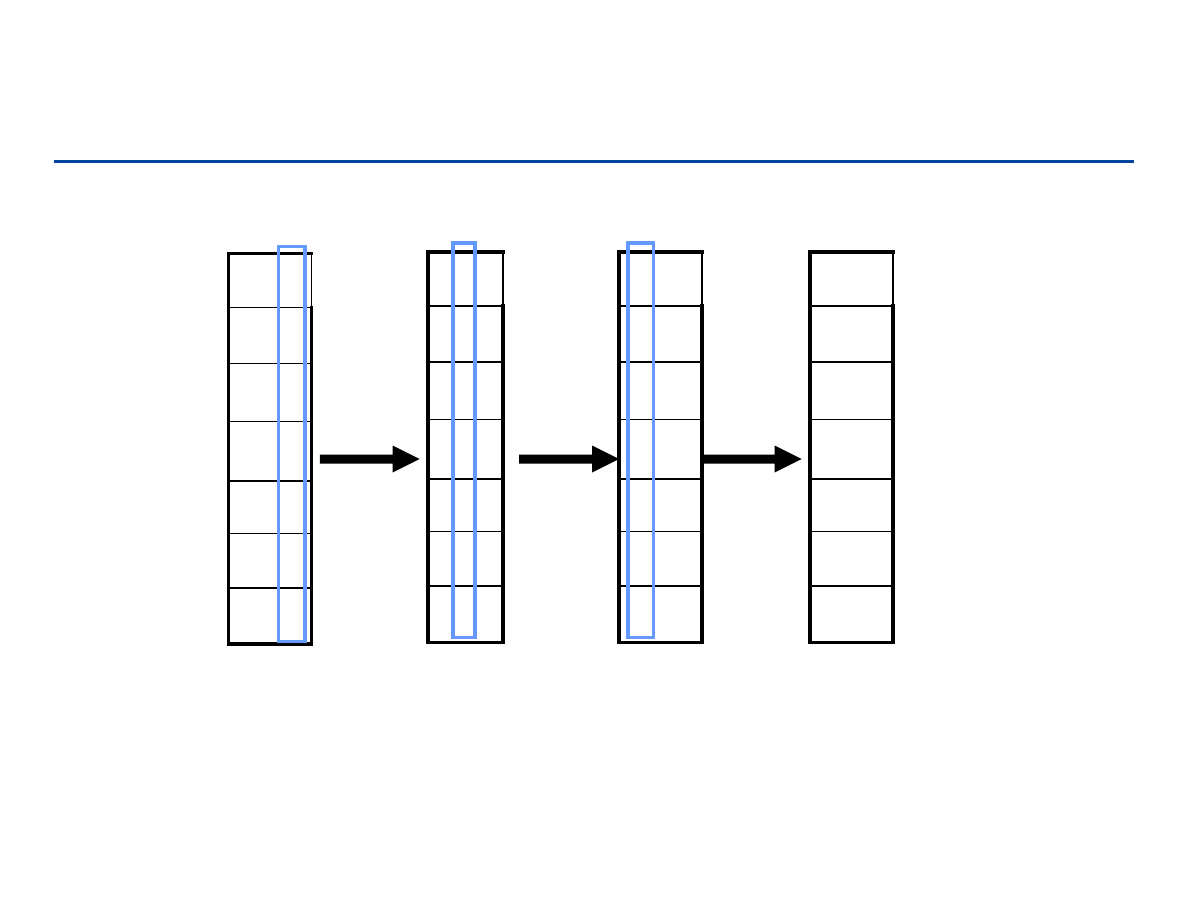
Radix sort – sortowanie pozycyjne

wejście: n liczb całkowitych, d-cyfrowych, łańcuchów o d-pozycjach

pomysł: zajmować się tylko jedną z cyfr (sortować względem kolejnych

pozycji – cyfr/znaków). Zaczynamy od najmniej znaczącej

cyfry/znaku, potem kolejne pozycje (cyfry/znaki), aż do najbardziej

znaczącej. Musimy stosować metodą stabilną. Ponieważ zbiór

możliwych wartości jest mały (cyfry – 0-9, znaki ‘a’-’z’) możemy

zastosować metodę zliczania, o czasie O(n)

Po zakończeniu ciąg będzie posortowany!!

133

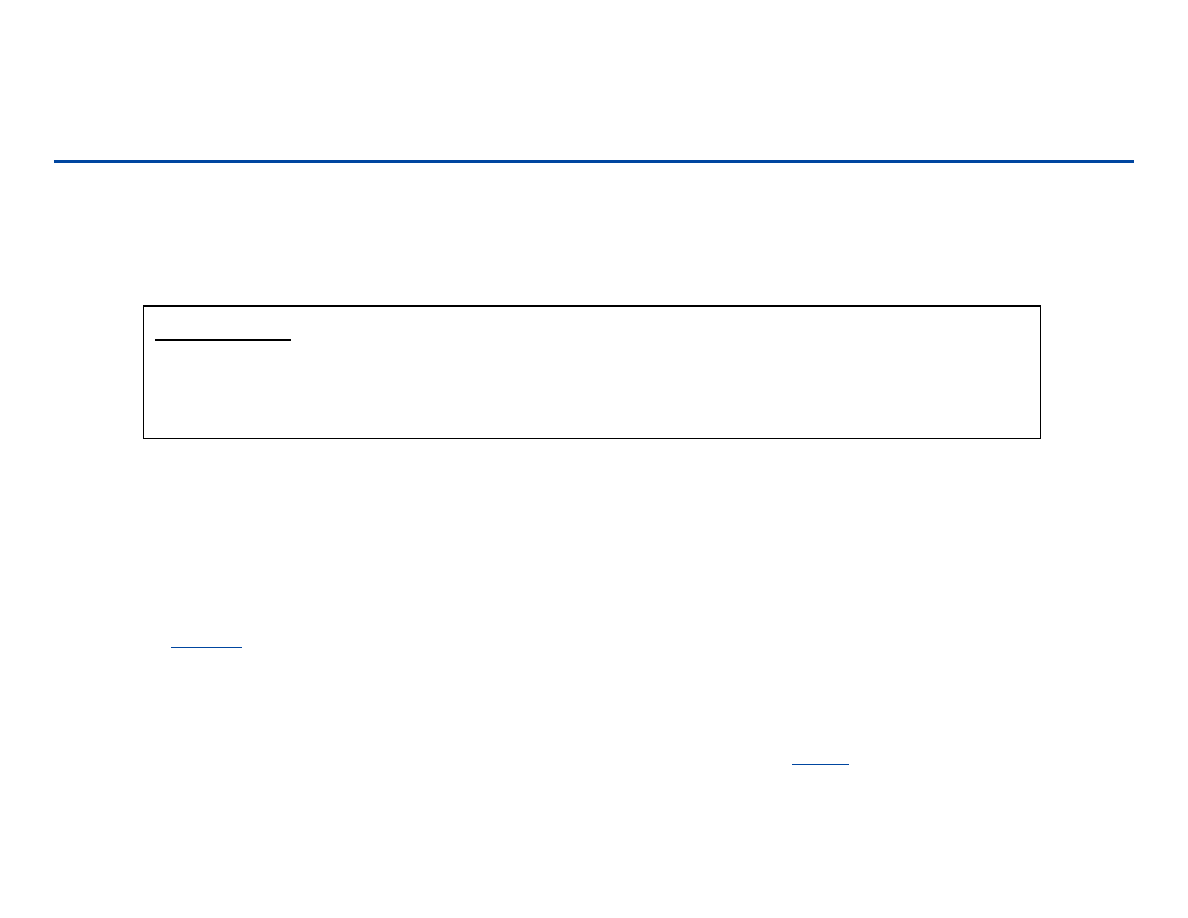
Radix sort – przykład

6 5 7

4 5 7

3 5 5

8 3 9

4 3 6

3 2 9

7 2 0

3 5 5

7 2 0

4 3 6

8 3 9

6 5 7

4 5 7

3 2 9

8 3 9

3 2 9

6 5 7

4 5 7

4 3 6

3 5 5

7 2 0

8 3 9

7 2 0

6 5 7

4 5 7

4 3 6

3 5 5

3 2 9

134

Radix-Sort – pseudokod

Radix-Sort(A, d)

1.

for i 1 to d

2.

do zastosuj stabilną metodę sortowania do cyfry d dla tablicy A

uwagi:

•

złożoność: T(n) = Θ(d(n+k)) Θ(n) dla stałego d i k = O(1)

•

wartości cyfr/znaków są z zakresu [0..k –1] dla k = O(1)

•

Metoda stosowana dla poszczególnych pozycji musi być stabilna!

135

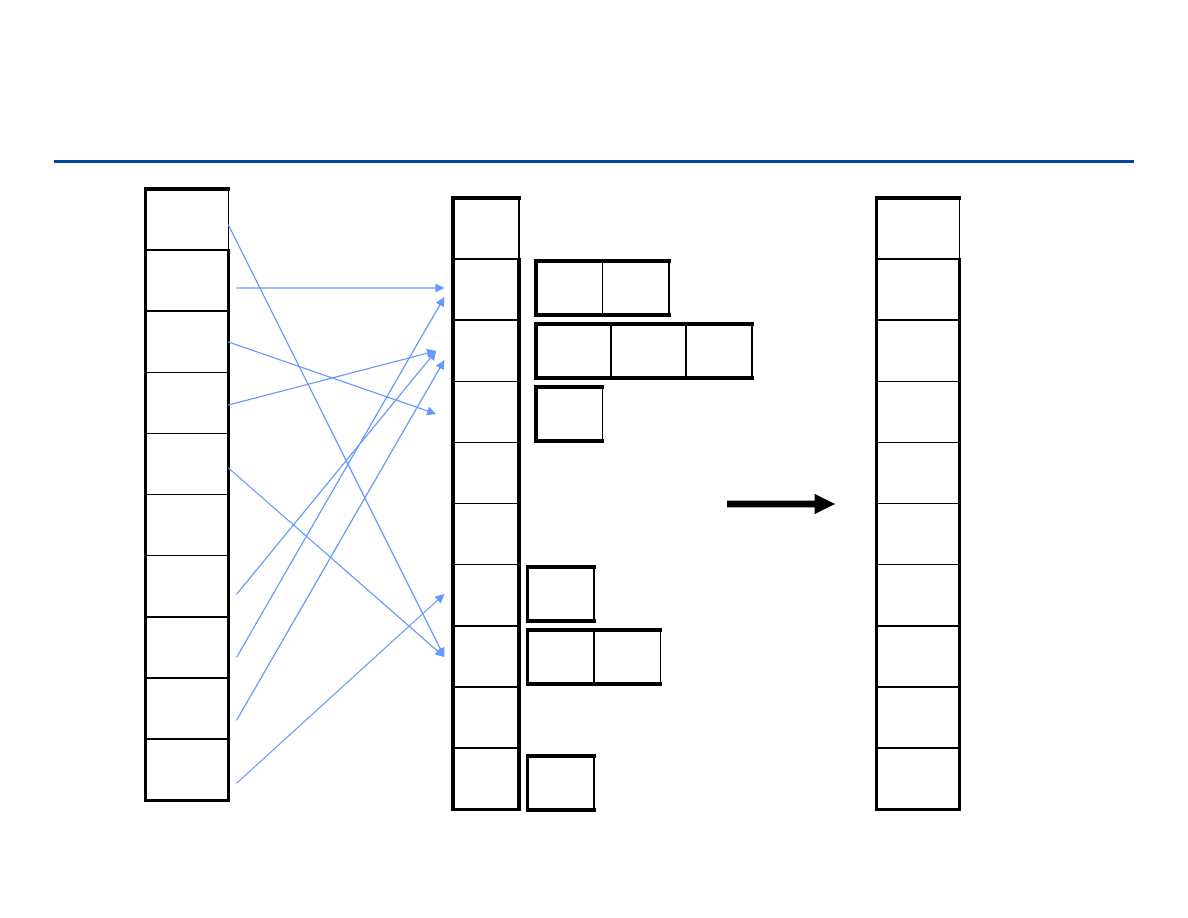
Sortowanie kubełkowe – Bucket sort

wejście: n liczb rzeczywistych z przedziału [0..1) ważne jest, aby były

równomiernie rozłożone (każda wartość równie prawdopodobna)

pomysł: dzielimy przedział [0..1) na n podprzedziałów („kubełków”):0, 1/n,

2/n. … (n–1)/n. Elementy do odpowiednich kubełków, a

i

: 1/i ≤ a

i

≤

1/(i+1).

Ponieważ rozkład jest równomierny to w żadnym z przedziałów nie

powinno znaleźć się zbyt wiele wartości. Jeśli wkładamy je do kubełków

zachowując porządek (np. przez wstawianie – Insertion-Sort),

dostaniemy posortowany ciąg.

136

Bucket sort – przykład

. 21

.12

.23

.68

.94

.72

.26

.39

.17

.78

7

6

8

9

5

4

3

2

1

0

.17

.12

.26

.23

.21

.39

.68

.78

.72

.94

.68

.72

.78

.94

.39

.26

.23

.21

.17

.12

137

Bucket-Sort

Bucket-Sort(A)
1.

n length(A)

2.

for i 0 to n

3.

do wstaw A[i] do listy B[floor(nA[i])]

4.

for i 0 to n –1

5.

do Insertion-Sort(B[i])

6.

Połącz listy B[0], B[1], … B[n –1]

A[i] tablica wejściowa
B[0], B[1], … B[n –1] lista „kubełków”

138

Bucket-Sort – złożoność czasowa

Wszystkie instrukcje z wyjątkiem 5 (Insertion-Sort) wymagają czasu O(n),

w przypadku pesymistycznym.

W przypadku pesymistycznym, O(n) liczb trafi do jednego „kubełka” czyli

ich sortowanie zajmie czas O(n

2

).

Jednak w średnim przypadku stała ilość elementów wpada do jednego

przedziału – stąd czas średni wyniesie O(n).

139

Sortowanie

Quicksort i Heapsort

140

Sortowanie - zadanie

Definicja (dla liczb):

wejście: ciąg n liczb A = (a

1

, a

2

, …, a

n

)

wyjście: permutacja (a

1

,…, a’

n

) taka, że a’

1

≤

… ≤ a’

n

141

Zestawienie czasów działania

Przez wybór: O(N

2

) zawsze

Bąbelkowe: O(N

2

) najgorszy przypadek; O(N) najlepszy przyp.

Wstawianie: O(N

2

) średnio; O(N) najlepszy przypadek

Shellsort:

O(N

4/3

)

Heapsort:

O(NlogN) zawsze

Mergesort:

O(NlogN) zawsze

Quicksort:

O(NlogN) średnio; O(N

2

) najgorszy przypadek

Zliczanie:

O(N) zawsze

Radix sort:

O(N) zawsze

zewnętrzne: O(b logb)) dla pliku o b „stronach”.

142

Dzisiaj:

Dwa algorytmy sortowania:

Quicksort

– Bardzo popularny algorytm, bardzo szybki w średnim przypadku

Heapsort

– Wykorzystuje strukturę kopca (heap)

143

Sortowanie szybkie (Quick Sort) - pomysł

Jest to najszybszy w praktyce algorytm sortowania, pozwala na

efektywne implementacje.

– średnio: O(NlogN)

– najgorzej O(N

2

), przypadek bardzo mało prawdopodobny.

Procedura:

– Wybieramy element osiowy (pivot ).

– Dzielimy ciąg na dwa podciągi: elementów mniejszych lub równych

od osiowego oraz elementów większych od osiowego. Powtarzamy

takie postępowanie, aż osiągniemy ciąg o długości 1.

– Algorytm typu – „dziel i zwyciężaj”.

– Jest to metoda sortowania w miejscu (podobnie jak Insert-sort,

przeciwnie do np. Merge-sort), czyli nie wymaga dodatkowej

pamięci

144

Quicksort – algorytm

QUICKSORT(A, p, r)

1

if p < r

2

then q ← PARTITION(A, p, r)

3 QUICKSORT(A, p, q - 1)

4 QUICKSORT(A, q + 1, r)

Problemy:

1.

Wybór elementu osiowego;

2.

Podział (partition).

145

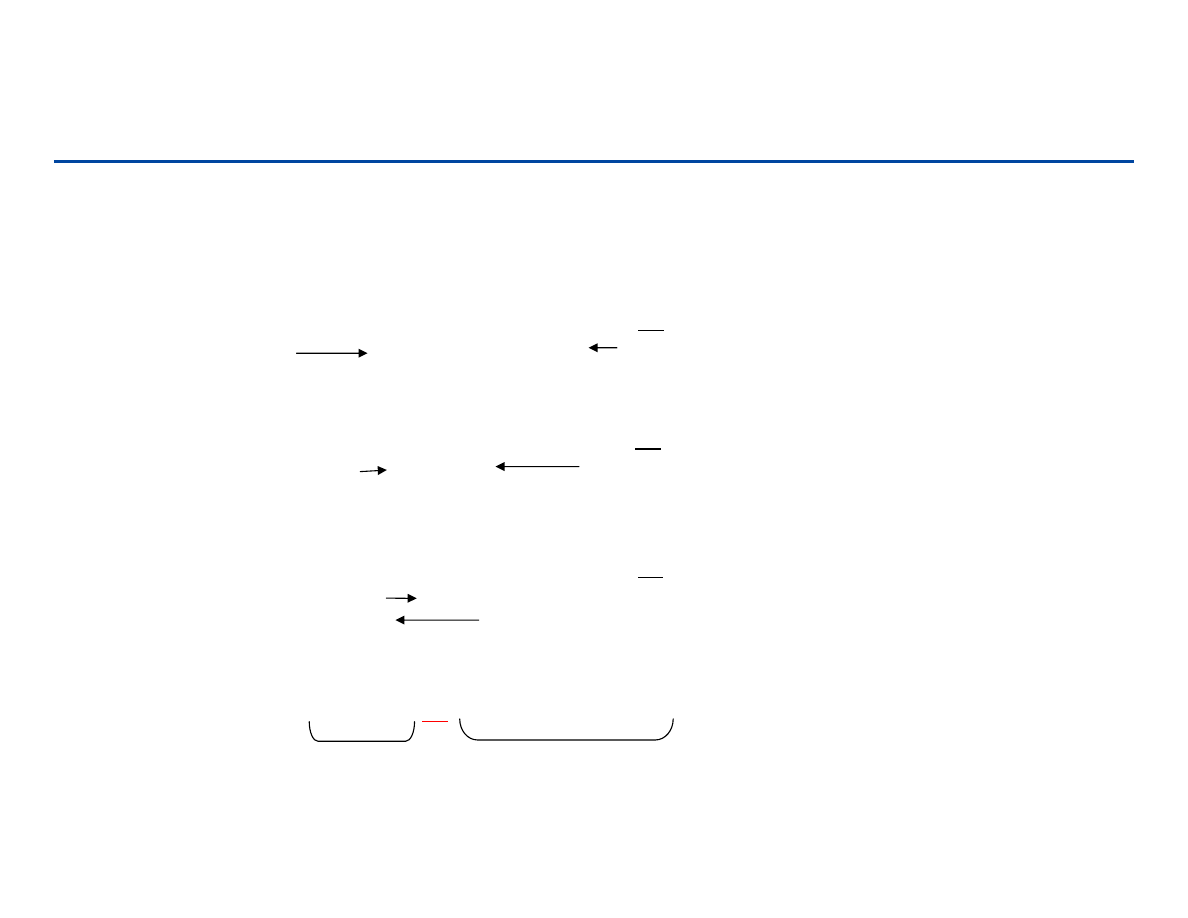
Quicksort – podział

Funkcja partition dzieli ciąg na dwa podciągi: elementów

mniejszych (bądź równych) od osiowego i większych od niego

{a[j] | a[j] <= a[i]

dla j ∈[left, i-1]}

{a[k] | a[k] > a[i]
dla k ∈[i+1,right]}

a[i]

wynik

quicksort(a, left, i-1)

wynik

quicksort(a, i+1, right)

Po podziale:

El. osiowy

146

Quicksort – przykład podziału

ciąg: EASYQUESTION (12 znaków).

El. osiowy: N

E A S Y Q U E S T I O N

Przeglądaj aż: a[i] > a[right]

Przeglądaj aż:

a[j] <= a[right]

i

j

Swap(a[i], a[j])

E A

I

Y Q U E S T

S

O N

i

j

Swap(a[i], a[j])

E A

I

E

Q U

Y

S T

S

O N

i

j

Swap(a[i], a[right])

(indeksy i oraz j „minęły” się)

E A

I

E

N

U

Y

S T

S

O

Q

Lewy podciąg

Prawy podciąg

147

Quicksort – wybór elementu osiowego

opcja 1: zawsze wybierać skrajny element (pierwszy lub ostatni).

– Zalety: szybkość;

– Wady: jeśli trafimy na najmniejszy (największy) element podział nie

redukuje istotnie problemu.

opcja 2: wybieramy losowo.

– Zalety: średnio powinno działać dobrze (podział na podciągi o

zbliżonej długości);

– Wady: czasochłonne i nie gwarantuje sukcesu.

opcja 3: wybieramy medianę z pierwszych/ostatnich/środkowych 3/5/7

elementów.

– gwarantuje, że nie będzie zdegenerowanych podciągów (pustych).

– kompromis pomiędzy opcją 1 i 2

148

Podział – pseudokod (opcja 1)

Partition(A, Left, Right)

1.

Pivot

A[Right]

2.

i

Left – 1

3.

for

j Left to Right–1

4.

do if

(A[j] ≤ Pivot)

5.

then

i

i + 1

6.

Exchange(A[i], A[j])

7.

Exchange (A[i+1], A[Right])

8.

return

i +1

149

Randomizowany Quicksort (opcja 2)

Zakładamy że nie ma powtórzeń
Jako element osiowy wybieramy losowy element ciągu (opcja 2)
Powtarzamy procedurę, wszystkie podziały są równie prawdopodobne

(1:n-1, 2:n-2, ..., n-1:1), z prawdopodobieństwem 1/n

Randomizacja jest drogą do unikania najgorszego przypadku

150

Randomizowany Quicksort

Randomized-Partition(A,p,r)

01 i←Random(p,r)
02 exchange A[r] ↔A[i]
03

return Partition(A,p,r)

Randomized-Quicksort(A,p,r)

01

if p<r then

02

q←Randomized-Partition(A,p,r)

03

Randomized-Quicksort(A,p,q)

04

Randomized-Quicksort(A,q+1,r)

151

Quicksort – czas działania

Najgorszy przypadek: O(N

2

)

– Podciągi zawsze mają długości 0 i N-1 (el. Osiowy jest zawsze

najmniejszy/największy). Np. dla posortowanego ciągu i pierwszej

opcji wyboru el. osiowego.

Najlepszy przypadek: O(NlogN)

– Podział jest zawsze najlepszy (N/2). El. osiowy zawsze jest

medianą.

Średnio: O(NlogN)

152

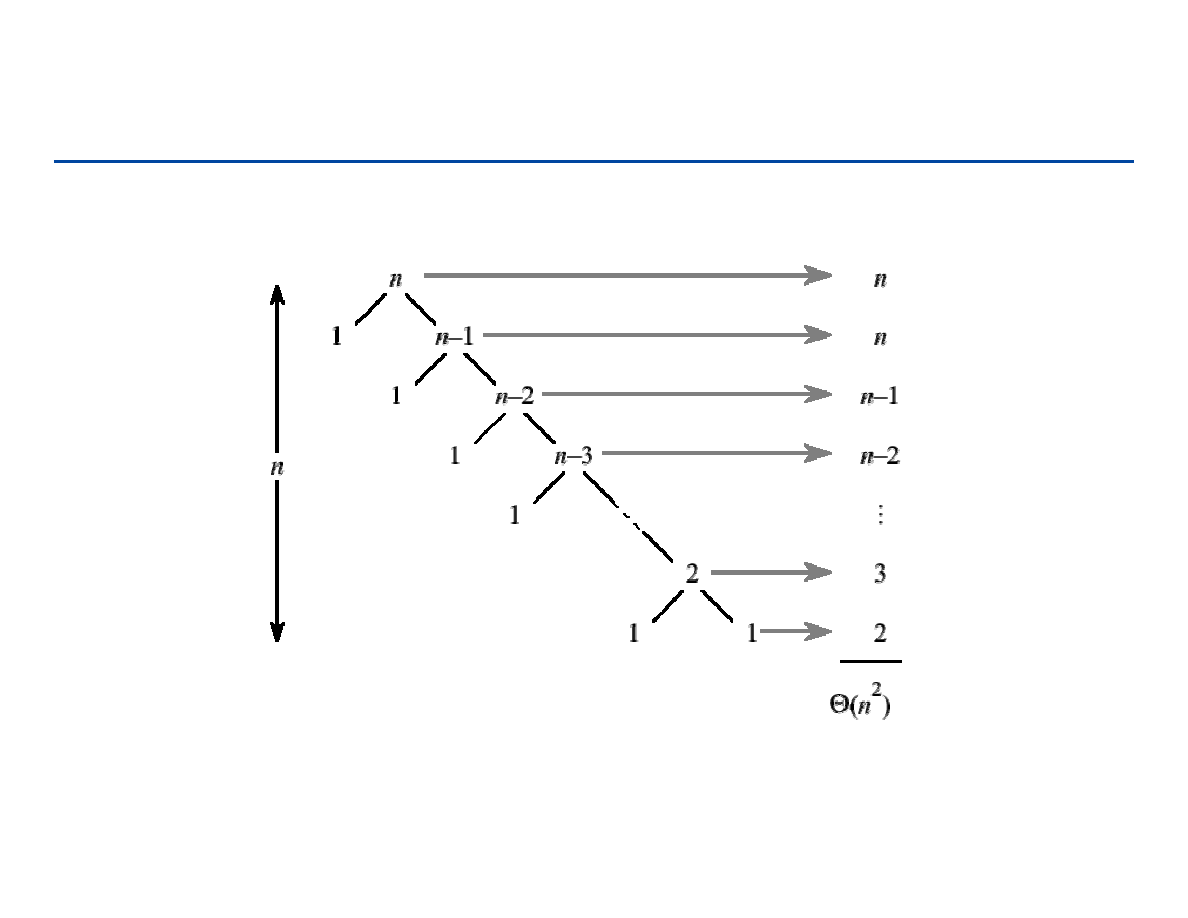
Quicksort – najlepszy przypadek

Podciągi otrzymane w wyniku podziału są równe

( )

2 ( / 2)

( )

T n

T n

n

=

+ Θ

153

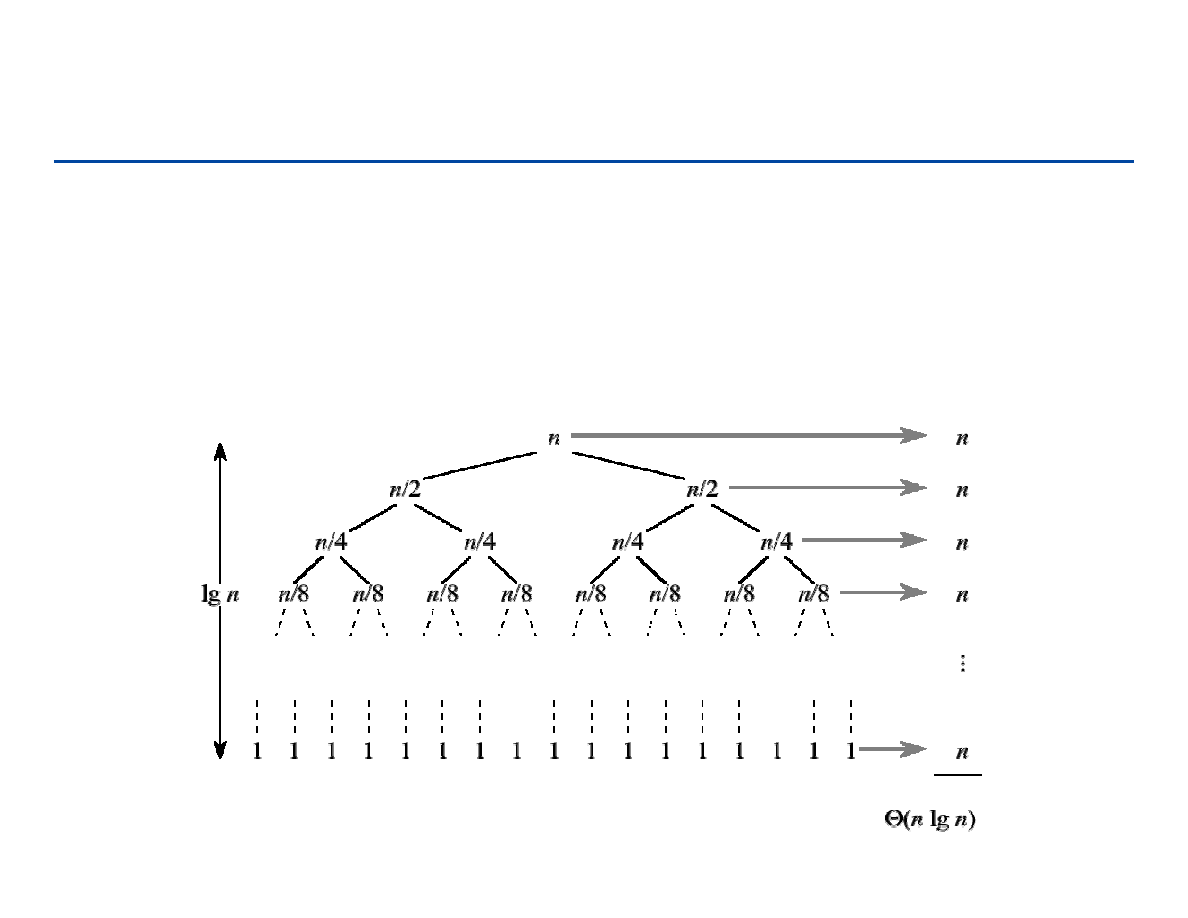
Quicksort – najgorszy przypadek

154

Quicksort- czas działania

T(N) = T(i) + T(N-i-1) + N for N > 1

T(0) = T(1) = 1

– T(i) i T(N-i-1) dla podziału i/N-i-1.

– N dla podziału 1/N-1(liniowe – przeglądamy wszystkie elementy).

155

Quicksort – czas działania

najgorzej: T(N) = T(0) + T(N-1) + N = T(N-1) + N = O(N

2

)

najlepiej: T(N) = 2T(N/2) + N = O(NlogN)

„średnio”:

T(N) = (1/N) ∑

∑

∑

∑

i=0

N-1

T(i) + (1/N) ∑

∑

∑

∑

i=0

N-1

T(N-i-1) + N

= (2/N) ∑

∑

∑

∑

j=0

N-1

T(j) + N = O(NlogN)

156

Quicksort - uwagi

Małe ciągi

– Quicksort zachowuje się źle dla krótkich ciągów.

– Poprawa – jeśli podciąg jest mały zastosować sortowanie przez

wstawianie (zwykle dla ciągów o długości 5 ~ 20)

Porównanie z mergesort:

– Oba zbudowane na zasadzie „dziel i zwyciężaj”.

– Mergesort wykonuje sortowanie w fazie łączenia.

– Quicksort wykonuje prace w fazie podziału.

157

Heap Sort – pojęcie kopca

Struktura kopca binarnego

– Drzewo binarne (bliskie zrównoważenia)

• Wszystkie poziomy, z wyjątkiem co najwyżej ostatniego, kompletnie

zapełnione

– Wartość klucza w węźle jest większa lub równa od wartości kluczy

wszystkich dzieci; własność taka jest zachowana dla lewego i prawego
poddrzewa (zawsze)

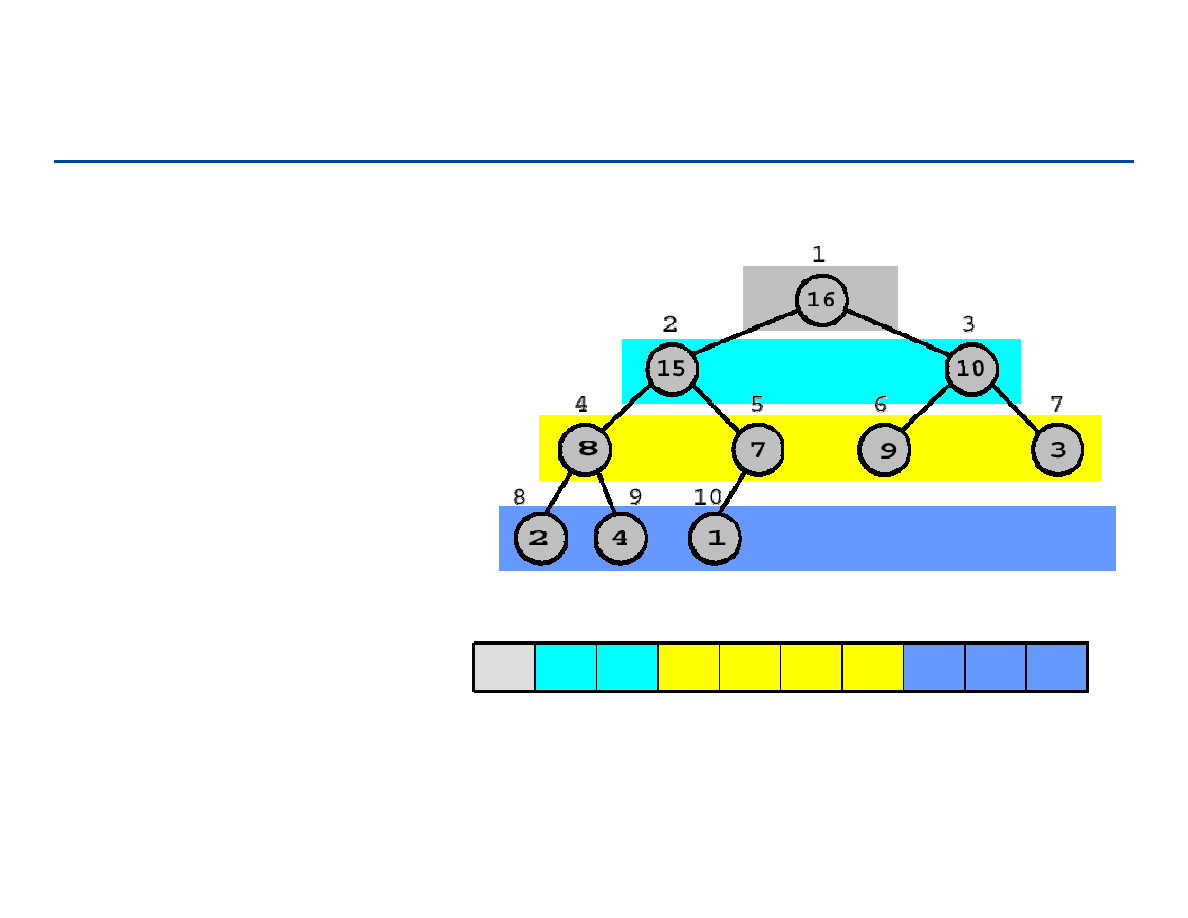
158

Heap Sort – reprezentacja tablicowa kopca

1

4

2

3

9

7

8

10

15

16

10

9

8

7

6

5

4

3

2

1

Parent (

i

)

return 

i

/2

Left (

i

)

return 2

i

Right (

i

)

return 2

i

+1

Własność kopca:

A

[Parent(

i

)] ≥

A

[

i

]

poziomy: 3

2

1

0

159

Heap Sort – reprezentacja kopca w tablicy

Zauważmy połączenia w drzewie – dzieci węzła i występują na pozycjach

2i oraz 2i+1

Czemu to jest wygodne?

– Dla reprezentacji binarnej, dzieleniu/mnożeniu przez 2 odpowiada

przesuwanie (szybka operacja)

– Dodawanie jedynki oznacza zmianę najmłodszego bitu (po przesunięciu)

160

Kopcowanie (Heapify)

Niech i będzie indeksem w tablicy A

Niech drzewa binarne Left(i) i Right(i) będą kopcami

Ale, A[i] może być mniejsze od swoich dzieci – co powoduje złamanie

własności kopca

Metoda Kopcowania (Heapify) przywraca własności kopca dla A poprzez

przesuwanie A[i] w dół kopca aż do momentu, kiedy własność kopca jest

już spełniona

161

Kopcowanie (Heapify)

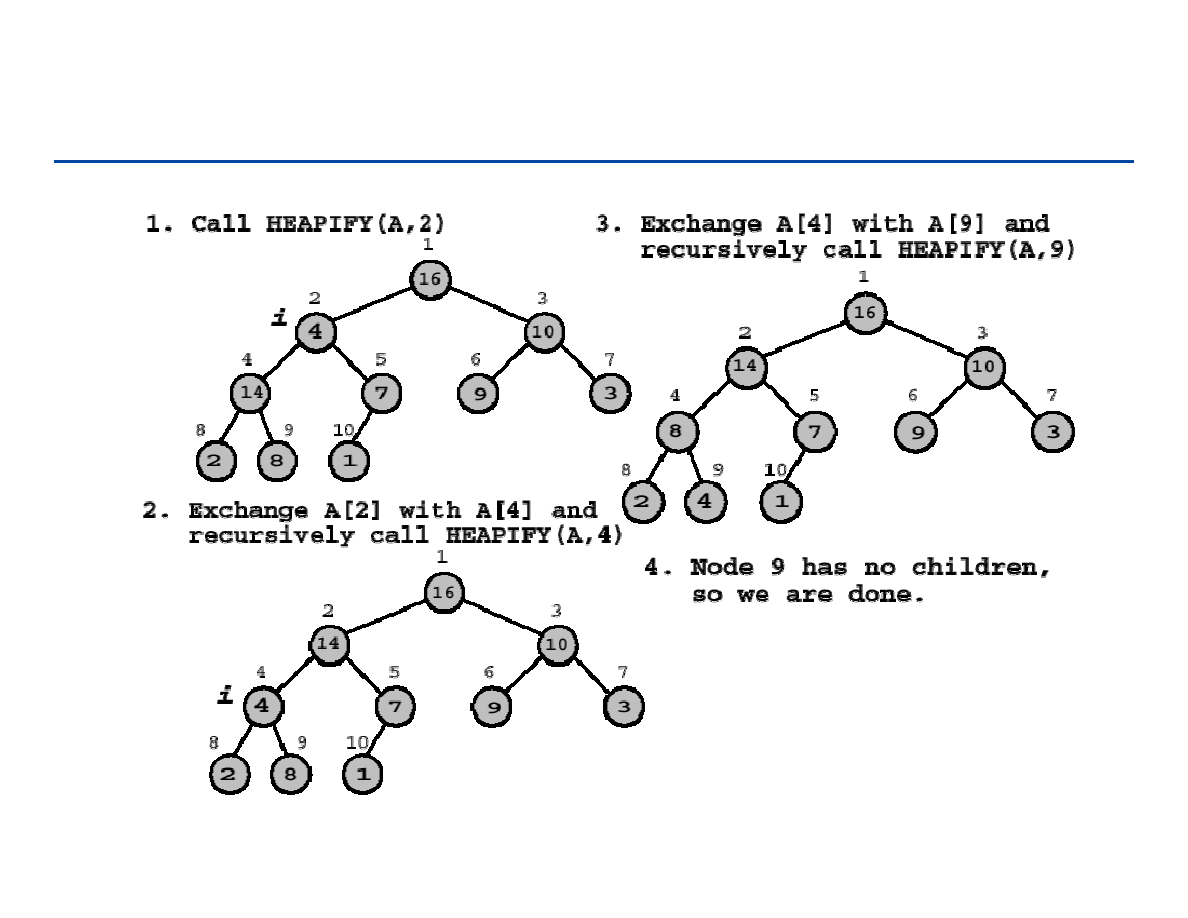
162

Kopcowanie (Heapify) – przykład

163

Kopcowanie – czas działania

Czas działania procedury Heapify dla poddrzewa o n węzłach i korzeniu

w i:

– Ustalenie relacji pomiędzy elementami: Θ(1)

– dodajemy czas działania Heapify dla poddrzewa o korzeniu w jednym z

potomków i, gdzie rozmiar tego poddrzewa 2n/3 jest najgorszym

przypadkiem.

– Inaczej mówiąc

• Czas działania dla drzewa o wysokości h: O(h)

( )

(2 / 3)

(1)

( )

(log )

T n

T

n

T n

O

n

≤

+ Θ

⇒

=

164

Budowa kopca

Konwertujemy tablicę A[1...n], gdzie n = length[A], na kopiec

Zauważmy, że elementy w A[(n/2 + 1)...n] są już zbiorem kopców -

jednoelementowych!

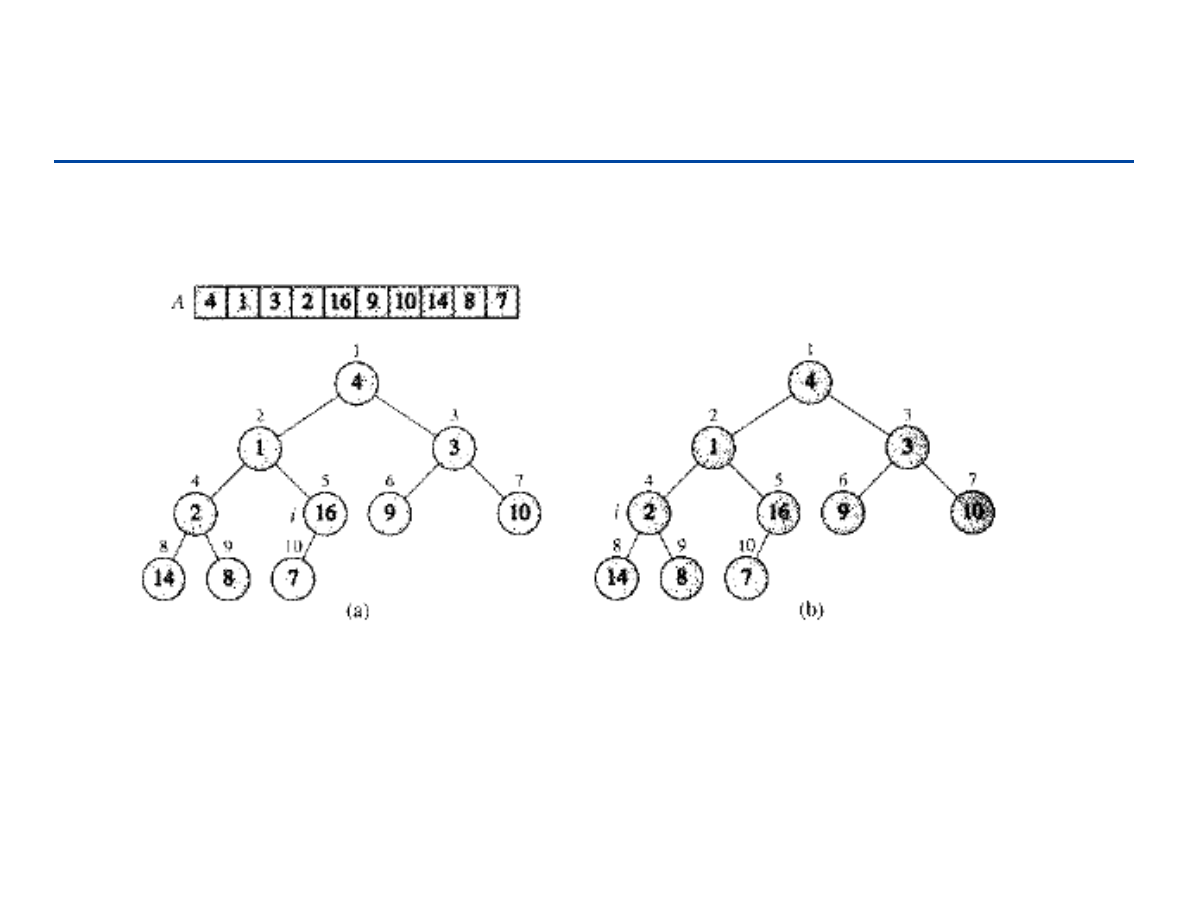
165

Budowanie kopca – 1

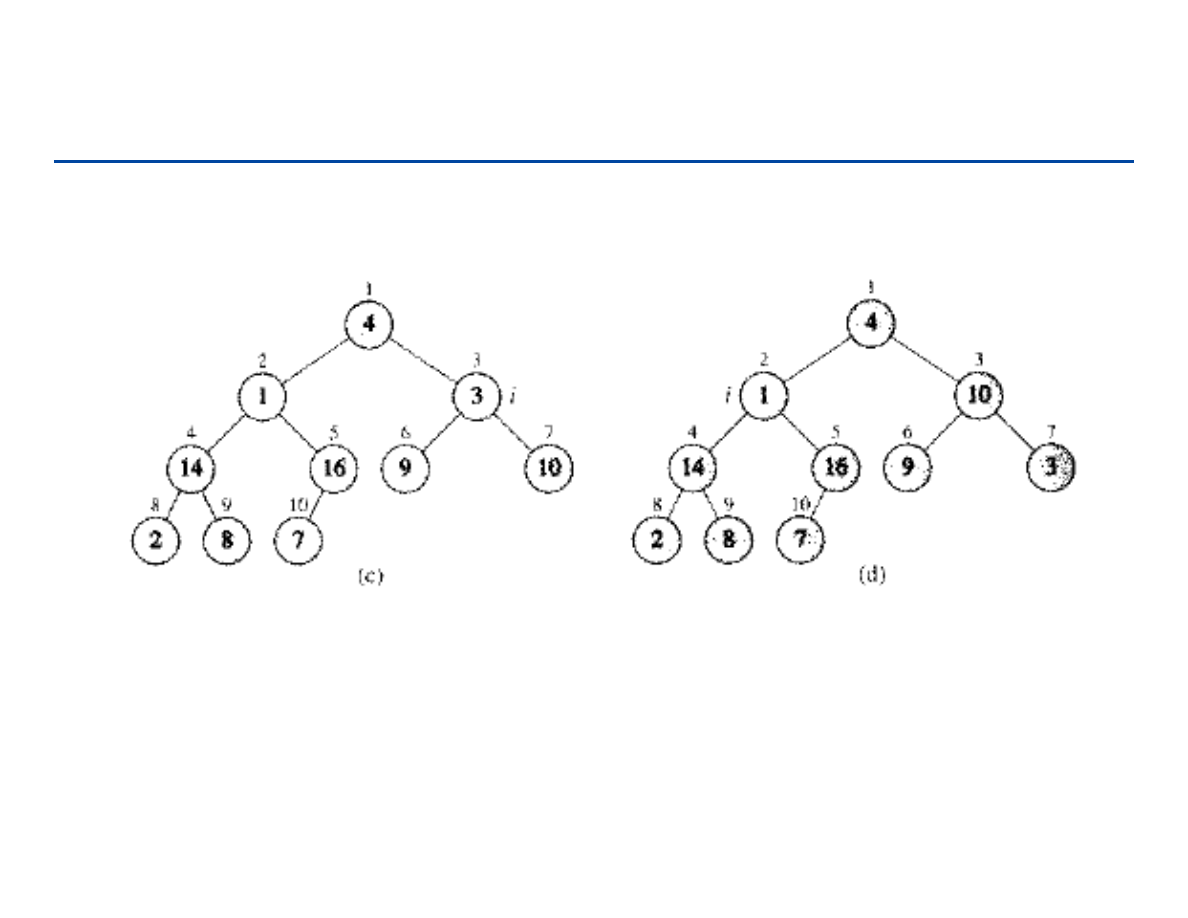
166

Budowanie kopca – 2

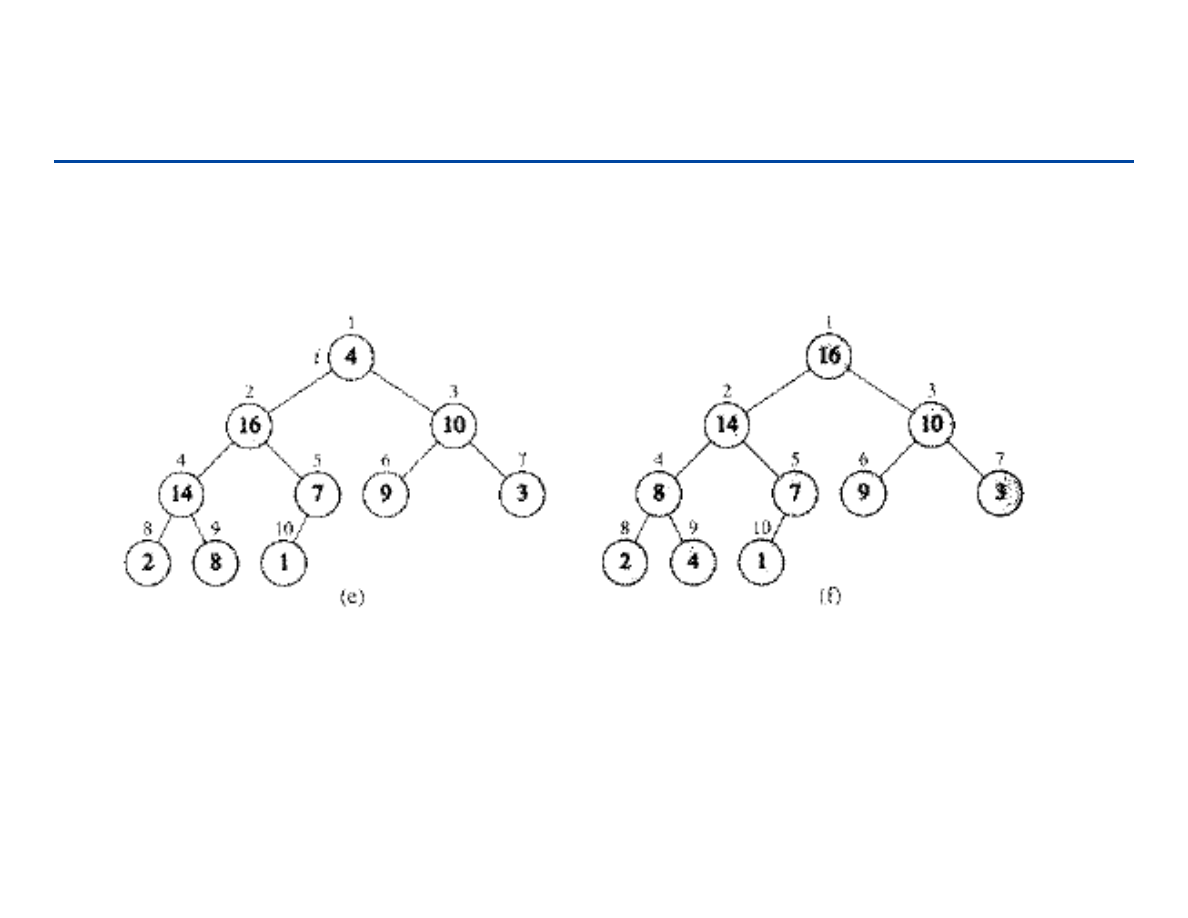
167

Budowanie kopca – 3

168

Budowa kopca – analiza

Poprawność: indukcja po i, (wszystkie drzewa o korzeniach m > i są

kopcami)

Czas działania: n wywołań kopcowania (Heapify) = n O(lg n) = O(n lg n)

Wystarczająco dobre ograniczenie – O(n lg n) dla zadania sortowanie

(Heapsort), ale czasem kopiec budujemy dla innych celów

169

Sortowanie za pomocą kopca – Heap Sort

Czas działania O(n lg n) + czas budowy kopca (O(n))

O( )

n

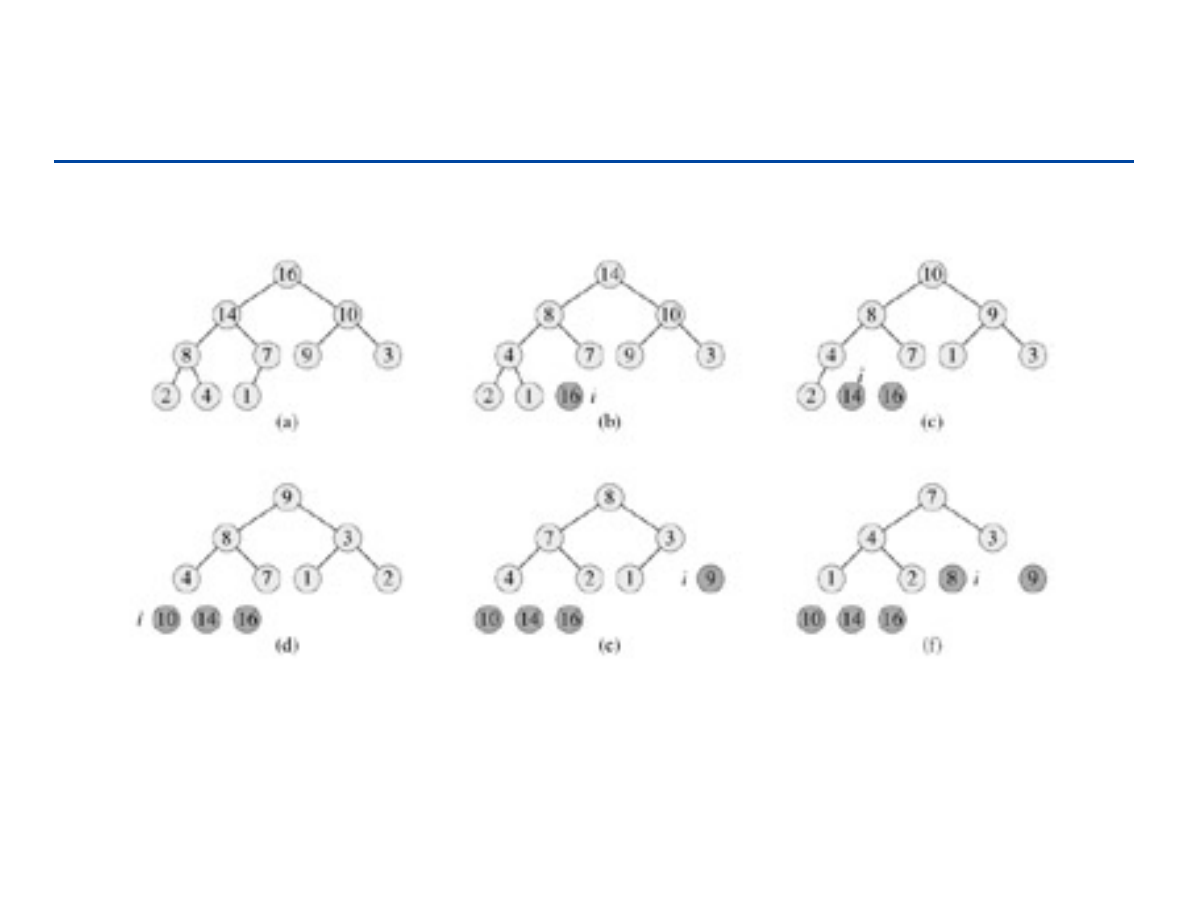
170

Heap Sort – 1

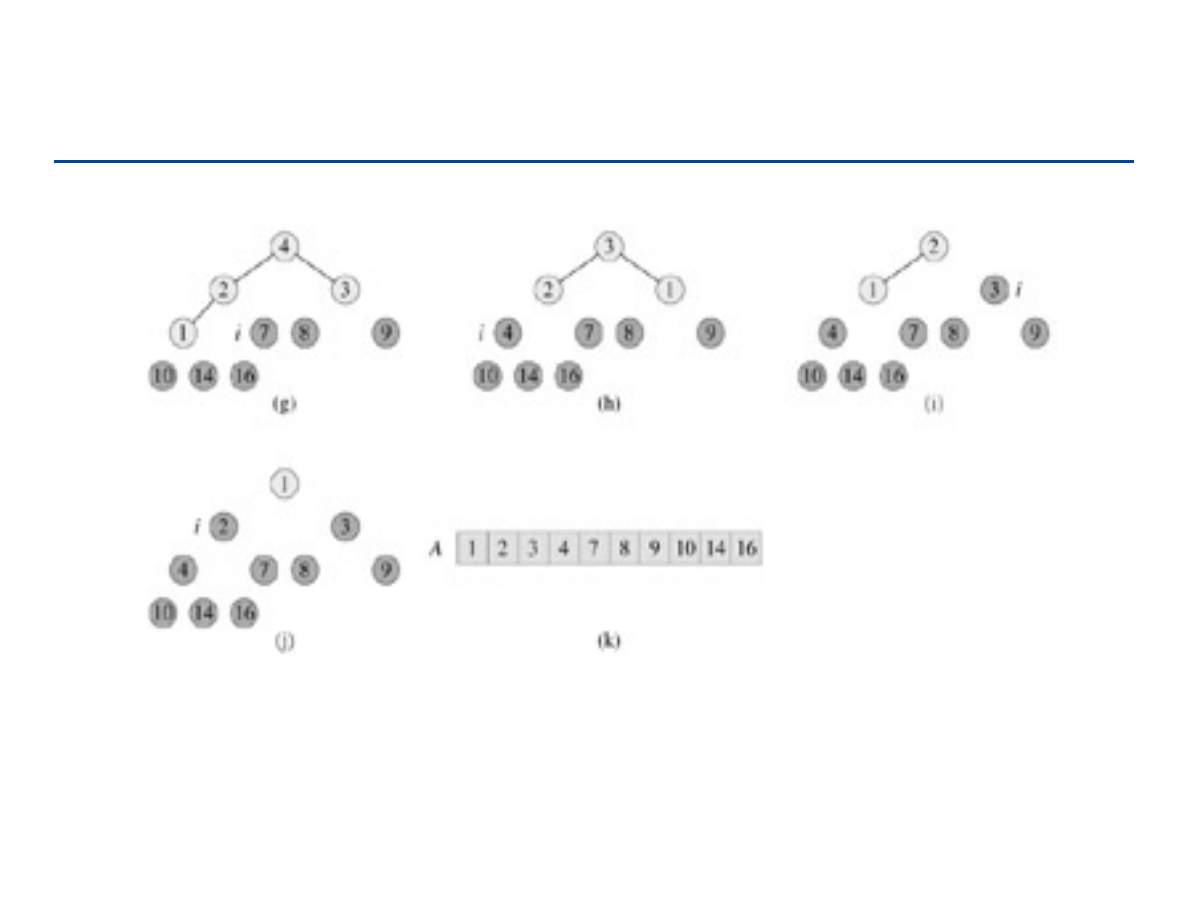
171

Heap Sort – 2

172

Heap Sort – podsumowanie

Heap sort wykorzystuje strukturę kopca przez co dostajemy

asymptotycznie optymalny czas sortowania

Czas działania O(n log n) – podobnie do merge sort, i lepiej niż wybór,

wstawianie czy bąbelkowe

Sortowanie w miejscu – podobnie do sortowania przez wybór, wstawianie

czy bąbelkowego

173

Dynamiczne struktury danych

174

Wprowadzenie

Popularne dynamiczne struktury danych (ADT)

stosy, kolejki, listy – opis abstrakcyjny

Listy liniowe

Implementacja tablicowa stosu i kolejki

Drzewa

Możliwe implementacje

Plan wykładu

175

Wprowadzenie

Do tej pory najczęściej zajmowaliśmy się jedną strukturą danych –

tablicą. Struktura taka ma charakter statyczny – jej rozmiar jest

niezmienny. Powoduje to konieczność poznania wymaganego rozmiaru

przed rozpoczęciem działań (ewentualnie straty miejsca – deklarujemy

„wystarczająco” dużą tablicę).

W wielu zadaniach wygodniejsza jest struktura o zmiennym rozmiarze

(w zależności od aktualnych potrzeb) – struktura dynamiczna.

Potrzebujemy struktury pozwalającej na przechowywanie elementów

niezależnie od ich fizycznego położenia.

logicznie

fizycznie

2

5

0

3

4

1

3

4

2

1

0

5

176

Wprowadzenie

Przykładowe operacje dla struktur danych:

–

Insert(S, k): wstawianie nowego elementu

–

Delete(S, k): usuwanie elementu

–

Min(S), Max(S): odnajdowanie najmniejszego/największego elementu

–

Successor(S,x), Predecessor(S,x): odnajdowanie

następnego/poprzedniego elementu

Zwykle przynajmniej jedna z tych operacji jest kosztowna czasowo

(zajmuje czas O(n)). Czy można lepiej?

177

Abstrakcyjne typy danych (Abstract Data Types –ADT )

Abstrakcyjnym typem danych nazywany formalną specyfikację sposobu

przechowywania obiektów oraz zbiór dobrze opisanych operacji na tych

obiektach.

Jaka jest różnica pomiędzy strukturą danych a ADT?

struktura danych (klasa) jest implementacją ADT dla specyficznego
komputera i systemu operacyjnego.

178

Popularne dynamiczne ADT

Listy łączone

Stosy, kolejki

Drzewa – z korzeniem (rooted trees), binarne, BST, czerwono-

czarne, AVL itd.

Kopce i kolejki priorytetowe (późniejsze wykłady)

Tablice z haszowaniem (późniejsze wykłady)

179

Listy

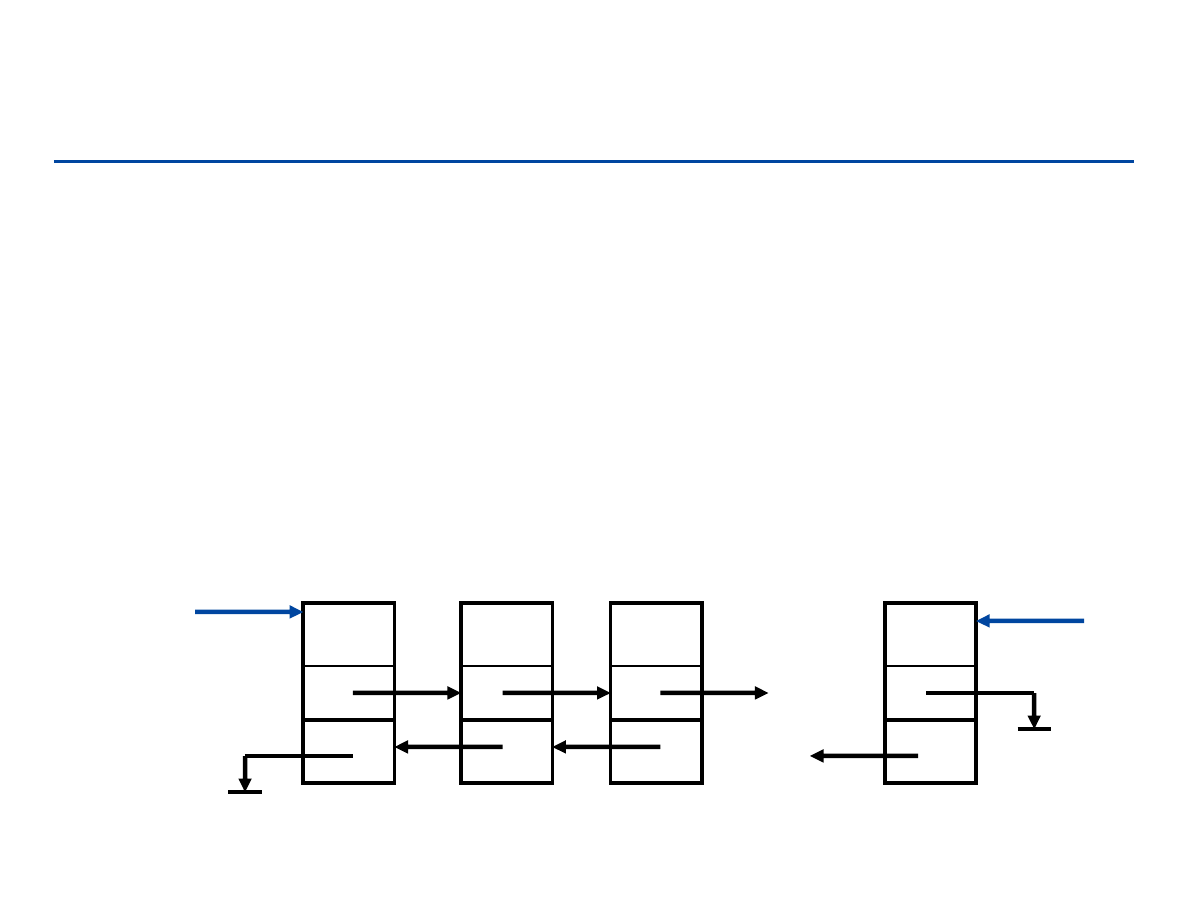
Lista L jest liniową sekwencją elementów.

Pierwszy element listy jest nazywany head, ostatni tail. Jeśli obydwa

są równe null, to lista jest pusta

Każdy element ma poprzednik i następnik (za wyjątkiem head i tail)

Operacje na liście:

– Successor(L,x), Predecessor(L,x)

– List-Insert(L,x)

– List-Delete(L,x)

– List-Search(L,k)

2

2

0

3

0

1

x

head

tail

180

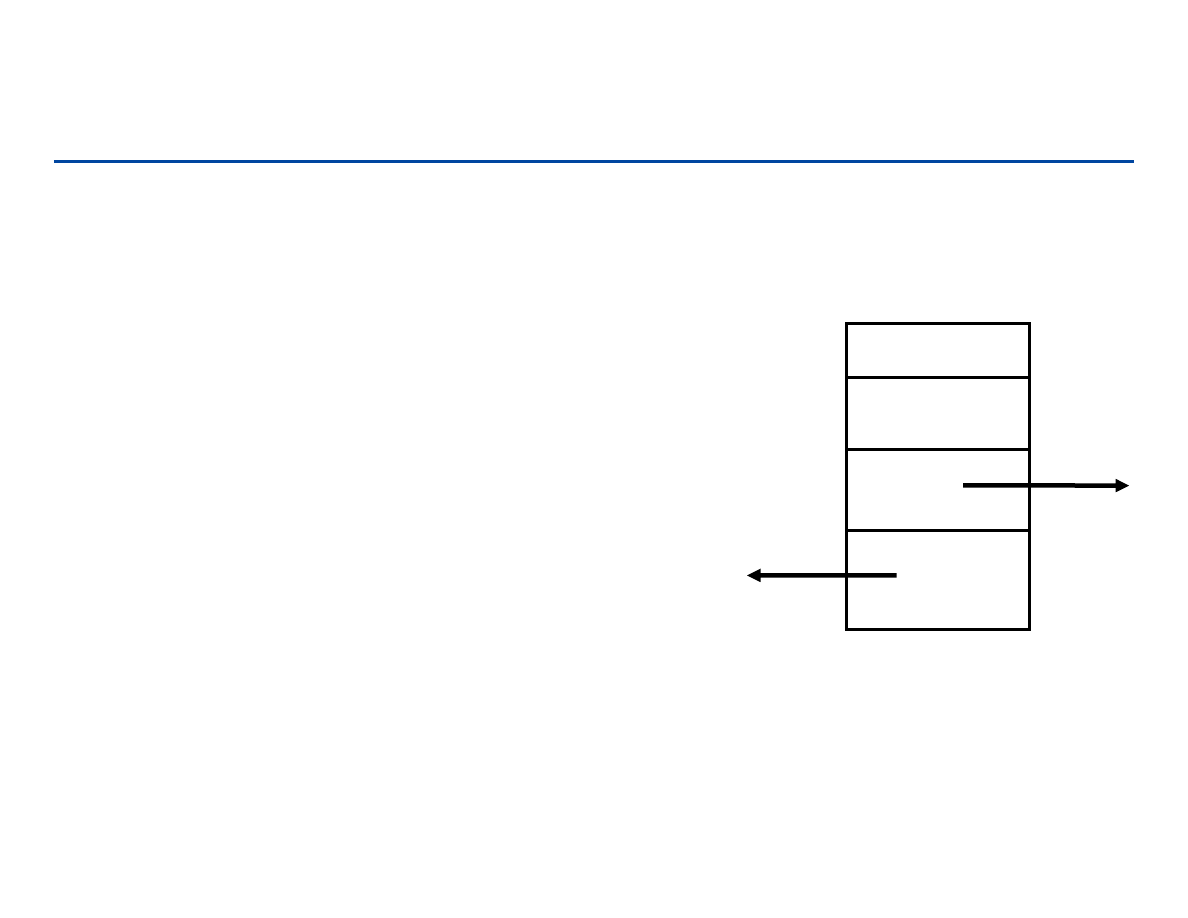
Listy łączone

Rozmieszczenie fizyczne obiektów w pamięci nie musi odpowiadać

ich logicznej kolejności; wykorzystujemy wskaźniki do obiektów (do

następnego/poprzedniego obiektu)

Manipulując wskaźnikami możemy dodawać, usuwać elementy do

listy bez przemieszczania pozostałych elementów listy

Lista taka może być pojedynczo lub podwójnie łączona.

a1

a2

an

a3

head

null

null

tail

…

181

Węzły i wskaźniki

Węzłem nazywać będziemy obiekt

przechowujący daną oraz wskaźnik do

następnej danej i (opcjonalnie – dla listy

podwójnie łączonej) wskaźnik do

poprzedniej danej. Jeśli nie istnieje

następny obiekt to wartość wskaźnika

będzie “null”

Wskaźnik oznacza adres obiektu w

pamięci

Węzły zajmują zwykle przestrzeń: Θ(1)

struct node {

key_type key;
data_type data;
struct node *next;
struct node *prev;

}

data

next

prev

key

182

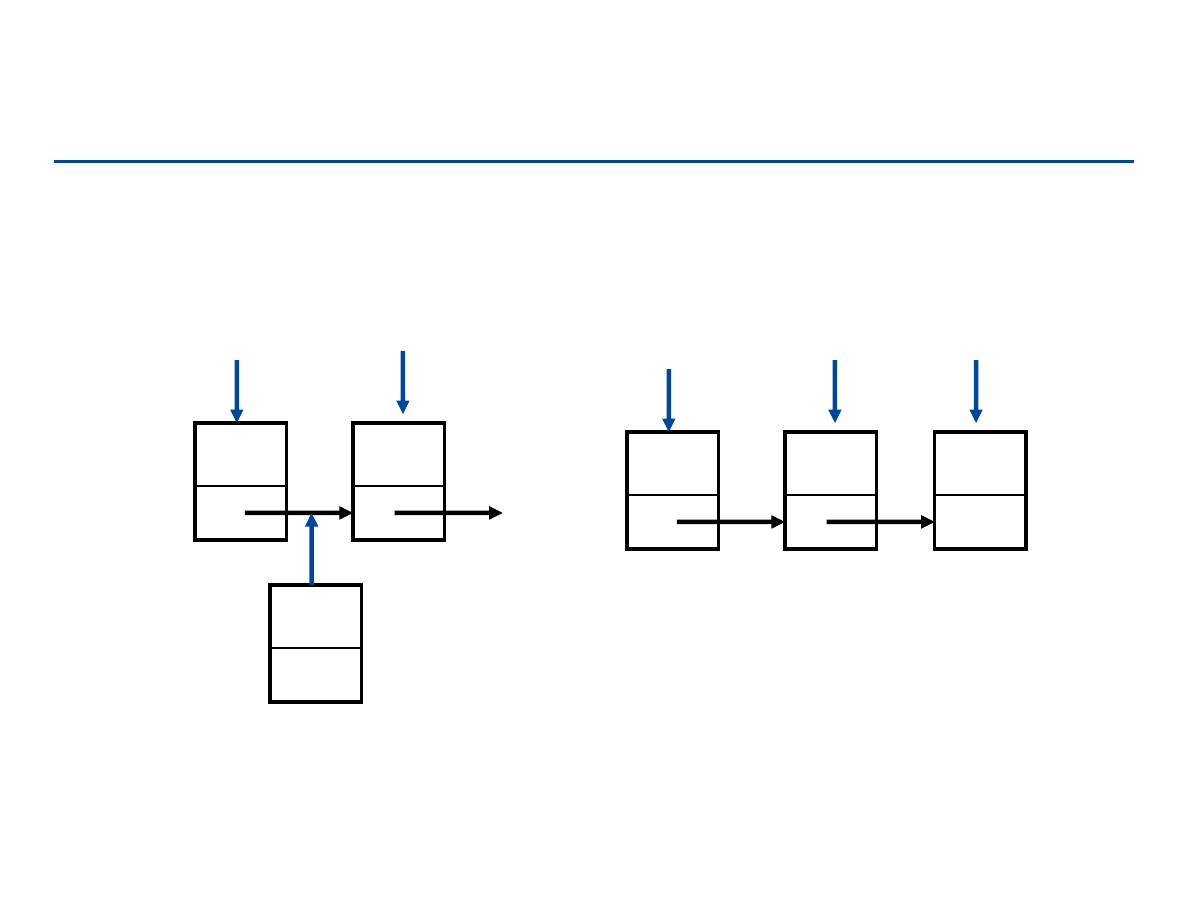
Wstawianie do listy (przykład operacji na liście)

wstawianie nowego węzła q pomiędzy węzły p i r:

a1

a3

p

r

a2

p

r

a1

a2

q

a3

next

[q]

r

next

[p]

q

183

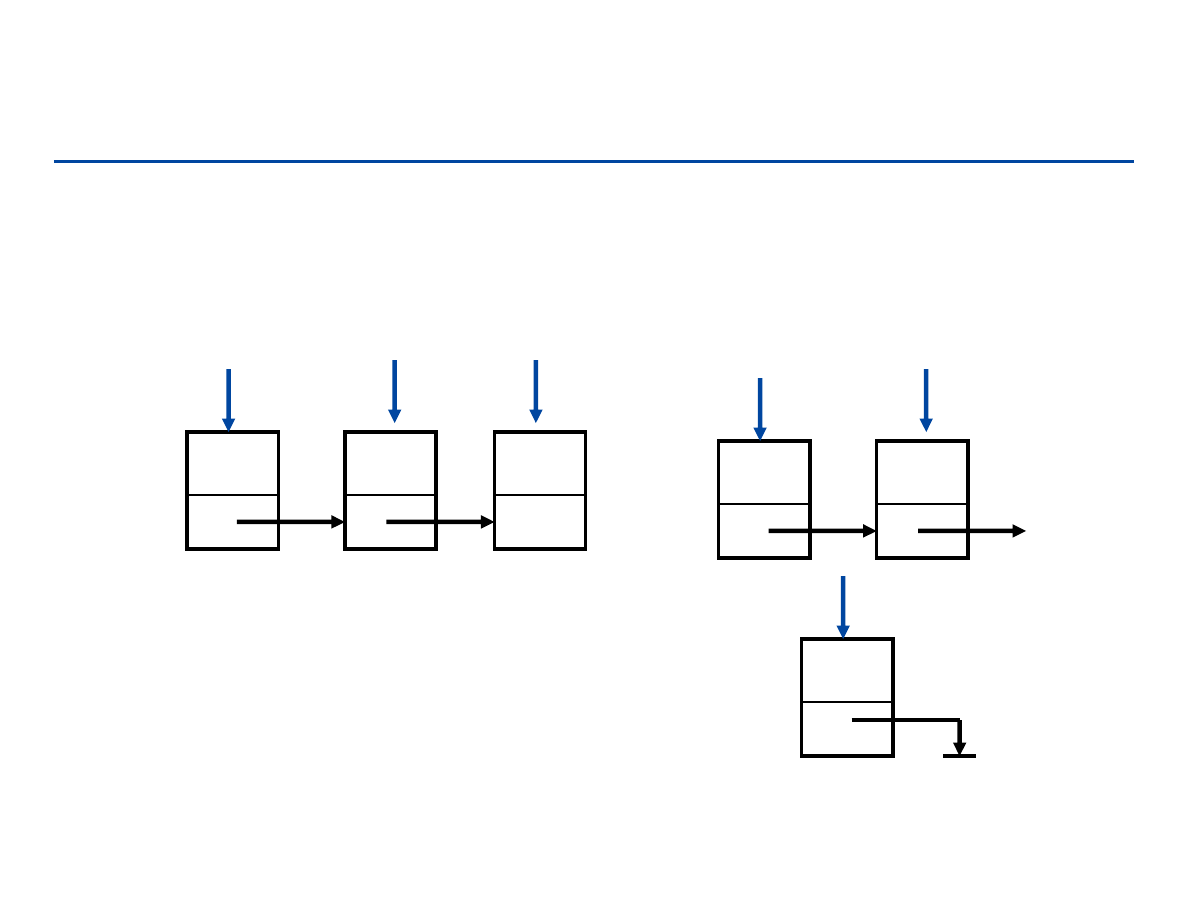
Usuwanie z listy

usuwanie węzła q

a1

a2

p

q

a3

r

a1

a3

p

r

next

[p]

r

next

[q]

null

a2

q

null

184

Operacje na liście łączonej

List-Search(L, k)
1.

x head[L]

2.

while x ≠ null and key[x] ≠ k

3.

do x next[x]

4.

return x

List-Insert(L, x)
1.

next[x] head[L]

2.

if head[L] ≠ null

3.

then prev[head[L]] x

4.

head[L] x

5.

prev[x]

null

List-Delete(L, x)
1.

if prev[L] ≠ null

2.

then next[prev[x]] next[x]

3.

else head[L] next[x]

4.

if next[L] ≠ null

5.

then prev[next[x]] prev[x]

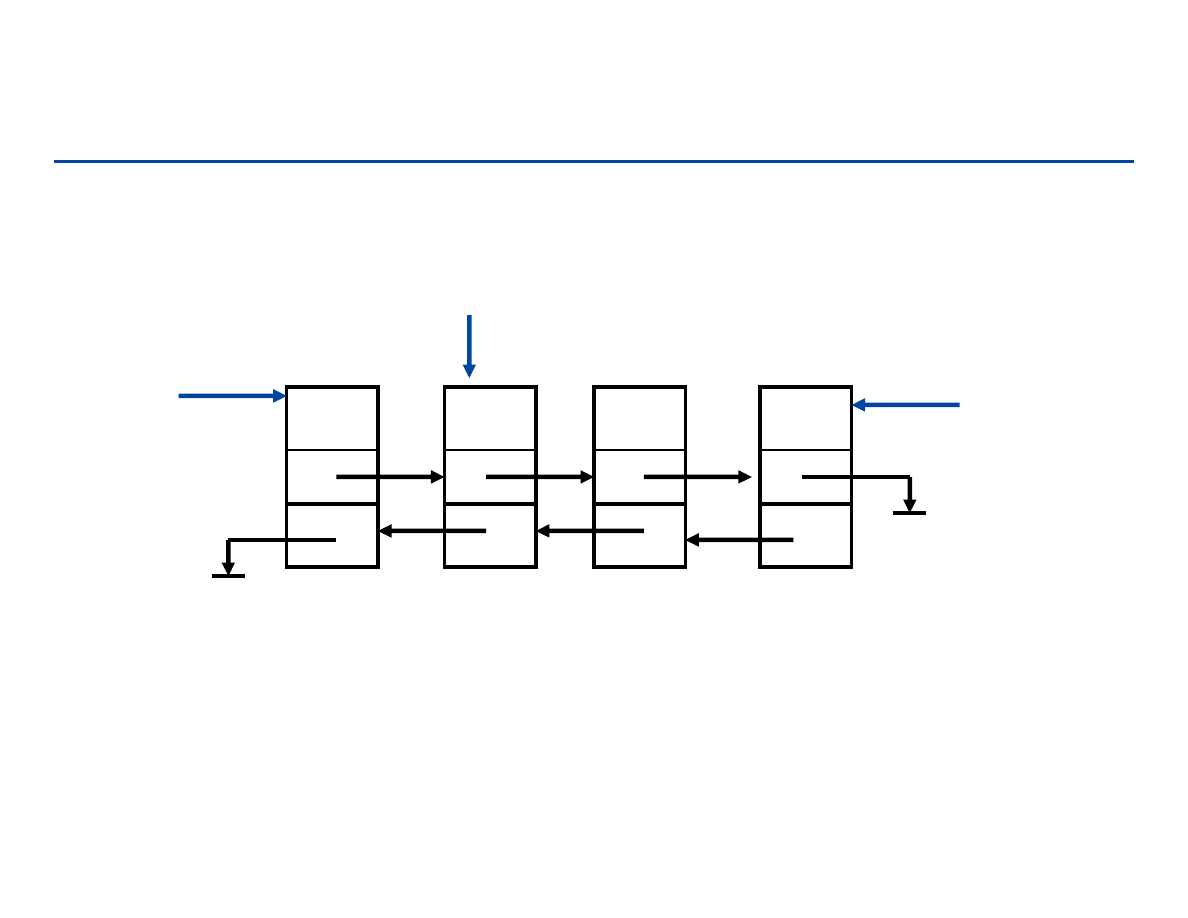
185

Listy podwójnie łączone

a1

a2

a4

a3

head

null

null

tail

x

Listy cykliczne: łączymy element pierwszy z ostatnim

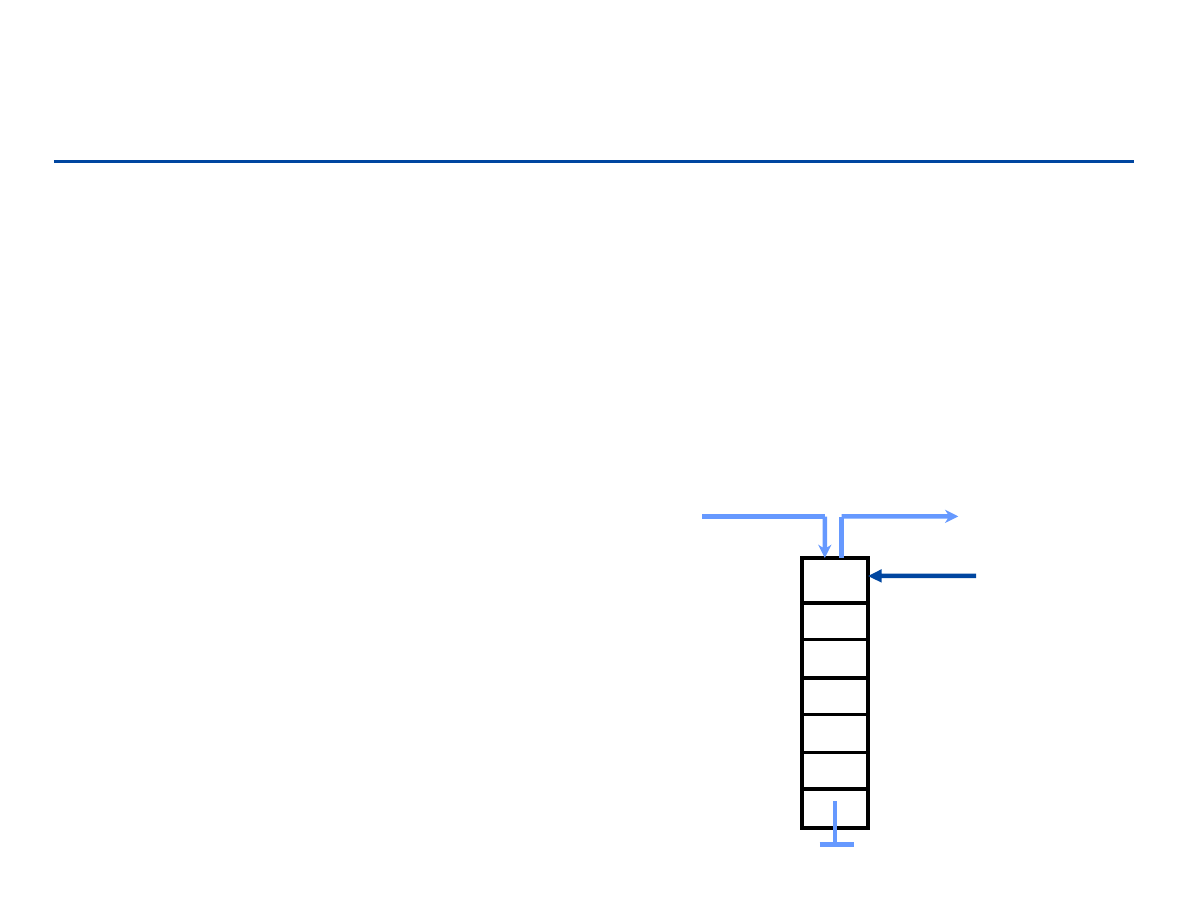
186

Stosem S nazywany liniową sekwencję elementów do której nowy

element x może zostać wstawiony jedynie na początek, analogicznie

element może zostać usunięty jedynie z początku tej sekwencji.

Stos rządzi się zasadą Last-In-First-Out (LIFO).

Operacje dla stosu:

– Stack-Empty(S)

– Pop(S)

– Push(S,x)

Stosy

Pop

Push

null

head

2
0
1
5

187

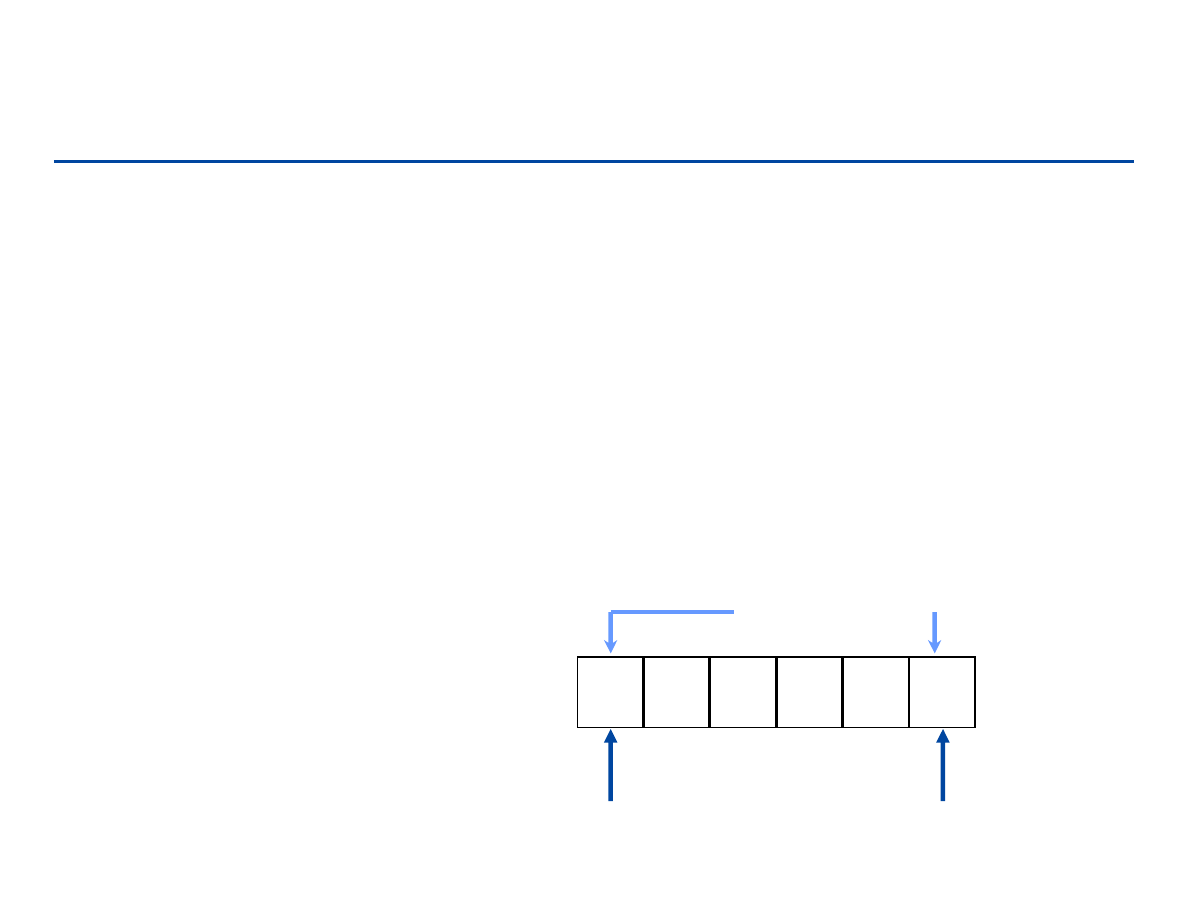
Kolejki

Kolejka Q jest to liniowa sekwencja elementów do której nowe

elementy wstawiane są na końcu sekwencji, natomiast elementy

usuwane są z jej początku.

Zasada First-In-First-Out (FIFO).

Operacje dla kolejki:

– Queue-Empty(Q)

– EnQueue(Q, x)

– DeQueue(Q)

2

2

0

3

0

1

head

tail

DeQueue

EnQueue

188

Implementacja stosu i kolejki

Tablicowa

– Wykorzystujemy tablicę A o n elementach A[i], gdzie n jest maksymalną

ilością elementów stosu/kolejki.

– Top(A), Head(A) i Tail(A) są indeksami tablicy

– Operacje na stosie/w kolejce odnoszą się do indeksów tablicy i elementów

tablicy

– Implementacja tablicowa nie jest efektywna

Listy łączone

– Nowe węzły tworzone są w miarę potrzeby

– Nie musimy znać maksymalnej ilości elementów z góry

– Operacje są manipulacjami na wskaźnikach

189

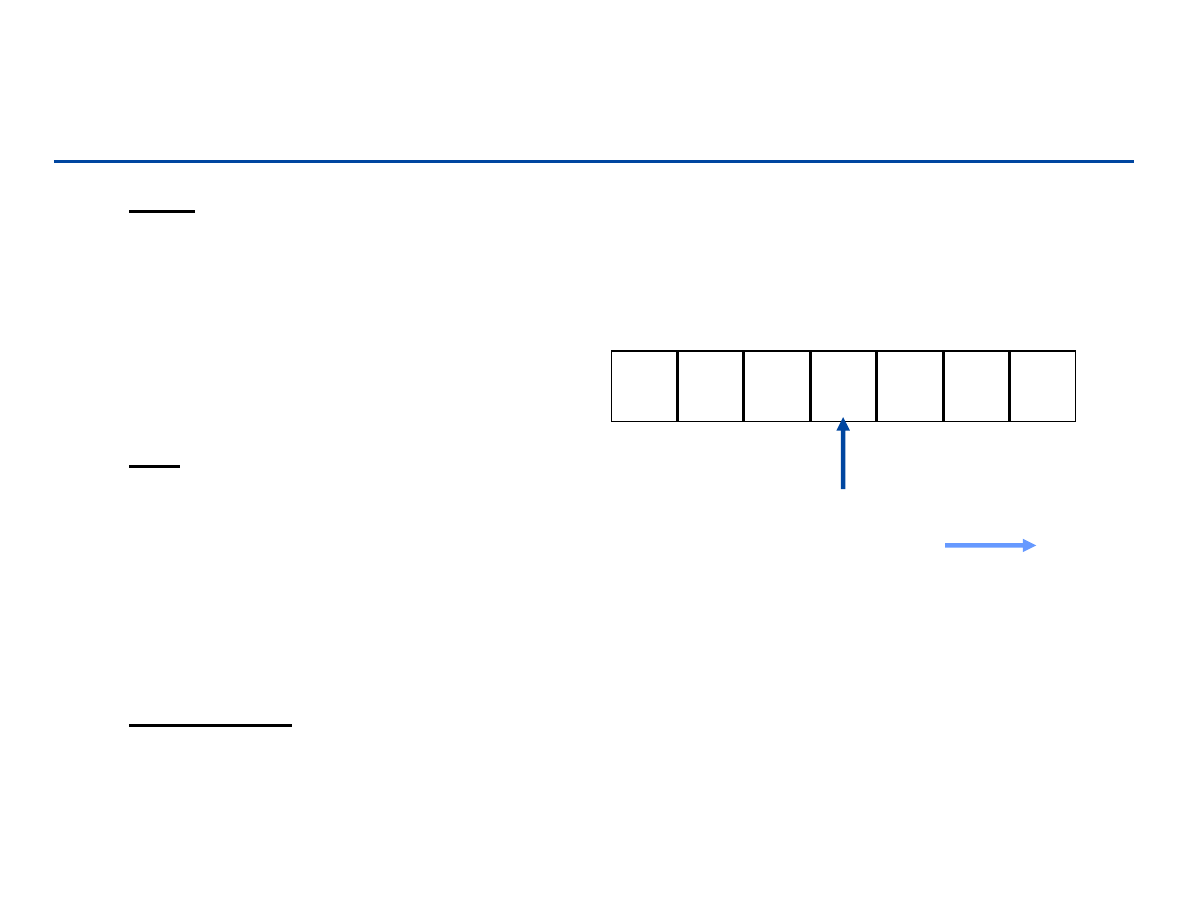
Implementacja tablicowa stosu

Push(S, x)
1.

if top[S] = length[S]

2.

then error “overflow”

3.

top[S] top[S] + 1

4.

S[top[S]] x

Pop(S)
1.

if top[S] = -1

2.

then error “underflow”

3.

else top[S] top[S] – 1

4.

return S[top[S] +1]

1

5

2

3

Kierunek

wstawiania

top

Stack-Empty(S)
1.

if top[S] = -1

2.

then return true

3.

else return false

0 1 2 3 4 5 6

190

Implementacja tablicowa kolejki

Enqueue(Q, x)
1.

Q[tail[Q]] x

2.

if tail[Q] = length[Q]

3.

then tail[Q] x

4.

else tail[Q] (tail[Q]+1)

mod n

Dequeue(Q)
1.

x Q[head[Q]]

2.

if head[Q] = length[Q]

3.

then head[Q] 1

4.

else head[Q] (head[Q]+1)

mod n

5.

return x

1

5

2

3

0

head

tail

191

Drzewa z korzeniem

Drzewem z korzeniem T nazywamy ADT dla którego elementy są

zorganizowane w strukturę drzewiastą.

Drzewo składa się z węzłów przechowujących obiekt oraz krawędzi

reprezentujących zależności pomiędzy węzłami.

W drzewie występują trzy typy węzłów: korzeń (root), węzły

wewnętrzne, liście

Własności drzew:

– Istnieje droga z korzenia do każdego węzła (połączenia)

– Droga taka jest dokładnie jedna (brak cykli)

– Każdy węzeł z wyjątkiem korzenia posiada rodzica (przodka)

– Liście nie mają potomków

– Węzły wewnętrzne mają jednego lub więcej potomków (= 2 binarne)

192

Drzewa z korzeniem

A

B

E

F

M

L

K

D

G

J

N

C

H

I

0

1

2

3

193

Terminologia

Rodzice (przodkowie) i dzieci (potomkowie)

Rodzeństwo (sibling) – potomkowie tego samego węzła

Relacja jest dzieckiem/rodzicem.

Poziom węzła

Ścieżka (path): sekwencja węzłów n

1

, n

2

, … ,n

k

takich, że n

i

jest

przodkiem n

i+1.

Długością ścieżki

nazywamy liczbę k.

Wysokość drzewa: maksymalna długość ścieżki w drzewie od korzenia

do liścia.

Głębokość węzła: długość ścieżki od korzenia do tego węzła.

194

Drzewa binarne

A

B

C

F

E

D

G

≠

A

B

C

F

E

D

G

Porządek węzłów

jest istotny!!!

Drzewem binarnym T nazywamy drzewo z korzeniem, dla którego

każdy węzeł ma co najwyżej 2 potomków.

195

Drzewa pełne i drzewa kompletne

Drzewo binarne jest pełne jeśli każdy węzeł wewnętrzny ma

dokładnie dwóch potomków.

Drzewo jest kompletne jeśli każdy liść ma tę samą głębokość.

A

B

C

E

D

G

F

A

B

C

E

D

G

F

pełne

kompletne

196

Własności drzew binarnych

Ilość węzłów na poziomie d w kompletnym drzewie binarnym wynosi

2

d

Ilość węzłów wewnętrznych w takim drzewie:

1+2+4+…+2

d–1

= 2

d

–1 (mniej niż połowa!)

Ilość wszystkich węzłów:

1+2+4+…+2

d

= 2

d+1

–1

Jak wysokie może być drzewo binarne o n liściach:

(n –1)/2

Wysokość drzewa

:

2

d+1

–1= n log (n+1) –1 ≤ log (n)

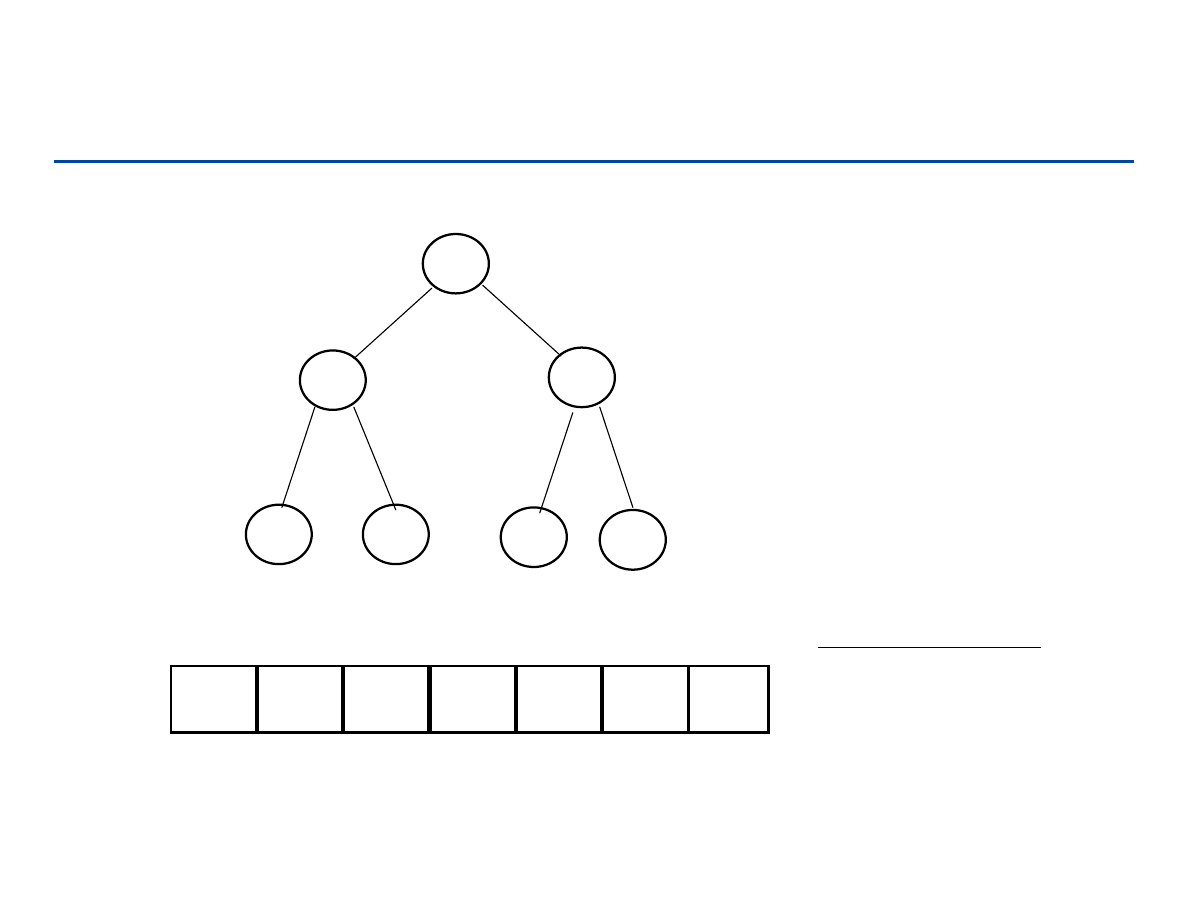
197

Tablicowa implementacja drzewa binarnego

A

B

C

E

D

G

F

1 2 3 4 5

6 7

2

0

2

1

2

2

A

B

D

C

E

F

G

0

1

2

2

Poziom

Na każdym poziomie d

mamy 2

d

elementów

Kompletne drzewo:
parent(i) = floor(i/2)
left-child(i) = 2i
right-child(i) = 2i +1

1

2

3

4

5

6

7

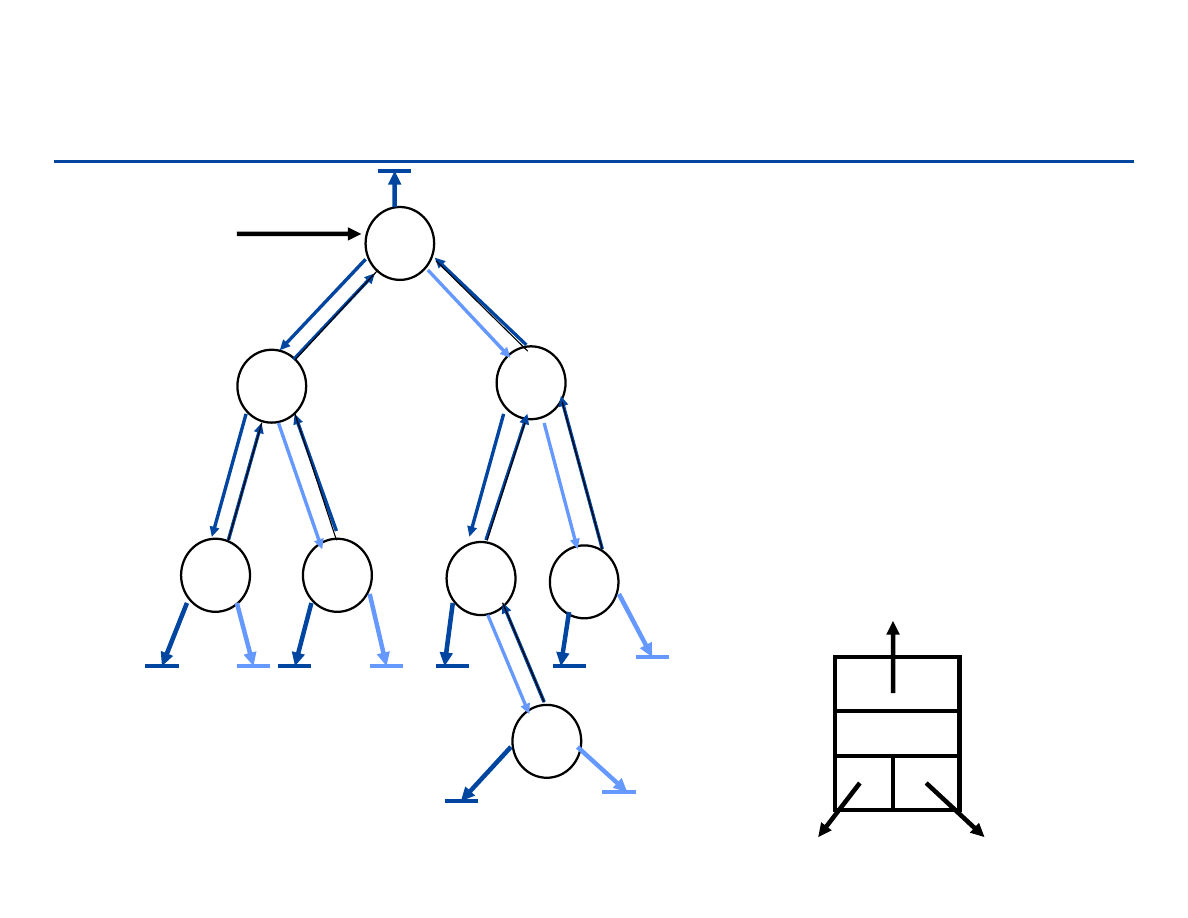
198

Listowa implementacja drzewa binarnego

A

B

C

E

D

G

F

H

Każdy węzeł zawiera
Dane oraz 3 wskaźniki:
•

przodek

•

lewy potomek

•

prawy potomek

root

(T)

data

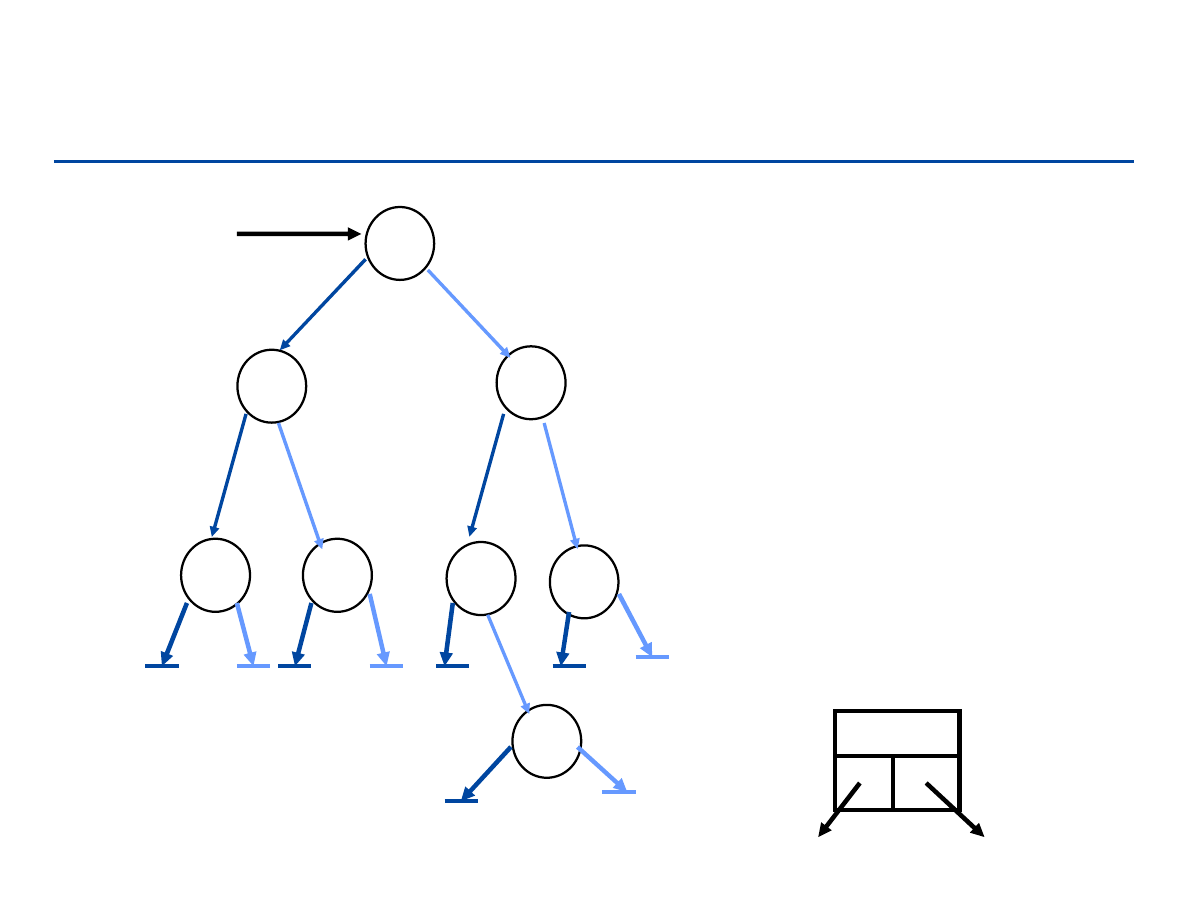
199

Listowa implementacja drzewa binarnego (najprostsza)

A

B

C

E

D

G

F

H

Każdy węzeł zawiera
Dane oraz 2 wskaźniki:
•

lewy potomek

•

prawy potomek

root

(T)

data

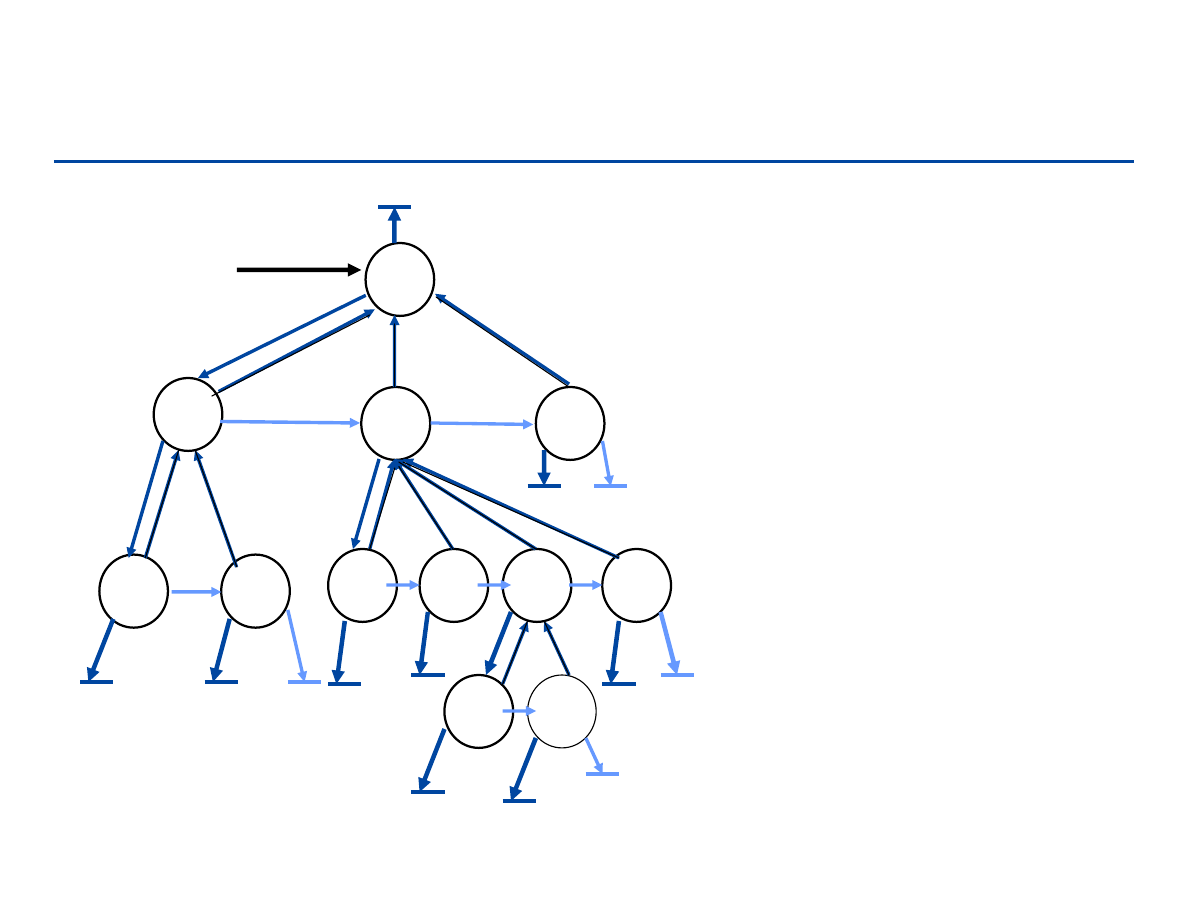
200

Listowa implementacja drzewa (n-drzewa)

A

B

D

E

D

G

Każdy węzeł zawiera
Dane oraz 3 wskaźniki:
•

przodek

•

lewy potomek

•

prawe rodzeństwo

C

root

(T)

F

H

I

J

K

201

Drzewa poszukiwań

binarnych (BST)

202

O czym będziemy mówić

Definicja
Operacje na drzewach BST:

– Search

– Minimum, Maximum

– Predecessor, Successor

– Insert, Delete

Struktura losowo budowanych drzew BST

203

Wprowadzenie

Poszukujemy dynamicznego ADT, który efektywnie będzie obsługiwał

następujące operacje:

– Wyszukiwanie elementu (Search)

– Znajdowanie Minimum/Maximum

– Znajdowanie poprzednika/następnika (Predecessor/Successor)

– Wstawianie/usuwanie elementu (Insert/Delete)

Wykorzystamy drzewo binarne! Wszystkie operacje powinny zajmować

czas Θ(lg n)

Drzewo powinno być zawsze zbalansowane – inaczej czas będzie

proporcjonalny do wysokości drzewa (gorszy od O(lg n))!

204

Drzewo poszukiwań binarnych (binary search tree)

Struktura drzewa z korzeniem

Każdy węzeł x posiada pola left(x), right(x), parent(x), oraz key(x).

Własność drzewa BST:

Niech x będzie dowolnym węzłem drzewa, natomiast niech y będzie

należał do poddrzewa o korzeniu w x wtedy:.

– Jeżeli należy do lewego poddrzewa to: key(y) ≤ key(x)

– Jeżeli należy do prawego poddrzewa to : key(y)

> key(x)

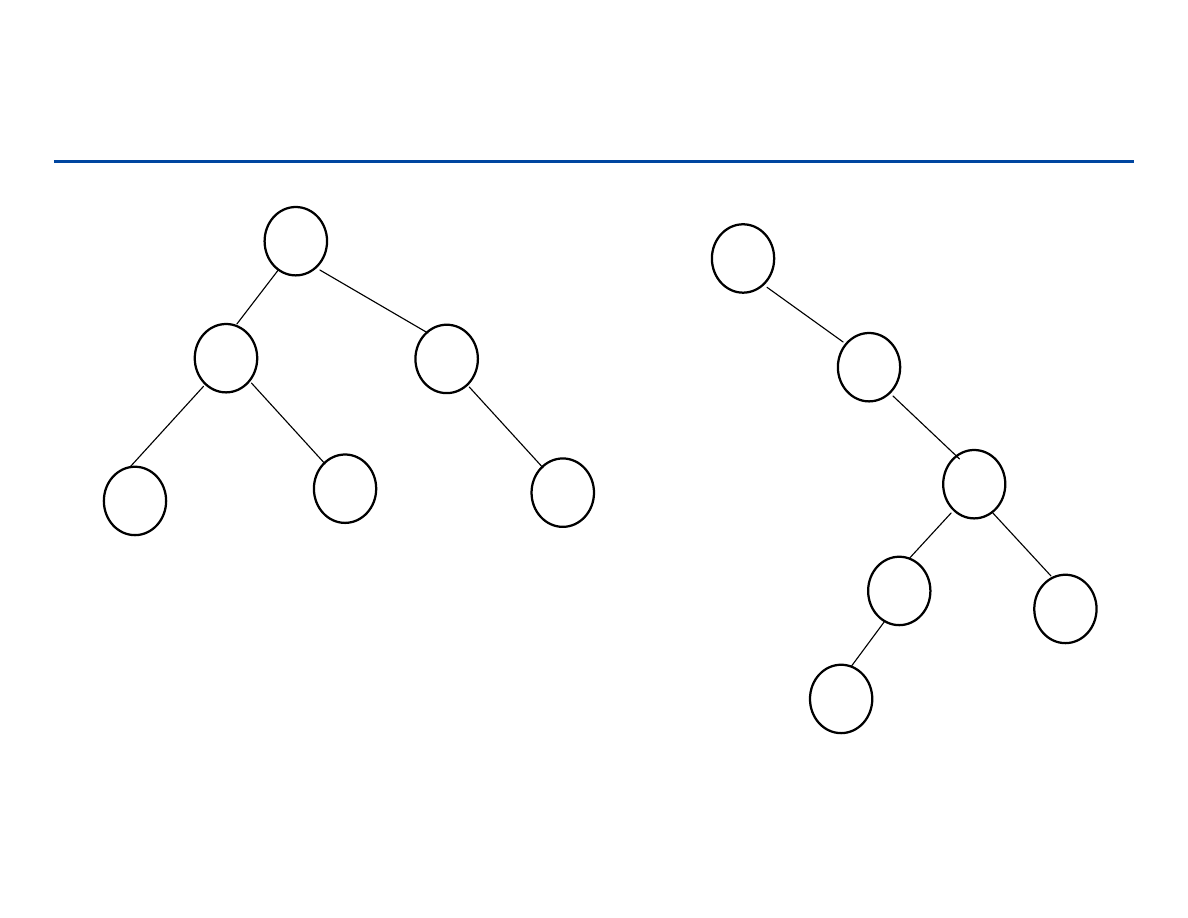
205

Przykład BST

5

3

5

5

7

8

2

3

7

2

8

5

Metody przechodzenia przez drzewo :

In-order, pre-order, post-order

206

Tree-Search

(x,k)

if

x = null or k = key[x]

then return

x

if

k < key[x]

then return

Tree-Search(left[x],k)

else return

Tree-Search(right[x],k)

Tree-Search

(x,k)

while

x ≠ null and k ≠ key[x]

do if

k < key[x]

then

x

left[x]

else

x

right[x]

return

x

Poszukiwanie w drzewie BST

rekurencyjnie

iteracyjnie

złożoność: O(h)

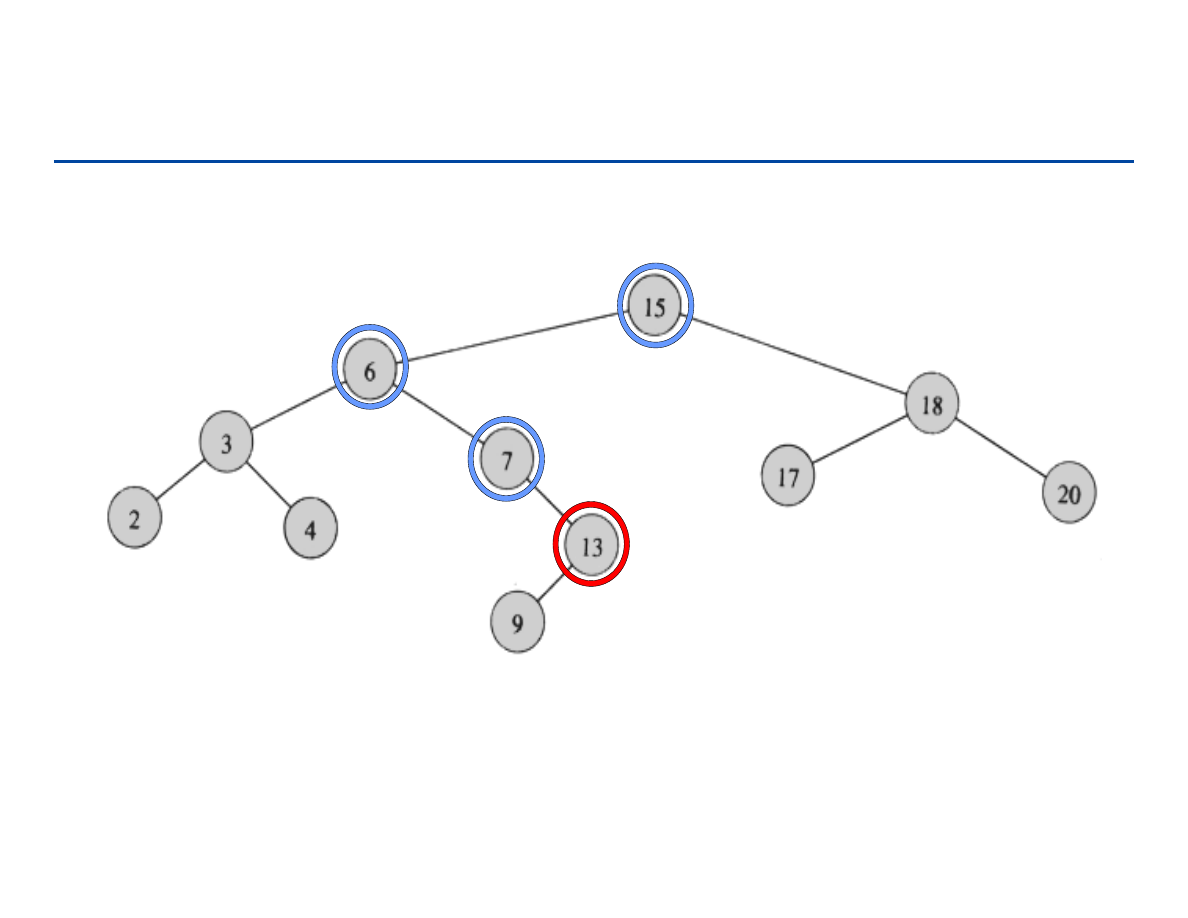
207

Przykład

Poszukiwany klucz: 13

208

Przechodzenie przez wszystkie węzły drzewa

Inorder-Tree-Walk(x)

if x ≠ null

then Inorder-Tree-Walk(left[x])

print key[x]
Inorder-Tree-Walk(right[x])

złożoność: Θ(n)

czas wykonania:

T(0) = Θ(1)

T(n)=T(k) + T(n – k –1) + Θ(1)

209

Tree-Minimum

(x)

while

left[x] ≠ null

do

x

left[x]

return

x

Tree-Maximum

(x)

while

right[x] ≠ null

do

x

right[x]

return

x

Odnajdowanie minimum i maksimum

złożoność: O(h)

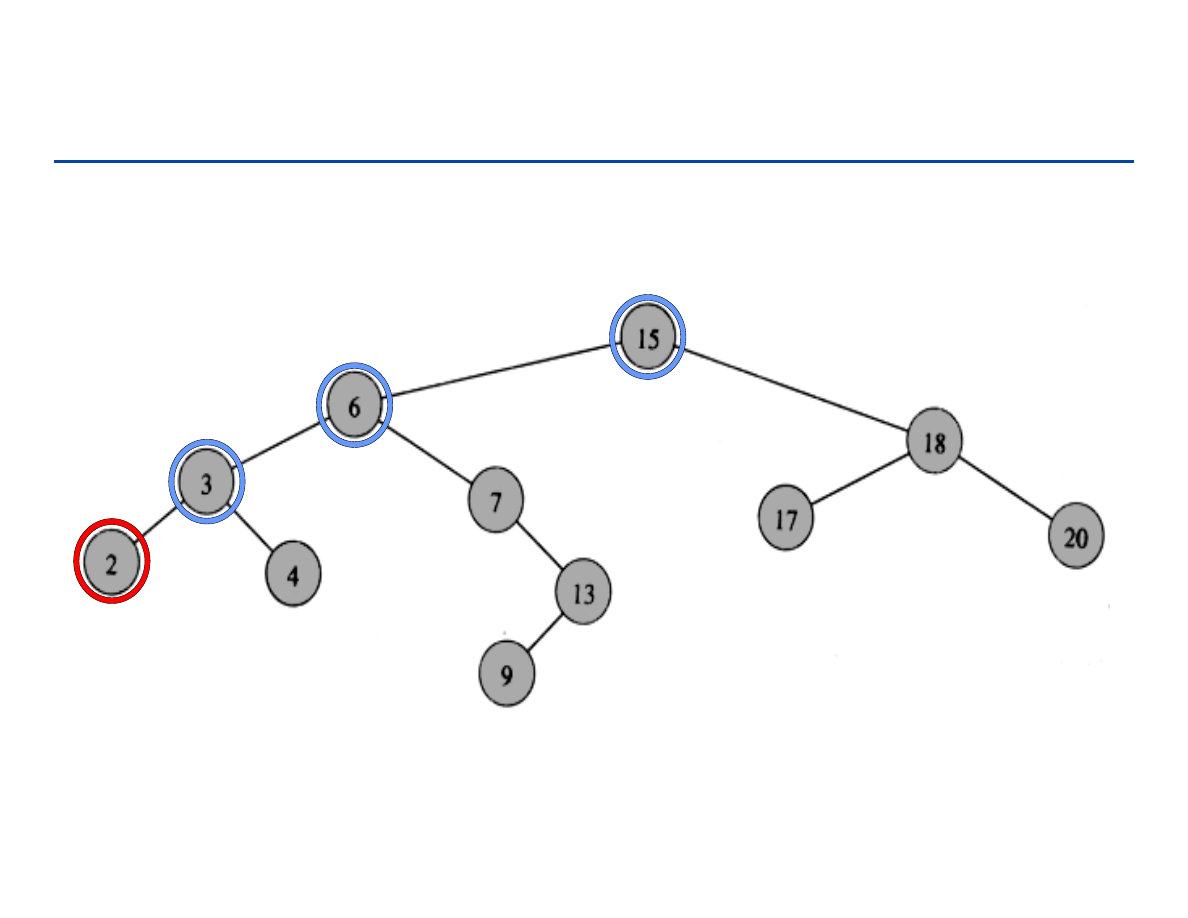
210

Przykład – minimum

211

Odnajdowanie następnika

Następnikiem x nazywamy najmniejszy element y wśród elementów
większych od x

Następnik może zostać odnaleziony bez porównywania kluczy. Jest
to :

1.

null jeśli x jest największym z węzłów.

2.

minimum w prawym poddrzewie t jeśli ono istnieje.

3.

najmniejszy z przodków x, dla których lewy potomek jest
przodkiem x.

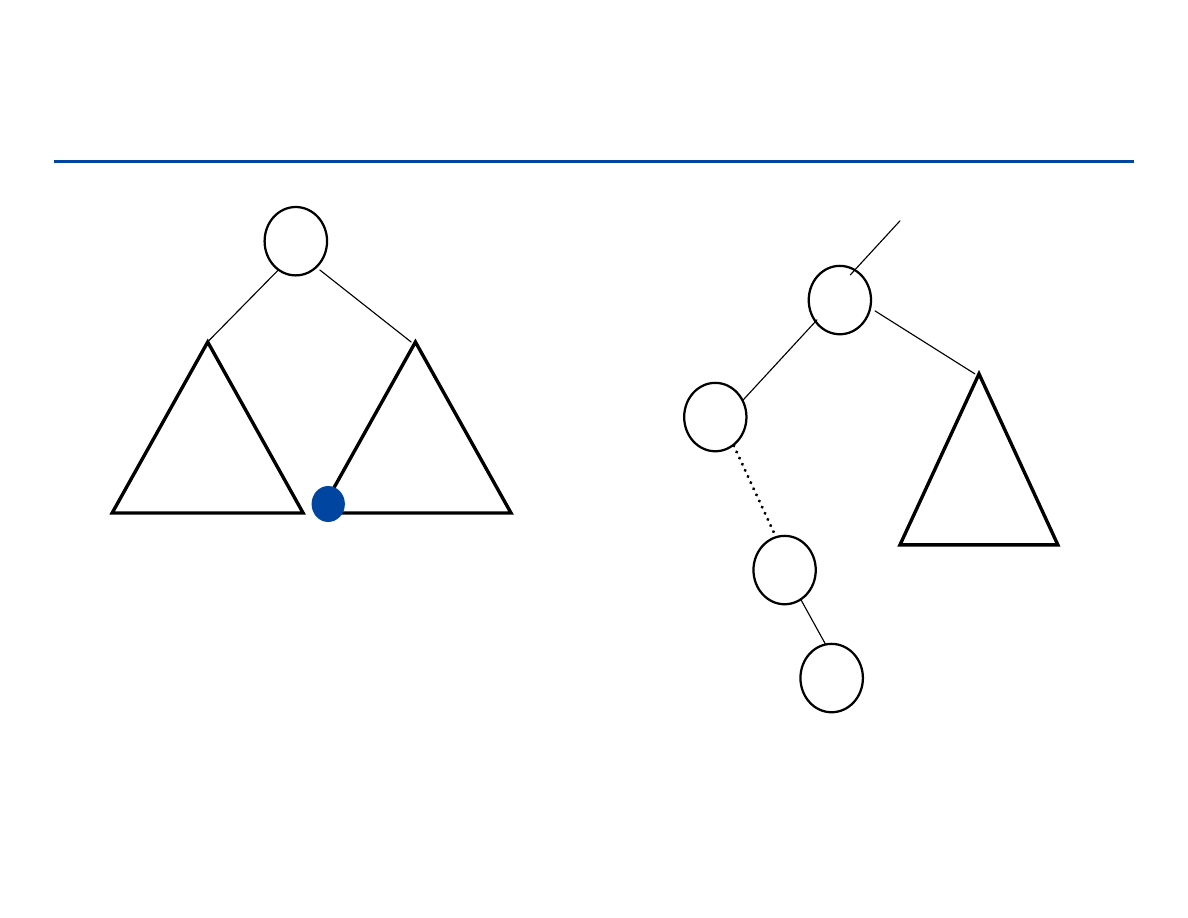
212

Odnajdowanie następnika

x

minimum w prawym poddrzewie t

y

z

x

najmniejszy z przodków x,

dla których lewy potomek

jest przodkiem x

213

Odnajdowanie następnika

Tree-Successor(x)

if right[x] ≠ null

// przypadek 2

then return Tree-Minimum(right[x])
y parent[x]

while y ≠ null and x = right[y]

// przypadek 3

do x y

y parent[y]

return y

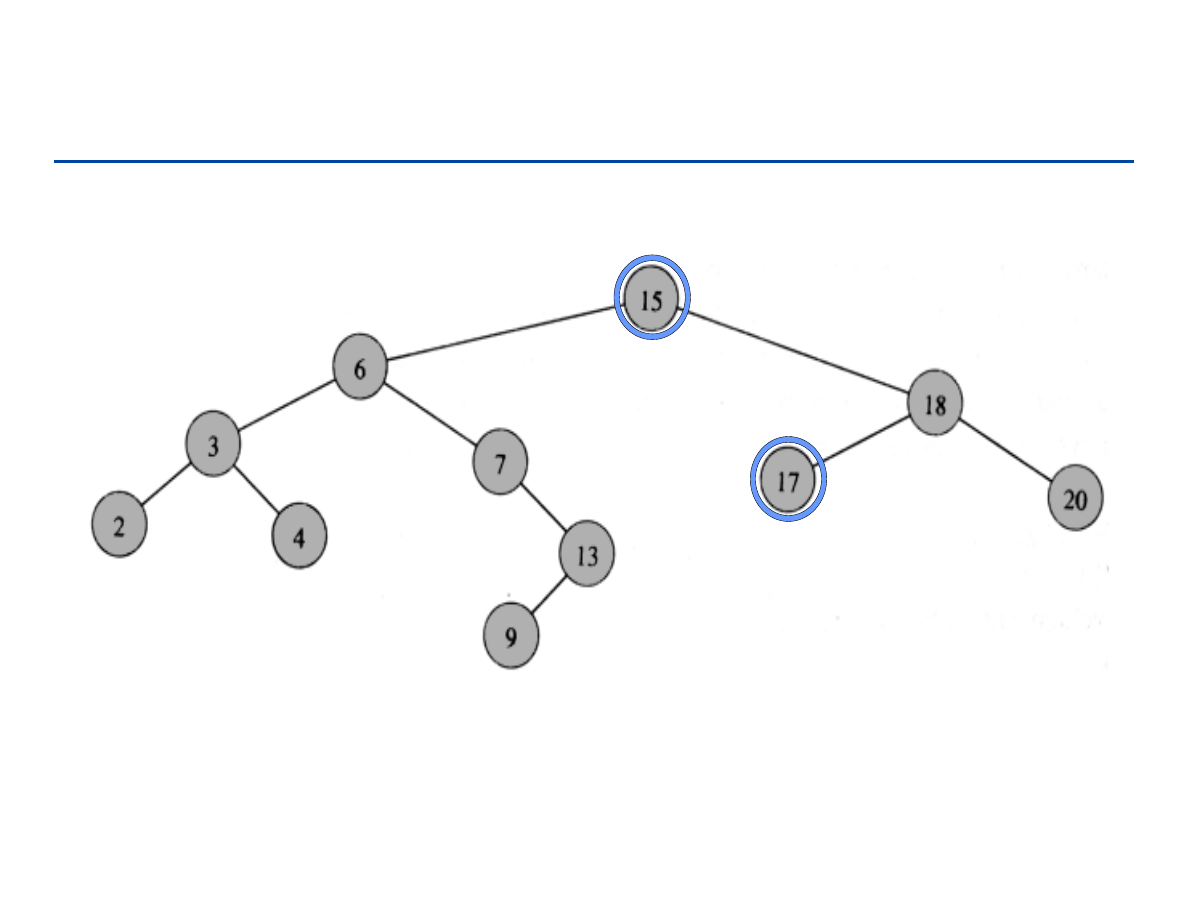
214

Przykład

Poszukajmy następników dla 15 (przyp. 2), 13 (przyp. 3)

215

Wstawianie elementów

Wstawianie jest bardzo zbliżone do odnajdowania elementu:

– Odnajdujemy właściwe miejsce w drzewie, w które chcemy wstawić

nowy węzeł z.

Dodawany węzeł z zawsze staje się liściem.

Zakładamy, że początkowo left(z) oraz right(z) mają wartość null.

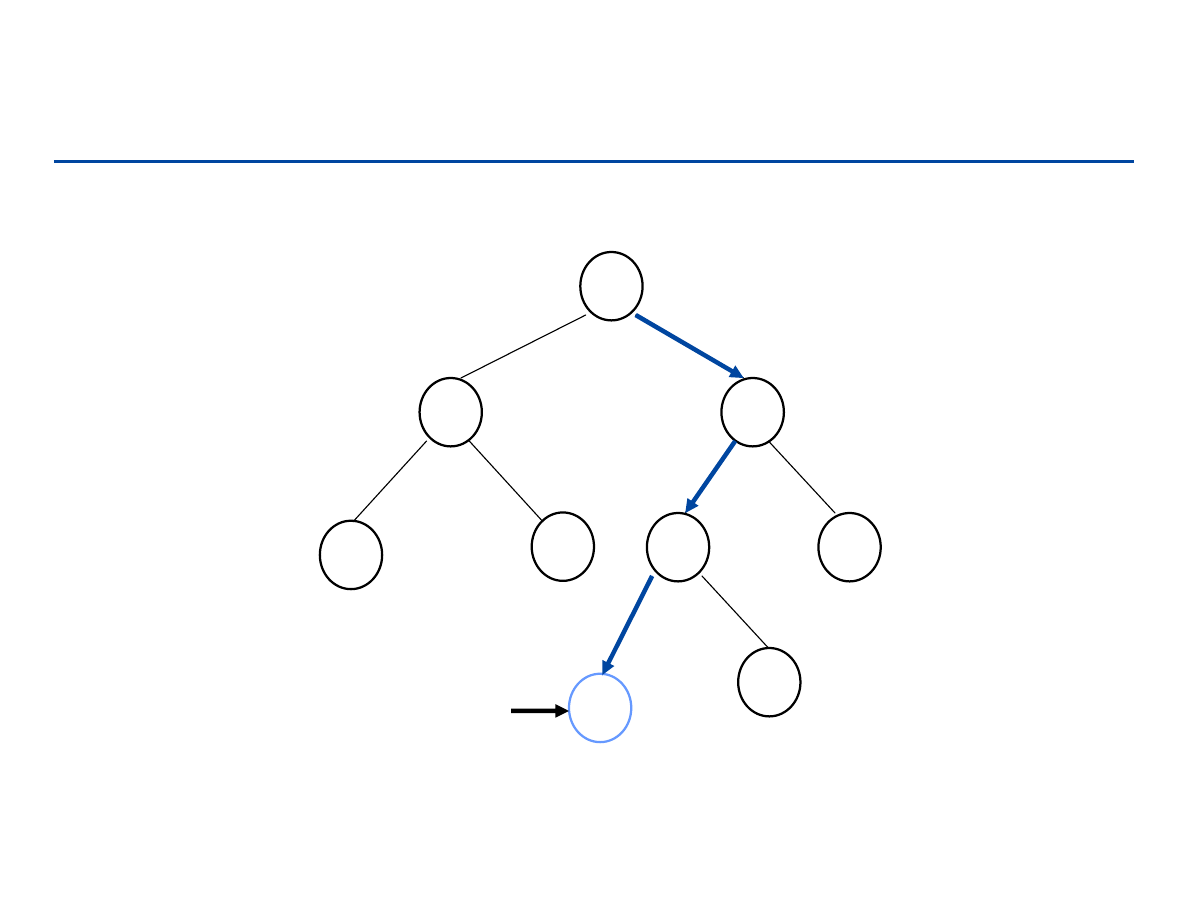
216

Wstawanie – przykład

12

5

9

18

19

15

17

2

13

Wstawiamy 13 do drzewa

z

217

Wstawianie – pseudokod

Tree-Insert(T,z)
y null
x root[T]
while x ≠ null

do y x

if key[z] < key[x]

then x left[x]
else x right[x]

parent[z] y

// dla pustego drzewa
if y = null then root[T] z
else if key[z] < key[y]

then left[y] z
else right[y] z

218

Usuwanie z drzewa BST

Usuwanie elementu jest bardziej skomplikowane niż wstawianie. Można

rozważać trzy przypadki usuwania węzła z:

1.

z nie ma potomków

2.

z ma jednego potomka

3.

z ma 2 potomków

przypadek 1: usuwamy z i zmieniamy u rodzica wskazanie na null.

przypadek 2: usuwamy z a jego dziecko staje się dzieckiem rodzica.

przypadek 3:najbardziej złożony; nie można po prostu usunąć węzła i

przenieść dzieci do rodzica – drzewo przestałoby być binarne!

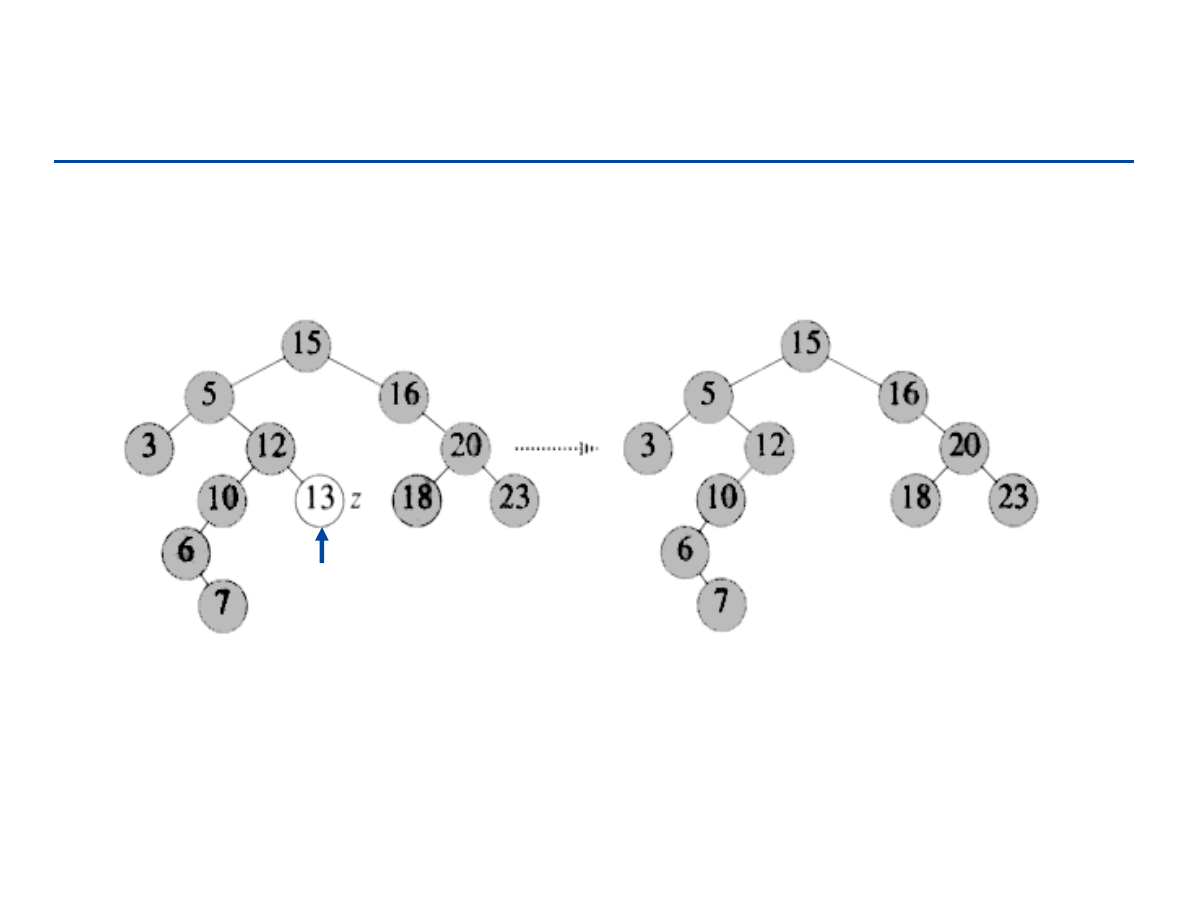
219

delete

Usuwanie z drzewa BST - przypadek 1

usuwamy

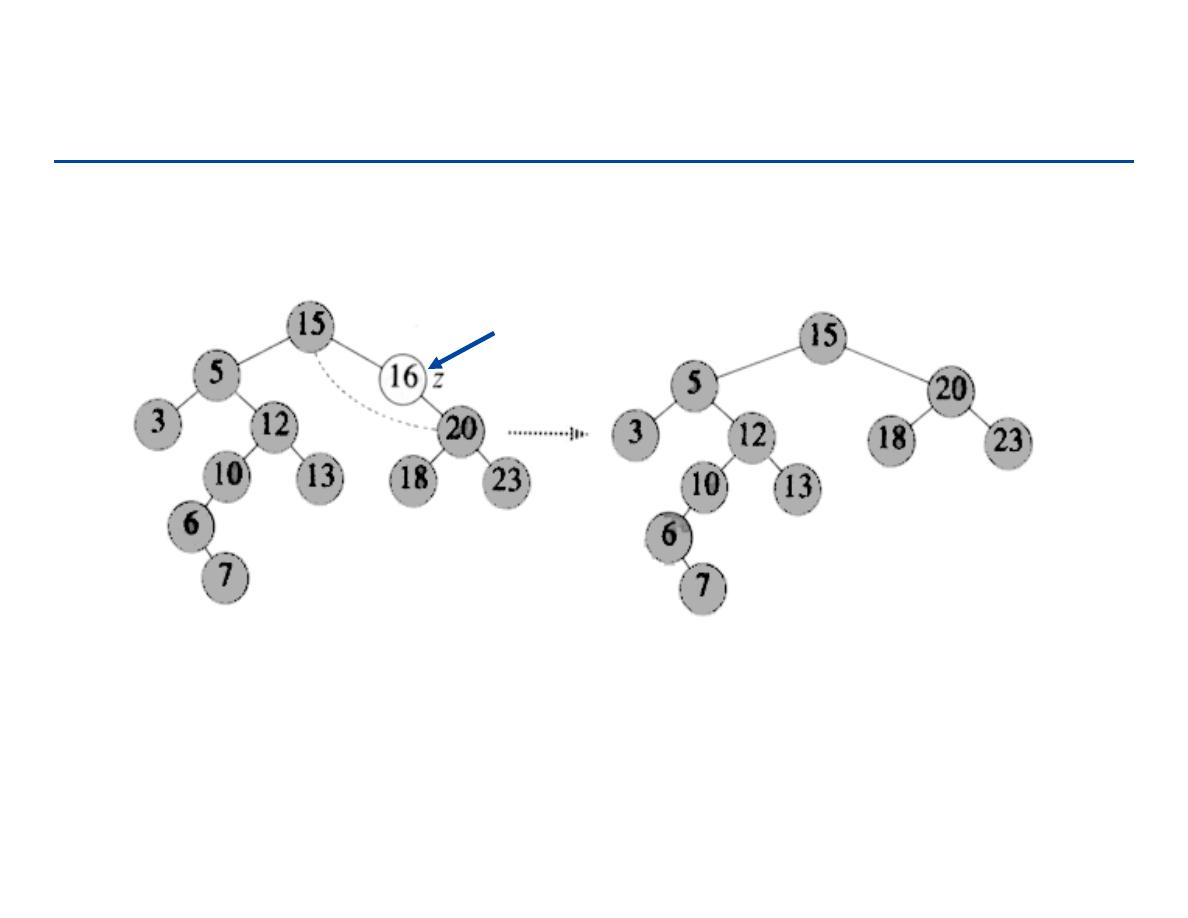
220

Usuwanie z drzewa BST przypadek 2

Usuwany

węzeł

221

Usuwanie z drzewa BST

przypadek 3

Rozwiązanie polega na zastąpieniu węzła jego następnikiem.

założenie: jeśli węzeł ma dwóch potomków, jego następnik ma co

najwyżej jednego potomka.

dowód: jeśli węzeł ma 2 potomków to jego następnikiem jest minimum z

prawego poddrzewa. Minimum nie może posiadać lewego potomka

(inaczej nie byłoby to minimum)

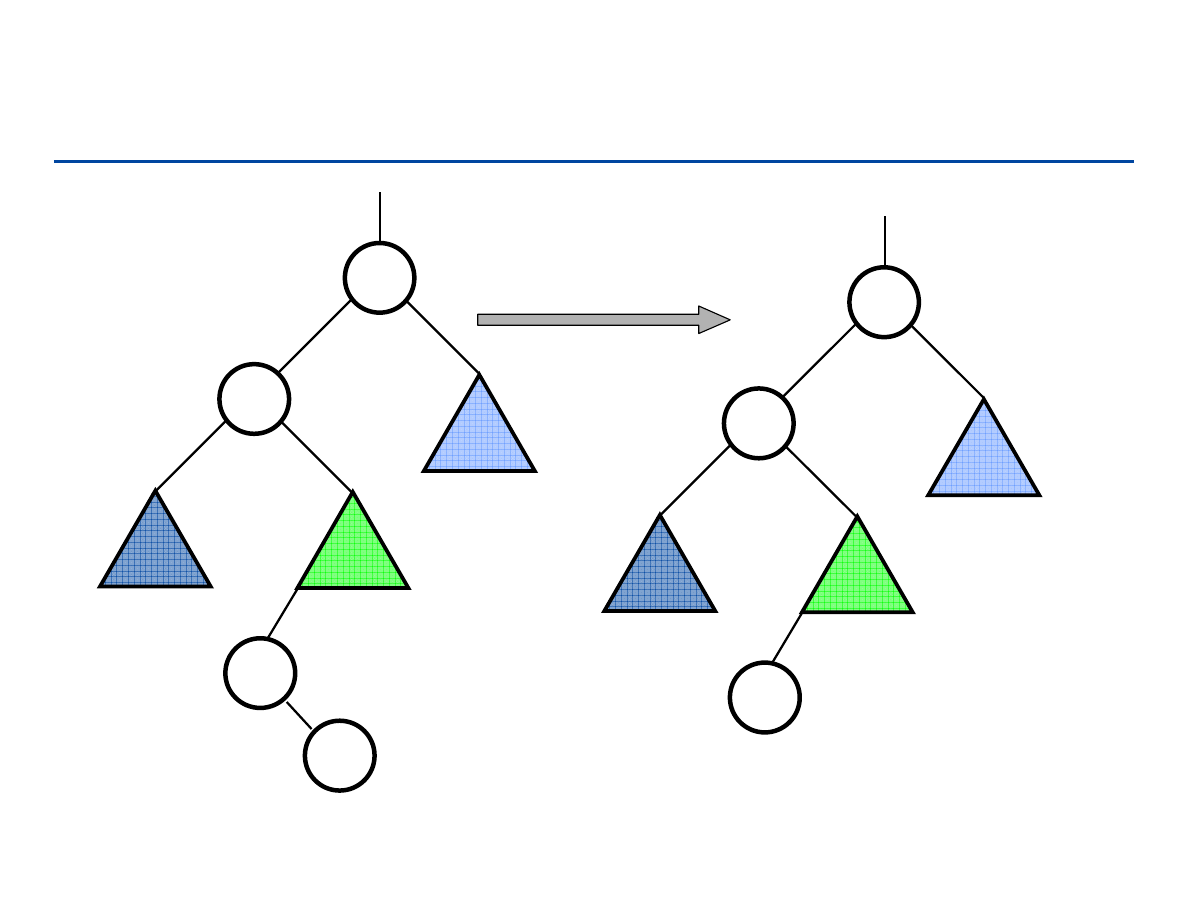
222

Usuwanie z drzewa BST – przypadek 3

z

α

β

δ

Usuwamy

z

y

w

y

α

β

δ

w

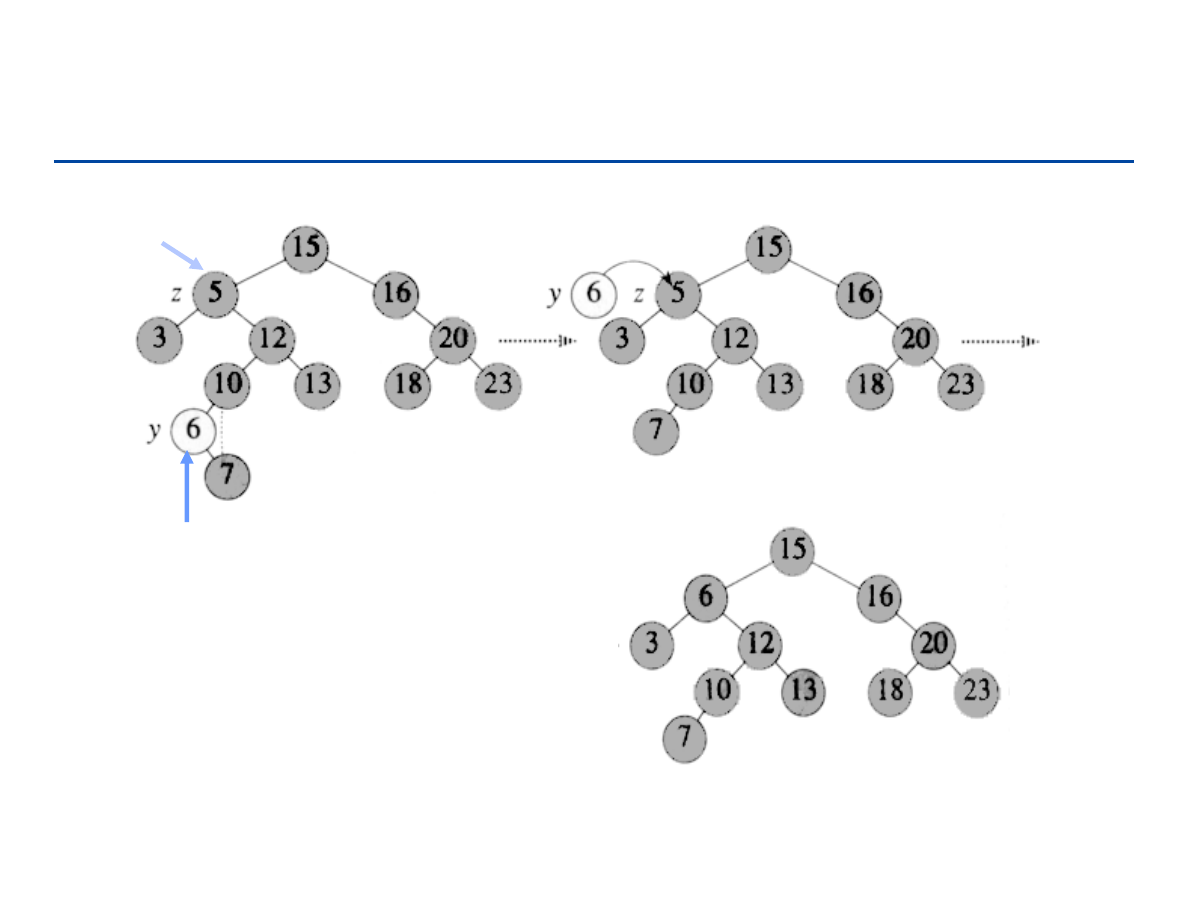
223

Usuwanie z drzewa BST – przypadek 3

usuwamy

następnik

224

Usuwanie z drzewa BST – pseudokod

Tree-Delete

(T,z)

if

left[z] = null or right[z] = null /* p. 1 lub 2

then

y

z

else

y

Tree-Successor(z)

if

left[y] ≠ null

then

x

left[y]

else

x

right[y]

if

x ≠ null

then

parent[x]

parent[y]

if

parent[y] = null

then

root[T]

x

else if

y = left[parent[y]]

then

left[parent[y]]

x

else

right[parent[y]]

x

if y ≠ z

then key[z] key[y]

return y

225

Analiza złożoności

Usuwanie: dwa pierwsze przypadki wymagają O(1) operacji: tylko

zamiana wskaźników.

Przypadek 3 wymaga wywołania Tree-Successor, i dlatego wymaga

czasu O(h).

Stad wszystkie dynamiczne operacje na drzewie BST zajmują czas O(h),

gdzie h jest wysokością drzewa.

W najgorszym przypadku wysokość ta wynosi O(n)