1
Wprowadzenie do Teorii Algorytmów
(Introduction to Algorithms Theory)
Prof. Dr hab. Alexander Prokopenya
Szkoła Główna Gospodarstwa Wiejskiego w Warszawie
Katedra Zastosowań Informatyki
Wykład 9-10.
Algorytmy zachłanne
Algorytmy zachłanne budują rozwiązanie problemu krok po kroku, zawsze wybie-
rając jako kolejny krok ten, który jest najbardziej oczywisty, który oferuje natychmiast o-
we korzyści. Chociaż takie podejście może być zgubne dla niektórych zadań, istnieje wi e-
le problemów, dla których daje rozwiązanie optymalne. Naszym pierwszym przykładem
będzie szukanie minimalnego drzewa rozpinającego.
1. Minimalne drzewo rozpinające
Wyobraź sobie, że zostałeś poproszony o zaprojektowanie sieci komputerowej łączącej wybrane
pary komputerów z danego zbioru. Przekładając tę sytuację na problem grafowy: każdy wierz-
chołek jest komputerom, nieskierowana krawędź potencjalnym połączeniem, a celem jest wy-
branie wystarczającej liczby krawędzi, aby wszystkie wierzchołki zostały połączone. Ale to nie
wszystko; każde połączenie ma swój koszt odzwierciedlony przez wagę krawędzi. Jaka jest moż-
liwa najtańsza sieć?
Spostrzegamy od razy, że optymalny zbiór krawędzi nie może tworzyć cyklu, ponieważ
usunięcie krawędzi z cyklu spowodowałoby zmniejszenie kosztu, nie naruszając spójności.
Własność 1. Usunięcie krawędzi cyklu nie rozspójnia grafu.
Szukany graf musi więc być spójny i acykliczny: nieskierowany graf tego typu nazywa-
my drzewem. Drzewo, którego szukamy, powinno mieć szczególną własność, mianowicie, naj-
mniejszą możliwą sumaryczną wagę krawędzi. Takie drzewo zwane jest minimalnym drzewem
rozpinającym (ang. minimum spanning tree, MST). Poniżej przegstawiamy formalną definicję
naszego problemu.
Wejście: nieskierowany graf
)
,
(
E
V
G
, wagi krawędzi
e
w .
Wyjście: drzewo
)
'
,
(
E
V
T
,
E
E
'
, takie że minimalizuje wagę:
'
)
(
E
e
e
w
T
waga
.
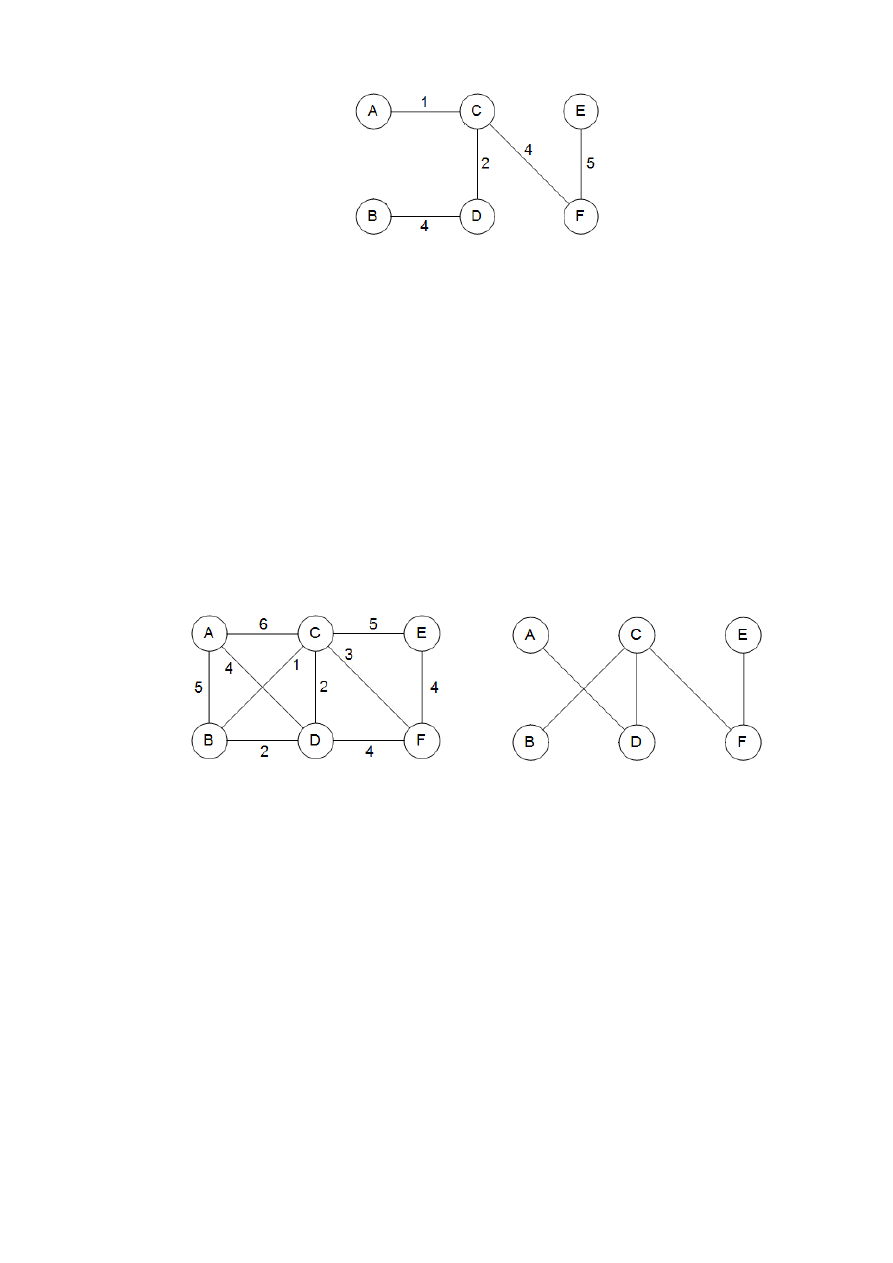
Minimalne drzewo rozpinające dla poprzedniego przykładu ma koszt równy 16:
2
Nie jest to jednak jedyne optymalne rozpiązanie.
1.1. Podejście zachłanne
Algorytm Kruskala znajdowania minimalnego drzewa rozpinającego zaczyna od pustego grafu i
wybiera krawędzie ze zbioru E według następującej zasady:
Dodawaj kolejno krawędzie najlżejsze spośród tych, które nie tworzą cykli.
Innymi słowy, algorytm konstruuje drzewo krawędź po krawędzi, uważając, aby nie powstał
cykl, i dodając krawędź najtańszą w danym momencie. Jest to algorytm zachłanny: każda po-
wzięta decyzja jest tą, która jest w danej chwili najkorzystniejsza.
Na rys. 1 jest podany przykład. Zaczynamy z grafem pustym i przeglądamy krawędzie w
kolejności rosnących wag (krawędzie o tej samej wadze są analizowanr w kolejności dowolnej):
C
B
,
D
C
,
D
B
,
F
C
,
F
D
,
F
E
,
D
A
,
B
A
,
E
C
,
C
A
.
Pierwsze dwie krawędzie dodajemy, trzecia, B-D , dodana do grafu tworzyłaby cykl. Ignorujemy
ją więc i idziemy dalej. Uzyskane drzewo ma koszt 14, jest to koszt możliwie najmniejszy.
Rys. 1. Minimalne drzewo rozpinające znalezione przez algorytm Kruskala
1.2. Własność przekroju
Załóżmy, że w procesie budowania minmalnego drzewa rozpinającego (MST) wybraliśmy już
pewne krawędzie. Którą krawędź powinniśmy teraz dodać? Poniższa własność daje nam dużą
elastyczność przy wyborze takiej krawędzi.
Własność przekroju. Przypuśćmy, że krawędzie zbioru X są częścią minimalnego drzewa rozpi-
nającego dla grafu
)
,
(
E
V
G
. Wybierz dowolny podzbiór wierzchołków S taki, że krawędzie z X
nie prowadzą z S do
S
V
i niech e będzie najlżejszą krawędzią między tymi dwoma zbiorami.
Wówczas
}
{e
X
jest częścią pewnego MST.
Przekrojem nazywamy dowolny podzial wierzchołków na dwie grupy, S oraz
S
V
. Po-
wyższa własność pokazuje, że zawsze „bezpiecznie” jest dodać najlżejszą krawędź przechodzącą
w poprzek przekroju (tzn. krawędź lączącą wierzchołek z S z wierzchołkiem z
S
V
), o ile X
nie zawiera krawędzi przechodzących w poprzek tego przekroju.
Uzasadnimy teraz, dlaczego zachodzi powyższa własność. Krawędzie zbioru X są częścią
pewnego minimalnego drzewa rozpinającego T: jeśli nowa krawędź również należy do drzewa T,
3
nie musimy niczego dowodzić. Przypuśćmy więc, że e nie należy do T. Przez nieznaczną zmianę
drzewa T, a mianowicie wymianę jego jednej krawędzi, skonstruujemy inne drzewo MST, T’,
zawierające
}
{e
X
.
Dodajmy krawędź e do T. Ponieważ T jest spójne, zawiera już ścieżkę między końcami
krawędzi e, czyli dodanie e powoduje powstanie cyklu. Cykl ten musi zawierać pewną krawędź
e’ przechodzącą w poprzek przekroju
)
,
(
S
V
S
(rys. 2). Jeśli teraz usuniemy tę krawędź, pozo-
stanie nam graf
}
'
{
}
{
'
e
e
T
T
, który jak dalej pokażemy, jest drzewem. Ponieważ e’ jest
krawędzią cyklu, własność 1 gwarantuje, że T’ jest spójne. Ma ono tyle samo krawędzi co drze-
wo T, czyli z własności 2 i 3 również jest drzewem.
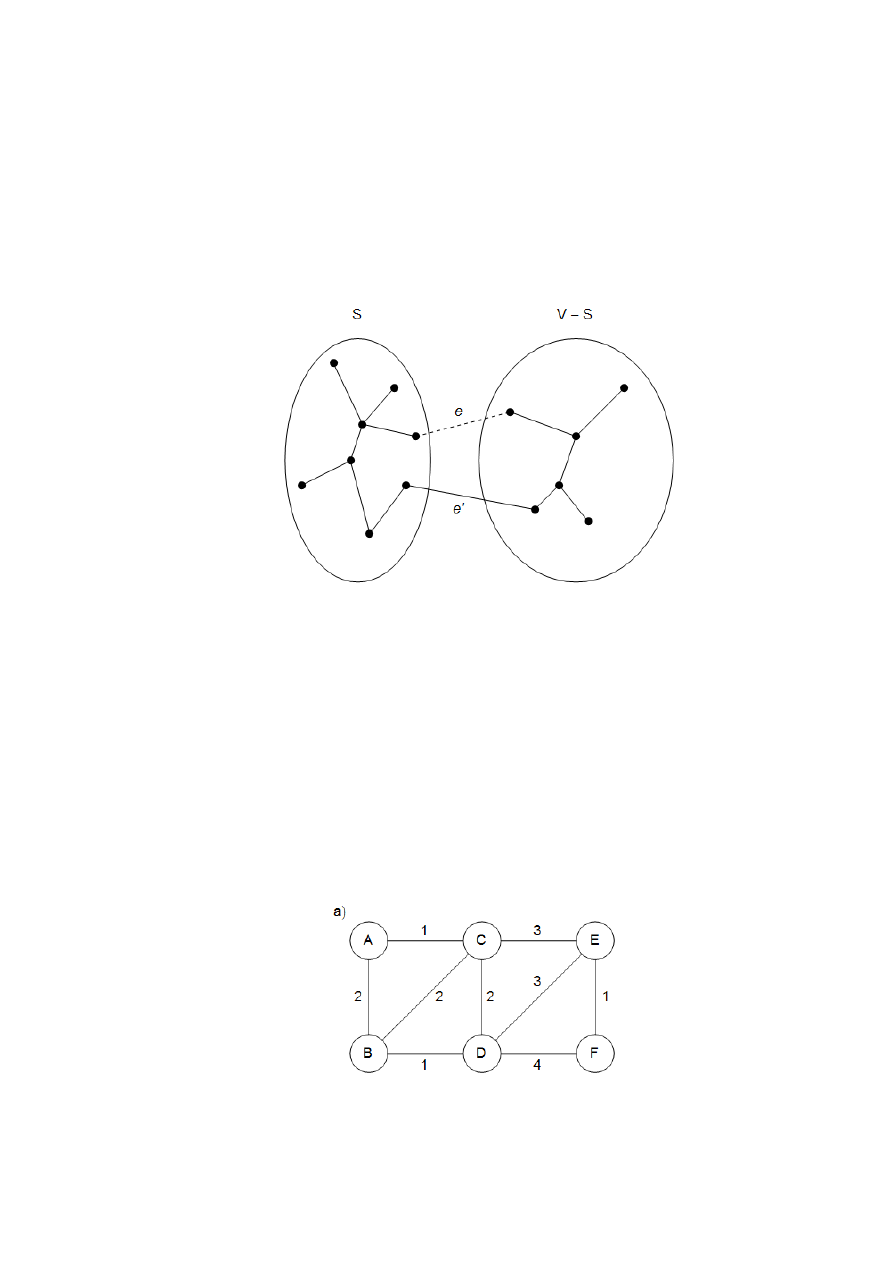
Rys. 2.
}
{e
T
. W wyniku dodania krawędzi e (linia przerywana) do drzewa T (linie ciągłe)
powstaje cykl. Cykl ten zawiera co najmniej jedną inną krawędź, nazwijmy ją e’, przechodzącą
w poprzek przekroju
)
,
(
S
V
S
Co więcej, T’ jest minimalnym drzewem rozpinającym. Obliczymy jego wagę w stosun-
ku do wagi T:
)
'
(
)
(
)
(
)
'
(
e
w
e
w
T
waga
T
waga
.
Obie krawędzie e oraz e’ prowadzą ze zbioru S do
S
V
oraz e jest najlżejszą krawędzią
tego typu. Oznacza to, że
)
'
(
)
(
e
w
e
w
oraz
)
(
)
'
(
T
waga
T
waga
. Ponieważ T jset minimalnym
drzewem rozpinającym, zachodzi równość
)
(
)
'
(
T
waga
T
waga
, co oznacza, że T’ również jest
drzewem MST.
Rys. 3 przedstawia przykład zastosowania własności przekroju.
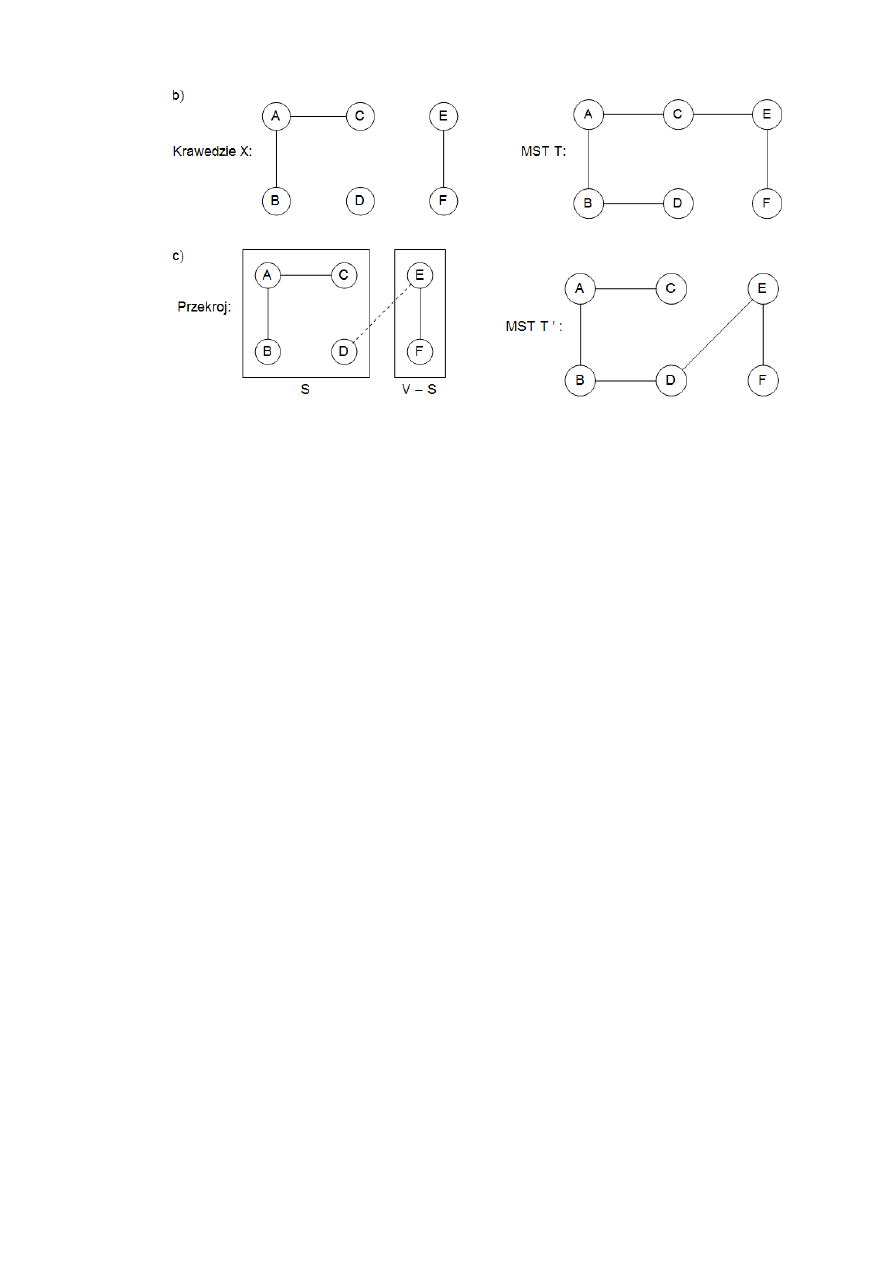
4
Rys. 3. Własność przekroju. a) Graf nieskierowany. b) Zbiór X: zawiera trzy krawędzi i jest czę-
ścią minimalnego drzewa rozpinającego T pokazanego po prawej. Jeśli
}
,
,
,
{
D
C
B
A
S
, to jedną
z krawędzi o minimalnej wadze przechdzącą w poprzek przekroju
)
,
(
S
V
S
jest
}
,
{
E
D
e
.
}
{e
X
jest częścią minimalnego drzewa rozpinającego T’, pokazanego po prawej
1.3. Algorytm Kruskala
Jesteśmy gotowi, aby uzasadnić poprawność algorytmu Kruskala. W każdym momencie wybra-
ne krawędzie tworzą częściowe rozwiązanie, zbiór spójnych składowych będących drzewami.
Kolejna dodana krawędź e lączy dwie składowe; nazwijmy je
1
T oraz
2
T . Ponieważ e jest naj-
lżejszą krawędzią, nietworzącą cyklu, mamy pewność, że jset to najlżejsza między
1
T oraz
1
T
V
spełniająca własność przekroju.
Uzupełnimy teraz szczegóły implementacyjne. Na każdym poziomie algorytm wybiera
krawędź i dodaje ją do aktualnego częściowego rozwiązania. W tym celu musi przetestować
każdą potencjalną krawędź
v
u
, sprawdzając, czy jej końce leżą w różnych składowych; w
przeciwnym razie w wyniku jej dodania powstanie cykl. Kiedy krawędź jest już wybrana, należy
połączyć odpowiednie składowe. Jaka struktura danych pozwali nam efektywnie wykonać takie
operacje?
Stany naszego algorytmu przedstawimy jako kolekcję zbiorów rozłącznych takich, że
każdy z nich zawiera wierzchołki jednej spójnej składowej. Początkowo każdy wierzchołek two-
rzy jedną składową:
)
(x
makeset
: utwórz nowy zbiór zawierający jeden element x.
Następnie wielokrotnie testujemy pary wierzchołków, aby sprawdzić, czy należą do tego samego
zbioru.
)
(x
find
: znajdź zbiór, do którego należy x (zwraca wskaźnik do reprezentanta zbioru)
Kiedy tylko dodajemy krawędź, łączymy dwie składowe.
)
,
(
y
x
union
: połącz zbiory zawierające x oraz y w nowy zbiór będąca ich sumą.
Uzyskany algorytm jest przedstawiony poniżej. Używa on
|
| V
operacji
makeset
,
|
|
2 E
operacji
find
oraz
1
|
|
V
operacji
union
.
5
Procedura kruskal(G, w)
Wejście: spójny graf nieskierowany
)
,
(
E
V
G
z wagami krawędzi
e
w ;
Wyjście: minimalne drzewo rozpinające zdefiniowane przez krawędzie zbioru X
for każdy wierzchołek
V
u
do
)
(u
makeset
od
X := { }
posortuj krawędzie E wg wag
for każda krawędź
E
v
u
}
,
{
w kolejności rosnących wag:
do if
)
(
)
(
v
find
u
find
then dodaj krawędź
}
,
{ v
u
do X;
)
,
( v
u
union
fi
od
1.4. Struktury danych dla zbiorów rozłącznych
1.4.1. Łączenie według rang. Jednym ze sposobów przechowywania zbioru jest zastosowanie
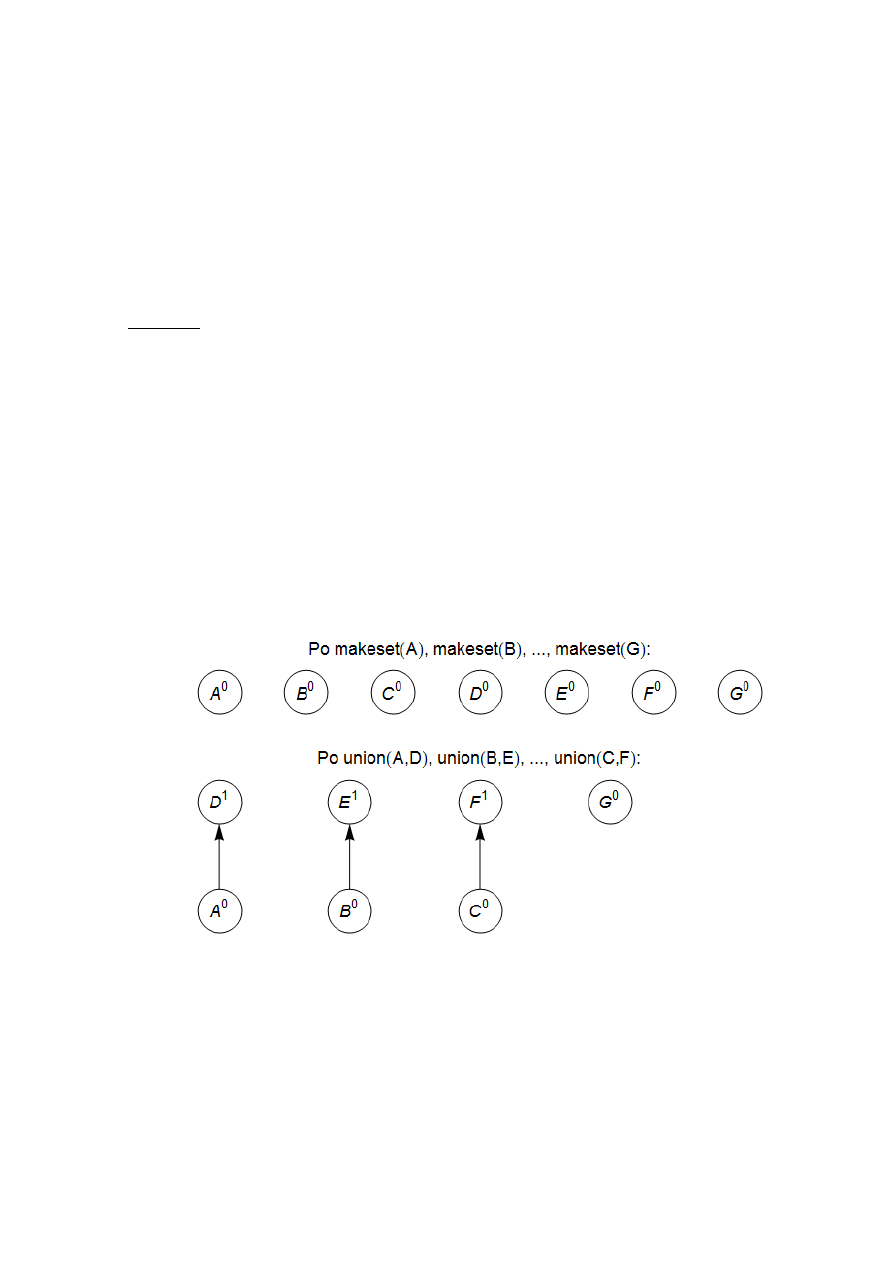
drzewa skierowanego (rys. 4). Węzłami drzewa są elementy zbioru rozmieszczone w drzewie w
dowolny sposób. Każdy węzeł ma wskaźnik na ojca. Wskaźniki te zmierzają w stronę korzenia
drzewa, który jest wygodnym reprezentantem (nazwą) zbioru. Korzeń wyróżnia się spośród in-
nych węzlów tym, że jego wskaźnik na ojca wskazuje na niego samego.
Rys. 4. Skierowane drzewo reprezentujące dwa zbiory
}
,
{
E
B
oraz
}
,
,
,
,
,
{
H
G
F
D
C
A
Dodatkowo, oprócz wskaźnika na ojca, każdy węzeł ma rangę, która może być interpre-
towana jako wysokość poddrzewa, którego korzeniem jest ten węzeł.
procedura
)
(x
makeset
x
x
:
)
(
0
:
)
(
x
rank
funkcja
)
(x
find
while
)
(x
x
do
)
(
:
x
x
od
return x
Zgodnie z oczekiwaniami operacja makeset działa w czasie stałym. Natomiast operacja find wę-
druje po wskaźnikach na ojców do korzenia, co zajmuje czas proporcjonalny do wysokości
6
drzewa. Budowanie drzewa odbywa sie za pomocą trzeciej operacji union, musimy więc zapew-
nić, by tworzyła ona drzewa niskie.
Lączenie dwóch drzew jest łatwe: wskaźnik korzenia jednego drzewa ustawiamy, tak aby
wskazywał na korzeń drugiego. Mamy w tym miejscu wybór. Jeśli reprezentantami (korzeniami)
zbiorów są
x
r oraz
y
r
, to lepiej jest ustawić
x
r , aby wskazywał na
y
r
, czy odwrotnie? Ponieważ
wysokość drzewa jest główną miarą efektywności algorytmu, dobrą strategią będzie ustawienie
korzenia niższego drzewa tak, aby wskazywał na korzeń wyższego. W ten sposób sumaryczna
wysokość drzewa zwiększy się tylko wtedy, gdy łączone drzewa są tak samo wysokie. Zamiast
dokładnie wyznaczać wysokości drzew, będziemy używać rang korzeni – dlatego właśnie po-
wyższy schemat postępowania jest nazywany łączeniem drzew według rang.
procedura
)
,
(
y
x
union
)
(x
find
r
x
)
( y
find
r
y
if
y
x
r
r
then return
if
)
(
)
(
y
x
r
rank
r
rank
then
x
y
r
r
:
)
(
else
y
x
r
r
:
)
(
if
)
(
)
(
y
x
r
rank
r
rank
then
1
)
(
)
(
y
y
r
rank
r
rank
fi
fi
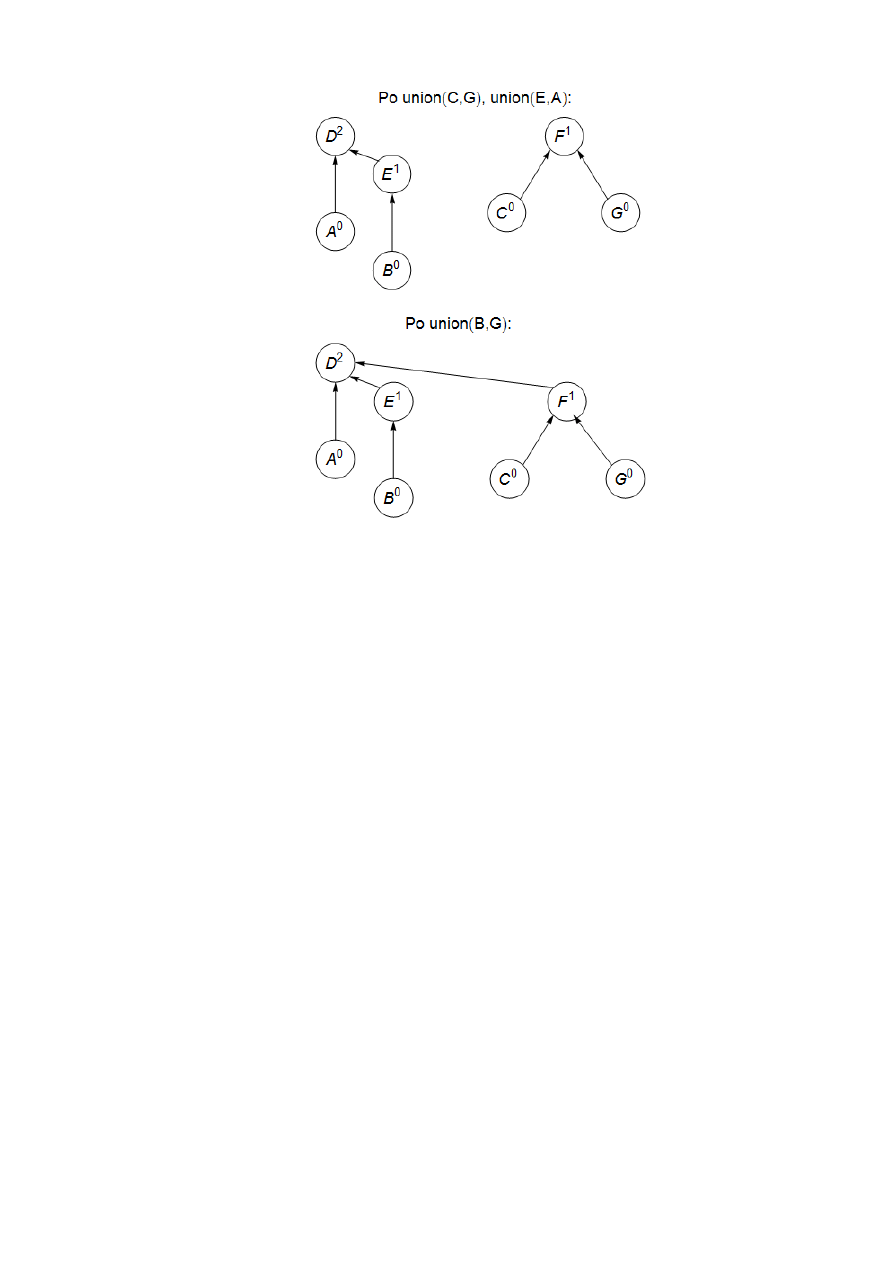
Zobacz przykład z rysunku 5.
7
Rys. 5. Sekwencja operacji na zbiorach rozłącznych. Indeksy górne oznaczają rangi
Zgodnie z opisanymi wyżej funkcjami wartość rank dla węzła oznacza dokładnie wyso-
kość poddrzewa, którego korzeniem jest dany węzel. Oznacza to, między innymi, że jeśli poru-
szamy się w gorę po drzewie w stronę korzenia, wartości rank wzdłuż tej ścieżki są ściśle rosną-
ce.
Własność 1. Dla każdego węzła x
))
(
(
)
(
x
rank
x
rank
.
Drzewo o korzeniu z ranga k powstaje przez połączenie dwóch drzew, których korzenie
mają rangi
1
k
. Obserwacja ta wraz z wykorzystaniem indukcji uzasadnia poniższą własność.
Własność 2. Jeśli korzeń drzewa ma rangę k , to drzewo to ma co najmniej
k
2 węzlów.
Własność tę można rozszerzyć na węzly wewnętrzne (nie będące korzeniami): węzeł o
randze k ma co najmniej
k
2 potomków. Każdy węzeł wewnętrzny był kiedyś korzeniem i od
tamtego czasu nie ulega zmianie ani jego ranga, ani zbiór potomków. Dodatkowo, dwa różne
węzły o randze k nie mają wspólnych potomków, ponieważ na mocy własności 1 każdy element
ma co najmniej jednego przodka o randze k. Otrzymujemy w ten sposób kolejną własność.
Własność 3. Jeśli w zbiorze jest łącznie n elementów, to węzłów o randze k jest co najwyżej
k
n 2
/
.
Ostatnia obserwacja implikuje, że maksymalną rangą w drzewie jest
n
log
. Innymi sło-
wy, wszystkie drzewa mają wysokość
n
log
i jest to ograniczenie górne na czas działania ope-
racji find oraz union.
1.4.2. Kompresja ścieżek. Łączny czas działania algorytmu Kruskala na strukturze danych
przedstawionej w tym rozdziale wynosi
|)
|
log
|
(|
V
E
O
dla posortowania krawędzi (przypomi-
namy, że
|
|
log
|
|
log
V
E
) i dodatkowe
|)
|
log
|
(|
V
E
O
dla operacji find oraz union, które do-
minują nad pozostałą częścią algorytmu. Wydaje się więc, że nie ma potrzeby szukać bardziej
efektywnej struktury danych.
8
Ale co w sytuacji, gdy krawędzie są dane jako posortowane? Albo gdy ich wagi są małe
(powiedzmy rzędu
|)
(| E
O
) i sortowanie nie może być wykonane w czasie liniowym? Wtedy
część algorytmu związana ze strukturą danych staje się wąskim gardłem i istotne jest pytanie,
czy jest możliwe poprawienie jej czasu działania tak, aby zejść poniżej czasu rzędu
n
log
na jed-
ną operację. Okazuje się, że taka efektywniejsza struktura jest i stała się użytecznym narzędziem
w wielu innych zastosowaniach.
W jaki sposób możemy wykonać operacje union i find, aby działały szybciej niż w czasie
rzędu
n
log
? Ogólna odpowiedź brzmi następująco: przez „większą ostrożność w zachowaniu
struktury w dobrym kształcie”. Każda osoba utrzymująca porządek wie, że mały dodatkowy wy-
siłek włożony w rutynowe czynności zwraca się przez długi czas i zapobiega większym katastro-
fom. Mamy tu na myśli wykonywanie konkretnej dodatkowej pracy w naszej strukturze find-
union zmierzającej do uzyskiwania niższych drzew – podczas każdej operacji find, kiedy prze-
glądamy kolejne wskaźniki do ojców, wędrując w stronę korzenia drzewa, będziemy zmieniać te
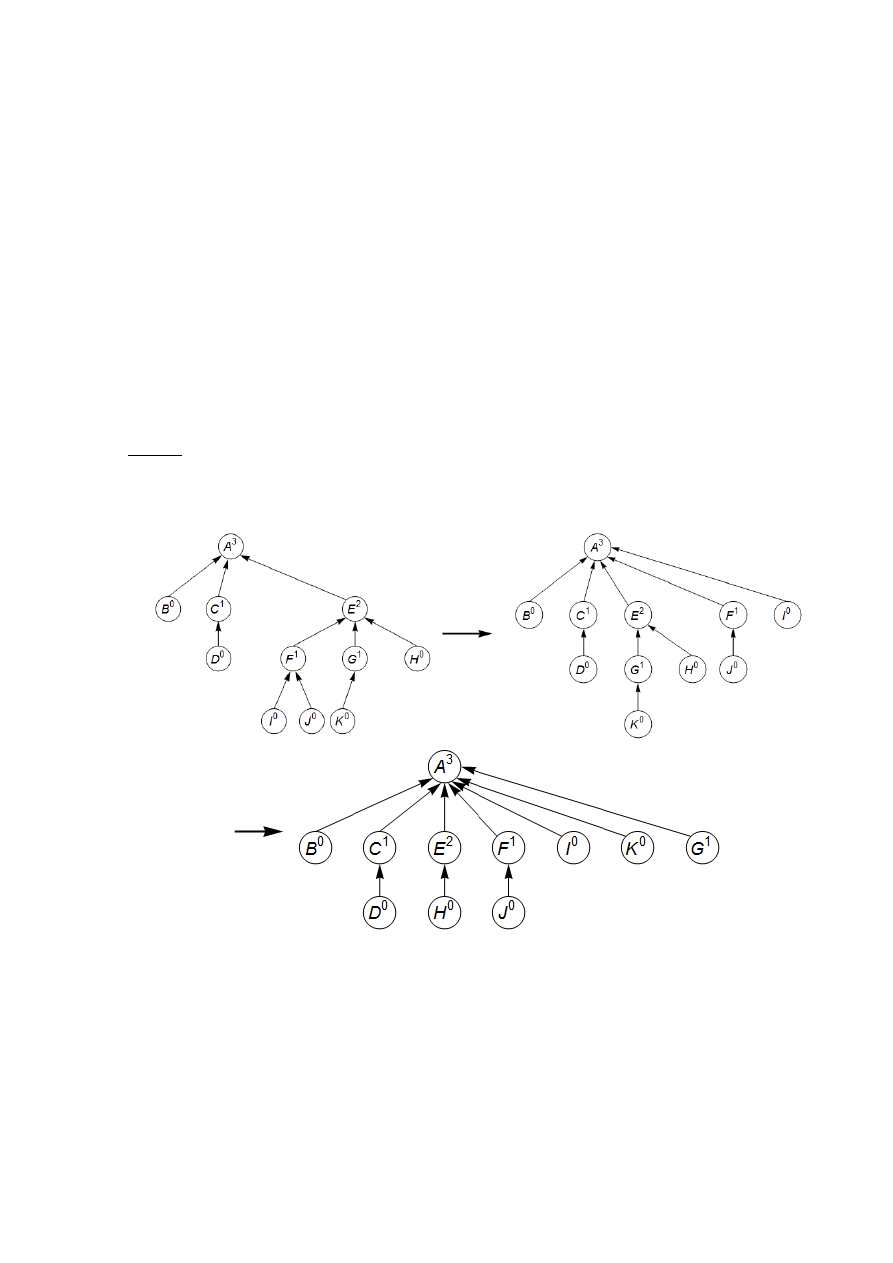
wskaźniki tak, aby wszystkie węzły na ścieżce wskazywały na korzeń drzewa (rys. 6). Taka
kompresja ścieżek tylko nieznacznie zwiększa czas potrzebny operacji find i jest łatwa do zako-
dowania.
funkcja
)
(x
find
while
)
(x
x
do
))
(
(
:
)
(
x
find
x
od
return x
Rys. 6. Wynik kompresji ścieżek: po operacji find(I) oraz find(K)
Kożyść tej prostej poprawki jest raczej długoterminowa niż natychmiastowa, dlatego też
wymaga specjalnej analizy: będziemy rozważać ciąg operacji find oraz union, zaczynając od pu-
stej struktury, i oszacujemy średni czas przypadający na jedną operacje. Taki koszt zamortyzo-
wany okaże się być niewiele większy niż
)
1
(
O
i mniejszy niż wcześniejsze
)
(log n
O
.
Wyobraźmy sobie, że nasza struktura danych składa się z „górnego poziomu” zawierają-
cego korzenie drzew oraz niższego poziomu zawierającego wnętrza drzew. Podział pracy jest
następujący: operacje find (z kompresją ścieżki lub nie) analizują jedynie wnętrza drzew, pod-
czas gdy operacje union – tylko poziom górny. Kompresja ścieżek nie ma więc żadnego znacze-
nia dla operacji union i pozostawia górny poziom niezmieniony.
9
Wiemy już, że rangi korzeni pozostają niezmienione, a co z rangami pozostałych wę-
złów? Kluczową obserwacją jest, że jeśli węzeł przestaje być korzeniem, już nigdy nie „wypły-
nie na powierzchnie” i jego ranga jest ustalona na stałe. Czyli kompresja ścieżek nie zmienia
rang wszystkich węzłów, chociaż liczby te nie mogą być interpretowane jako wysokości drzew.
W szczególności, własności 1-3 (r. 1.4.1) pozostają prawdziwe.
Własność 3 mówi, że jeśli mamy n elementów, ich rangi są wartościami z przedziału od 0
do
n
log
. Podzielmy niezerowe wartości tego przedziału na ostrożnie wybrane przedziały (zasa-
da tego podziału stanie się niedługo zrozumiała):
}
1
{
,
}
2
{
,
}
4
,
3
{
,
}
16
,...,
6
,
5
{
,
}
65536
2
,...,
18
,
17
(
16
,
}
2
,...,
65538
,
65537
(
65536
, ...
Każda grupa jest postaci
}
2
,...,
2
,
1
{
k
k
k
, gdzie k jest potęgą liczby 2. Liczba grup
wynosi
n
log*
. Wartość ta zdefiniowana jest jako liczba kolejnych operacji wykonania logaryt-
mu dwójkowego potrzebnych, aby rozpoczynając od liczby n, zejść do 1 (lub poniżej 1). Dla
przykładu,
4
1000
log*
, ponieważ
1
1000
log
log
log
log
. W praktyce używanych jest jedunie
pierwszych 5 przedziałów, pozostale byłyby potrzebne, gdyby
65536
2
n
, czyli nigdy.
W sekwencji operacji find niektóre z nich mogą działać dłużej od pozostałych. Ogra-
niczmy łączny czas działania sekwencji, używając pomysłowego sposobu liczenia. Każdemu
węzłowi drzewa przypiszemy pewną liczbę monet 1-złotowych, tak aby łączna liczba przydzie-
lonych monet wynosiła co najwyżej
n
n log*
. Pokażemy teraz, że każda operacja find zajmuje
)
(log* n
O
kroków plus pewną dodatkową ilość czsu, jaka może być zapłacona przy użyciu
wcześniej przypisanych monet – jedna moneta za jedną jednostkę czasu. Łączny czas m operacji
find będzie wynosił
)
log*
(
n
m
O
plus co najwyżej
)
log*
(
n
n
O
.
Każdy węzeł otrzymuje swoją należność, gdy przestaje być korzeniem. W tym momien-
cie jego ranga jest już ustalona. Jeśli ranga leży w przedziale
}
2
,...,
2
,
1
{
k
k
k
, węzeł otrzymu-
je
k
2 złotych. Z własności 3 mamy, że liczba węzłów z rangą większą niż k jest organiczona
przez
k
k
k
n
n
n
2
...
2
2
2
1
.
Czyli całkowita liczba monet danych węzłów w tym szczególnym przedziale jest ograniczona
przez n. Ponieważ przedziałów jest co najwyżej
n
log* , łącznie wszystkich wydanych monet jest
co najwyżej
n
n log*
.
Czas potrzebny konkretnej operacji find jest równy liczbie węzłów, które ona analizuje.
Rozważmy rosnący ciąg wartości rang wzdłuż lańcucha węzłów prowadzących do korzenia.
Węzły te dzielą się na dwie kategorie: albo ranga
)
(x
należy do wyższego przedziłu niż ranga
x, albo obie rangi leżą w tym samym przedziale. Jest to najwyżej
n
log* węzłów pierwszego ro-
dzaju, czyli praca na nich wykonana zabierze
)
(log* n
O
czasu. Pozostałe węzły – czyli te, dla
których ich ranga oraz ranga rodzica leżą w tym samym przedziałe – płacą jedna monetę za czas
ich analizy.
Zasada płacenia monetami za czas będzie działała dobrze, jeśli początkowa liczba monet
jest wystarczjąca do pokrycia ich zapotrzebowania przez sekwencję operacji find. Poniższa ob-
serwacja jest najistotniejsza dla zrozumienia poprawności całego rozumowania: za każdym ra-
zem, kiedy węzeł płaci jedną monetę, jego rodzicem staje się węzeł o wyższej randze. Czyli, jeśli
ranga należy do przedziału
}
2
,...,
2
,
1
{
k
k
k
, musi on zapłacić co najwyżej
k
2 monet., zanim
ranga jego rodzica wskoczy do wyższego przedziału i wówczas nie będzie już musiał więcej pła-
cić.
10
1.5. Algorytm Prima
Powróćmy do naszych rozważań o algorytmach znajdowania minimalnego drzewa rozpinające-
go. Własność przekroju gwarantuje, że każdy algorytm zbudowany według poniższego schematu
będzie działał poprawnie.
X = {} // krawędzie wybrane do tej pory
repeat until
1
|
|
V
X
do
wybierz zbiór
V
S
taki, że w X nie ma krawędzi między S oraz
S
V
niech
E
e
będzie krawędź między S oraz
S
V
o najmniejszej wadze
}
{e
X
X
od
Popularnaą alternatywą dla algorytmu Kruskala jest algorytm Prima, w którym pośrednie
zbiory krawędzi X zawsze tworzą poddrzewo, a S jest zbiorem węzłów tego drzewa.
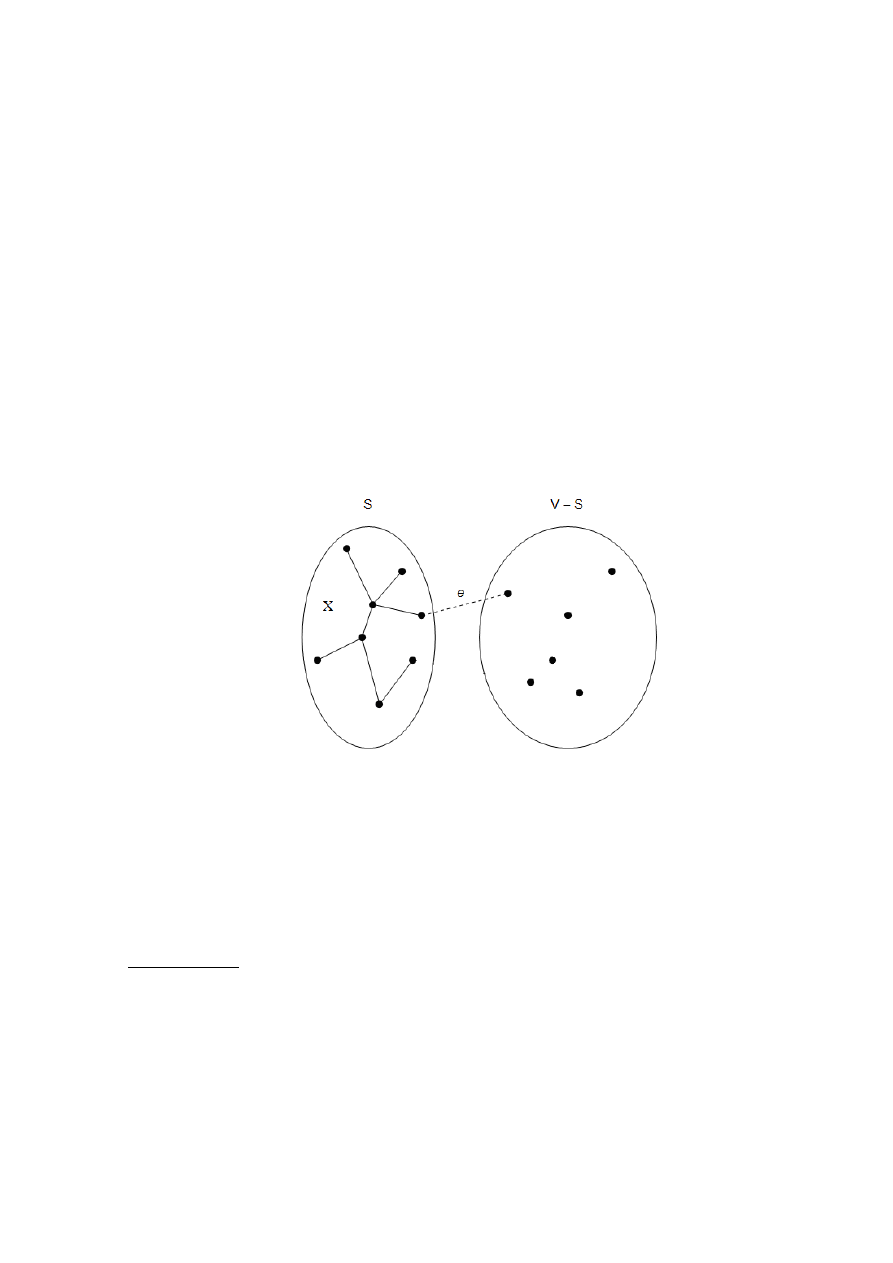
Każda iteracja rozszerza poddrzewo zdefiniowane przez X o jedną krawędź, mianowicie
tę krawędź, która była najlżejsza spośród krawędzi łączących wierzchołki z S z tymi poza S (rys.
7). Równoważnie możemy powiedzieć, że rozszerzamy S przez dodanie wierzchołka
S
v
o
najmniejszej wartości cost:
)
,
(
min
)
(
cos
v
u
w
v
t
S
u
.
Rys. 7. Algorytm Prima: krawędzie zbioru X tworzą drzewo, S składa się z jego węzłów
Działanie algorytmu bardzo przypomina algorytm Dijkstry i w rzeczywistości pseudoko-
dy obu tych algorytmów są prawie identyczne. Jedyna różnica jest sposób uporządkowania ko-
lejki priorytetowej. W algorytmie Prima wartością wierzchołka jest waga najlżejszej krawędzi
wychodzącej ze zbioru S, podczas gdy w algorytmie Dijkstry jest nią długość ścieżki prowadzą-
cej z punktu startowego do tego wierzchołka. Niezależnie od tej różnicy oba algorytmy mają taki
sam czas działania, zależny od implementacji kolejki priorytetowej.
Procedura prim(G, w)
Wejście: spójny nieskierowany graf
)
,
(
E
V
G
z wagami krawędzi
e
w ;
Wyjście: minimalne drzewo rozpinające zdefiniowane przez tablicę prev
for każdy wierzchołek
V
u
do
:
)
(
cos u
t
nil
u
prev
:
)
(
od
0
:
)
(
cos
0
u
t
// wybierz dowolny początkowy wierzchołek
0
u
H := makequeue(V) // kolejka priorytetowa, której kluczami są wartości cost
while
H
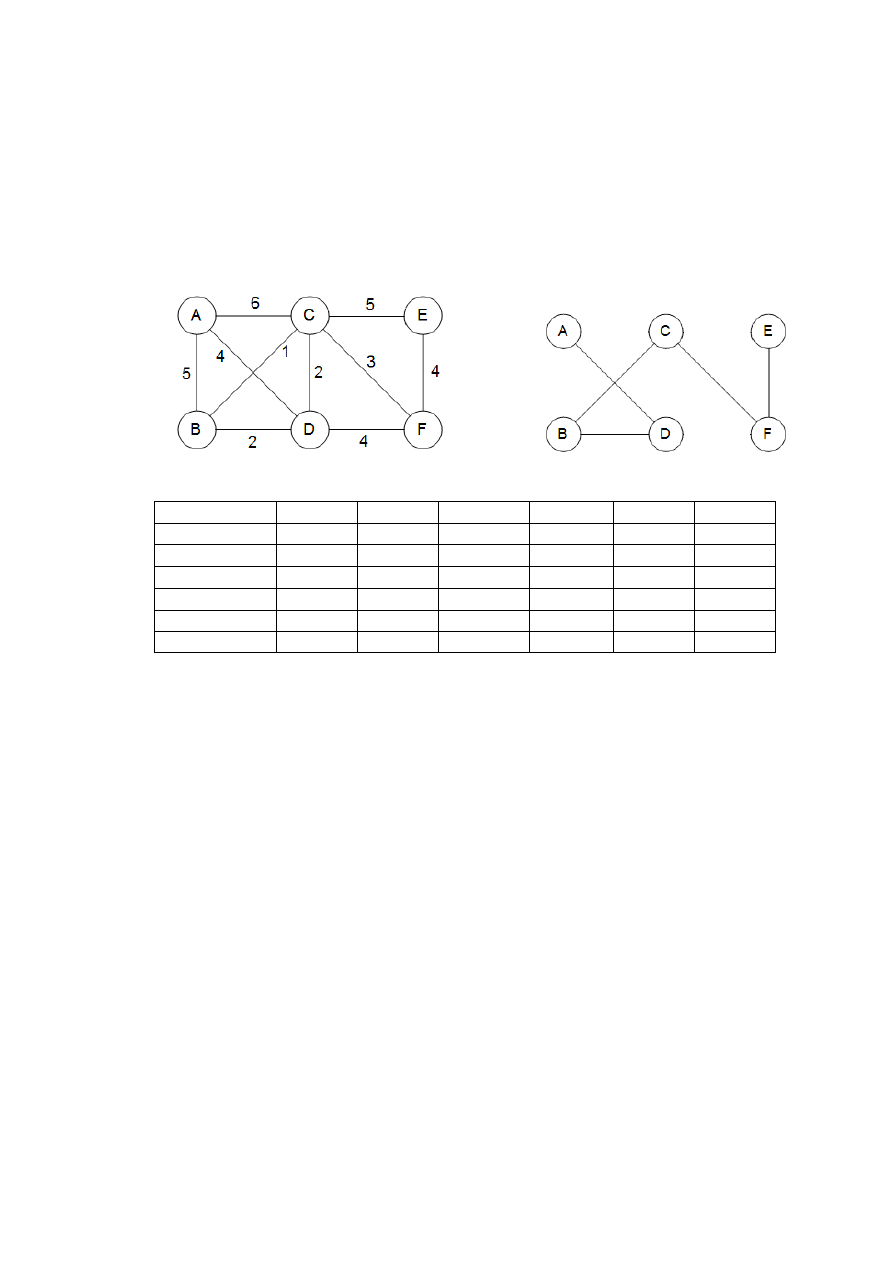
11
do
:
u
deletemin(H)
for każda krawędź
E
z
u
)
,
(
do if
H
z
and
)
,
(
)
(
cos
z
u
w
z
t
then
)
,
(
)
(
cos
z
u
w
z
t
;
u
z
prev
)
(
; fi
od
od
Rys. 8. Działanie algorytmu Prima znajdowania minimalnego drzewa rozpinającego
Zbiór S
A
B
C
D
E
F
{}
0/nil
nil
/
nil
/
nil
/
nil
/
nil
/
A
5/A
6/A
4/A
nil
/
nil
/
A,D
2/D
2/D
nil
/
4/D
A,D,B
1/B
nil
/
4/D
A,D,B,C
5/C
3/C
A,D,B,C,F
4/F