Podstawy elektroenergetyki rok II, semestr III

Podstawy elektroenergetyki rok II, semestr III

Energetyka

Energetyka

Konwencjonalna

Konwencjonalna

wykład nr 2

wykład nr 2

Plan Prezentacji

Plan Prezentacji

1. Właściwości czynnika roboczego (wody i pary

1. Właściwości czynnika roboczego (wody i pary

wodnej)

wodnej)

5. Obieg Rankine’a i teoretyczna sprawność tego

5. Obieg Rankine’a i teoretyczna sprawność tego

obiegu

obiegu

2. Wykresy

2. Wykresy

T - s

T - s

oraz

oraz

i – s

i – s

dla wody i pary wodnej

dla wody i pary wodnej

3. Przemiany energetyczne

3. Przemiany energetyczne

4. Teoretyczne obiegi cieplne

4. Teoretyczne obiegi cieplne

6. Sprawność elektrowni brutto i netto

6. Sprawność elektrowni brutto i netto

Równania klasycznej termodynamiki, znane jako prawa Boyle'a-Mariotte'a, Gay-Lussaca, Avogadro i Joule'a-Thompsona są słuszne dla tzw. gazów doskonałych.

Równania klasycznej termodynamiki, znane jako prawa Boyle'a-Mariotte'a, Gay-Lussaca, Avogadro i Joule'a-Thompsona są słuszne dla tzw. gazów doskonałych.

Do obliczeń praktycznych i potrzeb kontroli pracy elektrowni parowych stosuje się powszechnie wartości parametrów zestawione w tablicach pary wodnej. Właściwości te są określane prze następujące

Do obliczeń praktycznych i potrzeb kontroli pracy elektrowni parowych stosuje się powszechnie wartości parametrów zestawione w tablicach pary wodnej. Właściwości te są określane prze następujące

parametry ciśnienie

parametry ciśnienie

p

p

, temperaturę

, temperaturę

t

t

, objętość

, objętość

v,

v,

entalpie

entalpie

i

i

oraz entropię

oraz entropię

s

s

.

.

Definicje entalpii oraz entropii:

Definicje entalpii oraz entropii:



Entalpia właściwa jest ilością ciepła niezbędna do doprowadzenia

Entalpia właściwa jest ilością ciepła niezbędna do doprowadzenia

1 kg

1 kg

czynnika od umownego punktu początkowego do pewnego punktu końcowego

czynnika od umownego punktu początkowego do pewnego punktu końcowego

przy

przy

p=const.

p=const.

Wartość liczbowa entalpii zależy od stanu czynnika, oraz para-

Wartość liczbowa entalpii zależy od stanu czynnika, oraz para-

metrów wyznaczających ten stan.

metrów wyznaczających ten stan.



Entropia nie ma interpretacji fizycznej, wprowadzenie jej jako pojęcia o

Entropia nie ma interpretacji fizycznej, wprowadzenie jej jako pojęcia o

charakterze matematycznym pozwala na przedstawienie obiegów termo-

charakterze matematycznym pozwala na przedstawienie obiegów termo-

dynamicznych za pomocą przejrzystych i wygodnych w użytkowaniu wykresów.

dynamicznych za pomocą przejrzystych i wygodnych w użytkowaniu wykresów.

Entropia jest wielkością zależną od stanu czynnika. Jest jednym z parametrów

Entropia jest wielkością zależną od stanu czynnika. Jest jednym z parametrów

określających zdolność zamiany ciepła w energię mechaniczną.

określających zdolność zamiany ciepła w energię mechaniczną.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

3

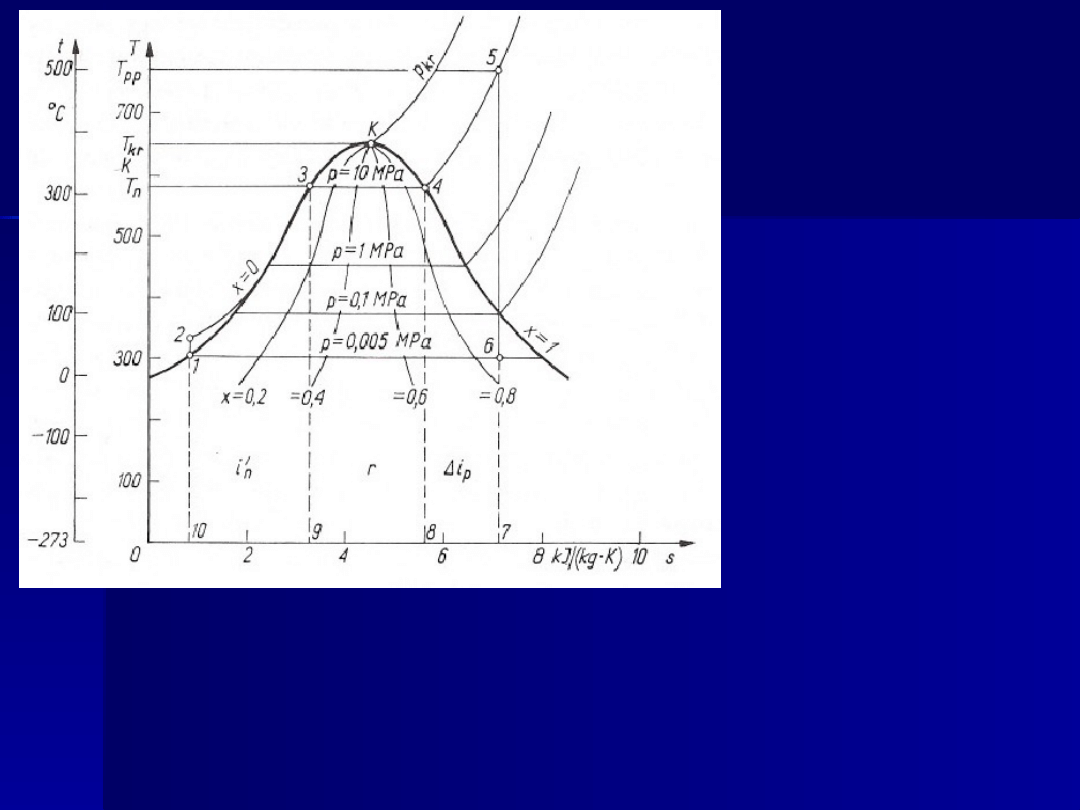
Rys. 1. Wykres

Rys. 1. Wykres

T-s

T-s

dla wody i pary wodnej

dla wody i pary wodnej

Na wykresie

Na wykresie

T-s

T-s

, pole

, pole

1-2-3-9-10-1

1-2-3-9-10-1

przedstawia entalpie i wody w stanie

przedstawia entalpie i wody w stanie

nasycenia (wrzenia), pole

nasycenia (wrzenia), pole

3-4-8-9-3

3-4-8-9-3

ciepło parowania

ciepło parowania

r

r

, a pole

, a pole

4-5-7-8-4

4-5-7-8-4

-

-

ciepło przegrzania

ciepło przegrzania





i

i

p

p

pary nasyconej suchej od

pary nasyconej suchej od

T

T

n

n

do

do

T

T

pp

pp

. Suma tych trzech

. Suma tych trzech

pól, czyli całkowite pole

pól, czyli całkowite pole

10-1-2-3-4-5-7-10

10-1-2-3-4-5-7-10

, przedstawia entalpie pary

, przedstawia entalpie pary

przegrzanej.

przegrzanej.

Parametry krytyczne

Parametry krytyczne

pary wodnej dla cieczy

pary wodnej dla cieczy

i pary suchej są takie

i pary suchej są takie

same:

same:

P

P

kr

kr

=22,13 MPa,

=22,13 MPa,

T

T

kr

kr

=374,15°C,

=374,15°C,

V

V

kr

kr

=0,00315 m3/kg,

=0,00315 m3/kg,

i

i

kr

kr

= 2095,2 kJ/kg,

= 2095,2 kJ/kg,

S

S

kr

kr

= 4,424 kJ/(kg

= 4,424 kJ/(kg





K),

K),

ciepło parowania r = 0.

ciepło parowania r = 0.

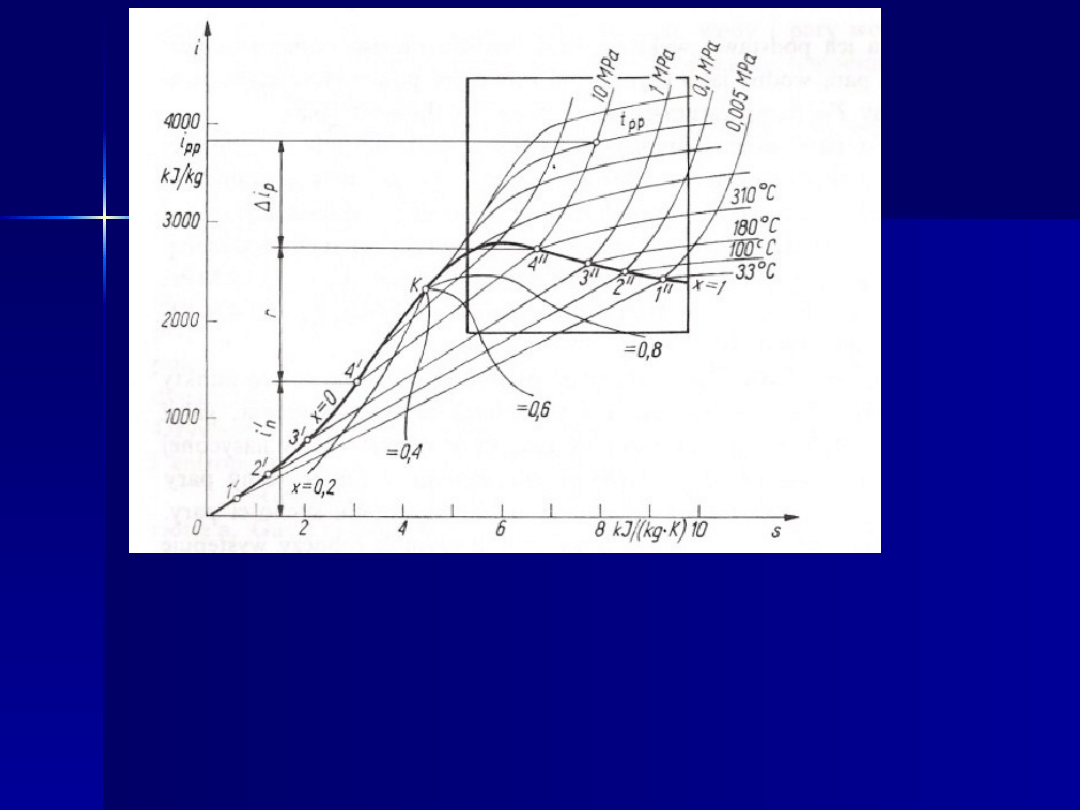
Rys. 2. Wykres

Rys. 2. Wykres

i-s

i-s

dla wody i pary wodnej opracowany przez R. Molliera

dla wody i pary wodnej opracowany przez R. Molliera

Zaleta wykresu

Zaleta wykresu

i-s

i-s

polega na tym, ze łatwa do odczytania na wykresie

polega na tym, ze łatwa do odczytania na wykresie

różnica rzędnych dwóch punktów, odpowiadających różnym parametrom

różnica rzędnych dwóch punktów, odpowiadających różnym parametrom

czynnika roboczego, czyli różnica entalpii czynnika jest ilością ciepła jaką

czynnika roboczego, czyli różnica entalpii czynnika jest ilością ciepła jaką

1

1

kg

kg

masy czynnika wymienił z otoczeniem. Znaczne różnice w gradientach

masy czynnika wymienił z otoczeniem. Znaczne różnice w gradientach

parametrów dla różnych stanów skupienia powodują, ze drukowanie

parametrów dla różnych stanów skupienia powodują, ze drukowanie

pełnych wykresów (od

pełnych wykresów (od

i = 0

i = 0

oraz

oraz

s = 0

s = 0

) jest niecelowe.

) jest niecelowe.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

6

v

p

u

i







w

w

w

t

c

i





x

r

t

c

i

n

w

x









)

(

'

"

n

pp

pp

pp

pp

t

t

c

r

i

i

i

i















'

"

'

V

V

V

V

x

x







Podstawowe

Podstawowe

wzory

wzory

do

obliczeń

do

obliczeń

cieplnych

cieplnych

Entalpia wody:

Entalpia wody:

Entalpia pary mokrej:

Entalpia pary mokrej:

Entalpia pary przegrzanej:

Entalpia pary przegrzanej:

Stopień suchości pary:

Stopień suchości pary:

Entalpia (wzór ogólny):

Entalpia (wzór ogólny):

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

7

Rod

Rod

z

z

aje

przemian

aje

przemian

energetycznych

energetycznych

Przemiana izotermiczna

Przemiana izotermiczna

– zachodzi przy stałej

– zachodzi przy stałej

temperaturze, w obszarze pary mokrej jest

temperaturze, w obszarze pary mokrej jest

jednocześnie przemianą izobaryczną. Ciepło dostar-

jednocześnie przemianą izobaryczną. Ciepło dostar-

czane parze jest zużywane na zwiększenie energii

czane parze jest zużywane na zwiększenie energii

wewnętrznej oraz wykonanie pracy zewnętrznej.

wewnętrznej oraz wykonanie pracy zewnętrznej.

1

2

1

2

12

)

(

i

i

x

x

r

q













Przy rozprężaniu izotermicznym pary mokrej, rośnie

Przy rozprężaniu izotermicznym pary mokrej, rośnie

stopień jej su-chości. Para nasycona sucha przy

stopień jej su-chości. Para nasycona sucha przy

rozprężaniu izotermicznym prze-chodzi w parę mokrą,

rozprężaniu izotermicznym prze-chodzi w parę mokrą,

a przy sprężaniu w

a przy sprężaniu w

parę przegrzaną

parę przegrzaną

.

.

Przemiana izobaryczna

Przemiana izobaryczna

– występuje przy stałym

– występuje przy stałym

ciśnieniu, ciepło dostar-czane do czynnika powoduje

ciśnieniu, ciepło dostar-czane do czynnika powoduje

wzrost entalpii czynnika.

wzrost entalpii czynnika.

Cześć dostarczanego ciepła powoduje podniesienie

Cześć dostarczanego ciepła powoduje podniesienie

energii wewnę-trznej, a część wykonanie pracy

energii wewnę-trznej, a część wykonanie pracy

przetłaczania.

przetłaczania.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

8

Rod

Rod

z

z

aje przemian energetycznych

aje przemian energetycznych

cd.

cd.

)

(

1

2

v

v

p

u

q











Podczas tej przemiany w obszarze pary mokrej

Podczas tej przemiany w obszarze pary mokrej

temperatura zostaje stała a rośnie suchość pary. W

temperatura zostaje stała a rośnie suchość pary. W

obszarze pary przegrzanej szybko rośnie tempe-ratura.

obszarze pary przegrzanej szybko rośnie tempe-ratura.

Rod

Rod

z

z

aje przemian energetycznych

aje przemian energetycznych

cd.

cd.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

9

Przemiana izochoryczna

Przemiana izochoryczna

– przy stałej objętości, praca

– przy stałej objętości, praca

zewnętrzna równa zero, ciepło doprowadzane jest

zewnętrzna równa zero, ciepło doprowadzane jest

zużywane na przyrost energii wewnętrznej.

zużywane na przyrost energii wewnętrznej.

1

2

u

u

q







Przy dostarczaniu ciepła parze wodnej przy

Przy dostarczaniu ciepła parze wodnej przy

V = const

V = const

.

.

rośnie jej

rośnie jej

t, p, i

t, p, i

,

,

w obszarze pary mokrej rośnie

w obszarze pary mokrej rośnie

x

x

, przy odbieraniu ciepła

, przy odbieraniu ciepła

proces zachodzi

proces zachodzi

w drugą stronę.

w drugą stronę.

Przemiana izentalpowa

Przemiana izentalpowa

– dławienie para przeciskają

– dławienie para przeciskają

się przez szczelnie traci ciśnienie,

się przez szczelnie traci ciśnienie,

i = const

i = const

.,

.,

wzrasta

wzrasta

V

V

maleje nieznacznie

maleje nieznacznie

t

t

. Silne dławienie pary

. Silne dławienie pary

mokrej może spowodować przegrzanie pary.

mokrej może spowodować przegrzanie pary.

Rod

Rod

z

z

aje przemian energetycznych

aje przemian energetycznych

cd.

cd.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

10

Przemiana adiabatyczna

Przemiana adiabatyczna

– charakteryzuje się brakiem

– charakteryzuje się brakiem

wymiany ciepła między czynnikiem z otoczeniem.

wymiany ciepła między czynnikiem z otoczeniem.

Praca zewnętrzna podczas tej przemiany powstaje

Praca zewnętrzna podczas tej przemiany powstaje

kosztem

energii

wewnętrznej

czynnika.

Przy

kosztem

energii

wewnętrznej

czynnika.

Przy

rozprężaniu

adiabatycznym

pary,

obniża

się

rozprężaniu

adiabatycznym

pary,

obniża

się

temperatura, maleje stopień suchości ( punkt

temperatura, maleje stopień suchości ( punkt

końcowy obszar pary mokrej ) oraz zwiększa się

końcowy obszar pary mokrej ) oraz zwiększa się

objętość pary.

objętość pary.

Przemiana politropowa

Przemiana politropowa

– występuje w rzeczywistych

– występuje w rzeczywistych

silnikach cieplnych, praca wykonywana przez czynnik

silnikach cieplnych, praca wykonywana przez czynnik

wiąże się ze stratami polegającymi na wymianie ciepła

wiąże się ze stratami polegającymi na wymianie ciepła

z otoczeniem, tarciem cząstek pary o ścianki przy-

z otoczeniem, tarciem cząstek pary o ścianki przy-

rządów rozprężających oraz o siebie.

rządów rozprężających oraz o siebie.

Przy rozprężaniu pary na skutek strat mniejszy

Przy rozprężaniu pary na skutek strat mniejszy

spadek entalpii zamieniany jest na pracę w

spadek entalpii zamieniany jest na pracę w

porównaniu z rozprężaniem adiabatycznym.

porównaniu z rozprężaniem adiabatycznym.

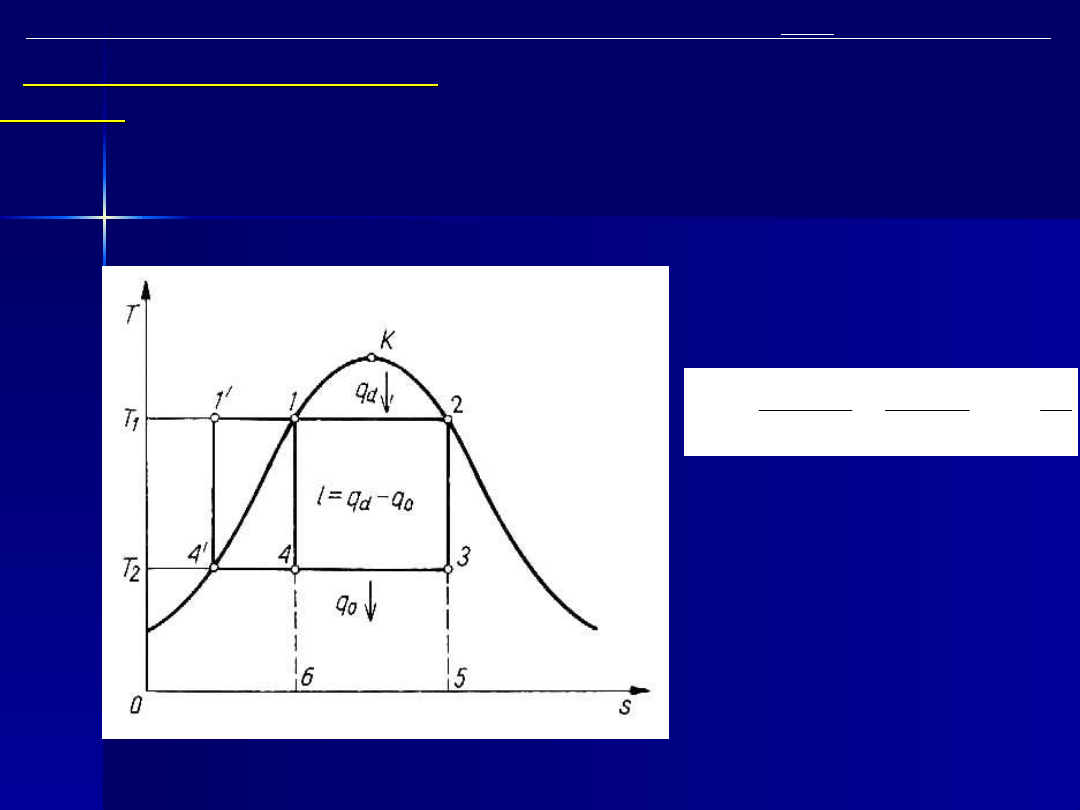
Teoretyczny

obieg

Teoretyczny

obieg

Carnota

Carnota

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

11

Obiegi stosowane w elektrowniach parowych opierają się na

Obiegi stosowane w elektrowniach parowych opierają się na

teoretycznym obiegu Carnota, który zapewnia największą

teoretycznym obiegu Carnota, który zapewnia największą

sprawność przemiany energii cieplnej w mechaniczną dla

sprawność przemiany energii cieplnej w mechaniczną dla

określonych temperatur górnego i dolnego źródła ciepła.

określonych temperatur górnego i dolnego źródła ciepła.

Rys. 3. Obieg Carnota dla pary nasyconej

Sprawność teoretyczna obiegu
Carnota:

1

2

1

2

1

1

T

T

T

T

T

q

q

q

d

o

d

tC















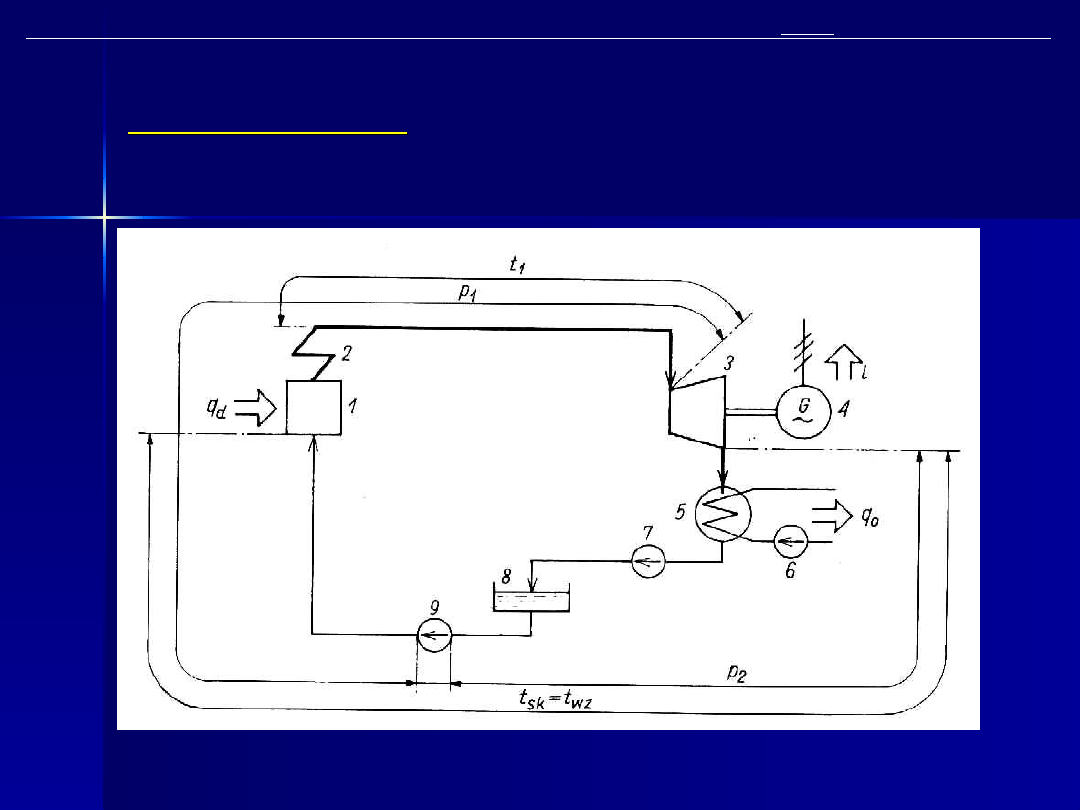
Obieg Rankine’a

Obieg Rankine’a

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

12

Rys. 4. Ideowy schemat obiegu cieplnego elektrowni parowej kondensacyjnej

Graficzne przedstawienie przemian

Graficzne przedstawienie przemian

energetycznych zachodzących

energetycznych zachodzących

w obiegu Rankine’a

w obiegu Rankine’a

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

13

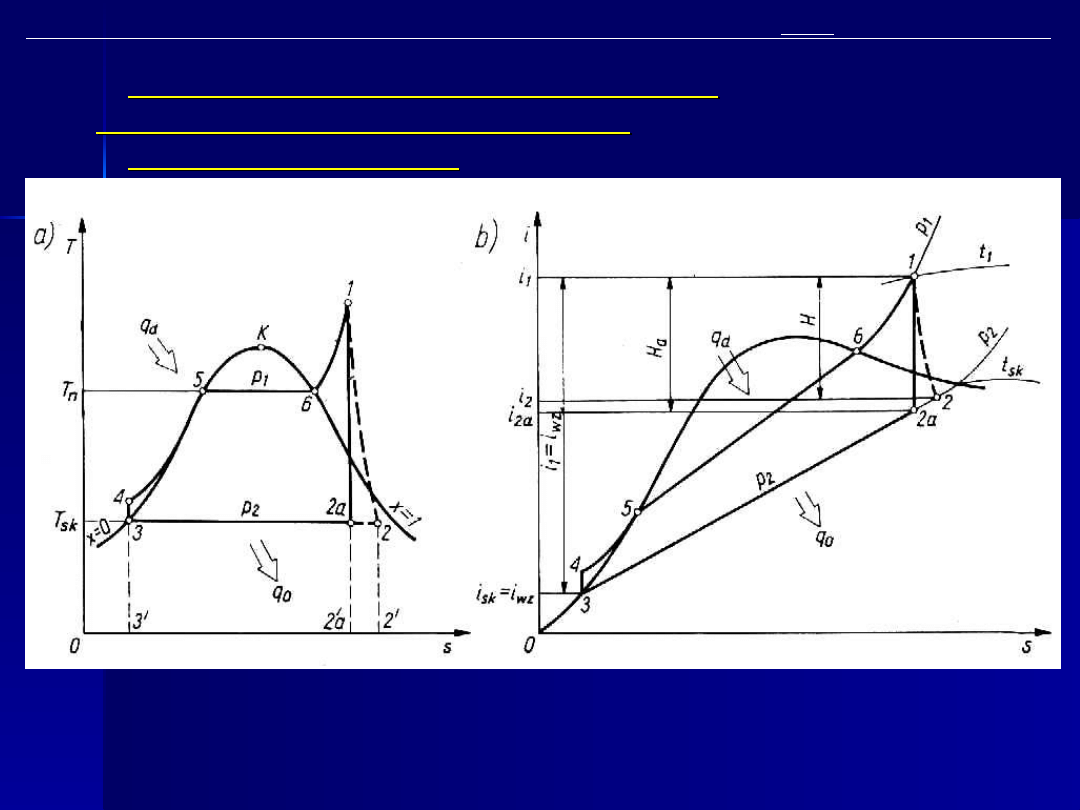
Rys. 5. Obieg Rankine’a elektrowni parowej kondensacyjnej:

a) w układzie T-s; b) w układzie i-s

Wyprowadzenie wzoru na teoretyczną sprawność

Wyprowadzenie wzoru na teoretyczną sprawność

obiegu Rankine’a

obiegu Rankine’a

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

14

Przy założeniu, że w obiegu krąży masa 1 kg czynnika roboczego,
ciepło doprowadzone do obiegu można określić:

wz

d

i

i

q





1

Natomiast ciepło nie wykorzystane, oddane z obiegu w skraplaczu można określić:

sk

a

o

i

i

q





2

Sprawność teoretyczna obiegu Rankine’a:

wz

sk

wz

a

wz

sk

a

wz

d

o

d

t

i

i

i

i

i

i

i

i

i

i

i

i

q

q

q

























1

2

1

1

2

1

)

(

)

(

)

(

)

(



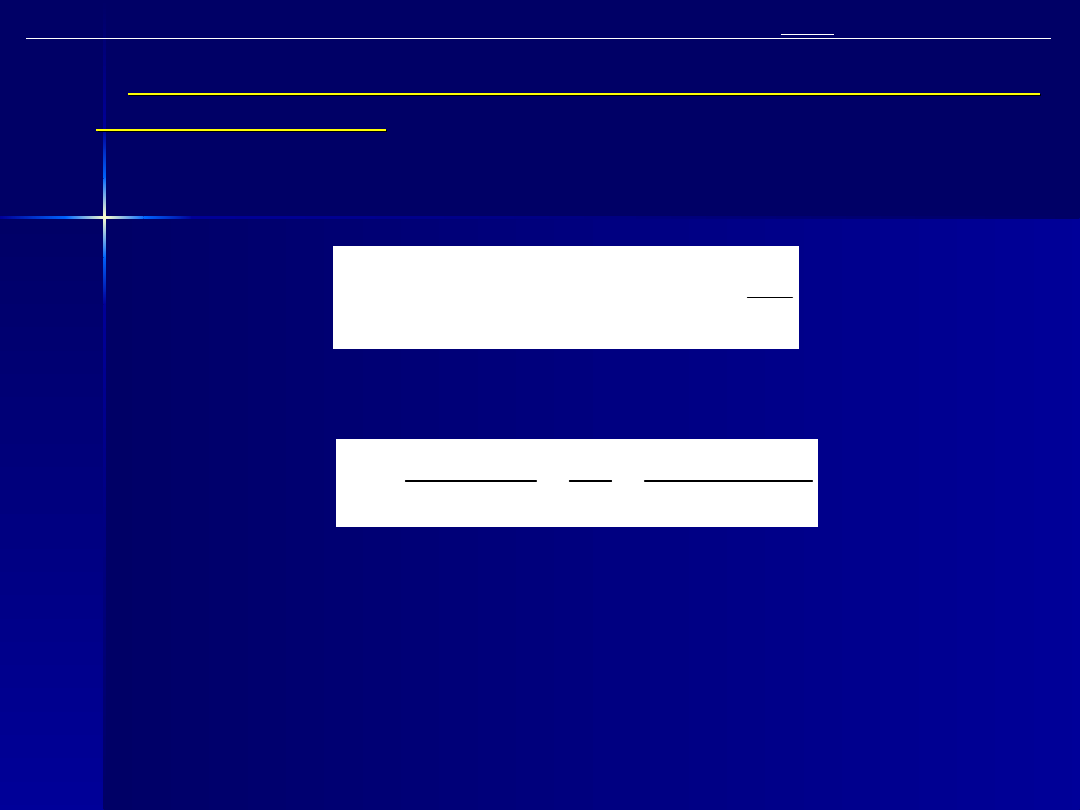
Różnica entalpii i

wz

- i

sk

jest praca zużyta na pompowanie wody do kotła,

wyrażoną w jednostkach ciepła. Przy założeniu uproszczenia i

wz

= i

sk

uzyskuje się postać:

wz

a

t

i

i

i

i







1

2

1



przy czym: i

1

– i

2a

= H

a

stanowi tzw. izentropowy (adiabatyczny) spadek

entalpii przy rozprężaniu pary w turbinie idealnej.

Sprawność i wskaźniki techniczno-ekonomiczne bloku

Sprawność i wskaźniki techniczno-ekonomiczne bloku

kondensacyjnego

kondensacyjnego

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

15

Sprawność ogólną bloku brutto można określić iloczynem
sprawności poszczegól-nych elementów biorących udział w procesie
wytwarzania energii i wyraża się zale-żnością:

B

g

g

m

w

t

r

k

bb

Q

P





























Sprawność kotła η

k

ujmuje straty ciepła powstające wskutek niedoskonałości konstrukcyjnych:



k

B

k

B

k

B

Dk

k

wz

B

r

Q

Q

Q

Q

Q

D

i

i

D W













(

)

w której : Q

B

- strumień energii w paliwie doprowadzonym do paleniska kotła, kJ/s;

ΔQ

k

- strumień strat energii w kotle, kJ/s;

Q

k

- strumień energii w parze wypływającej z kotła, kJ/s;

D

Dk

- strumień masy pary (wydajność kotła), kg/s;

i

k

- entalpia początkowa pary (pary za kotłem), kJ/kg;

D

B

- strumień masy paliwa, kg/s;

W

r

- wartość opałowa paliwa, kJ/kg.

Sprawność i wskaźniki techniczno-ekonomiczne bloku

Sprawność i wskaźniki techniczno-ekonomiczne bloku

kondensacyjnego cd.

kondensacyjnego cd.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

16

Sprawność rurociągów uwzględnia straty ciepła w rurociągach
przesyłowych, spowodowane niedoskonałością izolacji termicznej
oraz stratami ciśnienia przy przepływie pary, określa się ją
zależnością:



r

k

r

k

t

k

Dt

wz

Dk

k

wz

Q

Q

Q

Q

Q

D i

i

D

i

i















(

)

(

)

1

gdzie: ΔQ

r

- strumień energii w rurociągach, kJ/s;

Q

t

- strumień energii w parze doprowadzonej do turbiny,

kJ/s;

D

Dt

- strumień masy pary wpływającej do turbiny, kg/s.

Sprawność teoretyczną obiegu określa się wzorem :



t

a

wz

i

i

i

i







1

2

1

przy czym: i

1

- entalpia pary za kotłem, równa w układzie idealnym

(teoretycznym)
entalpii pary przed turbiną, kJ/kg;
i

2a

- entalpia pary po izentropowym jej rozprężaniu w

turbinie, kJ/kg;
i

wz

- entalpia wody zasilającej kocioł, kJ/kg.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

17

Sprawność i wskaźniki techniczno-ekonomiczne bloku

Sprawność i wskaźniki techniczno-ekonomiczne bloku

kondensacyjnego cd.

kondensacyjnego cd.

Sprawność wewnętrzną turbiny można wyrazić następującą zależnością:



w

a

i

i

i

i







1

2

1

2

gdzie: i

2

- entalpia końcowa rozprężania rzeczywistego politropowego, kJ/kg.

Sprawność mechaniczna uwzględnia straty mechaniczne w turbinie:



m

u

w

u

Dt

P

P

P

D i

i







(

)

1

2

gdzie: P

u

- moc użyteczna na wale, kW;

P

w

- moc wewnętrzna (rozwijana przez wirnik turbiny),

odpowiadająca pracy
strumienia pary D

Dt

rozprężającego się od i

1

do i

2

, kW.

Straty w prądnicy, obejmujące straty elektryczne w uzwojeniach i
w żelazie oraz straty mechaniczne w prądnicy, są określone wzorem:



g

g

u

P
P



przy czym: P

g

- moc elektryczna uzyskiwana na zaciskach prądnicy, kW.

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

18

Współczynnik potrzeb

Współczynnik potrzeb

własnych

własnych

Zużycie mocy przez urządzenia potrzeb własnych (głównie
napędy urządzeń pomocniczych, takich jak pompy. wentylatory,
młyny) P

pw

określa się przeważnie na podstawie jego udziału w

mocy wytworzonej brutto, jako:

 

P

P

pw

g

Moc netto oddawaną do sieci można wtedy określić zależnością:

P P P

P

n

g

pw

g

 





(

)

1 

Wyrażenie (1 – ε) = P

n

/P

g

ma charakter sprawności

uwzględniającej zużycie mocy przez urządzenia potrzeb własnych
bloku. Uwzględniając je trzymuje się wyrażenie na sprawność bloku
netto które można zapisać następująco:

)

1

(

































g

m

w

t

r

k

B

n

bn

Q

P

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

19

Podstawowe jednostkowe wskaźniki określające wydajność

Podstawowe jednostkowe wskaźniki określające wydajność

turbozespołu

turbozespołu

Równanie bilansu energetycznego turbozespołu można zapisać następująco:

D i

i

P

Dt

m g

g

(

)

1

2





 

Z powyższego równania określić można strumień masy pary
wpływającej do turbiny (natężenie dopływu pary do turbiny)
wzorem:

D

P

i

i

Dt

g

m g





(

)

1

2

 

Po podzieleniu obydwu stron powyższego równania przez moc
prądnicy P

g

otrzymuje się wskaźnik jednostkowego zużycia pary

przez turbinę:

d

D

P

i

i

t

Dt

g

m g







1

1

2

(

) 

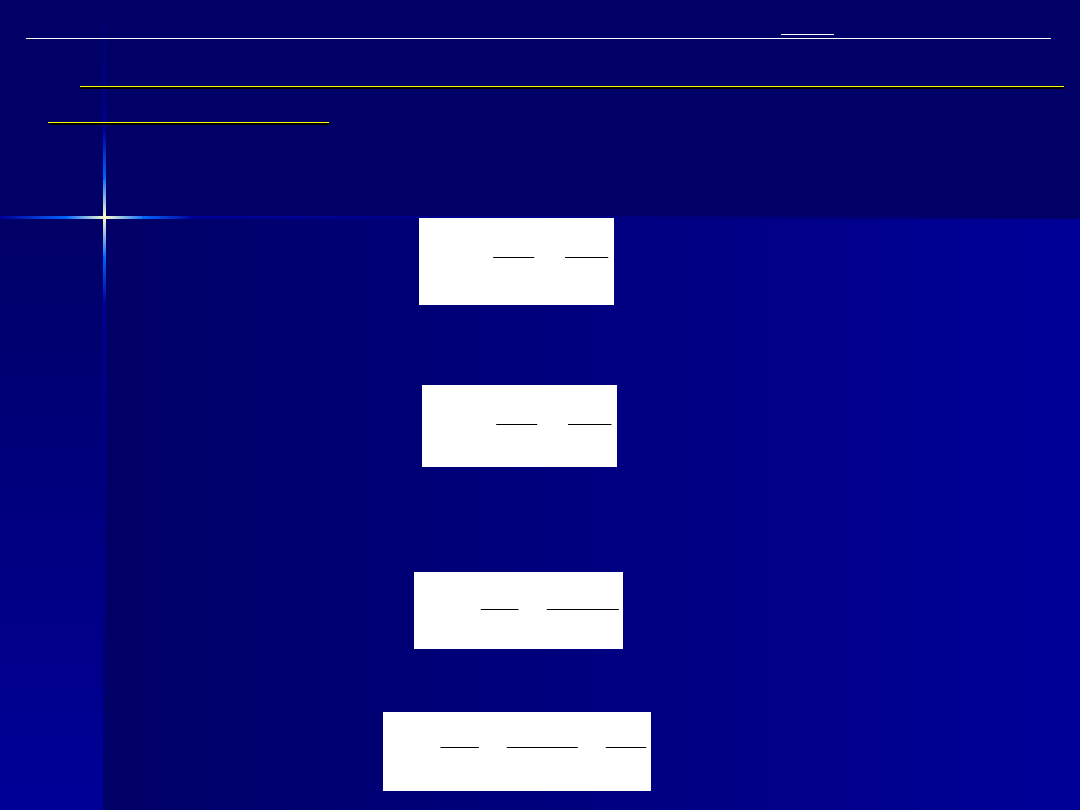
Wskaźnik jednostkowego zużycia ciepła przez turbozespół można określić zależnością:

q

Q

P

D i

i

P

d i

i

t

t

g

Dt

wz

g

t

wz











(

)

(

)

1

1

Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

20

Wskaźnik jednostkowego zużycia energii chemicznej paliwa
(ciepła dostarczanego do kotła), odniesiony do mocy brutto można
określić się wzorem:

Podstawowe jednostkowe wskaźniki określające wydajność

Podstawowe jednostkowe wskaźniki określające wydajność

turbozespołu cd.

turbozespołu cd.

q

Q

P

Bb

B

g

bb





1



Wskaźnik jednostkowego zużycia energii chemicznej paliwa netto
można wyrazić zależnością

:

q

Q

P

Bn

B

n

bn





1



Strumień masy paliwa (zużycie paliwa) dostarczonego do kotła
można, na podstawie wcześniejszych zależności określić jako:

D

Q

W

P

W

B

B

r

g

bb

r







Stąd wskaźnik jednostkowego zużycia paliwa brutto przez blok :

b

D

P

W

q

W

b

B

g

bb

r

Bb

r







1



Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

21

Podstawowe jednostkowe wskaźniki określające wydajność

Podstawowe jednostkowe wskaźniki określające wydajność

turbozespołu cd.

turbozespołu cd.

Natomiast wskaźnik jednostkowego zużycia paliwa netto:

b

D

P

W

q

W

b

B

n

bn

r

bn

r







1



W celu umożliwienia porównywania sprawności i wskaźników
jednostkowego zużycia ciepła i paliwa przez bloki zużywające paliwa
o różnych wartościach opałowych wprowadzono pojęcie paliwa
umownego, którego wartość opałową przyjęto jako W

u

= 29300

kJ/kg (7000 kcal/kg).
Wskaźniki jednostkowego zużycia paliwa umownego brutto i
netto wyrażają się zależnościami:

b

W

q

W

ub

bb

u

Bb

u





1



b

W

q

W

un

bn

u

Bn

u





1



Przedmiot: Podstawy elektroenergetyki, Temat: Energetyka konwencjonalna

22

Podstawowe jednostkowe wskaźniki określające wydajność

Podstawowe jednostkowe wskaźniki określające wydajność

turbozespołu cd.

turbozespołu cd.

Tablica 1. Osiągane wartości sprawności przetwarzania energii w elektrowniach
parowych

Sprawność

Oznacze

nie

Wartości

osiągane

w

elektrowni

ach

krajowych

Maksymal

ne

wartości

osiągane

w świecie

Kotła

Rurociągów

Teoretyczna obiegu

Wewnętrzna turbiny

Mechaniczna

turbozespołu

Prądnicy

Ogólna bloku (brutto)

η

k

η

r

η

t

η

w

η

m

η

g

η

bb

0,7 ÷ 0,9

0,98 ÷

0,99

0,37 ÷

0,44

0,70 ÷

0,87

0,96 ÷

0,985

0,95 ÷

0,98

0,34 ÷

0,38

0,935

0,99

0,54

0,91

0,99

0,99

0,45