Ryzyko

• Ryzyko oznacza możliwość osiągnięcia wartości końcowej

kapitału (inwestycji, instrumentu finansowego) różniącej się

od wartości oczekiwanej.

• Działanie w warunkach ryzyka, dotyczy podejmowania

decyzji odnośnie do zdarzeń, które mogą wystąpić z

określonym prawdopodobieństwem.

• Zatem o tym, że ktoś działa w warunkach ryzyka, można

mówić wtedy, kiedy jego decyzja dotyczy zdarzeń, które

mogą wystąpić z określonym prawdopodobieństwem. Jest

ono liczbą z przedziału [0,1], która pokazuje, ile razy dane

zdarzenie wystąpi, jeśli określona sytuacja powtórzy się

wielokrotnie: p = m/M , gdzie: p – prawdopodobieństwo

wystąpienia badanego zdarzenia, m – liczba powtórzeń

zdarzenia, M – liczba prób.

Niepewność

• Niepewność jest czymś innym niż ryzyko. Problem

niepewności występuje w rzeczywistości ekonomicznej, kiedy

podejmujący decyzję nie znają konsekwencji swojego wyboru.

• Jeśli niemożliwe jest określenie prawdopodobieństwa jakiegoś

zdarzenia, to działalność odbywa się w warunkach

niepewności.

• Niejednokrotnie w procesie podejmowania decyzji można

oszacować wielkości zdarzeń (stopa zwrotu z inwestycji w

różnych wariantach projektu), ale niemożliwe jest przypisanie

im prawdopodobieństwa.

• Ryzyko można określić jako mierzalną niepewność.

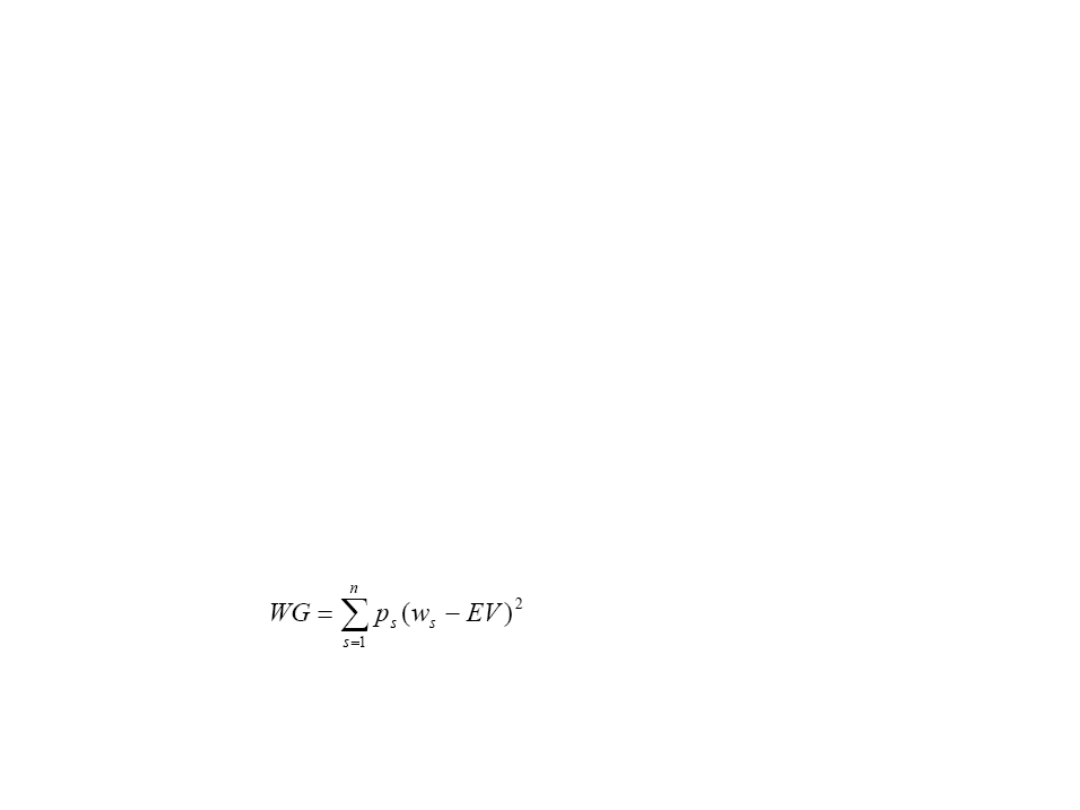
Zachowania w przypadku ryzyka i

niepewności

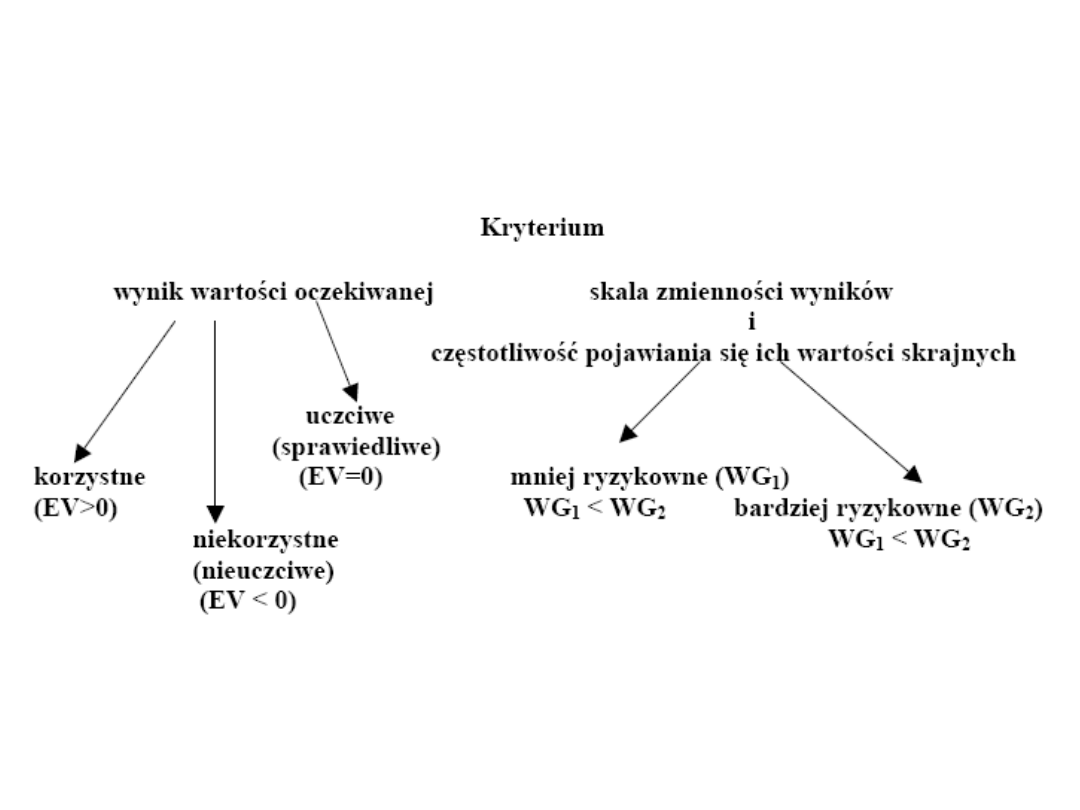
Grami nazywa się sytuacje, kiedy wyniki o pewnej wartości pieniężnej

pojawiają się z różnym prawdopodobieństwem.

Wartość oczekiwana z gry, czyli średnia wypłata uzyskiwana przy

wielokrotnym powtarzaniu gry:

EV (w1, w2, p1, p2) = p1·w1 + p2·w2,
gdzie: w1 i w2 – wypłaty; p1, p2 –
prawdopodobieństwo, z którym wystąpi wypłata.

Za dokładną miarę zmienności wyników gry (ryzykowność gry) uznaje

się wariancję gry (WG). Jest ona sumą podniesionych do kwadratu

odchyleń wyników gry od jej wartości oczekiwanej, zważonych

prawdopodobieństwem wystąpienia tych wyników, czyli

• gdzie: ws –wynik gry, ps – prawdopodobieństwo ich wystąpienia.

Rodzaje gier

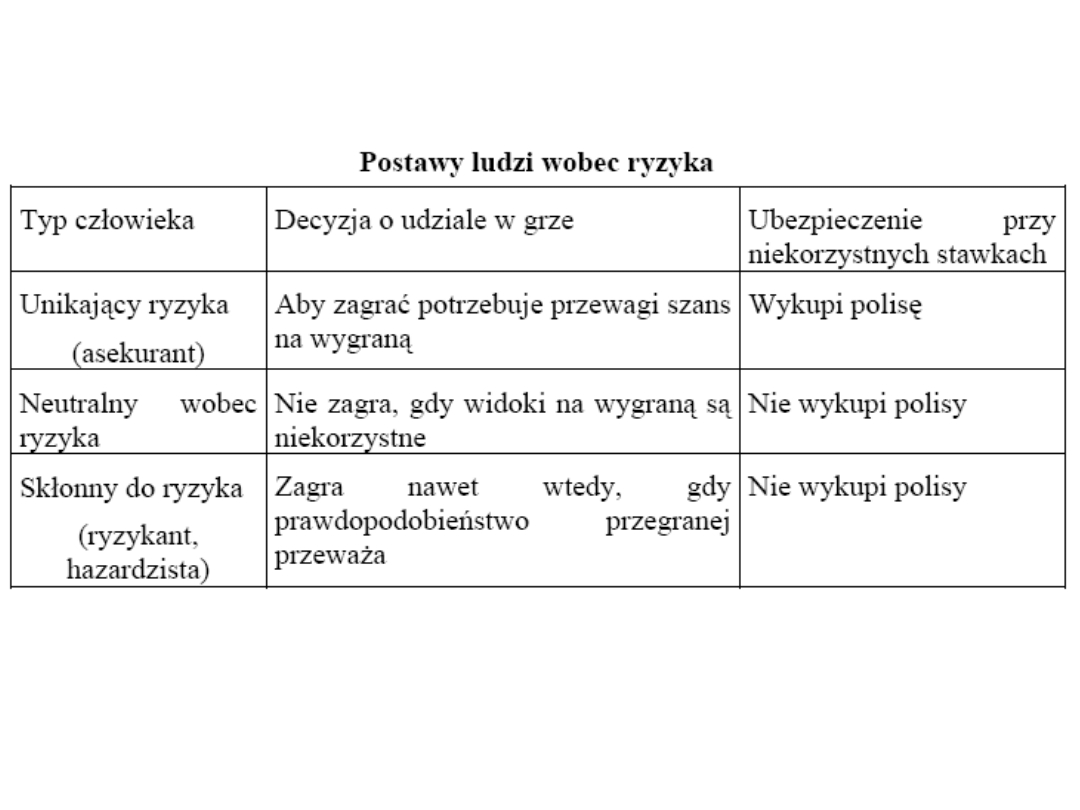
• Preferencje względem ryzyka nie są stałe i

zmieniają się w zależności od tego, czy decydent
działa w warunkach zysków, czy też w warunkach
strat (framming effect)! [Tversky, Kahneman
1981]

Awersja do strat

1. Podmiot ma do wyboru dwie możliwości:

• dochód 3000 bez ponoszenia ryzyka
• dochód 4000 z prawdopodobieństwem 0,75 lub 0 z

prawdopodobieństwem 0,25.

Wartość oczekiwana w obu przypadkach wynosi 3000.

Okazuje się, że większość ludzi wybiera sytuację

pierwszą, charakteryzującą się awersją do ryzyka.

2. Podmiot ma do wyboru dwie możliwości:

• pewna strata 3000
• strata 4000 lub 0, przy czym prawdopodobieństwo

straty 4000 wynosi 0,75, a prawdopodobieństwo straty 0

wynosi 0,25.

Można wyciągnąć wniosek, że w przypadku zwiększania się

kapitału (dochodu) podmiot charakteryzuje się awersją

do ryzyka, a w przypadku zmniejszania się kapitału

(dochodu), czyli straty charakteryzuje się skłonnością do

ryzyka. Zjawisko to nazwano awersją do strat.

Przykład a: Problem choroby

azjatyckiej (kontekst zysków)

W pewnym mieście wybuchła epidemia groźnej
choroby azjatyckiej. Specjaliści twierdzą, że jeśli nie
zostaną podjęte żadne działania, to z jej powodu umrze
600 zarażonych osób. Eksperci proponują dwa
programy ratunkowe i musimy wybrać jeden z nich.
•Program 1; Jeśli wybierzemy ten program, na pewno
zostanie uratowanych dokładnie 200 osób.
•Program 2: Jeśli wybierzemy ten program, to z
prawdopodobieństwem równym 1/3 uda się uratować
wszystkie zarażone osoby, a z prawdopodobieństwe3m
2/3 nie uda się uratować nikogo.

Przykład b: Problem choroby

azjatyckiej (kontekst strat)

W pewnym mieście wybuchła epidemia groźnej
choroby azjatyckiej. Specjaliści twierdzą, że jeśli nie
zostaną podjęte żadne działania, to z jej powodu
umrze 600 zarażonych osób. Eksperci proponują dwa
programy ratunkowe i musimy wybrać jeden z nich.
•Program 1; Jeśli wybierzemy ten program, na
pewno umrze dokładnie 400 osób.
•Program 2: Jeśli wybierzemy ten program, to z
prawdopodobieństwem równym 1/3 nikt nie umrze, a
z prawdopodobieństwe3m 2/3 umrą wszystkie
zarażone osoby.

Przykład c: Problem doradcy

inwestycyjnego (kontekst zysków)

Jesteś doradcą finansowym. Twój klient zainwestował
60000 zł w portfel akcji i wkrótce potem nastąpił wielki
krach giełdowy. Masz do wyboru dwie strategie i jedną z
nich możesz zaoferować swojemu klientowi.
•Jeśli wybierzesz strategię A, to Twój klient na pewno
zachowa dokładnie 20000 zł.
•Jeśli wybierzesz strategię B, to z
prawdopodobieństwem równym 1/3 twój klient uratuje
całą kwotę, czyli 60000 zł oraz z prawdopodobieństwem
równym 2/3 twój klient nie uratuje niczego.
Na podstawie tych informacji dokonaj wyboru: czy
zarekomendujesz mu strategię A, czy raczej strategię B?

Przykład d: Problem doradcy

inwestycyjnego (kontekst strat)

Jesteś doradcą finansowym. Twój klient zainwestował
60000 zł w portfel akcji i wkrótce potem nastąpił wielki
krach giełdowy. Masz do wyboru dwie strategie i jedną z
nich możesz zaoferować swojemu klientowi.
•Jeśli wybierzesz strategię A, to Twój klient na pewno
straci dokładnie 40000 zł.
•Jeśli wybierzesz strategię B, to z
prawdopodobieństwem równym 1/3 twój klient nic nie
straci, oraz z prawdopodobieństwem równym 2/3 twój
klient straci całe 60000 zł.
Na podstawie tych informacji dokonaj wyboru: czy
zarekomendujesz mu strategię A, czy raczej strategię B?

Gra 1.

Rzucamy kością do gry. Jeśli wypadnie liczba

nieparzysta, płacimy 150zł, jeśli wypadnie 6 –
otrzymujemy 600zł, jeśli wypadnie 2 lub 4 nie
otrzymujemy ani nie płacimy nic.

Gra 2.

Obstawiamy 100zł na „czerwone” w ruletce (37 pól:

36 pól kolorowych oraz 0). Jeśli wypadnie czarne –
tracimy 100zł, jeśli czerwone – zyskujemy
dodatkowe100zł, jeśli wypadnie 0 – tracimy
połowę obstawienia.