1

8. The special theory of

relativity

Relativity is connected with the measurement of where and
when events take place, and how these events are measured in
reference frames that are moving relative to one another. It
gives a new look at the notion of simultaneity.

The theory called „special” means that it holds only for the
inertial reference frames in which Newton’s laws are valid
(the theory concerning the frames which undergo gravitational
acceleration is known as general theory of relativity) .

8.1. Einstein’s Postulates

In 1905 Albert Einstein introduced two postulates:

1. The Relativity Postulate: The laws of physics are the same
for observers in all inertial reference frames.

2. The Speed of Light Postulate: The speed of light in
vacuum has the same value c in all directions and in all inertial
reference frames.

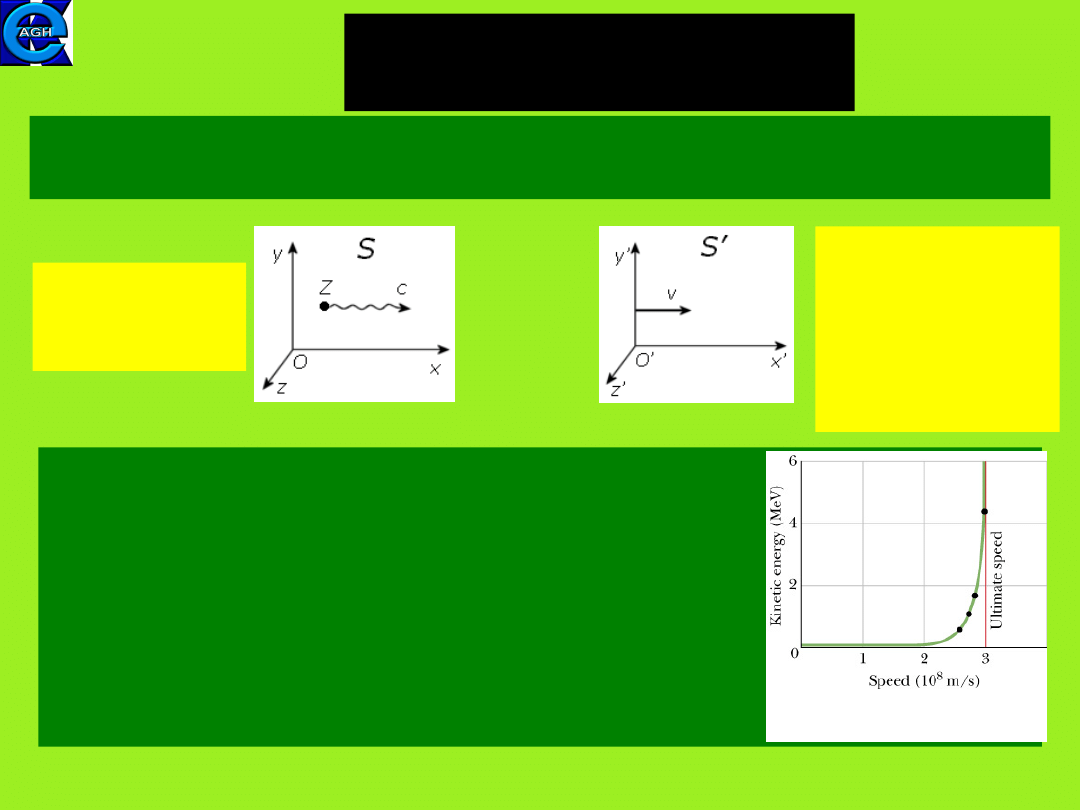
2

The speed of light,

cont.

Many experiments have shown that the speed of light does not
depend on the move either a light source or an observer.

The speed of light has a limit. W. Bertozzi (1964)
accelerated electrons measuring their speed and kinetic
energy. Electrons reached the speed
0.999 999 999 95c but always less than the ulimate value
c = 299 792 458 m/s; the energy increased toward very
large values.
We essentially use the approximate value of the light speed
in vacuum as c = 3.0 · 10

8

m/s.

in the frame S
the source Z
is at rest

in the frame S’
the source Z is
moving but the
measurement of
light speed also
gives c

3

8.2. The Lorentz transformation

equations

Suppose that at time instant t = t’ =
0 we emit from the common origin
of both frames

the light flash

moving at speed c.

The wavefront of a light wave is a sphere of the radius

in frame S
in frame S’

In S this sphere is described by

(8.1a)

Consider two reference frames S and S’, where S’ is moving in
respect to S with constant velocity

v

along the x – axis.

We wish to find the transformation (relations between x,y,z and
t in frame S in relation to x’,y’,z’ and t’ in frame S’), for which
the speed of light does not depend on the move either the light
source or the observer.

ct

r 

t

c

r







2

2

2

2

2

t

c

z

y

x







4

The Lorentz transformation,

cont.

In S’:

(8.1b)

Applying to Eq.(8.1a) the clasical Galilean Transformation (GT)
one obtains:

(8.2)

Eq.(8.2) is in contradiction to (8.1a).
Conclusion:

GT is not valid if the second Einstein’s postulate is true

(the speed of light is the same in both frames).
We are looking for the transformation, which converts (8.1b)
into (8.1a) and reduces to GT for .

This transfotmation should be:

• simple for y’ and z’ to convert y’

2

and z’

2

without changes

to y

2

and z

2

.

• linear vs. x and t to obtain the spherical wavefront

• time should be also transformed to cause vanishing of
extra terms
in Eq.(8.2)

2

2

2

2

2

t

c

z

y

x















2

2

2

2

2

2

2

2

t

c

z

y

t

v

xvt

x











0



c

/

v

5

The Lorentz transformation,

cont.

In the first attempt we introduce the constant

f

(8.3)

Substituting (8.3) into (8.1b) one obtains

(8.4)

The terms comprising xt should disappear

then

(8.5)

Substituting for

f

into (8.4) we have

(8.6)

Eq.(8.6) transforms to (8.1a) if we reduce the unnecessary
multiplication term

fx

t

t

z

z

y

y

vt

x

x

































2

2

2

2

2

2

2

2

2

2

2

2

2

x

f

c

ftx

c

t

c

z

y

t

v

xvt

x















2

2

0

2

2

c

v

f

ftx

c

xvt













x

c

v

t

t

2









































2

2

2

2

2

2

2

2

2

1

1

c

v

t

c

z

y

c

v

x





2

2

1

c

/

v



6

The Lorentz transformation,

cont.

The final shape of the transformation is then

(8.7)

For LT reduces to GT, what was expected.

Introducing the replacements:
the LT equations can be rewritten as:

(8.8)

or in the inverse form:

(8.9)

The inverse transformation (8.9) was obtained from (8.8) by
reversing the sign of

v

.













2

2

2

2

2

1

1

c

v

x

c

v

t

t

z

z

y

y

c

v

vt

x

x

























Lorentz transformation (LT) equations
valid at all physically possible speeds

0



c

/

v

)

(

,

c

v

1









)

(

,

1

1

1

2



























 



















c

x

t

t

z

z

y

y

ct

x

x

















































c

x

t

t

z

z

y

y

t

c

x

x









7

8.3. Consequences of the Lorentz

transformation

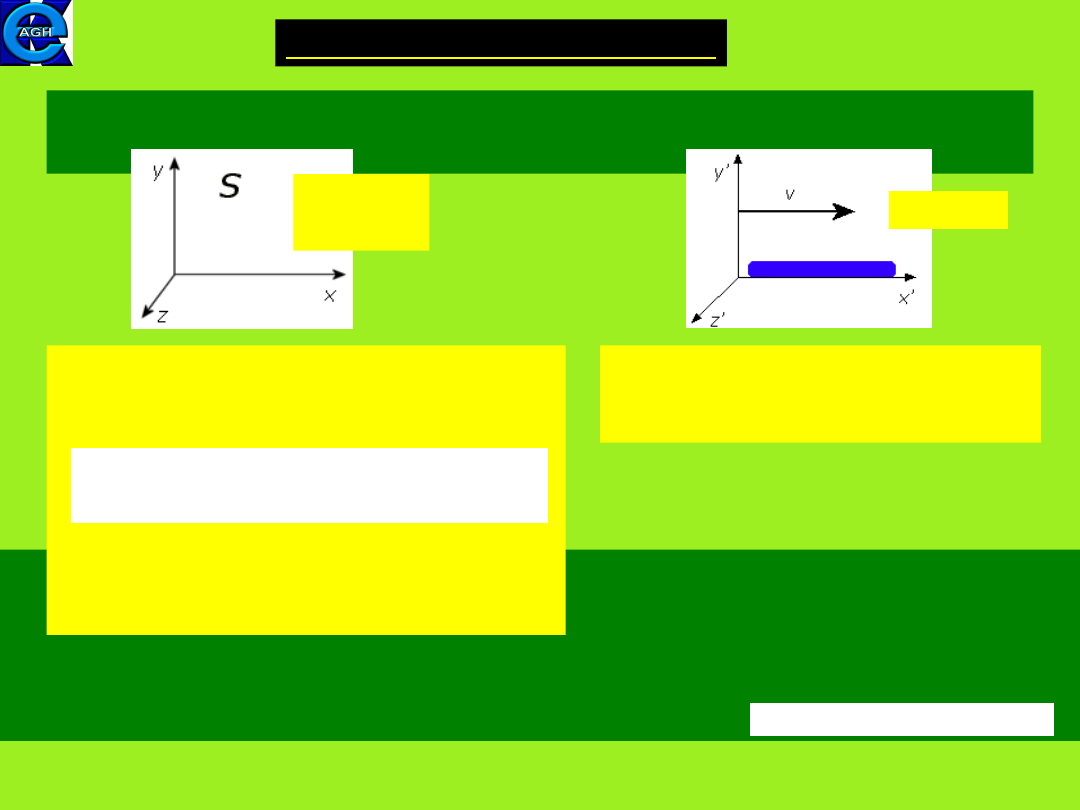
We measure the length of a rod moving in the
diection of its length.

The length L of a moving rod decreased (length contraction).
The measurements in directions y or z give results independent of velocity.

Rod at rest in

a resting frame S

The observer in S measures
the coordinates of a rod end points
which are independend of time.
The length is: L

0

= x

2

– x

1

The observer in S’ has to measure
the coordinates of a rod end points at the same
instant of time t’. So the inverse Lorentz
transformation is used:

Subtracting on both sides one obtains

or

because >1









'

'

'

'

ct

x

x

ct

x

x

















2

2

1

1





0

1

2

1

2

L

L

x

x

x

x

'

'















0

0

L

/

L

L







8.3.1. The relativity of length (length contraction)



8

The same result as previously we obtain if the rod rests in a
moving frame S’.

It is not important in which reference frame we place the rod, only whether it is
moving in relation to the observer or not (in diection of its length). The measurement
of length of a moving object gives lower value. The essential role plays here the

simultaneity

. Two simultaneous events in S (Δt=0) separated by

Δ

x, are separated

in S’ both in space and in time. From LT one obtains easily:

The observer in S’ measures
the coordinates of a rod end points
which are independend of time.

The observer in S has to measure the
coordinates of a rod end points at the
same instant of time t. So we use the
transformation:

Length contraction, cont.













L

L

x

x

x

x

ct

x

x

ct

x

x

'

'

'

'









































0

1

2

1

2

1

1

2

2

L = x

2

–

x

1

'

'

x

x

L

1

2

0





x

t

c

,

x

x

























9

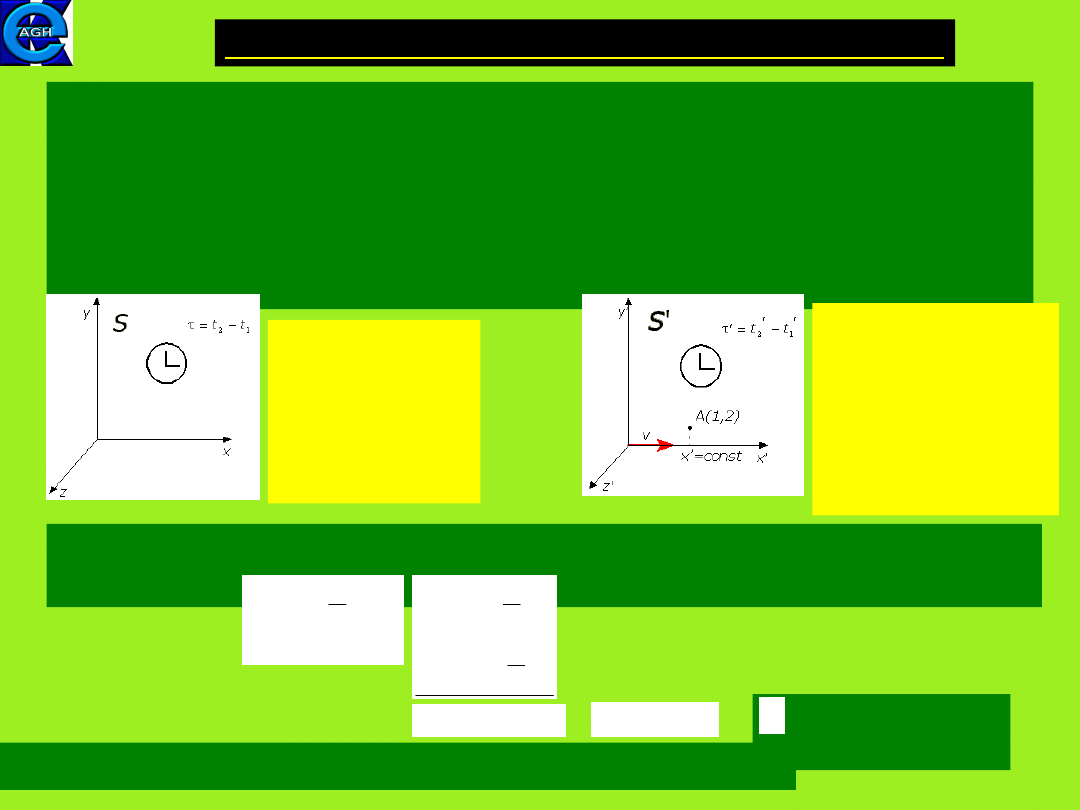
The problem concerns the dilation (expansion) of time
measured by the moving clocks. The time interval betwen two
events occuring at the same location measured by the clock
placed in this location is called the

proper time interval

.

Measurements of the same time interval from any other
inertial reference frame are always greater.

We use the transformation for which

Δ

t’ time interval occures

for x’ = const, so the inverse LT

The events occur
in point A, at rest
in S’. The clock is
placed at the
same location, i.e.
is at rest in
relation to A(1,2).

The clock in S
moves in
relation to point
A(1,2) in which
the events
occur.

8.3.2. The relativity of time (time dilation)























x

c

t

t









































x

c

t

t

x

c

t

t

'

'









2

2

1

1





'

'

t

t

t

t

1

2

1

2









0















- the proper
time

0



The proper time is the minimal time between events.

10

1. The lifetime of mesons π

+

It is known that meson π

+

is an unstable particle and decays

giving a meson μ

+

and a neutrino

The lifetime of π

+

(the proper time, measured in a frame in

which the meson rests) is 2.5·10

-8

s. What is the lifetime

observed in a laboratory, if mesons are moving with a speed of
v = 0.9 c.

In this way the meson covers more than two times longer
distance vs. that obtained from non-relativistic calculations
(correct for speeds much less than c).

Time dilation - examples

n

0

0













s

,

,

s

.

8

8

2

0

0

10

7

5

81

0

1

10

5

2

1































2. The paradox of twins
What will be the age of one of the twins sent in space after the
birth with velocity
v = 0.9 c, when he comes back after 20 years according to the
age of a twin in the Earth.

For v

= 0.5c τ

0

= 17.3 years.

years

,

c

c

,

7

8

9

0

1

20

1

2

2

0



































11

Time dilation – examples, cont.

3. Macroscopic Clocks. Super precision atomic clocks (large
systems) flown in airplanes (β ~7x10

-7)

enabled an experiment on

a macroscopic scale. U. Maryland carried out an experiment
using an atomic clock flying over Chesapeake Bay (round and
round) and checked the time dilation within 1% of predictions.

If the clock on the U. Maryland flight registered
15.00000000000000 hours as the flight duration, how much
would a clock that stayed on earth (lab frame) have measured
for the duration? More or less? Does it matter whether airplane
returns to same place?

(

) (

)

7

2

0

8

0

1

if

7 10

1.000000000000245

1

1.000000000000245 15.00000000000000 hr

15.00000000000368 hr

1 10 s!

t

t

t

t

b

g

b

g

-

-

= �

�

=

=

-

D = D =

=

D - D = �

12

8.4. The relativity of

velocities















 











c

x

t

t

ct

x

x









A particle has velocity

u

in the frame S.

What velocity is measured by the observer in S’,
which is moving with velocity

v

relative to S.

From the Lorentz transformation one gets





u

c

v

v

u

u

c

c

u

c

dx

dt

cdt

dx

t

d

x

d

'

u

2

1

1































































 











c

dx

dt

t

d

cdt

dx

x

d









Using the definition of

u’

we have

the relativistic velocity
transformation

For one obtains from (8.10) the known Galilean velocity transformation:

(8.10)

0



c

/

v

v

u

'

u





13

The relativity of velocities,

cont.

Example

What is the speed of a photon in a reference frame at rest if it has velocity

c

in a frame moving with velocity

v

relative to the resting frame. A photon

moves parallel to the x axis.

In this case
For the Galilean transformation we would obtain

what is in contradiction to the Einstein’s second postulate.

From the relativistic velocity transformation (8.10) one obtains

in accordance with the relativistic theory.
The obtained result also indicates that it is impossible to find such a reference frame
in which a photon would be at rest. Even for

v = -c, u = c

.

c

'

u 

c

v

u









c

v

c

v

c

c

c

c

v

v

c

'

u

c

v

v

'

u

u





















2

2

1

1

14

8.5. Doppler effect for

light

In the classical case of mechanical waves the frequency

f’

detected by the observer is equal

(8.11)

where

f – the proper frequency of the source
v – velocity of the wave in the medium
v

0,

v

z

– velocities of the observer and the source

respectively

(the signs of velocities are positive if are

directed

similarly to v).

In the case of light we expect that the change in frequency
connected with the Doppler effect will depend on the relative
velocity v of source vs observer only.

There is no air (ether) for the

relative move of light.

(8.12)

If source and detector move toward one another

→ 

As is expected only the ratio of relative velocity of source and
detector to the velocity of light



=

v/c

is important.

z

v

v

v

v

f

f









0













1

1

f

f

15

Doppler effect for light,

cont.

Eq.(8.12) for low speeds (



« 1) can be expanded in a series and approximated as

(8.13)

Taking into account that f = c/



one can obtain from (8.13)

(8.14)

Introducing the Doppler wavelength shift one obtains from (8.14)



(8.15)

Eq.(8.15) is used in astronomical observations to determine how fast the light
sources are moving and in which direction (toward or away from the observer).
The theory of the universe expansion was approved by observation of the so
called red shift (

’>



)

1

(

)

2

1

1

(

2



















f

f

f

)

1

(

'











c

c













'

c

v









16

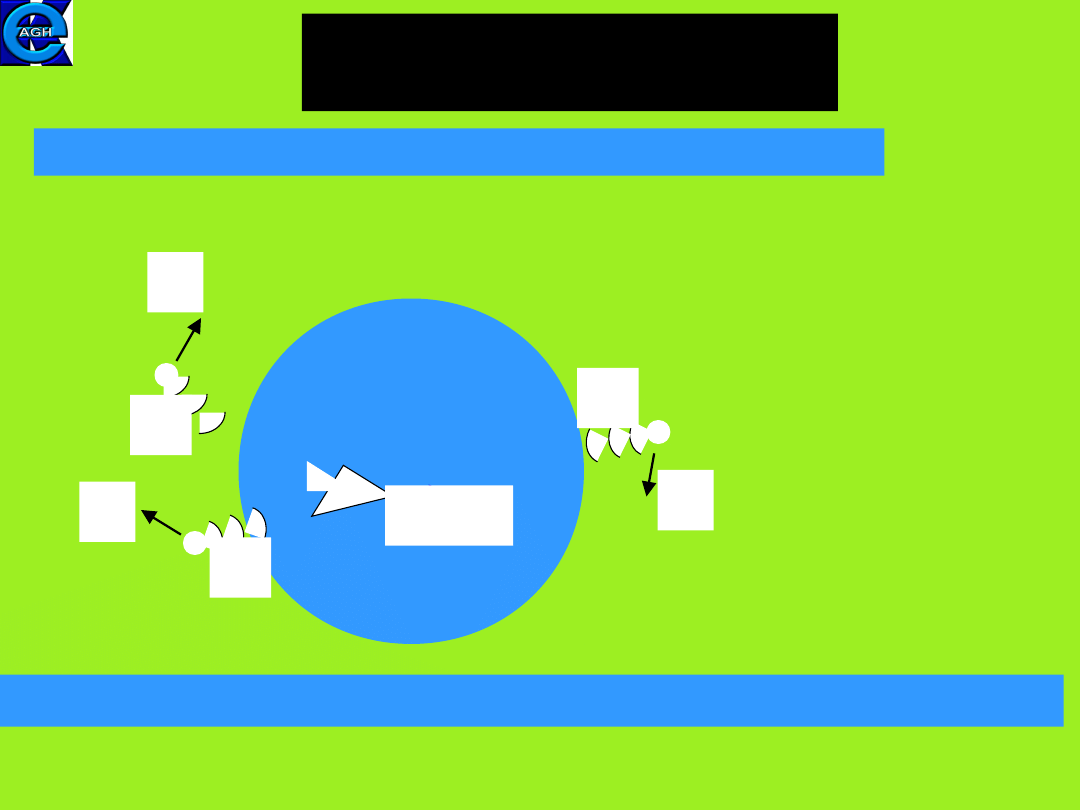
Doppler effect for light,

cont.

v

1

v

2

v

3

v

airplane

f

01

f

02

f

03

The NAVSTAR Navigation System

Given v

1

, v

2

, v

3

, f

01

, f

02

, f

03

, and measured f

1

, f

2

, f

3

, can determine v

airplane

.

17

8.7. Relativistic

dynamics

Relativistic momentum
The classical (nonrelativistic) momentum of a particle

(8.16)

is not conserved in collisions of particles moving with high
speeds. When we
define the momentum as

(8.17)

it becomes invariant vs. Lorentz transformation. The relativistic
momentum can then be written as

where

(8.18)

m – relativistic mass of a particle with rest

mas m

0

and velocity v







v

m

p

0



0

m

p 



 







v

v

m

p

 



0

m

v

m



The dependence between mass and velocity was also
proved experimentally; in practice for

2

,

0

/ 

c

v

0

m

m 

18

Relativistic dynamics,

cont.

Relativistic Energy
Elementary change in kinetic energy caused by the work of a
net force

F

is

(8.19)

The total change in energy is obtained by integrating eq.(8.19)
by parts as below

In this way one obtains























































v

m

d

v

v

p

d

dt

v

dt

p

d

r

d

dt

p

d

r

d

F

dW

dE

k









wdu

uw

udw





2

0

2

2

0

2

0

2

2

2

2

0

2

0

2

2

2

2

2

0

0

2

2

0

2

0

2

2

2

0

2

2

2

2

2

2

0

2

0

2

2

2

2

0

2

0

2

0

2

0

0

0

1

1

1

1

1

1

1

1

2

2

1

2

1

2

2

1

c

m

c

m

c

m

c

m

c

m

c

v

c

m

c

m

mv

c

v

c

m

mv

c

v

c

v

d

c

m

mv

c

v

dv

c

v

c

m

mv

c

v

vdv

m

mv

v

d

v

m

v

m

v

v

m

d

v

E

v

v

v

v

v

v

v

k













































































































































































19

Relativistic energy, cont.

and thus we have

(8.20)

It is interesting to prove if eq.(8.20) valid for a relativistic
particle transforms into
the known classical expression for kinetic energy of a particle
moving with .
First we rewrite Eq.(8.20) as

(8.20a)

The expression

where ,

can be expanded into a series:

For only the term to the first power is relevant, since the
other terms are much smaller, hence

(8.21)





2

0

2

0

2

c

m

m

c

m

mc

E

k









c

v



































1

1

2

/

1

2

2

2

0

c

v

c

m

E

k







x

c

v





















1

1

2

/

1

2

2

2

2

c

v

x 



2

1

















 



...

x

!

n

n

...

...

x

!

x

x

n























1

1

1

2

1

1

1

2















1



x





x

x











1

1

20

Relativistic energy, cont.

Therefore, for the condition one obtains from (8.21)

(8.22)

what is a known classical expression for the kinetic energy.
From Eq.(8.20) it follows that the increase in kinetic energy
of a particle is connected with the inrease of its mass.
The total energy

E

of a particle is a sum of its kinetic energy

E

k

and a rest energy

m

0

c

2

(8.23)

Equation

(8.24)

states that a mass and an energy are equivalent. It is
one of the most important consequences of the theory of
special relativity. From (8.24) it follows that the change



m in a

mass is equivalent to the change



E in energy:

(8.25)

and also the energy can be converted into a mass:

1

/

2

2



c

v





2

2

1

2

1

1

1

1

2

0

2

2

0

2

2

0

2

1

2

2

0

v

m

c

m

c

m

c

m

E

k





























 





























2

0

2

c

m

E

mc

E

k







2

mc

E 

Comparison of
relativistic and classical
expressions for the
kinetic energy of an
electron with
experimental data (

x

)

 

2

c

m

E







2

c

E

m 





(8.26)

21

Relativistic energy, cont.

The conversions of mass into energy (and vice versa) are clearly
seen in nuclear
reactions.
We consider the reaction:

a particle a collides with a nucleus X producing another

nucleus Y which

emits a particle b

In reactions of this type the inertial mass (or the total energy) is
conserved

where:

m

01

…m

04

- rest masses

E

k1

…E

k4

- kinetic energies

Q – the energy of a reaction
if Q > 0 the energy is released (exothermic

reaction)

if Q < 0 the energy is absorbed (endothermic

reaction)

X + a Y
+ b



2

4

04

2

3

03

2

2

02

2

1

01

c

E

m

c

E

m

c

E

m

c

E

m

k

k

k

k

















 



2

2

1

4

3

04

03

02

01

c

E

E

E

E

)

m

m

(

m

m

k

k

k

k















2

04

03

02

01

c

Q

)

m

m

(

m

m









22

Nuclear reaction -

example

What is the energy released in the following nuclear reaction

For one mole we obtain the energy N

A

times higher (N

A

–

Avogadro’s number)

For comparison the chemical reaction of burning hydrogen in
oxygen gives the energy:

For chemical reactions the variation of a mass is then negligible
and the rest mass is conserved:

2

4

2

1

1

7

3

2

c

Q

He

H

Li







0

0186

0

2

2











u

,

m

m

m

c

Q

He

H

Li

MeV

MeV

u

c

m

Q

33

,

17

5

,

931

0186

,

0

2













mole

J

J

Q

mole

/

10

10

02

,

6

10

6

,

1

33

,

17

12

23

13















u – mass unit
1u is equivalent to 931.5 MeV
1 MeV = 10

6

eV = 1.6 ·10

-13

J

O

H

O

H

2

2

2

2

1





mole

J

Q

/

10

3

5





03

02

01

m

m

m



