Lista 2 (zajęcia 3 i 4)



1. Cząstka o masie m=2 kg porusza się w polu siły F , zależnej od czasu w następujący sposób:

 ˆ



 4sin

 6 12 ˆ

ˆ

 6 t

F

t i

t

j

e k N.

Przyjmując warunki początkowe:  ˆ  ˆ

ˆ



 ˆ

ˆ

r

5 i

2 j 3 k m, v

2 i 1 k m/s , znaleźć zależność

0

położenia i prędkości cząstki od czasu.

2. Jaka prędkość początkową v0 trzeba nadać ciału o masie m, aby wjechało na szczyt góry o długości d i kącie nachylenia α, jeśli współczynnik tarcia wynosi f? Oblicz czas trwania ruchu

3. Znaleźć i przedyskutować równania ruchu oraz równania toru cząstki o masie m i



ładunku q, poruszającej się w stałym, jednorodnym polu elektrycznym E . Obliczyć zmianę energii kinetycznej cząstki w zależności od jej położenia oraz czasu. Prędkość





początkowa v  0 , położenie początkowe r  0.

0

0

4. Samochód o masie m hamowany jest siłą F=-kv2. Jaką drogę przebędzie samochód, zanim prędkość jego zmaleje do połowy?

5. Znaleźć położenie, prędkość i tor kamienia rzuconego w polu grawitacyjnym Ziemi z prędkością początkową v0 pod katem  do poziomu, jeżeli jego początkowe położenie było zadane przez x0=y0=0. Określić składową normalna i styczna przyspieszenia kamienia w dowolnym punkcie toru.

6. Kula pistoletowa wystrzelona poziomo przebiła dwie pionowo ustawione kartki papieru, umieszczone w odległościach l1 = 20 m i l2 = 30 m od pistoletu. Różnica wysokości na jakich znajdują się otwory w kartkach wynosi h = 5 cm. Oblicz prędkość początkową kuli.

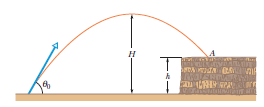
7. Jak pokazano na rysunku 4.48, kamień został

wrzucony na urwisko o wysokości h, przy czym

jego prędkość początkowa miała wartość 42 m/s i

była skierowana pod kątem 60° do poziomu.

Kamień upadł w punkcie A po 5,5 s od jego

wyrzucenia. Wyznacz: a) wysokość urwiska h, b)

wartość prędkości kamienia tuż przed dot arciem do punktu A, c) największe wzniesienie kamienia nad ziemię H.