23 FALE ELEKTROMAGNETYCZNE (5 stron) Falami elektromagnetycznymi nazywamy rozchodzące się w przestrzeni zaburzenia pola elektromagnetycznego.
Istnienie fal elektromagnetycznych wynika bezpośrednio z równań Maxwella. W duŜej odległości od źródeł pola czyli ładunków swobodnych i prądów elektrycznych, czyli dla ρ = 0 i j = 0 równania Maxwella mają postać:
∂
B
∂
rotE = −
D
rotH =
∂ t
∂ t
divD =
0
divB = 0
gdzie
D = εε E ε = 8
,
8 5 ⋅10 1
− 2 F / m
0
0
B = µµ H
µ = 4π ⋅10−7 H / m
0
0
Z równań Maxwella wynika, Ŝe wektory natęŜeń pól elektrycznego i magnetycznego (oraz wszystkie ich rzuty na osie układu współrzędnych kartezjańskich) w ośrodku jednorodnym, izotropowym i nieprzewodzącym spełniają równanie falowe: Dla ε = const
2
∂
∆ − εε µµ
E
E
= 0
0
0
2
∂ t
2
∂
∆ − εε µµ
H
H
= 0
0
0
2
∂ t
2
∆ ≡ ∇∇ = ∇ jest operatorem Laplace’a nazywanym teŜ laplasjanem. We współrzędnych kartezjańskich laplasjan równy jest:
∂2
∂2
∂2
∆ =
+
+
2
2
2
∂ x
∂ y
∂ z
Rozwi
ązaniem równania falowego jest dowolna funkcja argumentu τ = t − ( r ⋅ n) / v , która ma ciągłe drugie pochodne.
r n
E = f t −
n r = n x + n y + n z
v
x
y
z
Wartość τ opisuje fazę fali, n jest wektorem jednostkowym w kierunku rozchodzenia się fali a r wektorem połoŜenia danego punktu. Prędkość rozchodzenia się fali, v, spełnia warunek:
1
v 2 = εε
0µµ o
c
1
Stąd v =
gdzie c =
jest prędkością światła w próŜni, c = 2,997924562 m/s.
εµ
ε µ
0
0
Punkty o stałej wartości fazy tworzą powierzchnie stałej fazy opisane równaniem rn
τ = t −
= const .
v
Powierzchnie te rozchodzą się z prędkością v, którą nazywa się prędkością fazową fali.
x
W jednym wymiarze rozwiązanie równania falowego ma postać f t −
v
Fale elektromagnetyczne 23/
1
W określonej chwili czasu t powierzchnie stałej fazy dane są równaniem rn = const . JeŜeli wektor n ma stały kierunek, to powierzchnie stałej fazy są płaszczyznami prostopadłymi do n . Taką falę nazywa się falą płaską.
Dla fali płaskiej rozchodzącej się w kierunku x równania Maxwella rozdzielają się na dwa niezaleŜna podukłady ( wykład):
(1)
(2)
E
∂
∂
H
∂
∂
y
H
y
E
z
= −µµ
z
= εε
x
o
∂
t
∂
∂ x
0
∂ t
∂ H
∂
∂ E
∂
= −
E
H
y
z
εε
=
y
z
µµ
0
∂ x
∂ t
0
∂ x
∂ t
E
H
x =
x = 0
0
H
Ex =
x = 0
0
Rozwiązaniami tych układów równań są niezaleŜne od siebie pary składowych ( Ey, Hz) dla podukładu (1) oraz ( Ez, Hy) dla podukładu (2). Fala elektromagnetyczna moŜe składać się z jednej lub drugiej pary pól. MoŜe teŜ zawierać obie pary w dowolnych proporcjach i z dowolną róŜnicą faz.
FALE MONOCHROMATYCZNE
Spośród wszystkich funkcji E(τ) największe znaczenie mają funkcje harmoniczne (sinωτ i cosωτ), poniewaŜ dowolną funkcję argumentu τ moŜemy przedstawić w postaci kombinacji funkcji harmonicznych (analiza Fouriera). Falę sinusoidalną o określonej częstości nazywamy falą monochromatyczną. NatęŜenie pola elektrycznego fali monochromatycznej moŜna przedstawić w postaci:
ω
E = E co
s
0
ω t − nr
v
gdzie ω = 2π / T jest częstotliwością lub częstością kołową fali. Wygodny jest zapis:
E = E cos
0
(ω t− kr)
ω
gdzie k =
n
k = ω εε µµ
nazywamy wektorem falowym. Długość wektora falowego,
.
v
0
0
~ iωτ
Funkcję A cos(ωτ) moŜna przedstawić jako część rzeczywistą funkcji wykładniczej Ae
~
A cos(
) = Re[
ωτ
ωτ
i
Ae
]
lub
~ iωτ
~
A cos ω
( τ )
1
= (
* − iωτ
Ae
+ A e
)
2
.
Najczęściej stosuje się zapis:
i (ω t− kr )
E = E e
+ .
c .
c
0
gdzie c.c. oznacza funkcję sprzęŜoną do funkcji stojącej przed znakiem dodawania.
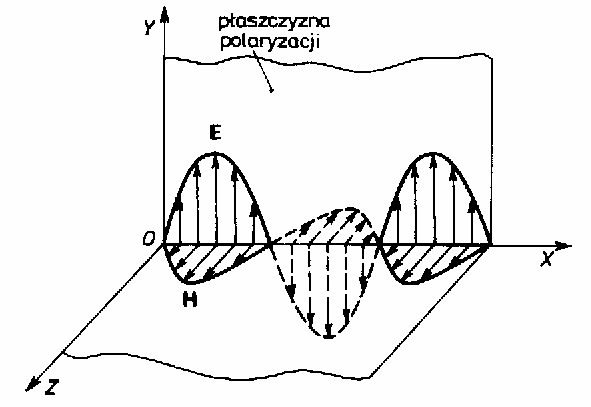
Fale elektromagnetyczne są falami poprzecznymi, co oznacza, Ŝe wektory E i H leŜą w płaszczyźnie prostopadłej do kierunku propagacji fali, czyli do kierunku wektora jej prędkości w danym punkcie
Fale elektromagnetyczne 23/
2
MONOCHROMATYCZNE FALE PŁASKIE
W kaŜdym punkcie pola elektromagnetycznego fali monochromatycznej rzuty wektorów E i
H na osie inercjalnego układu odniesienia wykonują drgania harmoniczne o jednakowej częstości.
1. O fali zawierającej tylko składowe ( Ey, Hz):
E = E co
t
ω − kx
y 0
(s
)
εε
0
H
=
E
z 0
y 0
H = H cos
t
ω − kx
µµ0
z 0
(
)
mówi się Ŝe jest spolaryzowana liniowo w kierunku osi y 2. O fali zawierającej tylko składowe ( Ez, Hy)
E = E co
t
ω − kx
z 0
(s
)
εε0
H
= −
E
y 0
z 0
H = H co
t
ω − kx
µµ
y 0
(s
)
0
mówi się Ŝe jest spolaryzowana liniowo w kierunku osi z Z równań Maxwella wynika ogólny związek między polem elektrycznym i polem magnetycznym fali:
εε
0
H =
n × E
µµ
0
1
lub, po podstawieniu B = εε H oraz v =
0
εε µµ
0
0
B = 1 n × E
v
Wynika z tego, Ŝe wzajemnie prostopadłe wektory E i H drgają w tej samej fazie, czyli jednocześnie osiągają wartości zerowe i maksymalne. Ich długości związane są zaleŜnością µµ H = εε E .
0
0
Znając pole elektryczne fali moŜemy jednoznacznie określić jej pole magnetyczne.
Fala spolaryzowana liniowo
Fale elektromagnetyczne 23/
3
POLARYZACJA FAL
W ogólnym przypadku pole elektryczne monochromatycznej fali płaskiej zawiera obie składowe mogące róŜnić się między sobą fazą początkową
E y = ˆ yA cos ω t − kx + δ
1
(
1 )
E z = ˆ zA cos ω t − kx + δ
2
(
2 )
δ1 - δ2 - przesunięcie fazowe
y
A1
E
z
A2
Wektor pola elektrycznego takiej fali zatacza elipsę a falę nazywa się spolaryzowaną eliptycznie.
W szczególnym przypadku, dla
• A1 = A2 i δ 1 - δ2 = (2 m + 1) π/2, m = 0, ±1, ... fala jest spolaryzowana kołowo.
• A1 = 0 lub A2 = 0 lub δ 1 - δ 2 = mπ fala jest spolaryzowana liniowo.
metody uzyskania fal spolaryzowanych (na przykład liniowo)
• emisja selektywna
• absorpcja selektywna
• selektywne odbicie
• dwójłomność
ENERGIA FALI ELEKTROMAGNETYCZNEJ
W kaŜdym punkcie, w którym istnieje pole elektryczne lub pole magnetyczne, jest zmagazynowana pewna energia. Gęstość energii fali elektromagnetycznej jest równa sumie gęstości energii pola elektrycznego i gęstości pola magnetycznego w danym punkcie: 1
e = e + e =
εε E 2 + µµ H 2
(
)
m
el
2
0
0
Po podstawieniu zaleŜności między wartościami E i H otrzymuje się 2
e = εε E
0
Z rozchodzeniem się fali elektromagnetycznej związany jest przepływ energii. Wektor gęstości strumienia energii, o wartości określającej ilość energii przepływającej w jednostce czasu przez powierzchnię jednostkową prostopadłą do kierunku propagacji, nazywany jest wektorem Poyntinga:
S = E × H
Fale elektromagnetyczne 23/
4
NatęŜeniem światła (natęŜeniem fali elektromagnetycznej) nazywa się średnią ilość energii jaką fala przenosi w jednostce czasu przez jednostkową powierzchnię prostopadłą do kierunku rozchodzenia się fali. NatęŜenie światła jest równe wartości średniej wektora Poyntinga w czasie jednego okresu drgań
T
1
I = S
=
∫ Sdt
ś r
T 0
Dla fali płaskiej spolaryzowanej liniowo
εε
S = EH =
0 E 2
µµ
0
dla t >> T
stąd zaleŜność między natęŜeniem światła a natęŜeniem pola elektrycznego fali elektromagnetycznej.
1
εε
2
0
I =
E 0
2
µµ0
Fale elektromagnetyczne 23/
5