3. Znają c transformację współrzę dnych Lorentza, dla
przypadku, gdy układ S2 porusza się wzglę dem S1 ze stałą
prę dkoś cią v wzdłuż osi x-ów:…wyprowadź transformację
prę dkoś ci. Przeanalizuj otrzymany wynik w porównaniu z
transformacją Galileusza.
Lorentzowskie dodawanie prędkości - transformacja
prędkości Lorentza
r
dr r
v =
Przypomnienie: Def. Prędkości:
dt (1.29)
składowe prędkości
vx = dx/dt
vy = dy/dt (1.30a-c)
vz = dz/dt
Korzystamy z TL wzór (1.21a-d) , następnie wyliczamy
różniczki kolejnych współrzędnych a potem ich pochodne po
czasie.
dx − vdt
( v − v) d t
1
1
1
1
dx
x
=
=
2
2
2
1 − ( v / c)
1 − ( v / c)
dy = dy
2
1
dz = dz
2
1 (1.31a-d)
2
2
dt − v / c dx
1
[ − ( v / c ) v ] dt
1
1
1
1
dt
x
=
=
2
2
2
1− ( v / c)
1− ( v / c)
Dzieląc obustronnie równania (1.31a-c) przez (1.31c)
otrzymujemy transformacje prędkości Lorentza w następującej
postaci:
v − v
1 x
v
=
2 x
1 − ( v / c 2 ) v 1 x
v
1 − v
( / c 2
)
1 y
v
=
2 y
1 − v
( / c 2 ) v 1 x (1.32a-c)
v
1 − ( v / c 2
)
1 z
v
=
2 z
1 − ( v / c 2 ) v 1 x
Ze związków (1.32a-d) wynika, że mimo iż ruch układu S2
względem S1 odbywa się wzdłuż osi x-ów to składowe
prędkości v2y oraz v2z zależą również od v1x. Dla v/c →0 TL
równania (1.32a-d) przechodzą w równania opisujące TG dla
prędkości.
v2x = v1x – v
v2y = v1y (1.33a-d) v2z = v1z
10. Dla równania ruchu: x=Asin(ω t+φ ) znajdź : prę dkość ,
przyspieszenie oraz wyraż enie na siłę , która powoduje taki
ruch. Objaś nij wielkoś ci wystę pują ce w równaniu ruchu.
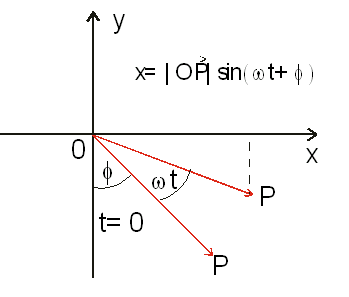
Korzystają c z wektora wirują cego podaj graficzną
interpretację wychylenia x w ruchu harmonicznym.
Wychylenie i siła
Szukamy wyrażenia na siłę, która powoduje ruch oscylacyjny
np. sinusoidalny.
x = A sin(ωt + ϕ) (2.18) gdzie:A – amplituda (maksymalne wychylenie dla sin (ωt+ϕ)
=1), ω = 2π/T (T okres ), jest prędkością kątową, ϕ - faza
początkowa ruchu (dla t=0)
Szukamy wyrażenia na prędkość v oraz na przyspieszenie a:
v = dx/dt = Aωcos(ωt + ϕ) (2.19) a = dv/dt = d2x/dt2 = - Aω2sin(ωt + ϕ) (2.20)
Znając wyrażenie na a możemy zapisać wzór na siłę F, która
musi działać na ciało, ażeby poruszało się ono ruchem
harmonicznym (np. sinusoidalnym). Zgodnie z zasadami
dynamiki Newtona otrzymujemy:
r
2
= r = − ω
F
ma
m
x (2.21)
F=-kx (2.22)
k jest stałą sprężystości zdefiniowaną :
k = mω2
(2.23)
Stąd relacja :
ω = (k/m)1/2 (2.24)
Wychylenie w ruchu harmonicznym można zilustrować za
pomocą wektora wirującego.
Wychylenie ciała w ruchu harmonicznym (sinusoidalnym)
można rozważyć, jako składową x-ową wektora OP, którego
moduł OP = A.
Wektor OP obraca się przeciwnie do ruchu wskazówek zegara
wokół osi O, z prędkością kątową ω i dla t=0, tworzy kąt ϕ z
osią y
Rys. Układ współrzędnych i wektor wirujący.
23. Podaj i zilustruj definicję zdolnoś ci rozdzielczej
Reyleigh’a.
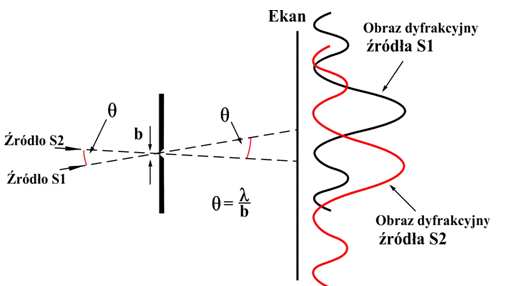
Zdolność rozdzielcza Reyleigh’a – iest to najmniejszy kąt jaki tworzą między sobą dwie fale pochodzące od dwóch
oddalonych źródeł, dla którego obrazy dyfrakcyjne mogą być
rozdzielone, przyjmuje się że dwa obrazy mogą być
rozdzielone, gdy centralne maksymum jednego (n>0) pokrywa
się z pierwszym minimum drugiego oznacza to, że θ=λ/b
32.Podaj prawa dla statycznych pól B i E. W oparciu o te
prawa omów własnoś ci tych pól.
Pola statyczne:Pola E i B traktowane oddzielnie, podstawowe
równanie pozwalające wyliczyć E i B, gdy znane są ładunki i
prądy
Prawo
Forma całkowa
Forma różniczkowa
Prawo Gaussa dla pola
r
ρ
r
r
q
divE =
E; pole źródłowe
∫ E ⋅ s
d =
Σ
ε
ε
Prawo Gaussa dla pola
r
∫ B ⋅ s
d
r
r
= 0
di B
v =
B; pole bez źródłowe
Σ
0
Krążenie pola E; pole
r
r
r
∫ E ⋅ dl = 0
ro E
t = 0
bez wirowe
Γ
Krążenie pola B; pole
r
r
∫ B ⋅ l
d = µ I
r
r
ro B
t = µ j
wirowe
0
Γ
0
33. Wylicz pole E oraz B w układzie wspolzednych S1 i S2
dla następującego przykładu: układ S2 porusza się względem
S1 z prędkością v (v,0,0) W układzie S2 znajdują się w
spoczynku ładunki Qi q. Ładunek Q znajduje się w początku
układu S2 i jest źródłem pola elektrycznego, ładunek q jest
ładunkiem próbnym. Rozważamy :
Układ S porusza się względem układu S wzdłuż osi x-ów 2
1
z prędkością v r . Ładunki q (ładunek próbny) oraz Q
ładunek, który wytwarza pole E ) znajdują się w spoczynku w układzie S . Ładunki q i Q są takie same w układzie 2
S i S .
1
2
Rys. 5.7 Układ współrzędnych oraz ładunki Q i q
W układzie S , występuje tylko oddziaływanie
2
elektryczne, którego siła jest opisana znanym wzorem (5.21).
r
r
F = qE
2
2
r
E jest polem elektrycznym wytworzonym przez ładunek
2
Q i mierzonym w punkcie, gdzie znajduje się ładunek q .
r
Składowe F są następujące: F
= qE
2
x 2
x 2
F
= qE F = qE
y 2
y 2
z 2
z 2
Obserwator znajdujący się w układzie S widzi ładunki Q
1
i q w ruchu, czyli występuje pole E i B , którego siła 1
1
wyraża się wzorem:
r
r
r
F = q( E + v r × B )
1
1
1
Po rozpisaniu iloczynu wektorowego i uwzględnieniu
składowej wektora v r ( v , 0 , 0 ) , otrzymujemy
następujące równania skalarne na składowe wektora siły w
r
układzie S : F ( F , F , F )
1
1
1
x
y 1
z 1
F
=
1
x
qE 1
x
F
=
q( E
− vB )
1
y
1
y
1
z
F
=
q( E
+ vB )
1
z
1
z
1
y
Zgodnie z transformacją Lorentza związki między siłą F w
1
układzie S , a siłą F w układzie S są następujące: 1
2
2
F
= F
x 2
1
x
F 1
y
F
=
F
y 2
1
=
2
F
z
z 2
v
2
1 −
v
1 −
2
c
2
c
Wykorzystując związki (5.22a-c) oraz (5.25a-c) otrzymujemy:
qE
=
x 2
qE 1
x
q( E
−
+
1
vB
y
1 )
z
q( E 1 vB
z
1 )
y
qE
=
=
y 2
qEz 2
2
v
2
v
1 −
1 −
2
c
2
c
Wzory (5.26a-c) stanowią TL dla pola elektromagnetycznego.
Wynika z nich, że pola E i B nie są wielkościami
rozdzielonymi, ale stanowią całość - pole elektromagnetyczne.
Rozdzielenie pola elektromagnetycznego na składową
elektryczną i magnetyczną nie jest sprawa bezwzględną, ale
zależy od ruchu ładunku w stosunku do obserwatora. Tak więc
możemy mówić o oddziaływaniach elektromagnetycznych.
Wyszukiwarka
Podobne podstrony:
egzamin fiz by qra
egzamin psi by?epfrez
ćw egzamin fiz
Egzamin 2k08 by Pepsi v1
zadania 2(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
EGZAMIN zerowy by Pepsi v0 11
zadania 9(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
materiały na egzamin, egzamin, opr by offca, METODY PRACY HODOWLANEJ - Pytania na egzamin:
zadania 7(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
Egzamin gleby?ited by 3
PYTANIA FIZJO EGZAMIN-seminarki gr.3, II ROK STOMATOLOGIA SUM ZABRZE, FIZJOLOGIA, FIZJOLOGIA EGZAMIN
egzamin fiz med 2012
sciaga egzamin III[1][1][1].1 by luke, aaa, studia 22.10.2014, całe sttudia, III semestr, teoria obw
zadania 5(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Teor
zadania 6(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 4(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
więcej podobnych podstron