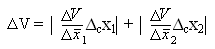Imię i Nazwisko:
Nr Zespołu:
Ocena Ostateczna
Grupa:
Tytuł ćwiczenia:
Nr ćwiczenia
Data Wykonania:
Prędkość dźwięku w powietrzu.
29
1. Wprowadzenie
Drgania harmoniczne, czyli ruch harmoniczny są to drgania opisane funkcją harmoniczną (sinusoidalną), jest to najprostszy w opisie matematycznym rodzaj drgań.
Ciało porusza się ruchem harmonicznym prostym, jeżeli znajduje się tylko pod wpływem siły o wartości proporcjonalnej do wychylenia z położenia równowagi i skierowanej w stronę położenia równowagi (prawo Hooke’a).
Fale podłużne – są to fale które drgają w tym samym kierunku.
Fale poprzeczne – maja kierunek drgań prostopadły do kierunku rozchodzenia się.
Superpozycja fal – to sumowanie się kilku niezależnych ruchów falowych.
Fala stojąca – fala, której pozycja w przestrzeni pozostaje niezmienna. Fala stojąca może zostać wytworzona w ośrodku poruszającym się względem obserwatora lub w przypadku interferencji dwóch fal poruszających się w przeciwnych kierunkach.
Fale rozchodzące się w powietrzu, które docierają do naszego ucha wywołują wrażenie dźwięku , mają częstotliwość f z przedziału od 16 do 20 000 Hz.
2. Metoda pomiaru
Pionowa rurka szklana, wypełniona częściowo wodą, połączona jest plastikową rurką ze zbiornikiem wody. Zbiornik można podnosić lub spuszczać za pomocą śruby, co prowadzi do zmiany poziomu wody w rurze, a tym samym wysokości słupa powietrza nad wodą. Wysokość słupa powietrza w rurze odczytujemy na skali milimetrowej. Nad rurą umocowany jest głośnik podłączony do generatora drgań. U
wylotu rury zamocowany jest mikrofon podłączony do oscyloskopu, na którym można obserwować sygnał z mikrofonu.
Lp
połorzenie x1 [cm] połorzenie x2 [cm]
1
15,4
53,3
2
15,5
53,4
3
15,1
53,6
4
15,4
53,3
5
15,3
53,6
x 1= 15,34 [cm]
x 2= 53,44 [cm]
f = 453,32 Hz
t = 25 oC
α=(1/273,15 °C)
- Obliczanie niepewności systematycznej:
∆sx = 0,05 [cm] = 0,0005 [m]
-
Obliczanie rozrzutu wartości x1 i x2:
x1max – x1min = 0,4 [cm] = 0,004 [m]
x2max – x2min = 0,3 [cm] = 0,003 [m]
rozrzut wartości jest znacznie większy od niepewności systematycznej, więc możemy pominąć niepewność systematyczną:
x1max – x1min >> ∆sx
x2max – x2min >> ∆sx
- Obliczanie niepewności przypadkowej (odchylenie standardowe średniej arytmetycznej):
S x 1= 0,068
S x 2= 0,068
ilość pomiarów jest mniejsza od dziesięciu, a więc odchylenie standardowe średniej arytmetycznej S x daje zaniżoną wartość niepewności systematycznej.
τ nα= 4,60 , gdzie n= 5, a α=0,99
∆cx1= S x . τ nα= 0,31
∆cx2= S x . τ nα= 0,31
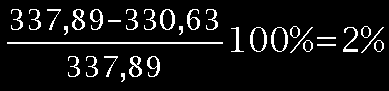
- Obliczanie długości fali w powietrzu:
λ = 2( x 2 - x 1) ≈ 76,2 [cm] = 0,762 [m]
- Obliczanie prędkość dźwięku w temperaturze pokojowej:
V = λ . f ≈ 345,43
- Obliczanie prędkości dźwięku w temperaturze 0°C
V0 = V / ( 1 + α t ) ≈ 330,63 [m/s]
- Obliczanie maksymalnej niepewności pomiaru:
∆V= 7,26 [m/s]
- Prędkość dźwięku w powietrzu w temperaturze 0°C:
V = ( 330,63 ± 7,26 ) [m/s]
V%=
4. Wnioski:
Wyniki prowadzonych obliczeń różnią się od wartości przedstawionych w tablicach , czego powodem są błędy pomiarowe i nie uwzględnienie wszystkich czynników jakie miały wpływ na dokładność pomiarów. Największy wpływ na obliczanie wartości V miał z pewnością pomiar związany z badaniem wysokości słupa powietrza w rurze.
Wyszukiwarka
Podobne podstrony:
ćw 29 sprawozdanie III
ćw. 29 sprawozdanie I
ETX16 20061012 Ćw[1] 29 sprawozdanie
więcej podobnych podstron