Materiały do zajęć: “Statystyka - ćwiczenia”
Testy istotności różnic dla k prób niezależnych
Omówione dotychczas metody służyły do porównywania dwóch grup niezależnych. Czasami jednak zależy nam na jednoczesnym porównaniu większej ilości grup. Teoretycznie można to przeprowadzić stosując na każdej możliwej do stworzenia parze grup testy omówione wcześniej.
Jest to jednak działanie nieekonomiczne (przy sześciu
porównywanych grupach wymaga przeprowadzenie aż 15 osobnych analiz) i, co więcej, metodologicznie niepoprawne, gdyż przyjęty poziom istotności z każdą kolejną analizą rośnie w sposób niekontrolowany (założone na wstępie a = 0,05 w kolejnych analizach jest w rzeczywistości co raz wyższe, można je wyliczyć ze wzoru 1-(1-a ) ) m .
W przypadkach, gdy mamy do czynienia z większą niż dwie liczbą porównywanych grup należy więc używać testów do tego przeznaczonych.
Aby wybrać odpowiedni test porównujący więcej niż dwie gupy należy rozpatrzeć następujące kryteria: a) skala pomiarowa zmiennej zależnej(testowanej)
jeśli skala jest ilościowa:
a) liczebności porównywanych prób
b) kształt rozkładu zmiennej w poszczególnych próbach (wartości skośności i kurtozy) c) homogeniczność wariancji rozkładów zmiennej zależnej
Poniższy Algorytm wyboru testu istotności różnicy dla k prób niezależnych może okazać się przydatny przy Rodzaj skali pomiarowej zmiennej zależnej
przedziałowa
porządkowa
nominalna
i ilorazowa
ocena
liczebności prób
równoliczne
nierównoliczne
ocena
normalności
rozkładu
TAK
NIE
ocena homoge-
niczności
wariancji
TAK
NIE
F
test H -
test chi2
test
analizy
Kruskala-Wallisa
wariancji
Rysunek 8.1.
Materiały do zajęć: “Statystyka - ćwiczenia”
Odpowiednikiem testu t-Studenta dla większej liczby porównywanych grup jest test F analizy wariancji - ANOVA (służy do porównywania więcej niż dwóch grup danych, przy zmiennej zależnej mierzonej na skali parametrycznej, przy równolicznych grupach o homogenicznych wariancjach, gdy rozkład zmiennej w porównywalnych próbach nie odbiega istotnie od normalnego). Test ten polega na porównaniu wariancji międzygrupowej z wariancją wewnątrzgrupową. To jest, im większe jest zróżnicowanie wyników pomiędzy porównywanymi grupami i mniejsze wewnątrz tych grup tym wyższą wartość testu F otrzymamy w wyniku analizy.
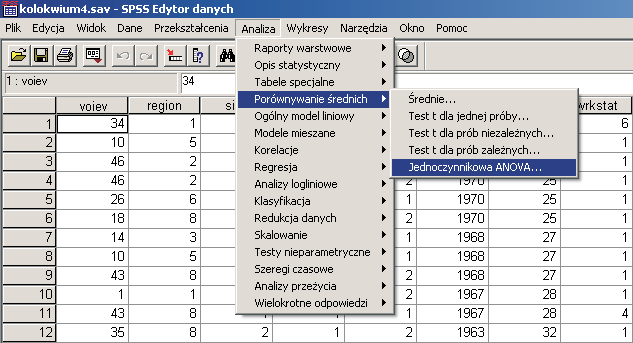
W SPSSie omawiana ANOVA znajduje się w menu “Analiza” w “Porównywanie średnich” pod nazwą
“Jednoczynnikowa ANOVA”.
Rysunek 8.2.
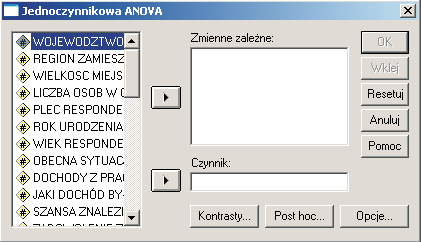
Po wybraniu tego polecenia pojawi się następujące okno:
Rysunek 8.3.

Materiały do zajęć: “Statystyka - ćwiczenia”
Podobnie jak w przypadku testu t-Studenta, w górnym oknie należy umieścić zmienną (zmienne) zależną a w dolnym zmienną grupującą (niezależną). Po wprowadzeniu odpowiednich danych należy nacisnąć klawisz “OK” lub “Wklej”.
Sam test F analizy wariancji ma tę wadę, że podaje tylko pojedynczy wynik, na podstawie którego można stwierdzić, czy któraś z porównywanych grup różni się istotnie od którejś innej. Nie można, niestety, na jego podstawie stwierdzić, między którymi grupami zachodzi istotna statystycznie różnica. W celu sprawdzenia istotności różnicy w poszczególnych parach grup należy użyć któregoś z testów kontrastów kryjących się pod klawiszem “Post Hoc”. Nie należy jednak liczyć kontrastów przed przeprowadzeniem samej analizy wariancji, ponieważ niektóre z nich bazują na teście t-Studenta i zawyżają prawdopodobieństwo. Zdarza się więc tak, że kontrast okazuje się istotny, chociaż wynik ANOVA nie jest istotny statystycznie. Dlatego jedynie wynik analizy wariancji dający podstawy do odrzucenia hipotezy zerowej, jest podstawą do podjęcia decyzji o użyciu testu kontrastów.
Poniżej znajduje się wydruk analizy wariancji testującej, czy w trzech grupach wykonujących zadanie w różnych warunkach (cisza, umiarkowany hałas i intensywny hałas) badani popełniali podobną liczbę błędów.
Rysunek 8.4.
Tak samo jak w przypadku wcześniej omówionych testów, na górze wydruku pojawia się nazwa obliczonego testu.
Poniżej, w tabeli podane są wartości sum kwadratów, stopni swobody oraz średnich kwadratów wewnątrzgrupowych i międzygrupowych. Na końcu wydruku pojawia się wartość testu F i jego istotność.
Na podstawie powyższych wyników można stwierdzić, że warunki w jakich pracowali badani nie miały istotnego wpływu na liczbę popełnianych przez nich błędów. Chcąc zacytować taki wynik należy zapisać: F(2,27)=0,117; p=0,890. Cytując wynik testu należy podać liczby stopni swobody zarówno między grupami jak i wewnątrz grup.
Interpretacja powyższego wyniku sprawadza się jedynie do oceny istotności wartości testu F - w tym wypadku jest nie istotna, więc postępowanie można zakończyć konkluzją o braku istotnych statystycznie różnic.
Sytuacja jest bardziej skomplikowana w przypadku uzyskania istotnej wartości testu F. Rozpatrzmy przykład z tego samego badania, dotyczący jednak porównania czasu potrzebnego na wykonanie zadania w zależności od warunków pracy.
Rysunek 8.5.
Na podstawie wyniku otrzymanego w przedstawionym powyżej przykładzie można stwierdzić, że istnieją istotne różnice między grupowe w zakresie czasu potrzebnego na wykonanie zadania uzależnione od warunków w jakich pracowali badani (F(2,27)=42,969; p<0,001). Oznacza to, że przynajmniej jedna z porównywanych grup (wyznacznych przez warunki wykonywania zadania) różni się istotnie pod względem czasu wykonywania zadania od przynajmniej jednej innej grupy. Aby jednak orzec jak, dokładnie, wyglądają różnice pomiędzy poszczególnymi grupami należy ponownie wybrać polecenie “jednoczynnikowa ANOVA” (patrz rys. 8.2) i w pojawiającym się oknie (patrz rys. 8.3) nacisnąć klawisz “Post Hoc”. Otworzy się wówczas następujące okno:

Materiały do zajęć: “Statystyka - ćwiczenia”
Rysunek 8.6.
W oknie tym pojawia się wybór wielu różnych testów służących do porównań par prób. Dla ułatwienia są one ułożone w kolejności od najmniej do najbardziej “wymagających”. To znaczy, pierwszy z testów - NIR daje wyniki takie jak wielokrotnie przeprowadzony test t-Studenta - czyli nadszacowuje istotność różnic, każdy kolejny wymaga większej różnicy między średnimi grupowymi by mogła być ona uznana za istotną. Dlatego warto czasem przeprowadzić kilka różnych testów kontrastów równolegle i porównać ich wyniki.
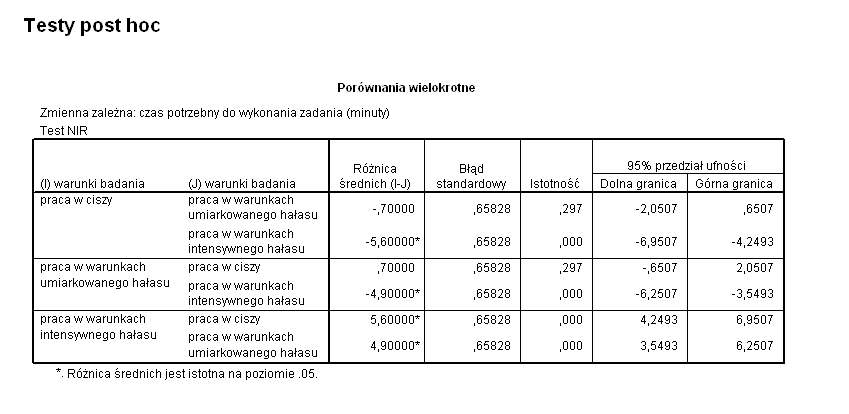
Najpowszechniej używany jest test NIR i jego wyniki możemy oglądać poniżej.
Wydruk prezentuje
zestawione w formie tabeli
pary grup
oraz podaje różnice średnich dla każdej pary grup.
Kluczową dla interpretacji wyników testu częścią wydruku jest kolumna zatytułowana “Istotność”. Analizując wartości z tej kolumny stwierdzimy, że istotne różnice występują między grupami “praca w ciszy” i “praca w warunkach intensywnego hałasu” (p<0,001) oraz miedzy grupami “praca w warunkach umiarkowanego hałasu” i “praca w warunkach intensywnego hałasu” (p<0,001). Grupy “praca w ciszy” i “praca w warunkach umiarkowanego hałasu” nie różnią się istotnie pod względem czasu potrzebnego do wykonania zadania (p=0,297).

Materiały do zajęć: “Statystyka - ćwiczenia”
Testowanie założeń do ANOVA
Jak wspomniano na wstępie, ANOVA wymaga, by analizowana dane spełniały szereg wymogów. Po pierwsze, zmienna analizowana w grupach powinna być zmienną ilościową. Po drugie liczebność porównywanych prób powinna być jednakowa. Można ją sprawdzić używając polecenia “Częstości” z menu “Analiza”, “Opis statystyczny” (patrz rys 4.1). Po trzecie, rozkład zmiennej zależnej w porównywanych grupach nie powinien istotnie odbiegać od rozkładu normalnego. Można to sprawdzić obliczając skośność i kurtozę, używając polecenia “Eksploracja” z menu “Analiza”,
“Opis statystyczny” (patrz rys. 5.7). Zarówno wartość skośności, jak i kurtozy powinny mieścić się w przedziale (-1;1).
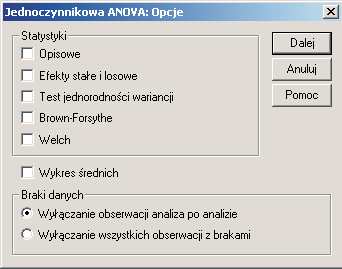
Po czwarte wariancje w porównywanych grupach powinny być homogeniczne, co można sprawdzić za pomocą testu jednorodności wariancji Levene’a. Oblicz się go wybierając w oknie jednoczynnikowej ANOVAy klawisz “Opcje” (patrz rys. 8.3). Pojawi się wówczas następujące okno:
Rysunek 8.8.
W ramce statystyki należy zaznaczyć “Test jednorodności wariancji”.
Wydruk analizy wariancji zostanie poprzedzony wynikami testu jednorodności wariancji Lavene’a. Nieistotny wynik tego testu upoważnia do stosowania ANOVAy. Wynik istotny wskazuje na istotne różnice wariancji w poszczególnych próbach.
Wynik testu Levene’a dla analizowanego wcześniej przykładu wpływu warunków badania na czas wykonywania zadania znajduje się poniżej.
Rysunek 8.9.
Jak widać powyżej istotność testu Lavene’a jest wyższa niż p< 0,05, nie ma więc podstaw, by twierdzić, że wariancje w badanych próbach różnią się istotnie.
W przypadku, gdy zmienna zależna mierzona jest na skali porządkowej, lub gdy nie są spełnione założenia ANOVA można porównywać badane próby za pomocą nieparametrycznego odpowiednika analizy wariancji - testu H-Kruskala-Walisa. Znajduje on zastosowanie w warunkach badawczych podobnych do tych, w których znajduje zastosowanie test U-Manna-Whitneya, z tą tylko różnicą, że przeznaczony jest on do testowanie hipotezy zerowej dotyczącej większej ilości porównywanych grup.
W SPSSie testu tego należy szukać w menu “Analiza”, “Testy nieparametryczne” pod hasłem “K prób niezależnych”.
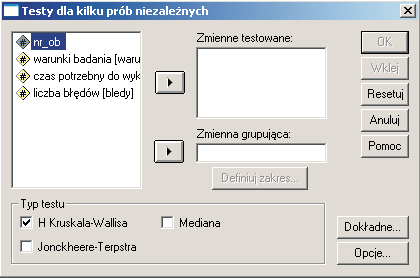
Materiały do zajęć: “Statystyka - ćwiczenia”
Rysunek 8.10.
Pojawi się wówczas natępujące okno.
Rysunek 8.11.
Zmienne wprowadza się do analizy analogicznie jak w przypadku analizy wariancji - w górnym oknie powinna się znaleźć zmienna porównywana w grupach a w dolnym ta, która dzieli badanych na kategorie. Po wprowadzeniu zmiennej grupującej należy nacisnąć przycisk “Definiuj zakres” i podać wartości przypisane skrajnym z porównywanych prób. Po wprowadzeniu wszystkich pożądanych zmiennych należy wcisnąć “OK” lub “Wklej”.
W oknie raportów pojawi się następujący wydruk:
Materiały do zajęć: “Statystyka - ćwiczenia”
Rysunek 8.12.
Na wydruku pojawia się, jak zwykle, nazwa przeprowadzonej analizy. Poniżej, tak jak w teście U-Manna-Whitneya, pojawiają się średnie rangi oraz liczebności dla poszczególnych grup. Wydruk kończy się wartością chi2 (H ma rozkład zbliżony do chi )
2
oraz jej istotnością.
Jak widać w naszym przykładzie różnica między grupami okazuje się być nieistotna statystycznie (chi (2)=3,146; 2
p=0,207). Gdyby była istotna, to, podobnie jak w przypadku analizy wariancji, nie moglibyśmy na podstawie otrzymanego wyniku orzec, które grupy różnią się od których. Test H-Kruskala-Wallisa nie posiada, niestety, testów
“post hoc”. Jedyną więc metodą dogłębniejszego zbadania otrzymanych danych jest przeprowadzenie na każdej parze testu U-Manna-Whitneya. Należy jednak pamiętać jakim błędem obciążone są takie wyniki.
W przypadku, gdy zmienna, którą porównujemy w grupach jest zmienną nominalną używamy testu chi , 2
który był już
omówiony wraz z metodami służącymi do porównywania dwóch prób niezależnych.
Wyszukiwarka
Podobne podstrony:
Opis analizowanych wariantów inwestycji
Jednoczynnikowa analiza wariancji
Analiza wariancji wprowadzenie
Analiza wariancji
Hierarchiczna analiza wariancji zadania Word2003, Elementy matematyki wyższej
więcej podobnych podstron