A

B

D

F

A

F

B

A

F

B

C

D

C

D

A

E

C

D

E

E

D

F

F

A

B

E

G

r

a

f

i

j

e

g

o

r

e

p

r

e

z

e

n

t

a

c

j

a

w

p

o

s

t

a

c

i

l

i

s

t

y

s

ą

s

i

e

d

z

t

w

.

C

y

k

l

E

u

l

e

r

a

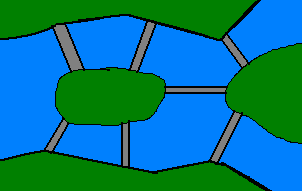
Zamknięta ścieżka zawierająca każdą krawędź grafu

(w rzeczywistości to nie jest cykl, bo cykl jest drogą – ma różne wierzchołki – cykl Eulera może nie mieć różnych wierzchołków) Mosty w Królewcu

Zadanie:

- narysować graf bez odrywania ołówka od papieru i nie rysując tej samej krawędzi wiele razy oraz wracając do punktu wyjścia Tw. Eulera (1736)

Graf spójny G jest grafem eulerowskim wtedy i tylko wtedy, gdy stopień każdego wierzchołka grafu G jest liczbą parzystą.

Graf spójny G jest grafem półeulerowskim wtedy i tylko wtedy, gdy ma dokładnie dwa wierzchołki nieparzystego stopnia.

A

A

B

C

B

C

B

C

D

E

D

E

D

E

F

Graf eulerowski Graf półeulerowski Graf nie eulerowski

l

g

o

r

y

t

m

F

l

e

u

r

y

’

e

g

o

k

o

n

s

t

r

u

k

c

j

i

c

y

k

l

u

E

u

l

e

r

a

w

g

r

a

f

i

e

A

s

p

ó

j

n

y

m

:

Zacznij cykl w dowolnym wierzchołku i przechodź krawędzie w dowolnej kolejności, ale zgodnie z zasadami:

a) usuwaj z grafu przechodzone krawędzie i wierzchołki

izolowane powstające w wyniku usuwania tych krawędzi,

b) w dowolnym momencie przechodź przez most tylko wtedy, gdy nie masz innego wyjścia.

A

A

A

A

A

B

C

B

C

B

C

B

C

B

C

D

E

D

E

D

E

D

E

D

E

F

F

F

F

A

A

A

A

A

B

C

B

C

B

C

C

D

E

E

D

z

i

a

ł

a

n

i

e

a

l

g

o

r

y

t

m

u

F

l

e

u

r

y

’

e

g

o

d

l

a

p

r

z

y

k

ł

a

d

o

w

e

g

o

g

r

a

f

u

e

u

l

e

r

o

w

s

k

i

e

g

o

.

A

A

A

A

A

B

C

B

C

B

C

B

C

B

C

D

E

D

E

D

E

D

E

D

E

F

F

F

F

F

A

A

A

A

A

B

C

B

C

B

C

B

C

B

C

D

E

D

E

D

E

D

E

D

E

F

F

F

F

F

r

z

e

w

o

:

D

1

.

Spójny las.

2

.

Hierarchia węzłów z warunkami:

a) najwyższy poziom w hierarchii zajmuje tylko jeden węzeł

(korzeń).

b) wszystkie węzły z wyjątkiem korzenia są powiązane z

jednym i tylko jednym węzłem znajdującym się na wyższym

niż one poziomie.

3

n

u

t

h

)

.

(

D

.

K

Skończony zbiór T złożony z jednego lub wielu węzłów

spełniający warunki:

a) Istnieje wyróżniony węzeł zwany korzeniem.

b) Pozostałe węzły są podzielone na m >= 0 parami rozłącznych zbiorów T1, ..., Tm, z których każdy jest drzewem. Zbiory te są poddrzewami danego drzewa.

i

n

i

m

a

l

n

e

d

r

z

e

w

o

r

o

z

p

i

n

a

j

ą

c

e

s

p

i

n

a

j

ą

c

e

)

M

(

Dane:

- graf etykietowany (ważony) kosztem przejścia między

węzłami

Zadanie:

- znaleźć minimalne drzewo rozpinające:

• dociera dokładnie do każdego węzła grafu

• jest najtańszym z takich drzew (minimalizuje sumę wag na krawędziach)

• (takich drzew może być wiele)

Algorytmy:

1. Prima – dołączanie najtańszych, bezpiecznych krawędzi do istniejącego drzewa

2. Kruskala – analiza najtańszych, bezpiecznych krawędzi tworząc las, który w końcu połączy się w drzewo

- krawędź bezpieczna – taka krawędź, której dołączenie do drzewa nie spowoduje powstania cyklu (drzewo musi być

grafem acyklicznym)

- algorytm zachłanny – algorytm wybierający kolejno krawędzie o najmniejszej wadze

KROK 2 : U={A,C}, V-U={B,D,E,F}

KROK 1 : V={A,B,C,D,E,F},

A

Najta sza kraw d (C,F) =4

U={A}, V-U={B,C,D,E,F}

ń

ę

ź

A

Najta sza kraw d (A,C) =1

ń

ę

ź

6

6

5

5

1

1

B

5

5

D

B

5

5

D

C

C

3

3

6

4

2

6

4

2

E

F

E

F

6

6

A

A

KROK 3 : U={A,C,F}, V-U={B,D,E}

KROK 4 : U={A,C,F,D}, V-U={B,E}

Najta sza kraw d (F,D) =2

ń

ę

ź

Najta sza kraw d (C,B) =5

ń

ę

ź

6

6

5

5

1

1

B

5

5

D

B

5

5

D

C

C

3

3

6

4

2

6

4

2

E

F

E

F

6

6

KROK 5 : U={A,C,F,D,B}, V-U={E}

KROK 6 : U={A,C,F,D,B,E} = V

A

A

Najta sza kraw d (B,E) =3

KONIEC ALGORYTMU PRIMA

ń

ę

ź

6

6

5

5

1

1

B

5

5

D

B

5

5

D

C

C

3

3

6

4

2

6

4

2

E

F

E

F

6

6

Przykład realizacji algorytmu Prima.

KROK 1 : V={A,B,C,D,E,F},

T=(V,E) gdzie E={Ø}, Najta sza kraw d (A,C) =1

KROK 2 : E={(A,C)}

ń

ę

ź

A

Najta sza kraw d (F,D) =2

ń

ę

ź

A

6

6

5

5

1

1

B

5

5

D

B

5

5

C

C

3

3

6

4

2

6

4

2

E

F

E

F

6

6

A

KROK 4

A

KROK 3

: E= {(A,C),(F,D),(B,E)}

: E={(A,C),(F,D)}

Najta sza kraw d (C,F) =4

Najta sza kraw d (B,E) =3

ń

ę

ź

ń

ę

ź

6

6

5

5

1

1

B

5

5

D

B

5

5

D

C

C

3

3

6

4

2

6

4

2

E

F

E

F

6

6

KROK 5 : E= {(A,C),(F,D),(B,E),(C,F)}

KROK 6 : E= {(A,C),(F,D),(B,E),(C,F),(B,C)}

Ź

Najta sza kraw d (B,C) =5

A

A

KOLEJNA KRAW D UTWORZYŁABY CYKL

Ę

ń

ę

ź

KONIEC ALGORYTMU KRUSKALA

6

6

5

5

1

1

B

5

5

D

B

5

5

D

C

C

3

3

6

4

2

6

4

2

E

F

E

F

6

6

Przykład realizacji algorytmu Kruskala.

.

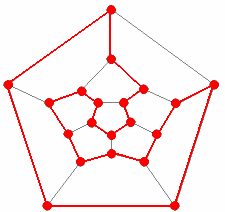
Graf dwunastościanu. Na czerwono zaznaczono cykl Hamiltona