Wstęp
1.1
Statystyka zajmuje się opisywaniem i analizą zjawisk masowych, badniem prawidłowości występujących w zbiorowościach elementów zróżnicowanych ze względu na badane cechy (populacjach statystycznych).
Badania statystyczne dzielą się na
• badania pełne
• badania częściowe.
Wyróżniamy:
• statystykę opisowa
• statystykę matematyczną
Statystyka matematyczna pozwala wyciągać wnioski dotyczące badanej cechy w całej populacji na podstawie wyników badania próbnego. Wnioskowanie powyższe jest możliwe dzięki użyciu metod i narzędzi rachunku prawdopodobieństwa.
Badanie statystyczne: obserwujemy wartości pewnej cechy dla wybranych elementów populacji i na tej podstawie chcemy odpowiedzieć na jedno z pytań, dotyczących konkretnego parametru tej cechy (na przykład jej wartości średniej). Typowe problemy, które dają się rozwiązać metodami wnioskowania statystycznego.
1. Ile wynosi parametr (na przykład średnia) naszej cechy w całej populacji? Estymacja punktowa 2. W jakim zakresie (zbiorze) znajduje się ten parametr? Estymacja przedziałowa 3. Czy prawdą jest, że nasz parametr należy do określonego zbioru? Testowanie hipotez statystycznych Populacją nazywamy zbiór (skończony lub nieskończony) elementów podlegających badaniu ze względu na jedną albo wiele cech.
Z populacji pobieramy do badania próbę statystyczną, skończony podzbiór populacji, którego elementy losujemy.
Losowość próby oznacza, że jej wyniki możemy traktować jako realizacje zmiennych losowych o rozkładzie identycznym z rozkladem badanej cechy.
Różne schematy losowania:
• losowania niezależne (ze zwracaniem) i zależne (bez zwracania)
• losowania indywidualne i zespołowe
• losowania jednostopniowe i wileostopniowe
• losowania nieograniczone i ograniczone
Próbą prostą wylosowaną z pewnej ustalonej populacji nazywa się taką próbę losową, której wyniki są niezależnymi zmiennymi losowymi o jednakowych rozkładach identycznych z rozkładem badanej cechy.
X - badana cecha - zmienna losowa
(X1, . . . , Xn) - n-elementowa próba prosta - wektor losowy (x1, . . . , xn) - wyniki badania (dane) - realizacja wektora losowego Każdą funkcję g(X1, . . . , Xn) będącą funkcją próby losowej nazywamy statystyką.
Przykłady statystyk:
n
n
n
¯
1 X
1 X
1
X
X =
Xi, ¯
S2 =
(Xi − ¯
X)2, S2 =
(Xi − ¯
X)2.
n
n
n − 1
i=1
i=1
i=1
Ich realizacje:
n
n
n
1 X
1 X
1
X
¯
x =
xi, ¯
s2 =
(xi − ¯
x)2, s2 =
(xi − ¯
x)2.
n
n
n − 1
i=1
i=1
i=1
Przykład 1 Badano czas pracy baterii pewnego typu. Z populacji baterii pobrano próbę 50-elementową i otrzymano następujące wyniki:
1


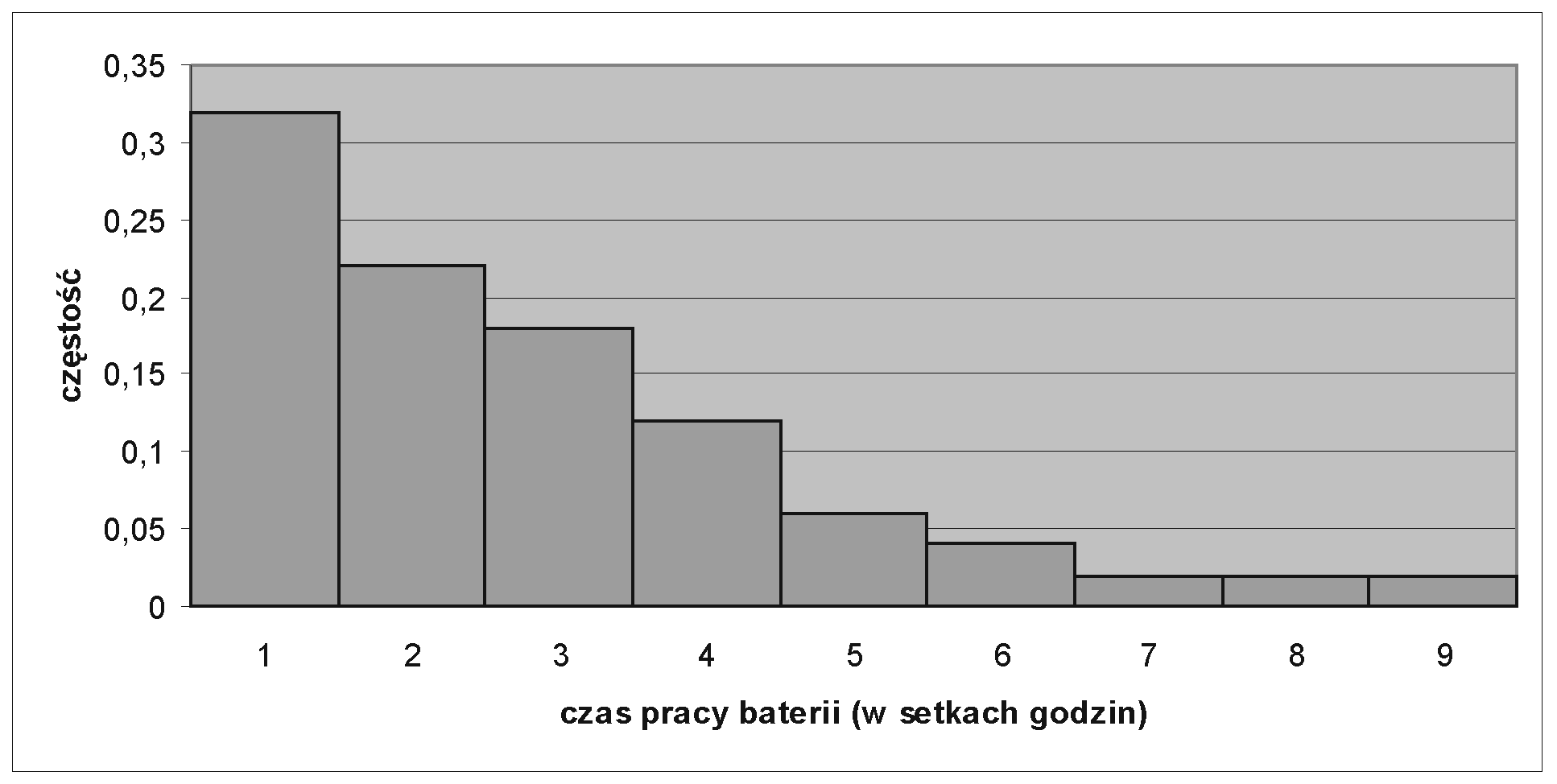
Histogram
Przy dużych próbach wartości grupuje się w klasach, najczęściej jednakowej długości, przyjmując założenie, że wszystkie wartości w danej klasie są identyczne ze środkiem klasy ¯
xi, i = 1, . . . , k.
Metody ustalania liczby klas:
liczba klas k
liczba pomiarów
30-60
6-8
60-100
7-10
√
k =
n
k ≤ 5 ln n.
100-200
9-12
200-500
11-17
500-1500
16-25
Liczbę wartości należących do i-tej klasy nazywamy licznością i-tej klasy, ni.
k
X ni = n.
i=1
Ciąg par (¯
xi, ni)i=1,...,k nazywamy szeregiem rozdzielczym.
2
Parametry empiryczne
Definicja Średnią arytmetyczną nazywamy statystykę
n
¯
1 X
X =
Xi.
n i=1
Miara tendencji centralnej.
Realizację staystyki ¯
X obliczamy z próby.
W przykładzie z bateriami
n
1 X
1
¯
x =
xi =
· 113, 32 = 2, 26648.
50
50
i=1
Dla szeregu rozdzielczego (średnia ważona):
k
1 X
¯
x =
ni ¯
xi.
n i=1
W przykładzie z bateriami
¯
xi
0,48
1,47
2,55
3,40
4,43
5,34
6,43
7,54
8,22
ni
0,32
0,22
0,18
0,12
0,06
0,04
0,02
0,02
0,02
n
k
1 X
¯
x =
ni ¯
xi = 2, 27
50 i=1
Inną miarą tendencji centralnej jest tak zwana mediana. Dla danego ciągu liczb x1, . . . , xn, określamy ciąg x(1), . . . , x(n), który powstaje przez jego niemalejące uporządkowanie, czyli: x(1) ≤ x(2) ≤ · · · ≤ x(n).
Definicja Medianą cechy X, przyjmującej wartości x1, . . . , xn, nazywamy środkowy wyraz ciągu x(1), . . . , x(n), gdy n jest liczbą nieparzystą, lub średnią arytmetyczną dwóch wyrazów środkowych, gdy n jest liczbą parzystą, (
x(k+1)
dla
n = 2k + 1
me =
x(k)+x(k+1)
dla
n = 2k.
2
W przykładzie z bateriami
1
1
me =
(x25 + x26) =
(1, 725 + 1, 702) = 1, 7135
2
2
Przykład
Wskazać miary tendencji centralnej wynagrodzeń pracowniczych, na podstawie poniższej listy płac pewnego zakładu liczącego dziesięciu pracowników:
1
850 zł
6
1080 zł
2
870 zł
7
1090 zł
3
950 zł
8
2700 zł
4
1000 zł
9
2900 zł
5
1050 zł
10
7200 zł
Średnia:
850 + 870 + . . . + 2900 + 7200
¯
x =
= 1969 zł.
10
Mediana:
1050 + 1080
me =
= 1065 zł.
2
Jak widać, w naszym przykładzie wartość średnia różni się znacznie od mediany. Wyobraźmy sobie sytuację, że osoby o niskich pensjach w przedstawionej firmie będą dążyć do uzyskania podwyżki. Poinformują na pewno, że średni zarobek w firmie to tylko 1065 złotych. Osoby lepiej zarabiające będą opierały się na innych obliczeniach i stwierdzą, że zarobki są wysokie i wynoszą średnio 1969 złotych. I kto mówi prawdę? Jedni i drudzy.
Miary rozproszenia
3
R = Xmax − Xmin.
Definicja Wariancja z próby
n
1 X
S2 =
(Xi − ¯
X)2
n i=1
n
n
1
X
S2
∗ =
S2 =
(Xi − ¯
X)2
n − 1
n − 1 i=1
Jeśli znamy wartość oczekiwaną m cechy X, to
n
1 X
S2 =
(X
0
i − m)2
n i=1
Równoważne wzory:
n
n
1 X
1 X
S2 =
X2 − ¯
X2 =
(Xi − a)2 − ( ¯
X − a)2
n
i
n
i=1
i=1
dla dowolnego a ∈ R.
Dla szeregu rozdzielczego:
k
1 X
s2 =
(¯
xi − ¯
x)2ni
n i=1
W przykładzie z bateriami
s2 = 3, 67,
s2∗ = 3, 74,
s = 1, 935.
Inne parametry:
• odchylenie standardowe
√
S =
S2
• odchylenie od wartości średniej
n
1 X
b =
|Xi − ¯
X|
n i=1
• moment centralny rzędu k
n
1 X
Mk =
(Xi − ¯
X)k
n i=1
• współczynnik asymetrii
M3
S3
• współczynnik koncentracji
M4 − 3
S4
3
Estymacja punktowa
Załóżmy, że rozkład badanej cechy X zależy od nieznanego parametru θ. Będziemy szacować θ w oparciu o n-elementową próbę prostą (X1, . . . , Xn).
Otrzymaną na podstawie konkretnej realizacji próby wartość nazywamy oceną (oszacowaniem) parametru θ. Każdą statystykę, której wartościami są oceny parametru θ nazywamy estymatorem parametru θ i oznaczamy parametru ¯
θ.
Na przykład
n
¯
1 X
X =
Xi
n i=1
jest estymatorem parametru EX.
4
x = 2, 266.
Jeśli przyjąć, że cecha X ma rozkład wykładniczy z parametrem λ = 1 , to
= 2.
2
EX = 1
λ
Dla danego parametru można utworzyć wiele estymatorów. Powstaje więc problem, jaki estymator należy stosować w konkretnej sytuacji. Rozwiązuje się go w ten sposób, że wprowadza się kilka kryteriów, które powinien spełniać ”dobryestymator,
,
a następnie bada się, czy rozpatrywany przez nas estymator spełnia te kryteria. Istnieją też sposoby porównywania między sobą estymatorów tego samego parametru.
W dalszej części podajemy dwa kryteria oceny jakości estymatorów parametrów liczbowych.
Niech (X1, . . . , Xn) będzie próbką prostą z populacji, w której badana jest cecha X.
Definicja Estymator ˆ
θ nazywamy estymatorem zgodnym parametru θ, jeżeli
ˆ P
θ −→ θ.
ˆ P
θ −→ θ ⇐⇒ ∀ε > 0 lim P (|ˆ
θ − θ| ≥ ε) = 0
n→∞
Przykład Średnia ¯
X jest estymatorem zgodnym wartości oczekiwanej.
Wniosek ze słabego prawa wielkich liczb.
Niech (X1, . . . , Xn) będzie próbką prostą z populacji, w której badana jest cecha X.
Definicja Estymator ˆ
θ nazywamy estymatorem nieobciążonym parametru θ, jeżeli Êθ = θ.
Estymator, który nie jest nieobciążony nazywamy estymatorem obciążonym.
Przykład Średnia arytmetyczna jest estymatorem nieobciążonym wartości oczekiwanej EX.
Rzeczywiście,
X
1 + · · · + Xn
1
E( ¯
Xn) = E
=
E(X1 + · · · + Xn)
n
n
1
=
nE(X) = E(X).
n
Przykład Statystyka S2 jest nieobciążonym estymatorem wariancji 2X.
0
D
Rzeczywiście,
n
!
n
1 X
1 X
ES2 =
(X
=
0
E
i − m)2
E((Xi − m)2)
n
n
i=1
i=1
1
=
n 2
2
D (X) = D X.
n
Przykład Statystyka S2 jest obciążonym estymatorem wariancji 2
D X.
n
1 X
1
E(S2) = E
(Xi − ¯
X)2 =
nE((X1 − ¯
X)2)
n
n
i=1
X
2 !
1 + · · · + Xn
= E
X1 −
n
n − 1
X
2 !
2 + · · · + Xn
= E
X1 −
n
n
n − 1
(X
2 !
2 − m) + · · · + (Xn − m)
= E
(X1 − m) −
n
n
n − 1
(X
2 !
2 − m) + · · · + (Xn − m)
E(S2) = E
(X1 − m) −
n
n
1
=
(n − 1)2E((X1 − m)2) + E((X2 − m)2) + . . .
n2
1
+E((X
2
2
n − m)2) =
(n − 1)2D (X) + (n − 1)D (X)
n2
1
n − 1
=
(n − 1)(n − 1 + 1) 2
2
D (X) =
D (X).
n2
n
5
Mimo, że estymator S2 jest obciążony, jest on często używany, gdyż dla dużej próbki n − 1 ≈ 1.
n
Inaczej mówiąc, obciążenie tego estymatora jest dla dużych n nieistotne. Estymatory o takiej własności nazywa się estymatorami asymptotycznie nieobciążonymi.
Przykład Statystyka S2
2
∗ jest obciążonym estymatorem wariancji D X .
n
2
E(S2
∗ ) =
E(S2) = D (X).
n − 1
4
MNW
Jedna z najczęściej stosowanych metod estymacji punktowej - metoda największejwiarygodności.
Przykład
Spośród studentów informatyki pewnego elitarnego wydziału wybrano losowo i niezależnie od siebie 50 osób, a następnie każdą z nich spytano, czy kiedykolwiek w trakcie studiów otrzymała ocenę niedostateczną. Okazało się, iż 14 osób odpowiedziało ”TAK”, natomiast pozostałe odpowiedziały “NIE”. Pytamy teraz: jaki procent studentów informatyki otrzymał w trakcie swoich studiów ocenę niedostateczną.
Mamy tutaj zaobserwowaną próbkę prostą (x1, . . . , xn, n = 50, z rozkładu dwupunktowego: 0 interpretujemy jako “NIE”, zaś 1 - jako ”TAK”. Naszym zadaniem jest wskazanie parametru p. Oczywiście, nie potrafimy tego zrobić dokładnie na podstawie samej tylko próbki, natomiast możemy możliwie najlepiej przybliżyć jego nieznaną wartość w następujący sposób: obliczamy prawdopodobieństwo wylosowania naszej próbki w zależności od p, a następnie uznajemy, że najlepszym przybliżeniem nieznanego parametru będzie taka wartość p, dla której obliczone właśnie prawdopodobieństwo jest największe.
Korzystając z niezależności zmiennych losowych X1, . . . , Xn otrzymujemy: P (X1 = x1, . . . , Xn = xn) = P (X1 = x1) · · · · · P (Xn = xn).
Zauważmy, że:
p,
gdy x
P (X
i = 1
i = xi) =
1 − p,
gdy xi = 0.
Z treści zadania wiemy, że xi = 1 dla dokładnie 14 wartości i .
P (X1 = x1, . . . , Xn = xn) = p14(1 − p)36.
Pozostaje nam wyznaczyć największą wartość funkcji l : [0, 1] −→ R, zadanej wzorem: l(p) = p14(1 − p)36
funkcja (największej) wiarygodności.
W celu wyznaczenia ˆ
p wykorzystamy powszechnie używaną metodę upraszczającą obliczenia - rozważymy mianowicie funkcję
L(p) = ln l(p),
która przyjmuje wartość największą dokładnie w tych samych punktach, co funkcja l.
L(p) = 14 ln p + 36 ln(1 − p).
14
36
L0(p) =
−
,
p
1 − p
14
36
L0(p) = 0,
−
= 0,
p
1 − p
14
ˆ
p =
= 0, 28.
50
Otrzymany w ten sposób estymator nazywa się estymatorem największej wiarygodności parametru p.
Metoda największej wiarygodności polega więc na skonstruowaniu funkcji wiarygodności odpowiadającej zaobserwo-wanemu zdarzeniu, zależnej od szukanych (estymowanych) parametrów, a następnie na znalezieniu takich wartości tych parametrów, dla których funkcja ta osiąga największą wartość.
6
• Jeśli zmienna losowa X ma rozkład dyskretny, P (X = w) = p(w, θ1, . . . , θk), to l(θ1, . . . , θk) = p(x1, θ1, . . . , θk) · . . . · p(xn, θ1, . . . , θk).
• Jeśli zmienna losowa X ma rozkład absolutnie ciągły gęstości f , zależnej od parametrów θ1, . . . , θk, R 3 x → f (x, θ1, . . . , θk) ∈ [0, ∞),
to
l(θ1, . . . , θk) = f (x1, θ1, . . . , θk) · . . . · f (xn, θ1, . . . , θk).
Przykład
Rozważmy próbkę prostą (X1, . . . , Xn) z rozkładu wykładniczego X o parametrze λ > 0. Znajdziemy estymator największej wiarygodności dla tego parametru.
0
dla x < 0
f (x) =
λe−λx
dla x ≥ 0.
Funkcja wiarygodności:
l(λ) = λe−λx1 · . . . · λe−λxn = λne−λ Pn x
i=1
i = λne−λn¯
x
L(λ) = ln l(λ) = n ln λ − λn¯
x.
n
L0(λ) =
− n¯
x
λ
1
L0(λ) = 0 ⇐⇒ ˆ
λ =
,
¯
x
który jest właśnie szukanym estymatorem parametru λ.
7
Wyszukiwarka
Podobne podstrony:
notatki z wykładów od J Pudełko, statystyka nota1
notatki z wykladow od J Pudelko Nieznany
GLEBOZNAWSTWO wykłady od 3 6 notatka
Notatka o przestepstwie z wykladow od Angeli, Studia PO i PR, prawo rodzinne i opiekuńcze
egzamin wykłady od sylwii, sggw, semestr III, statystyka
ZAGADNIENIA do egzaminu 2009 MARKETING, zootechnika UPH Siedlce, 4 rok 1 semest, Notatki, Marketing
Wsbif-Wyklad4-Statystyka, notatki ze studiów rok1, statystyka
Wsbif-Wyklad2-Statystyka, notatki ze studiów rok1, statystyka
Wsbif-Wyklad6-Statystyka, notatki ze studiów rok1, statystyka
zachomikowane notatki i wyklady, Estetyka - przedmiot nauki, Estetyka jako nauka funkcjonuje od XVII
notatki z wykładów statystyka informa marketing, zarządzanie i inżynieria produkcji
Finanse zaległe od Ewy, Finanse i rachunkowość UMK notatki wykłady pytania egzaminy, II część, Finan
Wsbif-Wyklad7-Statystyka, notatki ze studiów rok1, statystyka
Wsbif-Wyklad1-Statystyka, notatki ze studiów rok1, statystyka
testystata5, Finanse i rachunkowość UMK notatki wykłady pytania egzaminy, II część, Statystyka, Stat
Wsbif-Wyklad5-Statystyka, notatki ze studiów rok1, statystyka
Wykład 2 od profesora Biniaka
Prawo cywilne notatki z wykładów prof Ziemianin
prof łaszczyca przwo administracyjne notatki z wykładów5
więcej podobnych podstron
