1.Część Teoretyczna

siatke dyfrakcyjną stanowi szereg szczelin umieszczonych w równych od siebie odległościach na nieprzeźroczystym ekranie. W praktyce siatkę dyfrakcyjną otrzymuje się przez porysowanie płaskorównoległej płytki szklanej za pomocą diamentu szeregiem równoległych kresek. Nieprzezroczyste rysy odgrywają rolę zasłon, a przestrzenie między rysami to szczeliny. Jeśli na siatkę dyfrakcyjną prostopadle do jej powierzchni pada wiązka promieni równoległych to zgodnie z zasadą Huygensa, każda szczelina staje się źródłem kulistej fali ftórnej o tej samej częstości co fala pierwotna i wysyła promienie we wszystkich kierunkach, a więc nie tylko w kierunku promieni padających. Zjawisko to nazywa się dyfrakcją, czyli uginaniem prostoliniowego biegu promieni. Promienie ugięte mogą nakładać się czyli interferować ze sobą, gdyż są promieniami spójnymi, znaczy to że różnicy faz między nimi zależą tylko od różnicy dróg geometrycznych, nie zależą zaś od czasu. Biorąc pod uwagę wiązki promieni ugiętych zauważyć można, że w pewnych kierunkach promienie te będą się wzajemnie wzmacniały, w innych zaś wygaszały (częściowo lub zupełnie). Promienie ugięte będą się wzmacnić jeśli różnice dróg dwóch sąsiednich promieni będą równe całkowitej wielokrotności długości fali światła padającego. Warunek wzmocnienia promieni ugiętych ma postać: nl=dsina, gdzie d oznacza odległość między sąsiednimi szczelinami czyli tzw. stałą siatki dyfrakcyjnej, n jest to rząd widma (n = 1,2,3....).

2.Schemat uładu i przebieg ćwicenia

Celem ćwiczenia jest obliczenie d-szerokośći szczeliny. Aby to uczynić trzeba było obliczyć stałą siatki dyfrakcyjnej aby za jej pomocą obliczyć długość fali światła laserowego, która jest nam potrzebna do obliczenia szerokości szczeliny.

W pierwszej części ćwiczenia za pomocą spektrometru (ryc.1) znajdujemy kolejne kąty ugięcia. Umieszczamy siatkę dyfrakcyjną na stoliku spektrometru. Przez lunetę ustawioną na wprost kolimatora widzimy nieugięty obraz szczeliny. Patrząc w okular obracamy lunetę, aż ujrzymy w polu widzenia prążek pierwszego rzędu, Przy dalszym obrocie lunetki w tym samym kierunku można dojrzeć prążek drugiego i trzeciego rzędu. Obracając lunetkę w przeciwnym kierunku od położenia na wprost kolimatora ujrzymy także prążki I, II i III rzędu. Kierując krzyż lunetki tak aby zawsze pokrywał się z prążkiem notujemy kąty dla poszczególnych rzędów z lewej i z prawej strony od prążka zerowego.

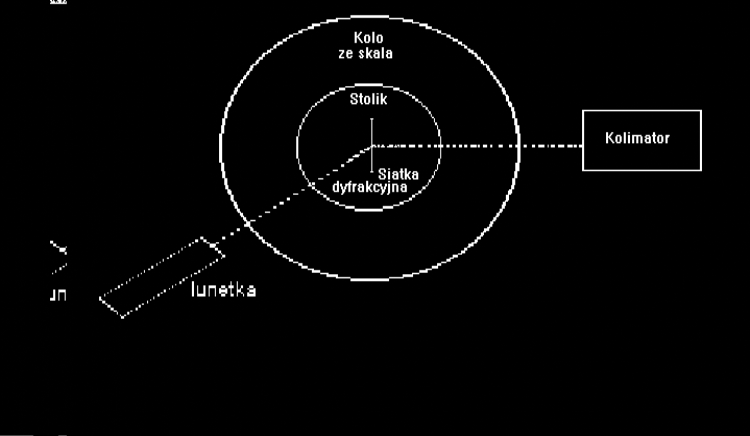
Rycina 1

W drugiej części ćwiczenia zmieżyliśmy za pomocą układu składającego się z lasera, siatki dyfrakcyjnej i ekranu (ryc.2) zależność odleglości prążków ugiętych po przepuszczeniu fali światła laserowego przez siatke dyfrakcyjną, od pozycji fali światła laserowego nieugiętego. Umieszczamy siatkę dyfrakcyją na stoliku prostopadle do kierunku padania światła i notujemy położenia kolejnych prążków dyfrakcyjnych dla trzech rzędów na lewo i prawo od prążka zerowego.

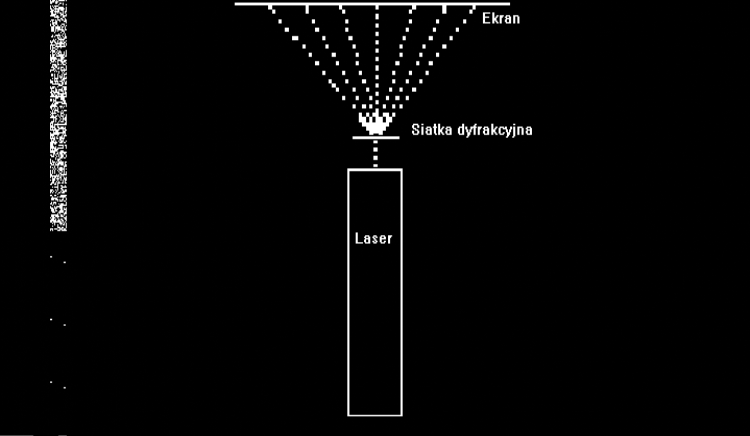
Rycina 2

Ostatnia część ćwiaczenia polegała na zbadaniu natężenia światla lasera przechodzącego przez szczelinę w zależności od polożenia.

3.Opis metody pomiarowej

W oparciu o powyższe (paragraf 1) rozważania możemy wyznaczyć stałą siatki dyfrakcyjnej posługując się laserem Helowo-Neonowym o znanej długości fali światła, siatką dyfrakcyjną i listwą pomiarową (ryc. 2) oraz spektrometrem (ryc.1)

Chcąc wyznaczyć stałą siatki dyfrakcyjnej musimy znać odpowiedający jej kąt ugięcia dający wzmocnienie fali świetlnej. W tym celu posługując się spektrometrem ustawiamy lunetke w pozycjach, w których następuje wzmocnienie fali światła sodowego przechodzącego przez siatkę dyfrakcyjną umieszczoną na stoliku spektrometru. Znając kąty ugięcia poszczególnych rzędów (n) możemy z warunku nl=dsinan obliczyć d czyli stałą siatki:
.

Chcąc obliczyć długość fali światła laserowego nie znając kątów ugięcia fali światła musimy analizując przebieg lini fali płaskiej (z założenia) światła po przejścu przez siatkę:
(1), gdzie l jest odległością siatki od ekranu, xn jest miejscem, w którym światło zostaje wzmocnione czyli zostaje spełnine równanie nl=dsinan (2). Podstawiając wzór (1) do wzoru (2) otrzymujemy równanie siatki dyfrakcyjnej:
. Z wzoru tego możemy już obliczyć długość fali światła:
.

Całe rozumowanie jest słuszne jedynie w przypadku, gdy płaszczyzna siatki jest równoległa do listwy pomiarowej, a wiązka światła prostopadła do płaszczyzny siatki.

Z równania siatki dyfrakcyjnej możemy obliczyć także szerokość szczeliny: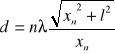
.

4. Obliczenia i rachunek błędów.

4.1. Stała siatki dyfrakcyjnej

Obliczamy kąt ugięcia
, gdzie an jest kątem ugięcia prążka n-tego rzędu, anl kątem prążka n-tego rzędu na lewo od prążka zerowego, anl kątem prążka n-tego rzędu na prawo od prążka zerowego.

Pomiary wykonano pięciokrotnie tak więc kąt, który będziemy brali po uwagę do dalszych obliczeń obliczamy ze wzoru na średnią arytmetyczną:
. Według powyższego wzoru wyliczono następujące wartości kąta ugięcia dla kolejnych prążków:

	Kąty ugięcia a []
Pomiar	1	2	3
1	6.35	13.50	20.35
2	6.35	13.30	20.00
3	6.20	13.20	20.15
4	6.50	13.20	20.35
5	6.35	13.00	20.20
śr.	6.35	13.20	20.21
max. Odchylenie	0.15	0.26	0.14

Pomiary dokonano z dokładnością do 1/3=0.(33)[]. Błąd ten jest większy od każdego z maksymalnych odchyleń od średnich dla kolejnych kątów, tak więc do obliczeń przyjęto błąd Da=1/3[]. Stałą siatki obserwowanego prążka wyznaczono z wzoru:
. Wstawiając dane otrzymano trzy stałe siatki. Błędy uzyskanych wartości l liczono z różniczki zupełnej: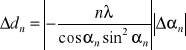
. Wstawiając za l średnią wartość długości fali żółtego dubletu sodu l=589.3 [nm], otrzymano trzy wartości d i Dd, z których obliczono średnią ważoną d i błąd błąd wyliczenia d: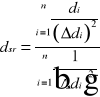
i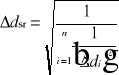

Wyniki jakie otrzymano to:

Obliczyć

n	1	2	3
d [nm]	5328	5146	5117
Dd [nm]	1615	769.4	526.1

Zatem ostatecznie: d= 5140±419.4 [nm].

4.2. Długość światła laserowego

Obiczamy długość światła laserowego ze wzoru: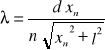
, gdzie
, d - warotść stałej siatki dyfrakcyjnej obliczonej w paragrafie 4.1. Błąd wyliczenia l obliczono metodą różniczki zupełnej:

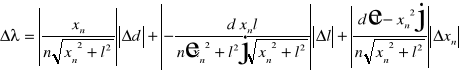
[m],

gdzie Dxn=0.08[m], Dl=0.005[m]. Następnie ze wzorów na średnią ważoną (paragraf 4.1), obliczono średnią długość światła laserowego. Uzyskano następujące wartości:

n	[m]	l[nm]	Dl[nm]
1	0.16150	648	72.6
2	0.33025	647	61.5
3	0.51550	644	57.3
śr.	---	646±36.3

Ostatecznie więc: l=646±36.3[nm].

4.3. Szerokość szczeliny

Obliczamy szerokość szczeliny ze wzoru: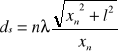
, gdzie l jest długością światła laserowego obliczona w paragrafie 4.2, xn to kolejne minima widma:

n	xlewe[cm]	xprawe[cm]	[cm]
1	3.583	20.541	4.042
2	6.333	17.708	6.792
3	9.125	14.833	9.792

Błąd wyliczenia d obliczono metodą różniczki zupełnej:

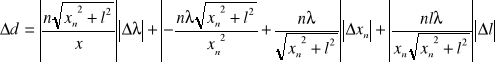
,gdzie Dl=0.005[m], Dl=0.3018[m], Dxn=0.08[m]. Następnie ze wzorów na średnią ważoną (paragraf 4.1) obliczono średnią szerokość szczeliny. Otrzymano nasępujące wyniki:

n	ds[nm]	Dds[nm]
1	14393	2835
2	144311	10966
3	145207	7673
śr.	14658±2833

Ostatecznie więc ds=14658±2833[nm].

5. Podsumowanie.

Szerokość szczeliny wyznaczono za pomocą lasera Helowo-Neonowewgo, którego długość fali wynosi:

l=646±36.3[nm],

oraz siatki dyfrakcyjnej, której stała wynosi:

d= 5140±419.4[nm],

Po podstawieniu do wzoru szerokość szczeliny wyniosła:

ds=14658±2833[nm].

Odchylenie wartości długości fali światła lasera liczona ze wzoru:
, gdzie lo=648[nm] wynosi d=0.31[%]. Odchylenie można więc uznać za małe, z czego można wnioskować że stała siatki dyfrakcyjnej jest również wyznaczona z dużą dokładnością. Dość dokładne wyznaczenie długości fali światła lasera i stałej siatki dyfrakcyjnej pozwala sądzić, że wyznaczenie szerokości

szczeliny jest obarczone nie dużym błędem.

---