SPRAWOZDANIE Z ĆWICZENIA NR 50

PIERWSZEJ PRACOWNI FIZYCZNEJ

OPRACOWAŁ : GONCERZ RAFAŁ

TEMAT : Wyznaczanie współczynnika samoindukcji i pojemności

przy pomocy obwodów prądu przemiennego

STRESZCZENIE

Dokument ten dotyczy sprawozdania z wykonania ćwiczenia nr 50 . Sprawozdanie to składa się z następujących części :

- wstępu teoretycznego

- wyników pomiarów

- opracowania wyników

- wniosków

- literatury

Dla wyrażniejszego zobrazowania wyników do sprawozdania dołączone zostały wykresy formatu A4.

I WSTĘP TEORETYCZNY

W obwodach prądu elektrycznego sinusoidalnie zmiennego , wraz z upływem czasu zmieniają się wartości napięcia i natężenia prądu zgodnie ze wzorami :

(1a)
(1b)

od wartości szczytowych dodatnich do wartości szczytowych ujemnych

gdzie :

Uo - wartości szczytowe napięcia

Io - wartości szczytowe natężenia prądu

- częstość kołowa zmian prądu

f - częstotliwość - częstość zmian prądu na sekundę

W obwodzie wyidealizowanym natężenie prądu It jest zgodne w fazie z napięciem Ut . Obwód rzeczywisty oprócz oporu omowego ( rezystancji ) stawia również opór samoindukcji (reaktancja indukcyjna ) oraz opór pojemnościowy ( reaktancja indukcyjna ) . Łączny opór obwodu prądu sinusoidalnie zmiennego ( zawada ) jest sumą geometryczną wymienionych już oporów .

(2) - zawada

(3) - reaktancja pojemnościowa

(4) - reaktancja indukcyjna

Ponieważ reaktancje indukcyjna i pojemnościowa są przeciwnie skierowane więc we wzorze na zawadę występuje kwadrat różnicy reaktancji (patrz rys.1)

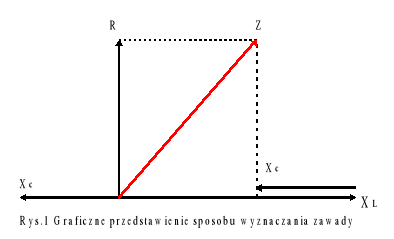
Gdy XL - XC =0 to mamy do czynienia z rezonansem w obwodzie prądu przemiennego . W przeciwnym wypadku mamy do czynienia z przesunięciem fazowym pomiędzy natężeniem prądu a napięciem . W zależności od tego czy większe jest XL czy XC , to albo natężenie prądu wyprzedza napięcie (XL >XC) lub napięcie wyprzedza natężenie prądu (XL <XC)

Przesunięcie fazowe oznaczamy . Wobec tego możemy zapisać wzór na zmianę prądu w czasie , podobnie jak i na zmianę napięcia :

(5)

Ze względu na swoją budowę , woltomierze i amperomierze nie wskazują wartości maksymalnych (szczytowych ) lecz skuteczne . Wobec powyższego aby poznać wartości szczytowe musimy pomnożyć wskazania mierników przez
.

II WYNIKI POMIARÓW

1. Wyznaczanie oporu omowego

cewka bez U [V] 0,050 0,060 0,075 0,100 0,125 0,150 0,200

rdzenia I [mA] 23 27 32 42 55 68 90

1

cewka z U [V] 0,050 0,100 0,150 0,200 0,250 0,300 0,400

dzeniem I [mA] 17 45 70 88 115 140 215

2. Wyznaczanie zawady

cewka bez U [V] 1 2 3 4 5 6 7

rdzenia I [A] 0,13 0,26 0,39 0,52 0,65 0,78 0,91

cewka z rdze- U [V] 3 4 5 6 7 8 9

niem otwartym I [A] 0,14 0,19 0,24 0,29 0,34 0,39 0,44

cewka z rdze- U [V] 3 4 5 6 7 8 9

niem zwartym I [A] 0,11 0,15 0,19 0,23 0,27 0,31 0,35

kondensator U [V] 5 6 7 8 9 10 11

I [A] 0,125 0,150 0,175 0,200 0,225 0,250 0,275

III OPRACOWANIE WYNIKÓW POMIARÓW

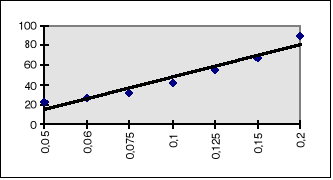
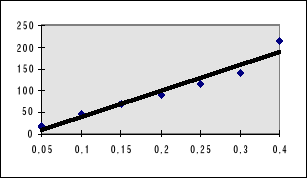
1. Wykreślam zależność I=f(U)

a ) dla cewki bez rdzenia - wykres nr 1

b ) dla cewki z rdzeniem - wykres nr 2

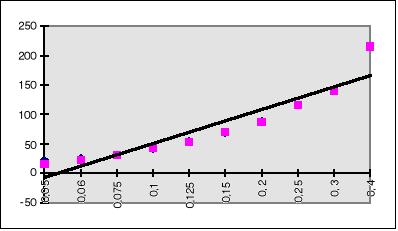
c ) zależność I = f(U) dla cewki z rdzeniem i bez rdzenia - wykres nr 2a - połączone wykresy numer 1 i 2

2. Wyznaczam współczynniki nachylenia wykresów metodą regresji liniowej , punkty przecięcia wykresu z osią OX oraz błędy wartości U. Korzystam ze wzorów :

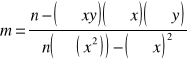
(6a)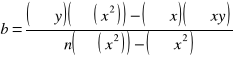
(6b)

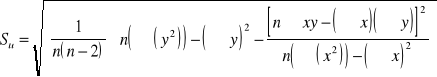
(6c)

a) dla wykresu nr 1

m =453,193 b = -1 SU = 1,441

b) dla wykresu nr 2

m =542,459 b = -13 SU = 8,377

3. Obliczam opór omowy w obwodzie prądu stałego korzystając ze wzoru :

(7)

Obliczam również błędy tych wartości korzystając ze wzoru na odchylenie standardowe:

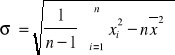
(8)

a ) dla cewki bez rdzenia R = 2,26

= 0,029

b ) dla cewki z rdzeniem R = 2,25

= 0,135

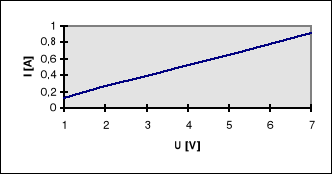
4.Wykreślam zależność Isk = f(Usk)

a) dla cewki bez rdzenia - wykres nr 3

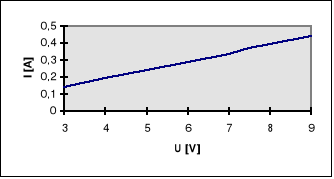
b) dla cewki z rdzeniem otwartym -wykres nr 4

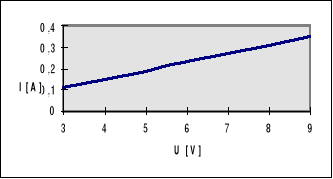
c) dla cewki z rdzeniem zwartym - wykres nr 5

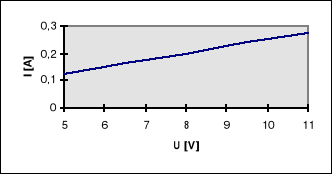
d) dla kondensatora - wykres nr 6

5. Wyznaczam nachylenie wykresów nr 3,4,5,6 metodą regresji liniowej , punkty przecięcia wykresu z osią OX oraz błędy wartości U - korzystam ze wzorów (6a,b,c)

a) dla cewki bez rdzenia - wykres nr 3

m= 7,692 b= 0 Su=0

b) dla cewki z rdzeniem otwartym -wykres nr 4

m=21,000 b=-0,01 SU=0

c) dla cewki z rdzeniem zwartym -wykres nr 5

m=26,000 b=-0,01 SU=0

d) dla kondensatora - wykres nr 6

m=40,000 b= 0 SU=0

6. Obliczam zawadę (w obwodzie prądu zmiennego) - korzystając ze wzoru :

(9)

a) dla cewki bez rdzenia Z= 7,692

b) dla cewki z rdzeniem otwartym Z=21,577

c) dla cewki z rdzeniem zwartym Z=26,255

d) dla kondensatora Z=40,000

7. W kolejności obliczam indukcyjności korzystając ze wzoru

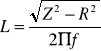
(10)

a) dla cewki bez rdzenia L= 23,40 mH

b) dla cewki z rdzeniem otwartym L=68,31 mH

c) dla cewki z rdzeniem zwartym L=83,27 mH

8. Następnie obliczam pojemność kondensatora - korzystam ze wzoru

(12)

Wyliczona wartość pojemności : C = 0,796 F

IV WNIOSKI

Różnice wartości w odczytanych wynikach prądów dla tych samych wartości napięcia przy obwodzie zasilanym prądem stałym (dla cewki bez rdzenia i dla cewki z rdzeniem ) wynikły z niestabilności blatu stołu na którym wykonywana była ta część ćwiczenia , oraz z powodu niedokładnego przylegania suwaka do zwojów opornicy suwakowej.Jak widać to na wykresie (2a) różnice te wcale nie są duże -w początkach wykresu różnią się bardziej - co widać po punktach przecięć z osią OX . Jak widać w następnym punkcie opracowania wyników , różnica oporów omowych mieści się w granicy sumy obu błędów .Z punktów 4-7 wynika , że po włożeniu rdzenia do środka uzwojenia cewki , zasilanej prądem przemiennym , wzrosły współczynniki nachylenia wykresów zależności I = f(U) , wzrosła indukcyjność cewki ( po włożeniu rdzenia zwartego zanotowałem większy wzrost indukcyjności - czego zresztą oczekiwałem), zmalało natężenie prądu płynącego przez cewkę przy jednoczesnym wzroście zawady.

V LITERATURA

1. T. Dryński - “ ĆWICZENIA LABOLATORYJNE Z FIZYKI ”

PWN Warszawa 1980 r.

“

2. A. Piekara - “ ELEKTRYCZNOŚĆ I MAGNETYZM

PWN Warszawa 1970 r.

“

3. E.M.. Purcell - “ ELEKTRYCZNOŚĆ I MAGNETYZM

PWN Warszawa 1974 r.

“

4. H. Szydłowski - “ PRACOWNIA FIZYCZNA

PWN Warszawa 1977 r.

---