Marcin Sroczyk
WPPT
Inżynieria Biomedyczna
Nr indeksu 93380
Pomiar wymuszonej aktywności optycznej
Ćwiczenie 89
Cel ćwiczenia: zapoznanie się ze zjawiskiem Faradaya, polegającym na indukowaniu polem magnetycznym dwójłomności kołowej w ośrodkach pierwotnie izotropowych, pomiar stałej Verdeta.
Wstęp teoretyczny
W 1845 r. Michael Faraday zaobserwował, że płaszczyzna polaryzacji światła, które przechodzi przez próbkę szkła typu flint, umieszczoną w polu magnetycznym, ulega skręceniu. Kąt skręcenia płaszczyzny polaryzacji jest proporcjonalny do indukcji magnetycznej B i do drogi światła w polu magnetycznym d :
= V B d
gdzie V - stała Verdeta.
Powyższy wzór jest słuszny w przypadku, gdy światło biegnie w kierunku równoległym do wektora indukcji B. Zjawisko skręcenia płaszczyzny polaryzacji w polu magnetycznym nazywamy zjawiskiem Faradaya albo sztuczną (wymuszoną) aktywnością optyczną. Zjawisko Faradaya występuje w ciałach stałych, cieczach i gazach. Zwykle wartość stałej Verdeta jest niewielka. Dużą wartość stałej V mają substancje o dużej dyspersji, np. niektóre gatunki szkieł i niektóre ciecze. Bardzo duże skręcenie płaszczyzny polaryzacji obserwuje się w cienkich warstwach metali ferromagnetycznych.
Różne substancje skręcają płaszczyznę polaryzacji w różnym kierunku. Substancjami prawoskrętnymi nazywamy te substancje, które skręcają płaszczyznę polaryzacji zgodnie z ruchem wskazówek zegara w stosunku do obserwatora, patrzącego wzdłuż wektora B w kierunku źródła światła. Natomiast substancje, które skręcają płaszczyznę polaryzacji w kierunku przeciwnym, nazywamy substancjami lewoskrętnymi. Gdy więc światło przechodzi przez ośrodek dwukrotnie, kąt skręcenia płaszczyzny polaryzacji podwaja się. Cecha ta odróżnia zjawisko Faradaya od naturalnej aktywności optycznej.
Zasada pomiaru.
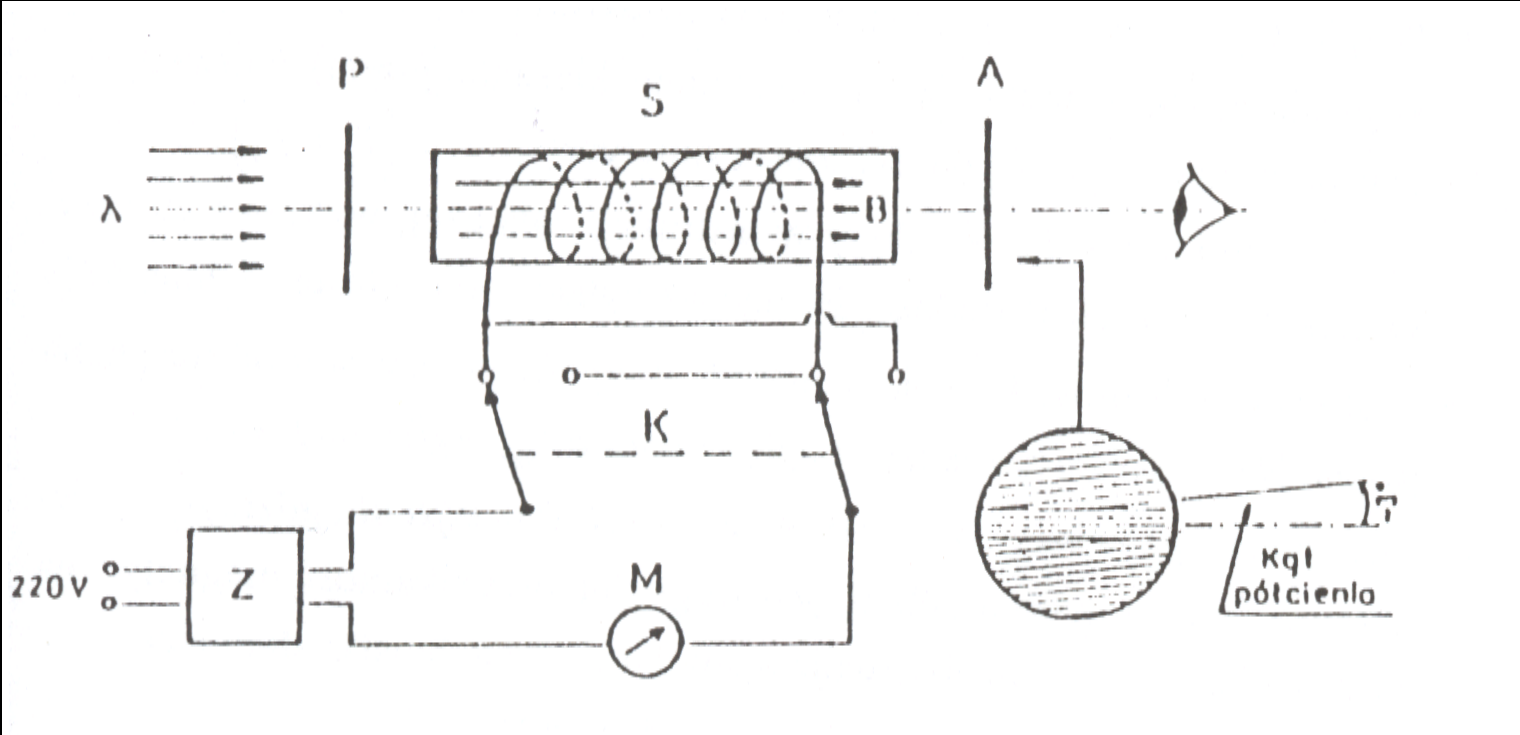
Do pomiaru zjawiska Faradaya stosuje się polaryskop, czyli urządzenie złożone z polaryzatora P i analizatora A. Między nimi mieści się solenoid z badanym obiektem. Analizator należy skrzyżować z polaryzatorem tak, aby uzyskać wygaszenie światła w polu widzenia. Analizator jest podzielony na trzy części. Kierunek przepuszczania części zewnętrznych tworzy z kierunkiem przepuszczania części środkowej tzw. kąt półcienia wynoszący około 3 stopni.
Układ do pomiaru wymuszonej aktywności optycznej: P - polaryzator, A - analizator, S - solenoid z prętem szkła w środku, λ - światło monochromatyczne, Z - zasilacz, K - przełącznik zmieniający kierunek przepływu prądu przez solenoid, M - miernik prądu
Tabele pomiarów i obliczenia
Parametry próbki SF3
Próbka |
|
SF - 3 |
Długość fali świetlnej |
|
589,3 nm |
|
Liczba zwojów |
n |
1230 |
|
Długość solenoidu |
l |
197 mm |
|
Długość próbki |
d |
160,00 mm |
Pomiar kąta przy wyłączonym prądzie płynącym przez solenoid.
Lp |
α [°] |
Δα [°] |
1 |
177,1 |
0,025 |
2 |
177 |
0,075 |
3 |
177,15 |
0,075 |
4 |
177,05 |
0,025 |
5 |
177,1 |
0,025 |
6 |
177 |
0,075 |
7 |
177,1 |
0,025 |
8 |
177,1 |
0,025 |
9 |
177,05 |
0,025 |
10 |
177,1 |
0,025 |
Średnia |
177,075 |
0,04 |
αn = 177,65 °
αn0śr = 177,075 °
Δα= (kl x z)/360° = 0,025°
Średnie odchylenie od wartości średniej Δαśr = 0,46 °
αn [° ] - w lewo |
αl = |α n - α0|[°] |
αn [° ] - w prawo |
αp = |α n - α 0|[°] |
I [A] |
||||||
1 |
2 |
3 |
śr |
|
1 |
2 |
3 |
Śr |
|
|
177,65 |
177,55 |
177,6 |
177,6 |
0,525 |
176,65 |
176,7 |
176,65 |
176,67 |
0,405 |
0,5 |
178,1 |
178,15 |
178,1 |
178,12 |
1,045 |
176,1 |
176,25 |
176,15 |
176,17 |
0,905 |
1,0 |
178,55 |
178,65 |
178,6 |
178,6 |
1,525 |
175,5 |
175,65 |
175,6 |
175,58 |
1,495 |
1,5 |
179,25 |
179,15 |
179,15 |
179,18 |
2,105 |
175,1 |
175,1 |
175,05 |
175,08 |
1,995 |
2,0 |
179,6 |
179,65 |
179,7 |
179,65 |
2,575 |
174,55 |
174,55 |
174,45 |
174,52 |
2,555 |
2,5 |
180,25 |
180,1 |
180 |
180,12 |
3,045 |
174,1 |
174,0 |
174,05 |
174,05 |
3,025 |
3,0 |
180,6 |
180,8 |
180,65 |
180,68 |
3,605 |
173,5 |
173,45 |
173,4 |
173,45 |
3,625 |
3,5 |
181,4 |
181,3 |
181,3 |
181,3 |
4,225 |
172,8 |
172,9 |
173 |
172,9 |
4,175 |
4,0 |
α = (αl + αp)/2
α [°] |
α [rad] |
I [A] |
0,465 |
0,008 |
0,5 |
0,975 |
0,017 |
1,0 |
1,510 |
0,026 |
1,5 |
2,050 |
0,036 |
2,0 |
2,565 |
0,045 |
2,5 |
3,035 |
0,053 |
3,0 |
3,615 |
0,063 |
3,5 |
4,200 |
0,073 |
4,0 |
Obliczając parametry prostej y=A+Bx metodą najmniejszych kwadratów otrzymujemy :
A = -0,00143 B = 0,01848
Indukcja magnetyczna w ośrodku
n = 998,985 zwojów / 0,160 m
μ0 = 4*π E-7 H/m
μ ≈ 1
I [A] |
B [T] |
0,5 |
627,68E-6 |
1,0 |
1255,36E-6 |
1,5 |
1883,04E-6 |
2,0 |
2510,72E-6 |
2,5 |
3138,40E-6 |
3,0 |
3766,08E-6 |
3,5 |
4393,76E-6 |
4,0 |
5021,45E-6 |
Stała Verdeta
d = 0,160 m.
I [A] |
α [rad] |
B [T] |
V [rad/T*m] |
0,5 |
0,008 |
627,68E-6 |
79,658 |
1,0 |
0,017 |
1255,36E-6 |
84,637 |
1,5 |
0,026 |
1883,04E-6 |
86,297 |
2,0 |
0,036 |
2510,72E-6 |
89,616 |
2,5 |
0,045 |
3138,40E-6 |
89,616 |
3,0 |
0,053 |
3766,08E-6 |
87,956 |
3,5 |
0,063 |
4393,76E-6 |
89,616 |
4,0 |
0,073 |
5021,45E-6 |
90,860 |
Vśr = 87,282 rad/T*m.
Wyznaczanie stosunku e/m elektronu.
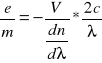
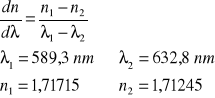
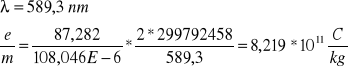
Spostrzeżenia i wnioski
W przypadku badanym w ćwiczeniu, światło padające na ośrodek aktywny jest spolaryzowane liniowo.
Można było zaobserwować skręcenie płaszczyzny polaryzacji pod wpływem pola magnetycznego wywołanego przepływem prądu.
Na podstawie pomiarów wyznaczono zależność kąta skręcenia płaszczyzny polaryzacji od prądu płynącego przez solenoid. Z zależności tej obliczono stałą Verdeta dla dwóch próbek szkła.
Wyznaczenie stałej Verdeta umożliwiło obliczenie stosunku ładunku do masy elektronu (e/m).
1
4