Sprawozdanie z ćwiczenia E-1.

Paweł Donarski	Zespół nr 17
Wydział Inż. Środowiska	Ocena z przygotowania:
Czwartek	Ocena ze sprawozdania:
Data :	Zaliczenie:
Prowadzący:	Podpis:

Temat: Badanie widma promieniowania termicznego na przykładzie żarówki z włóknem wolframowym.

Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z problemami związanymi z promieniowaniem termicznym, sprawdzenie słuszności prawa przesunięć Wiena oraz wyznaczenie rozkładów widmowych promieniowania włókna wolframowego żarówki dla kilku wybranych wartości temperatur.

Podstawy fizyczne.

Każde ciało w temperaturze powyżej zera bezwzględnego wysyła promieniowanie termiczne o widmie ciągłym. Promieniowanie to można obserwować w postaci widma, tak więc widmem nazywamy obraz zarejestrowanego promieniowania. Gdy temperatura nie przekracza 770K to widmo to składa się wyłącznie z promieniowania o długościach fal większych od zakresu widzialnego. Wraz ze wzrostem temperatury udział tego promieniowania wzrasta.

Modelem ciała emitującego promieniowanie termiczne jest ciało doskonale czarne.

Jest to ciało całkowicie pochłaniające energię padającą w całym zakresie widma. Zdolność absorbcyjna oraz emisyjna jest równa 1 z czego wynika, że ciało to emituje dokładnie tyle samo energii ile pochłania. Natomiast dla dowolnego ciała zdolność emisyjna wyraża się wzorem:

gdzie:

a - zdolność (liczba niemianowana wskazująca jaka część energii padającej jest absorbowana w jednostce czasu przez jednostkę powierzchni)

E - zdolność emisyjna ciała doskonale czarnego

Przekształcając powyższy wzór otrzymujemy prawo Kirchoffa:

Rozkład energetyczny promieniowania ciała doskonale czarnego znajdującego się w temperaturze T dany jest wzorem Plancka:

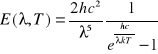
gdzie:

h - stała Plancka (6,62*
)

k - stała Boltzmana (
)

- długość fali

Zależność powyższa jest słuszna przy założeniu, że wypromieniowana energia jest w postaci kwantów.

Charakterystyczne dla rodziny krzywych opisanych wzorem Plancka jest istnienie maximów zdolności emisji, przy czym wraz ze wzrostem temperatury przesuwa się ono w kierunku fal krótkich. Okazuje się, że spełnione jest prawo:

gdzie:

- długość fali odpowiadająca maksimum zdolności emisji promieniowania ciała doskonale czarnego.

Powyższa zależność zwana jest prawem przesunięć Wiena.

Całkowita energia promieniowania wysyłana przez jednostkę powierzchni ciała doskonale czarnego w jednostce czasu wynosi:

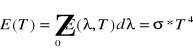
gdzie:

oznacz stałą Stefana-Boltzmanna

Opis ćwiczenia.

Do wyznaczenia rozkładu widmowego wykorzystany zostaje spektrometr Hilgera. Pozwala on na określenie długości fali padającego promieniowania. Do detekcji promieniowania użyty został fotorezystor, którego czułość zależy od długości fali padającej, a co za tym idzie należy wprowadzić stosowne poprawki. Temperatura włókna żarówki wyznaczona zostanie na podstawie pobieranej przez nią mocy. Pomiary długości fali zostały przeprowadzone dla trzech różnych temperatur w zakresie od 0,7 do 3
.

Opracowanie wyników.

Na podstawie zmierzonych wartości sporządziliśmy wykres zależności względnej zdolności emisyjnej od długości fali dla 3 różnych temperatur. Względna zdolność emisyjna wyraża się wzorem:

gdzie:

- wartość zdolności emisji znaleziona po uwzględnieniu poprawki na czułość rezystora:

s - czułość fotorezystora

- największa wartość

Z wykresu odczytaliśmy długość fali na która przypada maximum emisji.

Temperaturę włókna żarówki wyznaczyliśmy korzystając z zależności T(P), gdzie P=U*I.

Moc [W]	Temperatura [K]	[ ]
14.25 2 (14%)	1583 50	1.5 0.05
11.00 1.8 (16%)	1694 50	1.4 0.05
8.75 1.6 (18%)	1833 50	1.3 0.05

Sprawdzanie prawa przesunięć Wiena:

Temperatura [K]	[ ]	T*
1583 50	1.5 0.05	2375 154
1694 50	1.4 0.05	2372 155
1833 50	1.3 0.05	2383 157

Dyskusja błędów.

Przy szacowaniu błędów braliśmy pod uwagę tylko błędy systematyczne wynikające z niedokładności użytych przyrządów oraz błędy związane z odczytem z wykresów. Błędy liczyliśmy przy założeniach:

Błąd odczytu woltomierza:

0.325V (klasa=0.5 zakres=15V niedokładność odczytu=
0.25V)

Błąd odczytu amperomierza:

0.225A (klasa=0.5 zakres=5 niedokładność odczytu=
0.2A)

Błąd odczytu spektrometru:

=0.05

Błąd mocy wydzielanej na żarówce obliczyliśmy metodą pochodnej logarytmicznej:

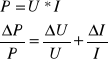
Błąd temperatury włókna żarówki odczytaliśmy z wykresu T(P), po uwzględnieniu błędu mocy.

Sprawdzając słuszność prawa przesunięć Wiena błąd iloczynu T*
oszacowaliśmy metodą różniczki zupełnej:

Wnioski.

W ćwiczeniu badaliśmy widmo promieniowania termicznego żarówki z włóknem wolframowym dla trzech różnych temperatur o zakresie fal od 0,7 do 3
(temperaturę otrzymaliśmy na podstawie wykresów T(P)). Pozwalało to na wyznaczenie długości fali, dla której zdolność emisyjna była największa. Otrzymane zależność zdolności emisyjnej od długości fal pokrywały się z wykresem teoretycznym za wyjątkiem skrajnych wartości długości fal. Przypuszczamy, że może to być spowodowane zbyt niską czułością fotorezystora na daną długość fali.

Otrzymane wyniki pozwalały na sprawdzenie prawa przesunięć Wiena. Obliczone iloczyny
były jednakowe (uwzględniając oszacowane poprzednio błędy), co potwierdza poprawność przeprowadzonych pomiarów i obliczeń.

Sprawozdanie z ćwiczenia E-1 strona 1

---