Kraków wrzesień 2002 r
Wartość nieregularnej wierzytelności kredytowej
Istota zagadnienia
Rozwój informatyki sprawił, że w procesach zarządzania stało się możliwe operowanie rachunkiem ekonomicznym daleko bardziej subtelnym i precyzyjnym niż było to wyobrażalne do niedawna. Precyzja rachunku ekonomicznego warunkuje precyzję i celność decyzji, czyli jakość i skuteczność zarządzania. Nic dziwnego, że coraz ostrzej rywalizujący konkurenci starają się z nowej szansy jak najskuteczniej korzystać. To wymaga zwiększonej ścisłości informacji oraz obiektywizacji metod obliczeniowych, co w szczególności dotyczy instytucji finansowych. Bankom staje się niezbędna znajomość realnej wartości ich aktywów, a przede wszystkim ich portfeli kredytowych. Jest bowiem oczywiste, że realna wartość portfeli kredytowych jest niższa od ich wartości nominalnej (rozumianej jako suma kapitału kredytu i spodziewanej wysokości uzyskanych w okresie kredytowania odsetek).
Żadna wierzytelność kredytowa nie charakteryzuje się prawdopodobieństwem spłaty równym jeden. Spłata jest tylko prawdopodobna; prawdopodobieństwo spłaty jest mniejsze od jedności. Zatem charakteryzująca dowolny kredyt wartość oczekiwana będąca iloczynem prawdopodobieństwa spłaty i kwoty należności jest w istocie niższa od wartości nominalnej. Tym bardziej realna wartość kredytów nieregularnych jest niższa od ich wartości nominalnej. Pomijanie obliczania realnej wartości tego rodzaju aktywów prowadzi do oczywistego rozmijania się z rzeczywistością. Przed bankami wyrasta więc zadanie znalezienia sposobów wyceny realnej wartości wierzytelności kredytowych, które żadną miarą nie powinny być kwalifikowane w bilansach banków na równi z pełnowartościowymi należnościami. Domagają się tego zresztą współczesne zasady rachunkowości.
Wierzytelności, w tym kredytowe, stały się specyficznym towarem. Handel nimi, co oczywiste, wymaga umiejętności wyceny ich wartości. Jeżeli przedmiotem transakcji są kredyty nieregularne, ich „cena” proponowana przez potencjalnego nabywcę będzie zazwyczaj wyraźnie niższa od wartości nominalnej. Dla sprzedającego powstaje problem: zaakceptować proponowaną stawkę czy zrezygnować z transakcji? Bankowy decydent powołany do rozstrzygania tego rodzaju dylematu, jest zawsze narażony na ryzyko zarzutu niegospodarności. Zatem chociażby dla własnego dobra powinien dysponować umiejętnością wyznaczania realnej wartości przedmiotu transakcji z punktu widzenia interesu swojej instytucji. Potrzebuje metody pozwalającej na racjonalne wyliczenie granicy „ceny”, poniżej której nie powinien akceptować propozycji.
W niniejszym opracowaniu prezentowana jest metoda temu celowi służąca. Jest to metoda określania takiego ułamka nominalnej wartości wierzytelności, poniżej której sprzedaż jest mniej korzystna niż przystąpienie do działań egzekucyjnych. Tak określony ułamek nominalnej wartości należności kredytowej może być uważany za obiektywną wartość nieregularnego kredytu z punktu widzenia interesu banku. Zrealizowanie transakcji przy „cenie” wyższej od tej granicy powinno być traktowane jako uzasadnione i racjonalne. Znajomość owej „minimalnej ceny” jest dla prowadzącego negocjacje w interesie banku istotną informacją.
Prezentowany tekst przedstawia podstawy teoretyczne proponowanej metody. Na tej podstawie została zrealizowana prosta wersja systemu obliczeniowego, który wykorzystano w praktycznej bankowej działalności.
Istota podejścia do określenia minimalnej ceny wierzytelności kredytowej
Określenie minimalnej ceny, poniżej której bank nie może zejść przy sprzedaży wierzytelności kredytowej, zostało oparte na założeniu, że finansowe skutki sprzedaży nie mogą być gorsze od finansowych skutków postępowania egzekucyjnego, z uwzględnieniem faktu, iż przepływy finansowe odsunięte w czasie od chwili bieżącej, względnie tracą na swej wartości zgodnie z zasadą relatywizmu wartości pieniądza w czasie. Skutki postępowania egzekucyjnego i skutki sprzedaży są zatem dyskontowane jako bilanse wartości bieżącej netto odpowiednio dla obydwu ścieżek działania, przy czym dla ścieżki sprzedaży bilans potraktowany zostaje parametrycznie jako funkcja ceny sprzedaży wierzytelności. Istota postępowania sprowadza się więc do określenia wartości bieżącej netto przyszłych strumieni finansowych związanych z postępowaniem egzekucyjnym (NPVw) oraz do wyznaczenia wartości bieżącej netto przyszłych strumieni finansowych związanych ze sprzedażą (NPVs) jako funkcji ceny sprzedaży wierzytelności i przyrównania ich do siebie, czyli
![]()
,
gdzie
cena sprzedaży wierzytelności.
Rozwiązanie powyższego równania określa taką cenę sprzedaży wierzytelności, która powoduje zrównanie wartości NPVs z wartością NPVw. Każda cena niższa od generuje wartość NPVs niższą od NPVw, co oznacza, że zrealizowanie na tych warunkach sprzedaży jest mniej korzystne od zrealizowania procedury egzekucyjnej. I to jest owa istotna dla strony sprzedającej wierzytelność informacja.
Metoda opiera się więc na prostej myśli przewodniej. Należy jednak jeszcze raz dobitnie podkreślić, iż wartość bieżąca netto NPVw wyrażająca spodziewany wynik finansowy wszczętych usiłowań egzekucyjnych to w danym przypadku nadzieja matematyczna, wyliczalna w przybliżeniu jako iloczyn prawdopodobieństwa sukcesu i kwoty będącej przedmiotem roszczenia. Zakłada się przy tym dla uproszczenia, że sukces oznacza uzyskanie pełnej kwoty roszczenia, a brak sukcesu pełną jej utratę. W ten sposób wartość oczekiwana rezultatu działań egzekucyjnych przybliża spodziewany realny wynik finansowy związany z realizacją windykacji.
Natomiast wejście banku na ścieżkę sprzedaży wierzytelności otwiera odmienną perspektywę przepływów strumieni finansowych. Przychód pojawia się tu w chwili bieżącej, a nie w mniej lub bardziej odległej przyszłości. Ujawnia się on w chwili bieżącej jako zdarzenie pewne. Stanowiącej ów przychód kwoty uzyskanej ze sprzedaży nie wystarczy jednak odnieść wprost do charakteryzującej skutek ekonomiczny przeprowadzenia procedury windykacji wartości bieżącej netto NPVw. Potrzebne jest uwzględnienie tej samej perspektywy czasowej, która jest określona dla ewentualnych działań egzekucyjnych. Chcąc więc wyliczyć wielkość wyniku finansowego sprzedaży, którą można by odnieść do rezultatu działań egzekucyjnych, trzeba przyjąć, iż środki finansowe uzyskane w rezultacie sprzedaży wierzytelności będą skierowane do obrotu bankowego (ze stopą zwrotu, którą osiąga bank w całym przekroju swojej działalności) na czas równy okresowi działań egzekucyjnych. Osiągany w ten sposób stopniowo dodatkowy dochód netto będzie powiększał kwotę osiągniętą w wyniku sprzedaży. Równocześnie jednak trzeba przyjąć, iż efekty tego obrotu będą odciążone normalnymi kosztami finansowymi. Oczywiście tu także musi być zastosowany mechanizm dyskontowania przyszłych strumieni finansowych na chwilę bieżącą, skąd właśnie wynika konieczność operowania wartością bieżącą netto NPVs.
Obliczenia i ich rezultaty będą istotnie się różnić w zależności od dwóch okoliczności
od tego czy bank w pełnym wymiarze swojej działalności osiąga zysk;
od tego czy działanie banku związane z konkretnym kredytem stającym się ewentualnie przedmiotem transakcji sprzedaży było poprawne, a więc czy ustanowiona w związku z nim rezerwa celowa może być zaliczona do kosztów uzyskania przychodów.
W związku z tym, w zaprezentowanym dalej mechanizmie obliczeniowym znajdują się dwa wskaźniki o charakterze incydentnym, a więc wskaźniki mogą przybierać wartość 0 lub wartość 1. Określanie minimalnej ceny sprzedaży wierzytelności kredytowej musi być poprzedzone zgodnym z rzeczywistością nadaniem wskaźnikom odpowiednich wartości liczbowych.
Pierwszy z nich będzie określał czy bank w momencie rozliczania rezultatów działań egzekucyjnych dotyczących danego kredytu osiąga w całej skali swojej działalności dodatni wynik finansowy, a więc czy jest płatnikiem podatku dochodowego. Zapiszemy więc
1 jeżeli bank, w całej skali prowadzonej działalności, osiąga dodatni wynik finansowy,
x =
0 w przeciwnym przypadku.
Rozróżnienie tego rodzaju alternatywy, rozstrzyga o tym czy obowiązek podatkowy banku ma charakter rzeczywisty czy tylko werbalny. Jeśli wynik finansowy banku jest ujemny, a więc bank nie płaci podatku dochodowego, podniesienie kosztu o utworzoną rezerwę celową czy też powiększenie dochodu banku (niewielkie przecież w ogólnej skali obrotów bankowych) o finansowy efekt sprzedaży wierzytelności nie powoduje zwiększonego obciążenia podatkowego. Jeśli zaś ogólny wynik banku jest dodatni, wówczas zwiększenie o rezerwę celową kosztów banku obniży podstawę opodatkowania podatkiem dochodowym i spowoduje odprowadzenie odpowiednio niższej kwoty podatku. Natomiast w następstwie dokonanej sprzedaży bank zapłaci podatek dochodowy od dochodu osiągniętego ze sprzedaży. Jeśli bank osiąga stratę w swojej działalności, dochód będący konsekwencją sprzedaży wierzytelności nie pociągnie za sobą obowiązku podatku dochodowego (poza szczególnym przypadkiem gdy przychód ze sprzedaży pokryje akurat stratę banku i spowoduje dodatnie saldo wyniku finansowego; taka sytuacja jest jednak tak mało prawdopodobna, że można nie brać jej pod uwagę). W celu uwzględnienia tego rozróżnienia prowadzący obliczenia winien przyjąć x=1, gdy bank w całej skali prowadzonej działalności osiąga zysk i w konsekwencji jest obciążony podatkiem dochodowym, albo liczbę x=0, gdy bank nie osiąga zysku.
Druga istotna dla prowadzonych obliczeń alternatywa sprowadza się do kwestii, czy bank ma czy też nie ma swego udziału w przyczynach tego, że dany kredyt stał się kredytem nieregularnym. Bank może zaliczyć utworzoną rezerwę celową do kosztów uzyskania przychodów tylko wtedy, gdy jego działanie na etapie udzielania kredytu i dalej - w trakcie prowadzenia kredytu - było właściwe, a znalezienie się kredytu w kategorii kredytów nieregularnych nie zostało przez bank zawinione. Zatem jeśli bank ponosi część winy za kłopoty związane z danym kredytem, będzie ukarany opodatkowaniem w całości dochodów osiągniętych w rezultacie windykacji czy sprzedaży wierzytelności, gdy w przypadku przeciwnym zapłaci podatek od kwoty odpowiednio niższej, gdyż pomniejszonej o koszty uzyskania przychodu. Tę okoliczność wyrazi następny incydentny wskaźnik
1 jeżeli brak obsługi kredytu nie został spowodowany wadliwym działaniem banku,
y =
0 w przeciwnym przypadku.
Prowadzący obliczenia winien nadać współczynnikowi liczbową wartość y=1, gdy historia kredytu wskazuje, że bank jest bez winy, a więc może zaliczyć utworzoną rezerwę celową do kosztów uzyskania przychodu. Natomiast gdy z analizy dokumentacji kredytowej będzie wynikać, iż w związku z określonymi popełnionymi nieprawidłowościami nie jest możliwe potraktowanie poniesionych przez bank wydatków jako kosztu uzyskania przychodów, współczynnik musi być określony jako liczba y=0. W zależności od zapisanej liczby, rezerwa celowa utworzona w związku z danym kredytem będzie lub nie będzie zaliczona do kosztów uzyskania przychodów, co - rzecz jasna - będzie mieć wpływ na poziom salda wyniku finansowego, a także na wartość minimalnej ceny wierzytelności.
Wielkości charakteryzujące sytuację kredytu w chwili bieżącej
Kredyt nieregularny ma swoją przeszłość. W momencie, w którym ma zapaść decyzja co do dalszych jego losów, znane są charakteryzujące go podstawowe wielkości: kwota należnego bankowi kapitału kredytowego i niezapłaconych odsetek, wysokość utworzonej rezerwy celowej. Wielkości te muszą odpowiednio uczestniczyć w procesie obliczeniowym, który będzie ukazywany w logicznym porządku, wyznaczanym odpowiednimi formułami matematycznymi. W pierwszej kolejności scharakteryzowane zostaną podstawowe wyliczenia dotyczące niejako przeszłości, czyli charakteryzujące sytuację kredytu w chwili bieżącej.
Należny kapitał kredytowy: K
Kapitał pozyskany w celu udzielenia kredytu
![]()
,
gdzie
r - stopa rezerwy obowiązkowej.
Konieczność odprowadzenia rezerwy obowiązkowej sprawia, iż bank musi pozyskać kwotę KP kapitału odpowiednio większą od kwoty kredytu K.
Odprowadzona rezerwa obowiązkowa
![]()
Należne, nie wpłacone do banku odsetki kredytowe: KO
Utworzona rezerwa celowa
![]()
,
gdzie
c - współczynnik określający jaka część niespłaconego kapitału kredytowego została pokryta rezerwą celową.
Efekt podatkowy
![]()
,
gdzie
d - stopa podatku dochodowego
x - wskaźnik incydentny
W rezultacie utworzenia rezerwy celowej w kwocie C1 bank zapłacił w przeszłości podatek dochodowy niższy o kwotę D1.
Wartość bieżąca netto NPVw charakteryzująca wynik postępowania egzekucyjnego
Dokonamy teraz prezentacji rozumowania umożliwiającego symulację finansowych skutków postępowania egzekucyjnego. Wprowadzone i omówione w naturalnym ciągu logicznym zostaną kolejne wielkości i formuły, z których zbudowane zostanie ostatecznie równanie NPVw.
Koszty egzekucyjne
![]()
,
gdzie
a - współczynnik wyrażający wielkość kosztów egzekucyjnych w stosunku do kwoty należności.
Kapitał pozyskany w celu pokrycia kosztów egzekucyjnych,
![]()
Bank bowiem, który musi pokryć koszty egzekucyjne (zazwyczaj z góry), nie ma innej możliwości jak pozyskać potrzebną kwotę na zwykłych zasadach z zewnątrz.
Odprowadzona rezerwa obowiązkowa od tego kapitału
![]()
Należne odsetki ustawowe za czas prowadzonych działań egzekucyjnych
![]()
,
gdzie
u - stopa odsetek ustawowych,
N - okres prowadzenia działań egzekucyjnych (w latach)
Suma należności podlegających egzekwowaniu
![]()
Wartość oczekiwana kwoty uzyskanej z windykacji
![]()
,
gdzie
p - prawdopodobieństwo, że statystyczna jednostka wartości (np. 1 zł) z kwoty należnej bankowi zostanie uzyskana na drodze prowadzonych działań egzekucyjnych.
Pokrycie należności z tytułu zwrotu kosztów egzekucyjnych
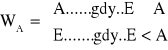
Współczynnik pokrycia:
![]()
Pokrycie należności z tytułu odsetek ustawowych
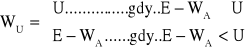
Współczynnik pokrycia:
![]()
Pokrycie należności z tytułu odsetek kredytowych
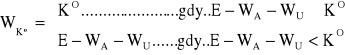
Współczynnik pokrycia:
![]()
Pokrycie należności z tytułu zwrotu podstawowego kapitału kredytowego
![]()
Współczynnik pokrycia:
![]()
Koszty uzyskania przychodu
![]()
Koszty uzyskania przychodu zerują się gdy wartość wskaźnika y jest równa zero.
Wynik finansowy
![]()
Efekt podatkowy związany z efektem działań winydykacyjnych
![]()
Obciążenie banku podatkiem dochodowym zaistnieje tylko w przypadku, gdy osiąga on w całej skali prowadzonej działalności dodatnie saldo wyniku finansowego (x=1). Należy zarazem zauważyć, iż w razie gdy efekt podatkowy D2 okaże się liczbą ujemną, wielkość tego efektu pomniejszy odpowiednio płaconą przez bank kwotę podatku dochodowego w momencie finalnych rozliczeń dotyczących danego kredytu.
Kapitał zwrócony depozytariuszom: KP
Odzysk kwot rezerw obowiązkowych
![]()
Jest istotne, że przepływy finansowe związane z wyżej scharakteryzowanymi wielkościami następują w różnym czasie. Jedne miały miejsce w przeszłości w stosunku do momentu rozważania ewentualności wszczęcia działań egzekucyjnych, inne związane są niejako z owym momentem, a jeszcze inne dopiero nastąpią w przyszłości. Konieczne jest zdyskontowanie przyszłych (w stosunku do chwili bieżącej) przepływów finansowych właśnie na chwilę bieżącą. Dotyczy to w szczególności kosztów obsługi kapitału pozyskanego w celu udzielenia kredytu oraz na pokrycie kosztów egzekucyjnych oraz przepływów finansowych związanych z rozliczeniami końcowymi.
W związku z naturalnym faktem, iż koszty związane z dysponowaniem przez bank cudzym kapitałem powstają w ustalonym rytmie czasowym, zachodzi potrzeba dyskontowania przyszłych strumieni finansowych na chwilę obecną, stosownie do właściwej stopy dyskontowej oraz odległości w czasie momentów zaistnienia tych przepływów finansowych w stosunku do chwili bieżącej. Zabieg dyskontowania ponoszonych przez bank kosztów kapitałowych wyraża równanie
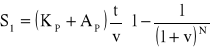
,
gdzie
t - wypadkowa stopa procentowa, po której bank pozyskuje kapitał („koszt pieniądza”) ,
v - wypadkowa stopa zwrotu osiągana przez bank w prowadzonym obrocie kapitałowym (tutaj - stopa dyskontowa).
Aktualną wartość strumieni przepływów finansowych wynikających z końcowych rozliczeń obliczymy natomiast w oparciu o równanie
![]()
.
To pozwala ostatecznie określić wartość bieżącą netto NPVw charakteryzującą spodziewany rezultat finansowy sprawy kredytowej zakończonej postępowaniem egzekucyjnym, mianowicie
![]()
.
Taką wartość przedstawia dla banku w chwili bieżącej perspektywa zrealizowania ścieżki postępowania egzekucyjnego.
Wartość bieżąca netto NPVs jako funkcja ceny wierzytelności
Alternatywą postępowania egzekucyjnego jest sprzedaż wierzytelności, jeśli tylko otwiera się taka możliwość. Atrakcyjność tej perspektywy zależy od osiągniętej ceny sprzedaży. Końcowy rezultat zrealizowania tej ewentualności powinien być nie gorszy od rezultatu działań egzekucyjnych, gdyż w przeciwnym przypadku nie powinno dojść do sprzedaży. Istota poszukiwań sprowadza się do znalezienia takiej granicznej ceny sprzedaży wierzytelności, która zapewni wartość NPVs równą NPVw. Każda cena wyższa od owej ceny granicznej przesądza o wyższej ekonomicznej efektywności decyzji sprzedaży wierzytelności nad decyzją jej windykowania.
Podstawą prawidłowości obliczeń zmierzających do wyznaczenia granicznej ceny wierzytelności jest porównywalność obydwu wartości bieżących netto, czyli NPVw i NPVs. Ten warunek będzie spełniony, jeśli - co już podkreślaliśmy - następstwa sprzedaży wierzytelności zostaną skwantyfikowane odpowiednio dla okresu czasu równego okresowi, w jakim prowadzone byłyby działania egzekucyjne. Oznacza to w szczególności konieczność założenia, iż środki finansowe uzyskane w następstwie aktu sprzedaży będą skierowane do zwykłego obrotu bankowego dostarczając odpowiednio dodatkowych przychodów, a bank zarazem będzie ponosił koszty z tym związane. A oto sekwencja formuł definiujących wielkości, które będą musiały wystąpić w tym rachunku, począwszy od momentu pojawienia się w banku kwoty uzyskanej ze sprzedaży (wielkości charakteryzujące przeszłość są identyczne jak poprzednio).
Przychód ze sprzedaży wierzytelności
![]()
,
gdzie
α - graniczna cena wierzytelności
Koszt uzyskania przychodu
![]()
Wynik finansowy
![]()
Efekt podatkowy
![]()
Uwolniona kwota kapitału
![]()
Zwrot kapitału kredytowego: KP
Odzysk rezerwy obowiązkowej: R1
Należy przyjąć, iż także w tym przypadku bank będzie ponosił normalne finansowe obciążenia wynikające z czasowego dysponowania cudzym kapitałem, a więc będzie powadził finansową obsługę kapitału kredytowego w czasie równym okresowi trwania postępowania egzekucyjnego, a także podda obrotowi bankowemu kwotę uwolnioną w wyniku dokonanej sprzedaży wierzytelności. Te strumienie finansowe, jak również strumienie rozliczeń końcowych trzeba zdyskontować.
Bank w efekcie prowadzonego obrotu finansowego kwotą Kw powiększy ją do kwoty, której bieżąca wartość netto będzie wynosić
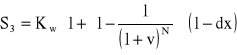
.
Założono przy tym, iż bank w obrocie finansowym prowadzonym kwotą Kw będzie osiągał typową dla swojej sytuacji w danym czasie stopę zwrotu równą v; tę samą, która jest tu zarazem traktowana jako stopa dyskontowa. Uwzględniono przy tym fakt, iż także od tak osiągniętego dochodu bank będzie obciążony podatkiem dochodowym.
Bank równocześnie ponosi koszty finansowe (koszt pieniądza) w wysokości
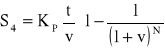
.
Na końcu okresu obliczeniowego bank dokona finalnych rozliczeń, których wartość bieżąca netto będzie wynosić
![]()
.
Ostatecznie można zapisać, iż bank w następstwie sprzedaży wierzytelności kredytowej po „cenie” osiągnie wynik finansowy, którego wartość bieżąca netto wyniesie
![]()
.
Minimalna cena tej wierzytelności, to taka cena, dla której obydwie wartości NPV są równe. Gdyby bank sprzedał wierzytelność taniej, mógłby powstać zasadny zarzut, iż postąpił nieracjonalnie czy wręcz niegospodarnie.
Minimalna cena sprzedaży wierzytelności kredytowej
Wielkość NPVs() jest funkcją minimalnej ceny wierzytelności. Mimo dość złożonej postaci tej funkcji ma ona charakter liniowy. Zatem, przyrównanie NPVs() do NPVw tworzy równie liniowe. Rozwiązanie go ze względu na zmienną wskazuje dla jakiej wartości ceny sprzedaży efekt sprzedaży wierzytelności jest identyczny z efektem windykacji.
Ów proces obliczeniowy, acz prosty w swojej istocie, jest algebraicznie dość skomplikowany. Nie jest to istotne w sytuacji, gdy obliczenia są prowadzone numerycznie. Świetnym informatycznym narzędziem dla tego rodzaju obliczeń jest arkusz kalkulacyjny EXCEL. Instrument ten jest całkowicie wystarczający dla profesjonalnego wyznaczania minimalnej ceny sprzedaży wierzytelności kredytowej.
Interesująca może być charakterystyka podstawowych zależności minimalnej ceny od liczbowych wartości warunkujących ją niektórych parametrów. Podstawową jest zależność minimalnej ceny od prawdopodobieństwa sukcesu działań egzekucyjnych. Im prawdopodobieństwo sukcesu większe, tym wyższą staje się minimalna cena, co ilustruje wykres (rys. 1).
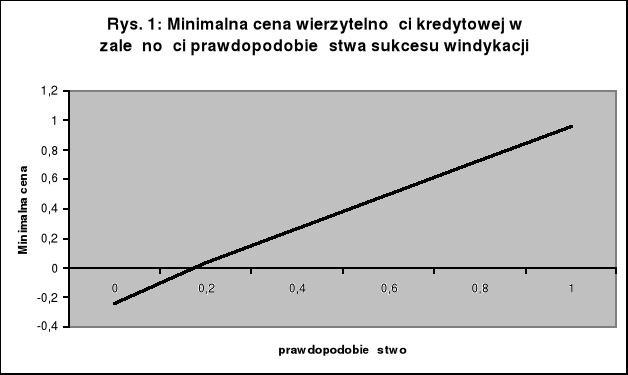
Warto zwrócić uwagę na fakt, że gdy prawdopodobieństwo sukcesu jest bliskie jedności, minimalna cena sprzedaży kredytu zbliża się do jedności, czyli do nominalnej wartości wierzytelności. Natomiast gdy prawdopodobieństwo sukcesu jest znikome, dla banku jest opłacalne podyktowanie nawet ujemnej ceny, czyli dopłacenie do wierzytelności, która z punktu widzenia jego interesu jest niemal bezwartościowym balastem. Mniejszym złem staje się dla banku oddanie takiej wierzytelności za niewielką dopłatą niż prowadzenie beznadziejnych działań windykacyjnych wiążących się z relatywnie niemałymi kosztami. Ujemna cena wyzbycia się straconej wierzytelności kredytowej może być w takiej sytuacji rozwiązaniem racjonalnym. Prawdopodobieństwo sukcesu windykacji jest czynnikiem określającym poziom minimalnej ceny sprzedaży nieregularnego kredytu o najsilniejszym oddziaływaniu. Można też powiedzieć, iż wrażliwość minimalnej ceny na prawdopodobieństwo sukcesu postępowania egzekucyjnego jest najwyższa.
Minimalna cena wierzytelności kredytowej jest wielkością zależną bezpośrednio od sytuacji ekonomicznej banku. Jeśli bank znajduje się w dobrej kondycji, osiąga w ogólnej skali swojej działalności przyzwoitą stopę zwrotu. W takiej sytuacji wymagania dotyczące efektywności ewentualnej transakcji dotyczącej nieregularnego kredytu będą odpowiednio wysokie, czego konsekwencją będzie relatywnie wysoka wartość zastosowanej w obliczeniach stopy dyskontowej. Spadek osiąganej generalnie przez bank stopy zwrotu będzie sprawiał, iż będzie on się zadowalał zarazem relatywnie niższą stopą dyskontową zastosowaną w obliczeniach prowadzących do znalezienia minimalnej ceny sprzedaży. Nie będzie to bez wpływu na wartość minimalnej ceny wierzytelności, o czym przekonuje przedstawiona na wykresie (rys. 2) przykładowa krzywa wyrażająca minimalną cenę wierzytelności w zależności od stopy dyskontowej.
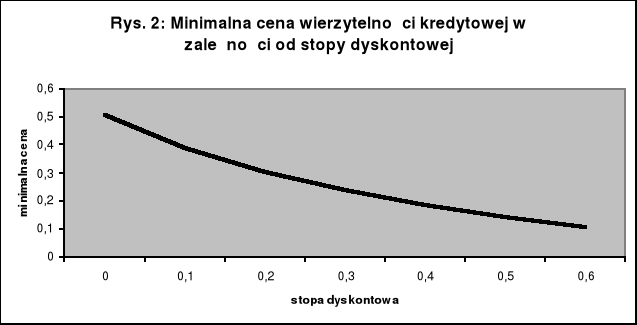
Jak widać, podwyższanie wartości stopy dyskontowej prowadzi do obniżania się minimalnej ceny sprzedaży wierzytelności. Wartość minimalnej ceny maleje asymptotycznie do zera, gdy wartość stopy dyskontowej zmierza do nieskończoności. Jest to konsekwencja zmierzania do zera wartości NPVw w następstwie zmierzania do nieskończoności stopy dyskontowej. Wypływa stąd wniosek, iż dany kredyt przedstawia dla banku względnie tym mniejszą wartość, im lepszą jest jego sytuacja ekonomiczna wyrażająca się odpowiednio wysoką wartością stopy dyskontowej.
Skoro stopa rezerwy obowiązkowej jest parametrem w obliczeniach, można zadać pytanie o wrażliwość minimalnej ceny wierzytelności na jej zmiany. Odpowiada na nie obrazowo kolejny wykres (Rys. 3).
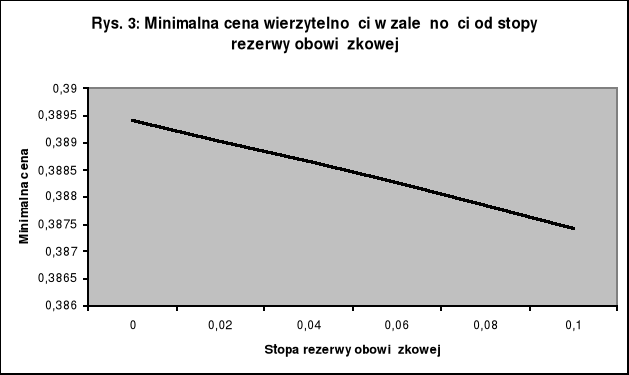
Wykres ujawnia, iż zależność ta istnieje, jest jednak znikoma w przedziale wartości realnie wyobrażalnych w normalnych warunkach gospodarczych. Krzywa w tym wąskim przedziale wartości stopy rezerwy obowiązkowej jest bardzo zbliżona do prostej. Jeżeli jednak rozważyć teoretycznie przedział wartości tej stopy z pogranicza liczby 1, ujawnia się szczególna nieliniowość krzywej. Właściwość ta wynika z istoty rezerwy obowiązkowej, a konkretnie z mechanizmu jej powstawania. Bank chcąc pozyskać kapitał, którym mógłby realnie dysponować, w kwocie K, musi dodatkowo pozyskać kapitał w kwocie R, która będzie odprowadzona jako rezerwa obowiązkowa
![]()
,
gdzie
r - stopa rezerwy obowiązkowej.
Bank w celu uruchomienia kredytu w kwocie K musi pozyskać na rynku finansowym kapitał w kwocie K+R. Jeśli stopa r zbliża się do jedności, mianownik ukazanej wyżej ułamkowej formuły zbliża się do zera, a zatem kwota rezerwy R zmierza do nieskończoności. Przy stopie rezerwy obowiązkowej r bliskiej zera bank musi zamrażać w postaci rezerwy niemal cały pozyskany kapitał. Zdyskontowany wynik finansowy banku w takiej sytuacji musi zmierzać do minus nieskończoności, a w konsekwencji i minimalna cena sprzedaży musi zmierzać do minus nieskończoności. Pokazuje ten fakt następny wykres (rys. 3') będący wariantem poprzedniego, różniącym się jedynie użytym w tym przypadku innym przedziałem wartości zmiennej niezależnej; tu pokazano przebieg krzywej wartości minimalnej ceny wierzytelności dla przedziału wartości rezerwy obowiązkowej [0,7 - 0,99].
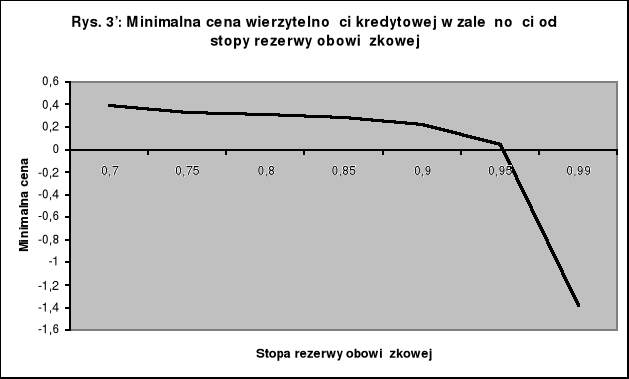
Kształt krzywej, w szczególności ostrość regresu minimalnej ceny w miarę wzrostu stopy rezerwy obowiązkowej zależy od sytuacji banku, którą tu wyraża ogół wyżej sygnalizowanych parametrów obliczeniowych określających wartość NPVw i NPVs. Oczywiście użyty tu przedział wartości rezerwy obowiązkowej, to tylko abstrakcja. Przywołujemy ją wyłącznie w celu pełniejszego ukazania natury zależności minimalnej ceny wierzytelności od wartości stopy rezerwy obowiązkowej. Jak widać, wbrew pierwszemu wrażeniu, nie jest to zależność liniowa.
Zgoła inaczej wpływa na minimalną cenę wierzytelności kredytowej stopa rezerwy celowej, czyli po prostu ułamek nominalnej wartości kapitału kredytowego. Jak łatwo się domyślić, wartość wierzytelności wyrażająca się jej minimalną ceną jest tym niższa, im wyższą rezerwę celową dla niej utworzono. Przekonuje o tym wykres (rys. 4). Odpowiada on przykładowo na pytanie, jaką powinna być minimalna cena wierzytelności kredytowej przy stopie rezerwy celowej przebiegającej cały przedział [0,1], a więc gdy utworzona rezerwa celowa przyjmuje wartości od zera do pełnej kwoty kapitału kredytowego. Ta zależność ma liniowy charakter.
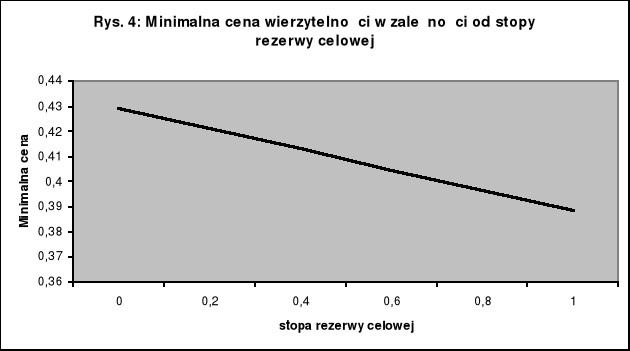
Jak widać, minimalna cena sprzedaży kredytu maleje wraz ze wzrostem utworzonej dla niego rezerwy celowej. Zależność ta nie jest tu silna. Gdyby jednak przyjąć, że bank nie może wliczyć rezerwy celowej do kosztu uzyskania przychodu, regres minimalnej ceny w miarę wzrostu stopy rezerwy celowej byłby intensywniejszy.
Minimalna cena wierzytelności kredytowej może być traktowana jako obiektywna miara wartości kredytu pozostającego w sytuacji nieregularnej. Wydaje się istotne, by zobiektywizowane wartości nieregularnych wierzytelności stawały się podstawowym elementem baz danych charakteryzujących portfele kredytowe banków. Nasuwa się równocześnie myśl, iż podobnie (choć nie identycznie) można urealniać wartość każdego kredytu pozostającego w sytuacji normalnej. Każdy statystyczny kredyt cechuje się bowiem prawdopodobieństwem spłaty mniejszym od zera. Ponadto związane z nim przepływy finansowe są odpowiednio odsunięte w czasie, co niejako obniża ich realną wartość. O wartości kredytu winien więc przesądzać rachunek wartości bieżącej netto potraktowany jako nadzieja matematyczna uwarunkowana prawdopodobieństwem prawidłowej spłaty kapitału i odsetek w wyznaczonych terminach. Ważnym będzie również zweryfikowanie przydatności przedstawionej metody do wyceny instrumentów pochodnych, kredytu kupieckiego i innych aktywów finansowych.
Wystarczy przeanalizować zapisy obowiązującej w Polsce nowej „Ustawy o rachunkowości” z 2001 roku oraz niektórych aktów wykonawczych jak „Rozporządzenie Ministra Finansów z 10 grudnia 2001 r. w sprawie zasad tworzenia rezerw na ryzyko związane z działalnością banków” (wcześniej - z odnośnych aktów prawnych Prezesa NBP i Przewodniczącego Komisji Nadzoru Bankowego).
czyli pewien ułamek nominalnej wartości wierzytelności; ułamek ten w dalszym ciągu będzie konsekwentnie nazywany ceną sprzedaży
w rozumieniu postępowania windykacyjnego obejmującego całokształt działań, których elementem jest procedura egzekucyjna (komornicza).
W danym równaniu, a także w następnych, występuje czynnik stanowiący sumę wyrazów ciągu geometrycznego o postaci:![]()
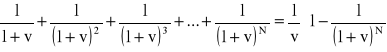
to i następne zdania w tym akapicie, są co oczywiste jedynie teoretyczną prawidłowością. W realnym wymiarze wierzyciel nie oddaje swoje należności za dopłatą lecz podejmuje decyzję o odpisaniu jej w straty z umorzeniem (jeżeli jest bardziej ostrożny to bez umorzenia mając na względzie perspektywę powrotu do oceny sytuacji w przyszłości), bez wszczynania kosztownych procedur egzekucyjnych, opierając się na normie ustawy o podatku dochodowym od osób prawnych uprawniającej do takiego zachowania w sytuacji kiedy koszty egzekucji będą wyższe od spodziewanych do uzyskania w jej toku kwot.
Jest to w pełni zrozumiałe, zważywszy że prezentowana idea opiera się na zainwestowaniu przez Bank w swoje produkty kredytowe środków finansowych uzyskanych przez sprzedaż wierzytelności. Jeżeli rentowność aktywów jest wysoka, kredyt nieregularny można sprzedać za niższą cenę niż gdy ta rentowność jest niższa, bowiem w przewidywanym okresie windykacji uzyska się identyczny wynik finansowy z wykonanego obrotu
oczywiście w sytuacji kiedy prawdopodobieństwo sukcesu windykacyjnego jest stałe
8
Wyszukiwarka
Podobne podstrony:
Ustawa z dnia 29 pazdziernika 2001 r, smieszne teksty
Wzory druków i umów, Zwrot akt po przedł. doch., Dnia października 2001 r
Kredyt konsumencki Dz U 2001 1
Mkroekonomia T Zalega, E Krakowska W wa 2001 2002(1)
pazdziernik 2001
pazdziernik 2001
Miesiecznik Krakow Pazdziernik 2015 s 2y02
D19220799 Ustawa z dnia 19 września 1922 r zezwalająca reprezentacji powiatowej w Chrzanowie na zac
D19200410 Obwieszczenie Ministra Skarbu w przedmiocie wydawania przez Miejski Zakład Kredytowy w Kr
BEZROBOCIE W POLSCE W PAŹDZIERNIKU 2001 ROKU
2001 październik Cztery pory roku kryteria
1 12, Kraków, 22 października 1999
3 9, Kraków, 01 października 1997
AKADEMIA EKONOMICZNA W KRAKOWIE o konflikcie wartości
STUDIUM dla kredytu od 1500 tys, PKO Bank Polski SA, Oddział 12 w Krakowie,
Utrata wartości kredytu
4 6, Kraków, 01 października 1997
Wycena papierów wartościowych, Kredyty
Zabezpieczenia prawne kredytów – zabezpieczenia osobiste (poręczenie, weksel własny,?sja wierzytelno
więcej podobnych podstron