6. Informacja merytoryczna

 

6.1. Podstawy fizyczne odkształceń plastycznych metali

 

6.1.1. Mechanizm odkształceń plastycznych

 

Rozróżnia się (między innymi) dwa podstawowe mechanizmy odkształceń plastycznych monokryształu: poślizg i bliźniakowanie. Poślizg zachodzi w określonych płaszczyznach
i kierunkach krystalograficznych o najgęstszym ułożeniu atomów. Wymaga on pewnej krytycznej wartości naprężenia stycznego _kr. Naprężenie to, obliczone przy założeniu sztywnego poślizgu całej warstwy atomów (tak zwany model Frenkla) jest rzędu G/2 * gdzie G jest modułem Kirchhoffa. Jest to wartość bardzo duża. W rzeczywistości poślizg zachodzi przy naprężeniach kilka tysięcy razy mniejszych wskutek ruchu dyslokacji. Poziom naprężeń potrzebny do spo-wodowania ruchu dyslokacji, decydujący o własnościach wytrzymałościowych zależy od wielu czynników. Głównymi przeszkodami w ruchu dyslokacji są różnego rodzaju defekty sieci krystalograficznej, a więc również inne dyslokacje.

Mechanizm odkształceń plastycznych materiału polikrystalicznego jest złożony wskutek występowania granic ziaren i zróżnicowania kierunków krystalograficznych
w poszczególnych krystalitach. Monokryształ może odkształcać się swobodnie, zgodnie
z uruchomionym systemem poślizgu. W ciele polikrystalicznym natomiast poszczególne ziarna muszą zmieniać swój kształt zgodnie z narzuconym stanem odkształcenia przy zachowaniu spójności na granicach. Wymaga to uruchomienia co najmniej kilku systemów poślizgu. Odkształcenia plastyczne nie pojawiają się we wszystkich ziarnach od razu. Pierwsze poślizgi wystąpią w tych ziarnach, które mają korzystną orientację płaszczyzn łatwego poślizgu względem obciążeń zewnętrznych. Dobre własności plastyczne wykazują więc metale, których sieci krystalograficzne mają wiele systemów poślizgu (rsc, rpc).

W miarę wzrostu odkształcenia ziarna wydłużają się zgodnie z kierunkiem największe-go odkształcenia. Równocześnie sieć krystalograficzna doznaje obrotu. W efekcie następuje pewne uporządkowanie (w sensie statystycznym) kierunków krystalograficznych w poszczególnych ziarnach, co nazywamy teksturą. Pojawienie się tekstury w materiale polikrystalicznym jest przyczyną anizotropii własności.

 

6.1.2. Zgniot i rekrystalizacja

 

Odkształcenia plastyczne wywołują szereg istotnych zmian we własnościach metali. Całokształt zmian własności fizycznych i mechanicznych spowodowanych przez odkształcenie plastyczne na zimno (poniżej temperatury rekrystalizacji) nazywamy zgniotem.

Stan zgniotu charakteryzuje się wzrostem własności wytrzymałościowych (granic sprężystości i plastyczności, wytrzymałości na rozciąganie, twardości itp.) oraz spadkiem własności plastycznych (wydłużenia, przewężenia, udarności).

 

Praca odkształcenia nie ulega dyssypacji cieplnej w całości. Pewna jej część (ok. 2 - 10%) zostaje zmagazynowana w postaci energii potencjalnej odkształceń sprężystych - wychyleń atomów z położeń równowagi wokół różnego rodzaju defektów sieci. Wartość energii zmagazynowanej zależy od gęstości dyslokacji, gdyż ten typ defektów występuje względnie często. Wynika stąd, że stan zgniotu jest termodynamicznie niestabilny. Występuje naturalna tendencja do obniżenia poziomu energii, co zachodzi w procesach zdrowienia, rekrystalizacji lub starzenia - zwłaszcza w podwyższonych temperaturach. Podczas zdrowienia znika część defektów punktowych (w drodze obsadzania wakansów przez dyfundujące atomy). Pewna ilość dyslokacji o przeciwnych znakach ulega anihilacji, pozostałe tworzą układy o niższej energii (np. granice wąskokątowe) - jest to tak zwana poligonizacja. W czasie zdrowienia zanikają naprężenia wewnętrzne, a własności materiału ulegają niewielkim zmianom - obniżają się nieco własności wytrzymałościowe i wzrastają plastyczne. Zakres tych zmian zależy od czasu
i temperatury.

 

Proces rekrystalizacji wymaga wyższych temperatur niż zdrowienie. Zachodzą tu istotne zmiany struktury, a zwłaszcza zarodkowanie i wzrost nowych ziaren. Wymagana tempera-tura rekrystalizacji zależy od poziomu energii zmagazynowanej - a tym samym od stopnia od-kształcenia plastycznego. Maleje ona wraz ze wzrostem odkształceń, dążąc do pewnej wartości granicznej, zwanej minimalną temperaturą rekrystalizacji. Minimalna temperatura rekrystalizacji powoduje przerekrystalizowanie materiału silnie odkształconego w określonym czasie (np. 1 godz.). Wynosi ona (dla czystych metali) ok. (0,4 - 0,5)T_top, gdzie T_top oznacza temperaturę topnienia (w stopniach Kelvina). Przy małych odkształceniach poziom energii zmagazynowanej jest niski i proces rekrystalizacji wymaga wyższych temperatur (i większego czasu).

Podczas rekrystalizacji materiał odzyskuje utracone własności plastyczne, obniżeniu ulegają natomiast własności wytrzymałościowe.

 

Rozróżnia się rekrystalizację pierwotną oraz wtórną, podczas której następuje rozrost ziaren. Wielkość ziarna po rekrystalizacji zależy od wielkości ziarna początkowego, temperatury i czasu wyżarzania oraz stopnia odkształcenia. Korzystne z wielu względów jest uzyska-nie drobnoziarnistej i jednorodnej struktury. Sprzyjają temu duże i jednorodne odkształcenia plastyczne. Maksymalne wymiary ziarna otrzymuje się dla tak zwanego „gniotu krytycznego”, który oznacza wartość odkształcenia w mierze Cauchy'ego rzędu 2 - 10 %
(w zależności od rodzaju materiału).

 

6.1.3. Dyslokacyjny mechanizm wzmocnienia.

 

Wzrost własności wytrzymałościowych materiału nazywamy wzmocnieniem. Jest ono spowodowane wzrostem poziomu naprężeń potrzebnych do przemieszczania dyslokacji.

 

Głównym powodem wzmocnienia zachodzącego w trakcie odkształceń plastycznych na zimno (tak zwane wzmocnienie odkształceniowe) jest wzrost gęstości dyslokacji, który przebiega zgodnie z zależnością:

 

ρρ₀*B^a (I.1)

 

gdzie: ρ₀ - początkowa gęstość dyslokacji [mm^-1],  - odkształcenie, a, B - współczynniki zależne od rodzaju materiału.

 

Zwiększająca się podczas odkształceń plastycznych gęstość dyslokacji powoduje utrudnienie ich ruchu i wzrost naprężeń.

 

W rzeczywistości dyslokacyjny mechanizm wzmocnienia jest bardzo złożony. Występu-je wpływ zanieczyszczeń i granic ziaren. Zjawisko wzmocnienia może być do pewnego stopnia modyfikowane przez istniejący stan naprężenia. Obecność naprężeń ściskających sprzyja powstawaniu nowych granic ziaren z układów dyslokacji. Naprężenia rozciągające prowadzą do zarodkowania szczelin i naruszenia spójności.

 

Wzmocnienie trwa tak długo, jak długo wzrasta gęstość dyslokacji. Zjawisko wykazuje pewne nasycenie - w miarę wzrostu odkształcenia gęstość dyslokacji wzrasta coraz wolniej. Dlatego szybkość wzrostu naprężenia uplastyczniającego jest początkowo duża i maleje wraz ze wzrostem odkształceń.

 

Rozkład gęstości dyslokacji w objętości odkształcanego materiału nie jest jedno-rodny. W ziarnach powstaje substruktura komórkowa, przy czym ściany komórek cechuje gęstość dyslokacji kilkakrotnie większa od średniej. Przy dalszym wzroście odkształceń ze splotów dyslokacji powstają nowe granice ziaren. Tworzy się tak zwana struktura ziarenkowa o średnim wymiarze ziarenek rzędu 1 m. Tak zaawansowany proces odkształceń, możliwy tylko w obecności dużych ujemnych wartości naprężenia średniego (inaczej wcześniej nastąpi naruszenie spójności materiału), nie wywołuje już dalszego wzmocnienia.

 

Uwaga. Informacja podana w p. 6.1 została opracowana w formie skróconej. Bardziej szczegółowy opis zjawisk fizycznych towarzyszących odkształceniom plastycznym można znaleźć w literaturze [1-3,5-7].

 

6.2. Fenomenologiczny opis wzmocnienia

 

6.2.1. Wzmocnienie izotropowe i kinematyczne

 

Każdy warunek plastyczności przedstawia w dziewięciowymiarowej przestrzeni naprężeń tak zwaną powierzchnię plastyczności. Stan naprężenia reprezentowany jest w tej przestrzeni wektorem  o składowych σ_ij. Jeżeli koniec tego wektora *leży na powierzchni plastyczności, to materiał jest w stanie plastycznym, jeżeli wewnątrz - w stanie sprężystym (lub sztywnym, gdy pomija się odkształcenia sprężyste). Nie można osiągnąć stanu, dla którego koniec wektora  znajduje się na zewnątrz powierzchni plastyczności (rys. I/2). Dla materiału nie wykazującego wzmocnienia powierzchnia plastyczności nie ulega zmianom. W dalszym ciągu przyjmiemy model materiału sztywno - plastycznego, co przy dużych odkształceniach występujących w procesach obróbki plastycznej jest w pełni uzasadnione.

 

 

 

 

 

 

 

 

 

 

 

 

 

Rys. I/2. Schemat powierzchni plastyczności w przestrzeni naprężeń

Opis wzmocnienia wymaga przyjęcia pewnych założeń, określających charakter zmian powierzchni plastyczności podczas plastycznego płynięcia. Najczęściej korzysta się z dwóch podanych w dalszym ciągu hipotez.

 

Hipoteza wzmocnienia izotropowego zakłada zwiększanie się wymiarów powierzchni plastyczności z zachowaniem podobieństwa geometrycznego. Warunek plastyczności Hubera-Misesa przyjmuje postać:

(I.2)

 

gdzie
jest drugim niezmiennikiem dewiatora naprężeń:

 

(I.3)

 

(przez S_ij oznaczono składowe dewiatora naprężenia). Związek (I.2) we współrzędnych kartezjańskich (i, j = x, y, z) można zapisać w postaci:

 

(I.4)

 

lub, gdy znane są wartości naprężeń głównych σ₁, σ₂ i σ₃

 

(I.5)

 

Naprężenie uplastyczniające σ_p jest funkcją parametru wzmocnienia , którego określenie jest związane z pracą właściwą (na jednostkę objętości) odkształceń plastycznych.

 

Hipoteza wzmocnienia kinematycznego zakłada translację powierzchni plastyczności bez zmiany jej wymiarów, co daje następującą postać warunku plastyczności:

 

(I.6)

 

gdzie _ij jest tensorem zależnym od odkształceń plastycznych, σ₀ oznacza stałą wartość naprężenia uplastyczniającego. Dla wzmocnienia liniowego:

 

(I.7)

 

gdzie c jest stałym współczynnikiem. Hipoteza wzmocnienia kinematycznego uwzględnia efekt Bauschingera polegający na tym, że po odciążeniu i ponownym obciążeniu naprężeniami o znaku przeciwnym ponowne uplastycznienie następuje przy mniejszych (co do bezwzględnej wartości) naprężeniach, niż to wynika z hipotezy wzmocnienia izotropowego.

Widoczne jest, że możliwa jest następująca modyfikacja warunku (I.6):

 

(I.8)

 

która uwzględnia jednocześnie translację oraz izotropowe zwiększenie wymiarów powierzchni plastyczności.

 

Na rys. I/3 przedstawiono schematycznie przebieg zmian elipsy plastyczności Hubera-Misesa w przestrzeni naprężeń głównych σ₁, σ₂ (płaski stan naprężenia, warunek (I.5) po podstawieniu σ₃ = 0) dla omawianych hipotez wzmocnienia.

W modelowaniu procesów obróbki plastycznej, gdy wektor  zmienia kierunek w niewielkim stopniu, można korzystać z hipotezy wzmocnienia izotropowego.

 

Rys. I/3. Schemat przebiegu zmian elipsy plastyczności Hubera - Misesa w przestrzeni naprę-żeń głównych σ₁, σ₂ (płaski stan naprężenia) dla różnych hipotez wzmocnienia: a) wzmocnienie izotropowe, b) wzmocnienie kinematyczne przy jednoosiowym rozciąganiu naprężeniem σ₁, c) wykres zależności σ_p() przy jednoosiowym rozciąganiu i następnie ściskaniu dla materiału wykazującego efekt Bauschingera (linia 1); linia 2 przedstawia przebieg zmian σ_p podczas ściskania przy braku efektu Bauschingera

6.2.2. Prawo plastycznego płynięcia przy wzmocnieniu izotropowym. Odkształcenie zastępcze

Niech d_ij oznacza składowe tensora przyrostu odkształceń plastycznych. Przyjmując, że wektor d o składowych d_ij jest w przestrzeni naprężeń ortogonalny do aktualnej po-wierzchni plastyczności (rys. I/2) otrzymuje się tzw. stowarzyszone prawo plastycznego płynięcia:

 

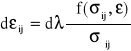
(I.9)

 

gdzie d jest dodatnio określonym mnożnikiem. Różniczkując (I.2) otrzymujemy:

 

(I.10)

 

Wykorzystując (I.2), (I.3) i (I.10) można wyrugować mnożnik d* Prawo płynięcia przyjmuje postać:

 

(I.11)

 

Przyrost pracy właściwej (na jednostkę objętości) podczas odkształcenia plastycznego dla materiału nieściśliwego (d_kk = 0) wyraża się wzorem:

 

(I.12)

 

gdzie wykorzystano (I.2) i (I.11). Przyrost parametru wzmocnienia (odkształcenia zastępczego) d definiuje się za pomocą związku:

 

(I.13)

 

Ostatecznie po wykorzystaniu (I.12) otrzymujemy:

 

(I.14)

 

Przyrost odkształcenia zastępczego d *jest związany z drugim niezmiennikiem dewiatora przyrostu odkształcenia plastycznego
za pomocą zależności:

 

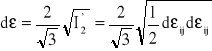
(I.15)

 

która obowiązuje dla materiału nieściśliwego (gdy d_kk = 0).

 

Wykorzystując (I.14) i (I.11) otrzymuje się ostateczną postać prawa płynięcia stowarzyszonego z warunkiem plastyczności (I.2) dla materiału sztywno - plastycznego ze wzmocnieniem izotropowym:

 

(I.16)

 

Wartość odkształcenia zastępczego wyznacza się w drodze całkowania:

 

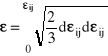
(I.17)

 

Odkształcenie zastępcze nosi także nazwę intensywności odkształceń i bywa definiowane z innymi niż w (I.17) współczynnikami liczbowymi.

Związek (I.14) we współrzędnych kartezjańskich (i, j = x, y, z) można zapisać w postaci:

 

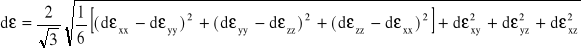
(I.18)

 

lub, gdy znane są wartości główne d_1 * d₂ i d₃:

 

(I.19)

 

Związek (I.19) wynika z (I.14) po podstawieniu: d_xx = d₁, d_yy = d₂, d_zz = d₃, d_xy = d_yz = d_xz = 0.

 

6.2.3. Naprężenie uplastyczniające i krzywa wzmocnienia

 

W jednorodnych i jednoosiowych stanach naprężenia naprężenie uplastyczniające σ_p jest naprężeniem rzeczywistym, określanym jako stosunek siły do przekroju aktualnego próbki w zakresie plastycznym, co można łatwo sprawdzić stosując (I.4). Nie jest to wartość stała (w odróżnieniu np. od umownej granicy plastyczności R_{e 0,2}), lecz pewna funkcja, zależna od odkształceń plastycznych, temperatury i prędkości odkształcenia. Funkcja ta nie jest jedno-znaczna, gdyż naprężenie uplastyczniające zależy nie tylko od chwilowych wartości tych para-metrów, lecz również od historii ich zmian. Jest to związane z ewolucją struktury materiału pod wpływem działania odkształceń plastycznych i temperatury (np. średni wymiar ziarna ulega zmianie).

 

W dowolnym stanie naprężenia aktualną wartość σ_p oblicza się z (I.4) lub (I.5). Muszą być znane wszystkie składowe tensora σ_ij, względnie wartości naprężeń głównych σ_, σ_ i σ₃ (na podstawie znanego obciążenia).

 

Krzywa wzmocnienia przedstawia zależność naprężenia uplastyczniającego σ_p od odkształcenia zastępczego  *w stanie plastycznym przy ustalonej temperaturze T i składowych tensora prędkości odkształcenia e_ij:

 

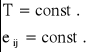
(I.20)

 

Przy wzmocnieniu izotropowym funkcja (I.20) jest niezależna od stanu naprężenia, co zostało potwierdzone doświadczalnie (por. [1], s. 59).

 

6.3. Doświadczalna identyfikacja krzywej wzmocnienia

 

6.3.1. Metody badawcze

 

Teoretyczne wyznaczenie krzywej wzmocnienia (na podstawie teorii dyslokacji i znajomości aktualnych parametrów mikrostruktury) napotyka duże trudności. W związku z tym funkcję tę identyfikuje się doświadczalnie różnymi metodami. Najczęściej stosuje się próby:

 rozciągania,

 ściskania w warunkach zbliżonych do braku tarcia,

 skręcania krążka blachy w jego płaszczyźnie lub tulejki cienkościennej.

6.3.2. Próba rozciągania

 

Podstawą do wyznaczenia krzywej wzmocnienia jest otrzymana zależność siły od wy-dłużenia próbki (rys. I/4). Współrzędne P - l można przeliczyć na wartości σ_p -  tylko dla punktów pomiędzy 1 i 2 (zakres odkształceń równomiernych).

 

Rys. I/4. Wykres rozciągania (a) i odpowiednia krzywa wzmocnienia (b)

Przykładowo dla p. A:

 

(I.21)

gdzie przez F₀ i F oznaczono odpowiednio: początkowy i aktualny przekrój próbki, l₀ jest długością początkową odcinka pomiarowego próbki, a l_c - odpowiednim wydłużeniem. Odkształcenie zastępcze wyznacza się, biorąc pod uwagę panujący stan odkształcenia:

 

(I.22)

 

Wykorzystując (I.19) i (I.22) otrzymujemy:

 

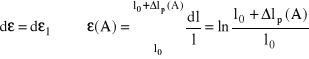
(I.23)

Wadą opisanego sposobu jest mały zakres odkształceń równomiernych, możliwych do realizacji w próbie rozciągania.

 

6.3.3. Próba ściskania w warunkach zbliżonych do braku tarcia

 

W celu eliminacji tarcia wykonuje się specjalne próbki z wybraniami na powierzchniach czołowych, stykających się z kowadłami (rys. I/1). Wybrania te wypełnia się smarem. Można również stosować zwykłe próbki walcowe, oddzielając je od kowadeł przekładkami z cienkiej folii teflonowej. W czasie ściskania próbki zachowują w części środkowej kształt walcowy
i można przyjąć, że w tej strefie stan naprężenia jest jednorodny i jednoosiowy. Podczas próby mierzy się siłę P i aktualną średnicę d. Wartości σ_p wyrażają się wzorem:

 

(I.24)

 

Bieżące wartości odkształcenia zastępczego wyznacza się, uwzględniając panujący stan od-kształcenia:

 

(I.25)

 

Biorąc pod uwagę (I.19) i (I.25) oraz warunek stałej objętości: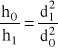
otrzymujemy:

 

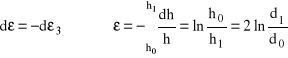
(I.26)

 

Możliwe jest wyznaczenie krzywej wzmocnienia dla dużych odkształceń.

 

6.3.4. Próby skręcania

 

Stosuje się dwa rodzaje prób skręcania. Pierwsza z nich polega na skręcaniu krążka z blachy, utwierdzonego w pobliżu środka oraz na obwodzie w uchwytach specjalnego przy-rządu. Po naniesieniu na powierzchni krążka linii prostych wzdłuż promieni powoduje się obrót uchwytów względem siebie o pewien kąt i mierzy wartość momentu skręcającego M_s. Stan odkształcenia wyznacza się, badając deformację wyrysowanych linii promieniowych (patrz rys. I/5 a).

 

Rys. I/5. Schematy prób skręcania: a) krążka blachy, b) tulejki cienkościennej

Wartości σ_p i  * wyznacza się jak następuje. Warunek równowagi płaskiego krążka o stałej grubości g obciążonego tylko naprężeniami stycznymi σ_r ma postać:

 

(I.27)

 

Całkowanie równania (I.27) przy warunku brzegowym:

 

(I.28)

 

gdzie R jest zewnętrznym promieniem krążka, daje:

 

(I.29)

 

Wykorzystując (I.4) i (I.29) otrzymuje się:

 

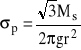
(I.30)

 

Tensor przyrostu odkształcenia ma tylko jedną niezerową składową d_r* którą można wyrazić przez kąt γ (rys. I/5 a). Po scałkowaniu (I.18):

 

(I.31)

 

Kąt γ mierzy się jak na *rys. I/5 a. Można badać deformację pojedynczej linii, mierząc kąt γ dla różnych promieni r (przy ustalonej wartości momentu M_s), lub zmieniać moment skręcający i mierzyć kąt γ w tym samym miejscu (ustalony promień r). Możliwy jest większy zakres od-kształceń niż przy rozciąganiu.

 

Drugi sposób polega na skręcaniu tulejki cienkościennej (rys. I/5 b) i rejestracji momentu M_s w funkcji kąta skręcenia . Odpowiednie wartości σ_p i  wyznacza się ze wzorów:

 

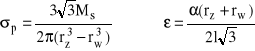
(I.32)

 

gdzie: r_z, r_w - promienie (odpowiednio: zewnętrzny i wewnętrzny) skręcanej tulejki, l - długość odcinka pomiarowego,  - kąt skręcenia.

 

6.4. Aproksymacja krzywej wzmocnienia

 

Krzywą wzmocnienia dogodnie jest aproksymować funkcjami potęgowymi typu:

 

(I.33)

(I.34)

(I.35)

 

które dobrze oddają charakter zjawiska. Ten sam typ równania opisuje wiele materiałów, zmia-nie ulegają jedynie współczynniki n, n₁, ₀, n₂, C, C₁, C₂ i C₃. Aproksymację można prze-prowadzić, wykorzystując odpowiednie programy komputerowe. Funkcja (I.34), gdy ₀ < 0, nie jest odpowiednia dla małych odkształceń plastycznych. Przykłady konkretnych funkcji aproksymujących typu (I.33) - (I.35) dla różnych materiałów można znaleźć między innymi w [1].

 

6.5. Znaczenie i wykorzystanie krzywej wzmocnienia

 

Znajomość przebiegu krzywej wzmocnienia jest niezbędna przy modelowaniu proce-sów obróbki plastycznej z uwzględnieniem wzmocnienia oraz pozwala na przewidywanie włas-ności materiału odkształconego.

 

Zgodnie z (I.13) pracę odkształcenia plastycznego dla materiału nieściśliwego przy izotropowym wzmocnieniu można wyrazić następująco:

 

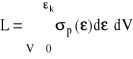
(I.36)

 

Jeżeli w objętości V obszaru uplastycznionego panuje jednorodny stan odkształcenia, to:

 

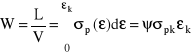
(I.37)

 

gdzie: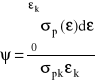

(I.38)

 

jest współczynnikiem wypełnienia wykresu krzywej wzmocnienia. Przez σ_pk i _k oznaczono odpowiednio końcowe wartości naprężenia uplastyczniającego i odkształcenia zastępczego. Jak widać z (I.37) praca właściwa W jest równa polu pod wykresem krzywej wzmocnienia (rys. I/4 b).

W celu przybliżonego wyznaczenia sił w procesach obróbki plastycznej można wykorzystać metodę energetyczną, polegającą na porównaniu pracy sił zewnętrznych L_z z pracą całkowitą L_c niezbędną do realizacji procesu:

 

(I.39)

gdzie: L_t - praca wykonana przeciwko siłom tarcia,  - współczynnik sprawności procesu.

Przykładowo dla procesów ciągnienia i wyciskania współbieżnego (rys. I/6):

 

Rys. I/6. Schematy procesów: a) ciągnienia, b) wyciskania współbieżnego;

1 - materiał kształtowany, 2 - stempel, 3 - matryca, 4 - ciągadło

(I.40)

 

Przy założeniu jednorodności stan odkształcenia jest taki sam jak w jednoosiowych stanach naprężenia, a więc odkształcenie zastępcze można wyznaczyć ze stosunku przekrojów:

 

(I.41)

Wzory (I.23), (I.26) i (I.41) są równoważne, gdyż materiał nie zmienia objętości. Ponieważ przy wyciskaniu współbieżnym V = F₀l, a przy ciągnieniu V = F_kl, więc po wykorzystaniu (I.37), (I.40) i (I.41) otrzymujemy następujące wzory przybliżone:

- dla wyciskania współbieżnego:

 

(I.42)

 

- dla ciągnienia (bez przeciwciągu):

 

(I.43)

Współczynnik ၹ dla konkretnej funkcji aproksymującej krzywą wzmocnienia może być obliczony i tablicowany na podstawie wzorów (I.38) i (I.33) - (I/35) jako funkcja _k. Dla (I.33) otrzymuje się:

 

(I.44)

 

Współczynnik  *zależy głównie od współczynnika tarcia, kąta matrycy lub stożka roboczego ciągadła  i stopnia odkształcenia (dla wyciskania również od stosunku wysokości wstępniaka do jego średnicy) i przyjmuje wartości rzędu 0,5 - 0,8. Spełnia on rolę współczynnika korygującego przyjęte założenia upraszczające.

 

 

6.6. Czynniki wpływające na naprężenie uplastyczniające

 

Jak już powiedziano (p. 6.2.3), naprężenie uplastyczniające zależy od odkształcenia, prędkości odkształcenia i temperatury. Występuje wpływ parametrów charakteryzujących strukturę materiału (średnia wielkość ziarna, skład fazowy i morfologia faz, obecność zanieczyszczeń itp.). Przykładowo wpływ średniego wymiaru ziarna d opisuje równanie Halla-Petcha:

 

(I.45)

 

gdzie A i B są stałymi współczynnikami. Stosowanie odkształceń plastycznych na zimno nie jest jedynym sposobem wzmacniania materiałów. Oprócz granic ziarn przeszkodą dla ruchu dyslokacji mogą być atomy obce lub drobne wydzielenia, co jest wykorzystywane do wzmacniania materiałów w operacjach obróbki cieplnej i cieplno - chemicznej (np. przez tworzenie stopów oraz utwardzanie dyspersyjne).

 

Wpływ wyżej wymienionych czynników jest skomplikowany i wzajemnie powiązany. Nie można ustalić jednoznacznej funkcji obejmującej wpływ wszystkich czynników.

 

6.6.1. Wpływ prędkości odkształcenia

 

Dla większości materiałów naprężenie uplastyczniające wzrasta wraz z prędkością od-kształcenia. Cecha ta może być opisana w ramach modelu lepkoplastycznego [4], który pozwala na równoczesne uwzględnienie wzmocnienia (kinematycznego lub izotropowego) oraz wrażliwości na prędkość odkształcenia. Model ten przewiduje dodatkowe izotropowe powiększenie wymiarów powierzchni plastyczności, wywołane wpływem prędkości odkształcenia. Przy pewnych dodatkowych założeniach tak zwaną dynamiczną krzywą wzmocnienia można opisać równaniem:

 

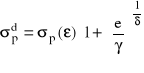
(I.46)

 

gdzie e jest intensywnością prędkości odkształcenia, która wyraża się przez składowe tensora prędkości odkształcenia e_ij jak następuje:

 

(I.47)

 

Współczynniki: γ (o wymiarze s^-1) i δ charakteryzują zachowanie się materiału wrażliwego na prędkość odkształcenia. Dla większości metali istotny wpływ prędkości odkształcenia występuje wyłącznie w podwyższonych temperaturach i wysokich prędkościach (gdy e jest rzędu 10² s^-1). Inny sposób opisu wpływu prędkości odkształcenia można znaleźć w [1].

 

6.6.2. Wpływ temperatury

 

Podwyższenie temperatury powoduje wyraźny spadek naprężenia uplastyczniającego, gdyż dzięki drganiom cieplnym występuje zwiększona ruchliwość dyslokacji. Ponadto mogą zachodzić dynamiczne procesy zdrowienia i rekrystalizacji. Materiał odkształcany na gorąco z małą prędkością prawie nie wykazuje wzmocnienia. Obniżenie temperatury powoduje podobne skutki jak podwyższenie prędkości odkształcenia. Należy dodać, że parametry te wpływają również na własności plastyczne. Materiały odkształcane z dużą prędkością lub w niskich temperaturach wykazują mniejszą zdolność do odkształceń plastycznych i skłonność do kruchego pękania (zwłaszcza w obecności naprężeń rozciągających).

Spadek naprężenia uplastyczniającego w miarę wzrostu temperatury nie dla wszystkich stopów metali przebiega monotonicznie. W pewnych zakresach temperatur mogą wystąpić lokalne maksima, spowodowane wydzielaniem się nowej fazy (np. w stalach występuje tzw. kruchość na niebiesko, spowodowana zjawiskiem dynamicznego starzenia odkształceniowego w temperaturach rzędu 300 - 500 ^oC).

Uwzględnienie wpływu temperatury polega zwykle na wprowadzeniu zamiast krzywej wzmocnienia doświadczalnej zależności σ_p = σ_p(T) w postaci wielomianu lub funkcji wykładniczej (w przypadku obróbki plastycznej na gorąco wzmocnienie można pominąć). Przykład takiej zależności podano na rys. I/7.

 

σ_p [MPa]

t [^oC]

Rys. I/7. Zależność naprężenia uplastyczniającego od temperatury ( = 0,15,
) dla stali 45 [8]

7. Literatura

 

1. S. Erbel, K. Kuczyński, Z. Marciniak: Obróbka plastyczna. PWN, Warszawa 1981

2. Z. Gabryszewski, J. Gronostajski: Mechanika procesów obróbki plastycznej. PWN, Warszawa 1991

3. M. Morawiecki, L. Sadok, E. Wosiek: Przeróbka plastyczna. Podstawy teoretyczne. Wyd. "Śląsk", Katowice 1977

4. P. Perzyna: Teoria lepkoplastyczności. PWN, Warszawa 1966

5. S. Rudnik: Metaloznawstwo. Skrypt dla studentów wyższych szkół technicznych do przedmiotu: Materiałoznawstwo. Politechnika Krakowska, Kraków 1979

6. W. Szczepiński: Wstęp do analizy procesów obróbki plastycznej. PWN, Warszawa 1967

7. O. H. Wyatt, D. Dew-Hughes: Wprowadzenie do inżynierii materiałowej. WNT, War-szawa 1978

8. Z. Marciniak: Problemy badawcze związane z obróbką plastyczną na ciepło. Obróbka plastyczna 5, 1990

Przy jednoosiowym rozciąganiu lub ściskaniu w kierunku osi x mamy: σ_xx
0, pozostałe składowe tensora naprężenia są zerami. Zatem σ_p = ၼσ_xxၼ.

dE(d_ij)

(σ_ij)

Stan sprężysty

(lub sztywny)

Stan plastyczny

2

1

1

σ_ps

σ_pr

σ_p

σ_p2

σ₂

σ₁

σ₂

σ_pr

ၥ =

σ_p

σ_p1

σ₀

σ₁

ၥ₁

ၥ₂

σ_ps

σ₀

a)

b)

c)

P

a)

ၥ

ၥ(A)

B'

A'

2'

1'

σ_p(A)

σ_p

2

l_c (A)

l_p (A)

B

A

1

l

P(A)

b)

M_s

ၧ

r

M_s

a)

b)

l

P

2

a)

F₀

F_k

1

4

l

2

3

1

P

F₀

F_k

b)

---