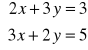
Temat: Rozwiązywanie układów równań przy pomocy narzędzia SOLVER i algebry macierzy.

Zadanie 1. (Arkusz 1). Rozwiązanie układu dwóch równań liniowych przy użyciu narzędzia SOLVER.

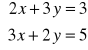
W celu rozwiązania układu równań należy stworzyć arkusz (rysunek 1)
i wprowadzić następujące formuły:

• F8: =C8*B8+D8*B9+E8 Pierwsze równanie układu

• F9: =C9*B8+D9*B9+E9 Drugie równanie układu

• G8: =MODUŁ.LICZBY(f8)

• G9: =MODUŁ.LICZBY(f9)

• G10: =G8+G9

Uruchamiamy Solver, jako Komórkę celu wyznaczamy G10 natomiast Komórki zmienne to B8:B9. Wartość 0.

Zadanie 2 - Arkusz 2

1. Utwórz następujące macierze:

	A	B
1	MACIERZ A
2	4	12
3	-8	7

	D	E
1	MACIERZ B
2	-3	-6
3	-1	9

	G	H
5	MACIERZ D
6	1	-2
7	8	4

2. Utwórz:

• MACIERZ C, która będzie sumą MACIERZY B i A

	G	H
1	MACIERZ C
2
3

• MACIERZ D^-1, która będzie macierzą odwrotną do MACIERZY D. W tym celu utwórz tabelkę:

	D	E
5	MACIERZ D^-1
6
7

a następnie wpisz w komórkę D6 formułę: =MACIERZ.ODW(G6:H7); zaznacz zakres D6:E7 (począwszy od komórki formuły), naciśnij klawisz F2, a następnie klawisze CTRL+SHIFT+ENTER.

• MACIERZ DxD^-1, według poprzedniego podpunktu, jednak tu formuła przyjmie postać: =MACIERZ.ILOCZYN(G6:H7;D6:E7) (gdy G6:H7 jest w tym przykładzie MACIERZĄ D, zaś D6:E7 jest MACIERZĄ D^-1)

• WYZNACZNIK MACIERZY D:

	A	B
9	WYZNACZNIK
10

w komórce A10 należy wpisać formułę =WYZNACZNIK.MACIERZY(G6:H7), zaś w komórce B10 formułę, która wyświetlałaby informację, że MACIERZ D jest osobliwa, gdy jej wyznacznik jest równy zero, a w pozostałych przypadkach jest ona nieosobliwa (=JEŻELI(A12=0;"OSOBLIWA";"NIEOSOBLIWA")).

Zadanie 3 - Arkusz 3

Rozwiąż układ równań:

x - y + z - w = -1

4x - y + 3z + 2w = 8

x + 4y - z + 8w = -4

2x - y + z + 3w = 10

W tym celu utwórz:

• MACIERZ WSPÓŁCZYNNIKÓW (A), w której w czterech kolumnach znajdą się odpowiednio współczynniki liczbowe przy niewiadomych x, y, z, w

	A	B	C	D
8	MACIERZ WSPÓŁCZYNNIKÓW (A)
9	1	-1	1	-1
10	4	-1	3	2
11	1	4	-1	8
12	2	-1	1	3

• MACIERZ STAŁYCH (B), w której w jednej kolumnie znajdą się liczby z prawych stron równań

	F
7	MACIERZ
8	STAŁYCH (B)
9	-1
10	8
11	-4
12	10

• WYZNACZNIK MACIERZY A (jak w Zadaniu 1) - w komórce I9

• MACIERZ ODWROTNĄ (A^-1) (wpisz formułę, która wyświetlałaby informację, że MACIERZ A jest osobliwa, gdy jej wyznacznik jest równy zero, a w przeciwnym wypadku wstawiałaby MACIERZ ODWROTNĄ - =JEŻELI(I9=0;"OSOBL.";MACIERZ.ODW(A9:D12)))

• MACIERZ ROZWIĄZAŃ A^-1xB=X

	F	G
14	A^-1xB=X
15	x
16	y
17	z
18	w

w komórkę G15 wpisz formułę, która wyświetlałaby informację, że MACIERZ A jest osobliwa, gdy jej wyznacznik jest równy zero, a w przeciwnym wypadku wstawiałaby iloczyn MACIERZY A^-1 i B - =JEŻELI(I9=0;"OSOBL.";MACIERZ.ILOCZYN(A15:D18;F9:F12)) - A15:D18 MACIERZ ODWROTNA).

Zadanie 3 - Arkusz 3

Rozwiąż równanie 3. stopnia (w następującej postaci:
) przy pomocy narzędzia Szukaj wyniku.

W tym celu utwórz tabelkę:

	A	B	C	D
1	Rozwiązywanie równań trzeciego stopnia
2	Współczynniki		Pierwiastki	Funkcja
3	a=	3
4	b=	14
5	c=	-356
6	d=	6

współczynniki a, b, c, d mogą być takimi lub podobnymi liczbami.

• zaadresuj komórki, w których znajdują się wartości współczynników (B3, B4, B5, B6), aby później móc odwoływać się do nich bez wpisywania adresu: Wstaw - Nazwa - Definiuj

• utwórz wykres (XY (punktowy) - paraboliczny) funkcji trzeciego stopnia w zakresie od -15 do 15, wykorzystując w formule zaadresowanie komórek: =a*C3^3+b*C3^2+c*C3+d; funkcja 3. stopnia może mieć od 0 do 3 pierwiastków

• następnie, będąc w komórce kolumny Funkcja wejdź: Narzędzia - Szukaj wyniku; w Ustaw komórkę ma być wpisany adres komórki z kolumny Funkcja (D3), w Wartość ma być wpisana liczba zero, w Zmieniając komórkę ma być wpisany adres komórki z kolumny Pierwiastek (C3); to narzędzie znajduje wynik (pierwiastek równania) najbliższy wpisanej przez nas liczbie (lecz niech liczby w kolumnie Pierwiastek nie będą dowolne, ale odczytane „mniej więcej” na podstawie utworzonego wykresu).

Laboratorium Podstaw Informatyki 2.3

---