Sprawozdanie z ćwiczenia nr A-23

Temat:Wyznaczanie odległości międzypłaszczyznowych metodą odbicia Bragga.

Podstawy teoretyczne.

Kryształ - jest to substancja, której budowa wewnętrzna wykazuje wysoki stopień uporządkowania przestrzennego, ponieważ można znaleźć najmniejszy element jego struktury - komórką elementarną - taki, że przez proste przesunięcia dane poniższym wzorem można odtworzyć całą strukturę :

gdzie: R - promień wodzący dowolnego punktu w komórce elementarnej,

r - promień wodzący równoważnego mu punktu w innej komórce,

n1, n2, n3 - liczby całkowite (0, 1, 2),

a, b, c - wektory bazowe sieci (wyznaczające jedną z komórek elementarnych).

Podstawowym zjawiskiem umożliwiającym badanie struktury kryształów jest dyfrakcja. Istnieje kilka metod badawczych:

- krystalografia rentgenowska wykorzystująca promienie rentgenowskie

- neutronografia realizowana poprzez rozpraszanie neutronów na krysztale

- elektronografia realizowana poprzez rozpraszanie elektronów, przyśpieszonych za

pomocą różnicy potencjałów rzędu 20-200 kV, co pozwala badać warstwy do grubości

100 nm. W krystalografii podstawową rolę odgrywa odbicie padającej wiązki promieniowania od płaszczyzn sieciowych kryształu - płaszczyzn na których leży część atomów kryształu - zwane odbiciem Bragga.

Dla ułatwienia odbicia Bragga wprowadzone zostało oznaczanie płaszczyzn sieciowych przy pomocy tzw wskaźników Millera.

Wskaźniki Millera (hkl) - wyznaczają rodzinę płaszczyzn sieciowych, które dzielą podstawowe jednostki sieciowe na odpowiedni h, k i l równych odcinków. W przypadku równoległości do którejś z osi, to odpowiadający jej wskaźnik przyjmujemy jako (0). Wskaźnik podaje się w nawiasach okrągłych, podzielony ewentualnie przez wspólny dzielnik.

Samo odbicie Bragga ma charakter interferencyjny, ponieważ - w przypadku promieniowania rentgenowskiego - powstaje w następujący sposób: elektrony atomu kryształu poruszając się zgodnie z wymuszającym ich ruch polem elektrycznym fali padającej, stają się źródłem promieniowania elektromagnetycznego o takiej samej częstości, lecz rozchodzącego się kuliście w przestrzeni; te wtórne fale interferują ze sobą, dając w pewnych kierunkach (ściśle wyznaczonych przez sieć przestrzenną, kierunek oraz długość fali promieniowania padającego) wzmocnienia - obserwowane jako wypadkowa fala odbita. Oczywiście fala leży w płaszczyźnie wyznaczonej przez kierunek fali padającej i normalną (prostą prostopadłą) do płaszczyzn sieciowych odbijających.

Jak wiemy wzmocnienie interferujących fal zachodzi wówczas, gdy różnica dróg optycznych przebytych przez te fale równa jest wielokrotności długości fali.

W przypadku odbić od płaszczyzn sieciowych warunek ten można wyrazić następującym

równaniem Wulfa- Bragga :

gdzie: n - rząd odbicia,

- długość fali promieniowania padającego,

d(hkl) - odległość między płaszczyznami odbijającymi,

- kąt padania (połysku) mierzony między kierunkiem fali padającej a płaszczyzną sieciową.

Obrazuje to konstrukcja jak na rysunku:

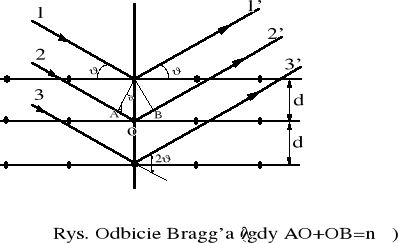
Z powyższego rysunku wynika, że wzmocnieni fali wypadkowej będącej superpozycją fal odbitych, nastąpi wtedy, gdy S będzie całkowitą wielokrotnością długości fali padającej . Dzięki temu, że różnice dróg między wiązkami odbitymi od dowolnych płaszczyzn wyrażają się jako całkowite wielokrotności S, uzyskujemy kolektywne wzmocnienie interferencyjne.

Wykonanie ćwiczenia.

1. Zestawiamy układ pomiarowy złożony z nadajnika fal mikrofalowych (zastępujące kłopotliwe w zastosowaniu w naszych warunkach promieniowanie rentgenowskie), o długości około 3 cm , detektora fal połączonego z miernikiem.

2. Ustawiamy kryształ o strukturze prostej rombowej, ukrytym w styropianowym sześcianie. Znajdujemy odbicie Bragga, zmieniając w tym celu orientację kryształu i detektora.

Sygnałem o znalezieniu odbicia Bragga jest maksymalne natężenie sygnału wyjściowego detektora.

Wówczas odczytujemy podwojony kąt odbicia - 2:

- 2=43 stąd =2130'

3. Wyznaczamy wartość długości promieniowania mikrofalowego ze wzoru:

d(hkl) - jest zmierzoną odległością między zaznaczonymi kreskami, wyznaczającymi określone płaszczyzny.

d(hkl) = 33,8 10-3 m

Po podstawieniu do wzoru otrzymujemy:

=25 10-3 m dla n=1 (rząd odbicia)

4. Zmieniamy model kryształu na kryształ o strukturze heksagonalnej o najgęstszym stopniu upakowania, wykonanym z polistyrenowych kulek. Dla tego kryształu znajdujemy odbicia Bragga, postępując jak w poprzednim przypadku. Pomiary wykonujemy dla dwóch ustawień w których udało nam się zaobserwować odbicia Bragga.

- pierwsze ustawienie:

2=48 stąd =24

Znając wyznaczoną wcześniej długość fali promieniowania mikrofalowego wyznaczamy

odległość międzypłaszczyznową d(hkl) za wzoru Wulfa-Bragga.

(dla n=1)

- drugie ustawienie :

2=56 stąd =28

Po podstawieniu otrzymujemy:

(dla n=1)

Dyskusja błędów.

1. Obliczamy błąd wyznaczenia długości fali promieniowania mikrofalowego. Posługujemy się metodą różniczki zupełnej.

gdzie: d = dokładność odczytu odległości za pomocą suwmiarki

d=10-3 m

= dokładność odczytu kąta z podziałki umieszczonej na podstawie ramienia detektora.

=1=0,017 rad

Czyli:

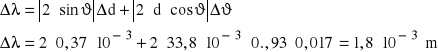
(n pomijamy bo n=1)

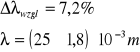
2. Obliczamy błąd wyznaczenia d(hkl) dla kryształu heksagonalnego.

gdzie: =1,8 10-3 m

=1=0,017 rad

Czyli:

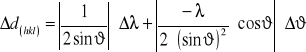
(n pomijamy jw.)

Po podstawieniu otrzymujemy:

- dla pierwszego ustawienia:

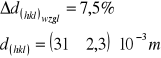
- dla drugiego ustawienia:

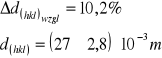
Laboratorium z Fizyki.

Strona nr 5

---