Zespół nr 1	Nogaj Kamil		WM
Ćwiczenie nr O4	Temat: Wyznaczenie współczynnika załamania za pomocą mikroskopu.		Mechanika i Budowa Maszyn
24.05.2000 r.
Teoria	Ocena:		Podpis:
Wykonanie

1. Opis teoretyczny:

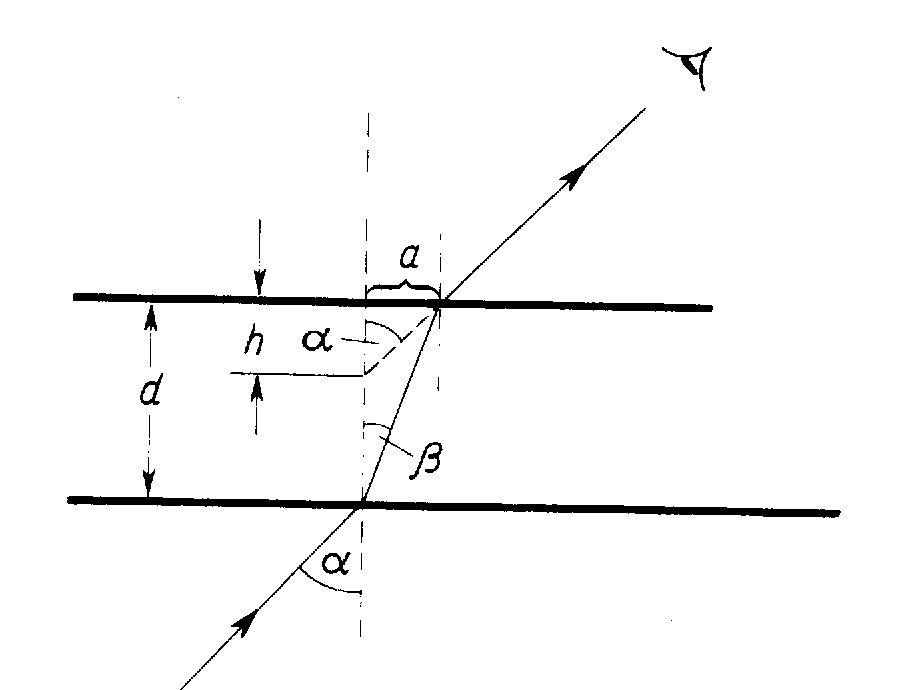
Na granicy dwóch środowisk światło ulega załamaniu. Załamaniem rządzą następujące prawa: kąt padania i kąt załamania leżą w jednej płaszczyźnie, a współczynnik załamania n jest stosunkiem sinusów kąta padania α i załamania β. Jeżeli kąt α jest bardzo mały, wtedy

zachodzi sin α = tg α= α i podobnie sin β = tg β = β.

Korzystając z tych założeń możemy napisać:

sin α = tg α=a /h

oraz sin β = tg β =a / h

stąd

Wielkość d mierzymy mikromierzem, wielkość h za pomocą mikroskopu. Na przedniej
i tylnej powierzchni badanej płytki znajdują się rysy. Nastawiamy mikroskop na ostrość widzenia rysy górnej i odczytując położenie tubusa a_g , a następnie odpowiednio rysy dolnej a_d. Pozorną grubość płytki obliczamy jako różnicę │a_d - a_g│. Stosowany mikroskop musi dawać możliwość pomiaru przesunięcia tubusa lub stolika. Większość mikroskopów ma wzorcowe obroty pokrętła precyzyjnego przesuwu tubusa, gdzie jeden obrót tego pokrętła odpowiada przesunięciu 0,1mm. Na pokrętle znajduje się skala pozwalająca odczytać położenie tubusa z dokładnością do 0,001 lub 0,01mm. Gdy brak jest takiej skali, zastosować możemy zwykły czujnik mikrometryczny opierając stopę jego żerdzi o ruchomą część mikroskopu.

2. Tabele pomiarowe.

I Próbka.

Lp	Górna płytka	Dolna płytka	Grubość rzeczywista	Grubość pozorna
1	9,68	7,10	4,15	2,58
2	9,86	7,15	4,15	2,71
3	9,9	7,30	4,15	2,6
4	9,8	7,15	4,15	2,65
5	9,85	7,10	4,15	2,75
6	9,76	7,09	4,15	2,67
7	9,8	7,16	4,15	2,64
8	9,69	7,2	4,15	2,49
9	9,79	7,06	4,15	2,73
10	9,85	7,11	4,15	2,74

Obliczam średnią rzeczywistą grubość pierwszej płytki:

Obliczam średnią pozorną grubość pierwszej płytki:

II Próbka.

Lp	Górna płytka	Dolna płytka	Grubość rzeczywista	Grubość pozorna
1	6,15	9,4	5,25	3,25
2	6	9,5	5,25	3,5
3	6,1	9,45	5,25	3,35
4	6	9,4	5,25	3,4
5	6,15	9,38	5,25	3,23
6	6,2	9,42	5,25	3,22
7	6,1	9,45	5,25	3,35
8	6	9,35	5,25	3,35
9	6,1	9,38	5,25	3,28
10	6,15	9,45	5,25	3,3

Obliczam średnią rzeczywistą grubość drugiej płytki:

Obliczam średnią pozorną grubość drugiej płytki:

III Próbka.

Lp	Górna płytka	Dolna płytka	Grubość rzeczywista	Grubość pozorna
1	6,97	9,98	4,15	3,01
2	6,95	9,64	4,16	2,69
3	6,98	9,7	4,15	2,72
4	6,96	9,66	4,15	2,7
5	6,97	9,68	4,16	2,71
6	7	9,7	4,15	2,7
7	6,95	9,64	4,15	2,69
8	6,97	9,7	4,15	2,73
9	6,97	9,69	4,15	2,72
10	6,98	9,7	4,16	2,72

Obliczam średnią rzeczywistą grubość trzeciej płytki:

Obliczam średnią pozorną grubość trzeciej płytki:

3. Obliczenia.

Współczynnik załamania:

Obliczam współczynnik załamania dla pierwszej płytki:

n_i= d_i / h_i n_i=1,5625

Obliczam współczynnik załamania dla drugiej płytki:

n_i= d_i / h_i n_i=1,5798

Obliczam współczynnik załamania dla trzeciej płytki:

n_i= d_i / h_i n_i=1,5162

3.2. Stosując metodę pochodnej logarytmicznej obliczam błąd w jakim wyznaczony został współczynnik załamania.

Błąd mikrometra Δd = 0,01 [mm].

Błąd mikroskopu Δh = 0,02 [mm].

n= d / h

ln n = ln d - ln h

• Dla pierwszej płytki:

Δn=0,016

n = 1,5625 ± 0,016

3.3 Obliczam błąd średni kwadratowy średnich arytmetycznych, przy pomiarze grubości pozornej i rzeczywistej płytek.

• Dla pierwszej płytki:

Dla grubości rzeczywistej

Dla grubości pozornej:

• Dla drugiej płytki:

Dla grubości rzeczywistej

Dla grubości pozornej

• Dla trzeciej płytki :

Dla grubości rzeczywistej

Dla grubości pozornej

4. Zestawienie wyników :

	I płytka	II płytka	III płytka
[mm]	4,15 ± 0,004	5,25 ± 0,0027	4,153 ±0,00153
[mm]	2,656 ± 0,028	3,323 ±0,0027	2,739 ± 0,03042

1

5

Politechnika Świętokrzyska w Kielcach

---