wyznaczanie równoważnika elektrochemicznego miedzi oraz st

*Sprawozdanie z wykonanego ćwiczenia nr 308*

*Temat:*	Wyznaczanie równoważnika elektrochemicznego miedzi oraz stałej Faraday'a.

*Imię i Nazwisko:*		Albin Kimsa Artur Redosz


*Wydział:*	*Semestr:*		*Rok akademicki:*
Elektryczny	trzeci		2000/2001

*Zespół:*	*Data wykonania:*	*Ocena:*	*Podpis:*
9	18.12.2000

Zagadnienia teoretyczne.

Drobiny związków chemicznych o wiązaniu jonowym w środowisku o dużej przenikalności elektrycznej łatwo ulegają rozpadowi na jony. Wynika to z osłabienia sił kulombowskiego oddziaływania jonów w drobinie. Sytuacja taka ma miejsce w przypadku soli, zasad lub kwasów w roztworze cieczy dipolowej. Cieczą to w praktyce najczęściej jest woda (ε=81). Proces rozpadu drobiny na jony pod wpływem rozpuszczalnika nazywamy dysocjacją elektrolityczną. Jonami dodatnimi (kationami) są jony reszty kwasowej lub grupy wodorotlenkowe OH. Równocześnie zachodzi proces odwrotny. Jony przeciwnych znaków spotkawszy się w toku termicznych ruchów mogą tworzyć obojętne drobiny. Ten proces określony jest mianem rekombinacji jonów. Intensywność obu tych procesów zależna jest od stężenia roztworu oraz temperatury. W każdych warunkach ustala się ściśle określony dla tych warunków stan równowagi dynamicznej między tymi dwoma procesami, któremu odpowiada określone stężenie par jonów w roztworze, lub ściślej: określony stopień dysocjacji. Stopień dysocjacji określony jest przez stosunek liczby jonów zdysocjowanych do ogólnej liczby jonów w jednostce objętości:

(1)

Wstawienie do takiego roztworu elektrolitycznego elektrod metalowych lub węglowych i wytworzenie między nimi różnicy potencjałów spowoduje powstanie pola elektrycznego, a pod jego wpływem (na jony działa siła
) uporządkowany ruch jonów (prąd jonowy): anionów ku anodzie (+) oraz kationów ku katodzie (-). Docierające do elektrod jony zobojętniają się oddając elektrodzie ładunek, same zaś bądź wydzielają się w czystej chemicznie postaci, bądź wchodzą w reakcje z atomami elektrod lub innymi atomami otoczenia.

Tak więc przepływowi prądu przez elektrolit towarzyszą reakcje chemiczne. Zjawisko to określa się mianem elektrolizy. Ku elektrodom nie poruszają się same jony powstałe w wyniku dysocjacji. Jony te w wyniku elektrostatycznego oddziaływania z dipolowymi drobinami rozpuszczalnika otaczają się nimi. Proces ten w ogólnym przypadku nazywamy solwatacją, a w przypadku wodnych roztworów hydratacją jonów. Wynikiem solwatacji jonów jest ich zmniejszona ruchliwość, co wydajnie zmniejsza przewodnictwo właściwe elektryczne elektrolitów określone równaniem:

(2)

gdzie: e-ładunek elementarny, z-wartościowość jonów, n-liczba drobin substancji elektrolitycznej w jednostce objętości, α-stopień dysocjacji, u_A,u_K-ruchliwości odpowiednio anionów i kationów, przy czym, w ogólnym przypadku:

Należy tu wspomnieć, że ruchliwość kationów będzie również osłabiana przeciwnym ruchem anionów. Wraz ze wzrostem temperatury rośnie stopień dysocjacji oraz ruchliwość jonów, a więc przewodnictwo elektrolitów również rośnie (odwrotnie niż w metalach).

Wspomniane już wydzielanie się substancji chemicznych na elektrodach podlega prawom Faraday'a. Pierwsze z nich mówi, że masa substancji wydzielonej na każdej z elektrod jest proporcjonalna do wartości ładunku przeniesionego przez elektrolit:

(3)

gdzie: k-równoważnik elektrochemiczny równy liczbowo masie substancji wydzielonej przez prąd o natężeniu 1A w ciągu 1s, I-natężenie prądu płynącego przez elektrolit, t-czas przepływu prądu, Q=I·t ładunek niesiony przez elektrolit.

Drugie prawo Faraday'a stwierdza, że masy substancji wydzielonych na dowolnej elektrodzie z dowolnego roztworu takim samym prądem i w ciągu takiego samego czasu mają się do siebie tak, jak równoważniki chemiczne tych substancji:

(4)

gdzie: R=A/z równoważnik chemiczny substancji, A-masa atomowa substancji, z-wartościowość.

Uwzględniając (3) i (4) można napisać:

(5)

lub

(6)

gdzie: F-stała Faraday'a.

Stosując stałą Faraday'a, równanie (3) można zapisać:

(7)

Z równania (6) wynika, że stała Faraday'a ma wymiar ładunku elektrycznego, zaś z równania (7) wynika, że gdy F=I·t, wydzielona zostanie masa m=R, czyli masa jednego równoważnika chemicznego. Stała Faraday'a równa jest ładunkowi związanego z wydzieleniem na dowolnej elektrodzie jednego gramo- lub kilogramorównoważnika chemicznego. Stosując konsekwentnie układ SI należy używać pojęcia kilogramorównoważnika. W tym przypadku wartość stałej Faraday'a wynosi:

[A·s·(kilogramorównoważnik)^-1]

F=N·e (8)

Gdzie: N-liczba Avogadro dla kilomola, e-ładunek elementarny

Przewodnictwo elektrolitów - ogólnie

Jeżeli cząsteczki o budowie jonowej (wiązaniu jonowym) umieścić w ośrodku o względnej przenikalności elektrycznej ε_r>1, to ośrodek osłabia siły wiązania jonowego, a wielkość sił osłabiających wyraża prawo Coulomba:

(9)

gdzie: q₁, q₂-ładunki jonów, r-odległość między ładunkami e, ε_r-względna przenikalność elektryczna ośrodka.

W roztworach wodnych siły wiązania jonowego są np. osłab 0x08 graphic
iane 81 razy. Cząsteczki wody tworzą silnie rozciągnięte dipole, a oddziałując z drobinami soli, zasad czy kwasów dążą do rozerwania ich na jony. Proces rozrywania pokazuje rysunek obok.

Po przyłożeniu zewnętrznego pola elektrycznego zaczyna płynąć prąd - proces ten opisano wyżej. W celu określenia gęstości prądu jonowego obliczamy, jaki ładunek jest przenoszony w ciągu jednostki czasu przez jednostkę pola powierzchni przekroju prostopadłego do kierunku ruchu jonów. Jony dodatnie poruszające się ze średnią prędkością
tworzą prąd o gęstości j₊

(10)

gdzie: q₊ -ładunek jonu dodatniego, n₀₊ - stężenie jonów dodatnich w roztworze,
-średnia prędkość uporządkowanego ruchu jonów dodatnich.

Jeżeli założymy, że podczas ruchu jonów siła tarcia jest proporcjonalna do jego prędkości
(gdzie η₊ jest współczynnikiem tarcia jonu dodatniego) i że jest ona równa sile, z jaką działa na jon pole elektryczne, to otrzymamy T=F, czyli
, skąd otrzymujemy:

(11)

Występujący w równaniu ułamek oznaczamy u₊ i nazywamy ruchliwością jonu. Jest ona równa liczbowo średniej prędkości jonu pod wpływem pola elektrycznego o jednostkowym natężeniu (patrz wyżej):
. Uwzględniając dotychczas otrzymane zależności gęstość prądu jonów dodatnich możemy więc zapisać: j₊=q₊·u₊·n₀₊·E, zaś gęstość prądu jonów ujemnych: j_-=q_-·u_-·n_0-·E, gdzie q_- oznacza wartość bezwzględną ładunku jonu ujemnego. Wypadkowa gęstość prądu będzie sumą wyprowadzonych gęstości, czyli (uwzględniając, że elektrolit jako całość jest elektrycznie obojętny) po przekształceniach otrzymujemy: j=q₊·n₀₊·(u₊+u_-)·E

Ładunek q₊ jonu równa się liczbowo ładunkowi e pomnożonemu przez wartościowość jonu z₊:

, co z kolei daje:

(12)

Jest to prawo Ohma w ujęciu elektronowym. Porównując je z prawem Ohma dla gęstości prądu
otrzymamy wzór na rezystywność elektrolitu ρ (oporność właściwą).

Elektrolitem w niniejszym ćwiczeniu jest wodny roztwór siarczanu miedzi CuSO₄, elektrodami zaś dwie płytki miedziane. Naczynie elektrolityczne wraz z roztworem i elektrodami nazywane jest krótko woltametrem. W stosowanym woltametrze, po zamknięciu obwodu pokazanego na rysunku nastąpi wydzielanie się na katodzie miedzi z roztworu. Przy anodzie jony reszty kwasowej SO₄ 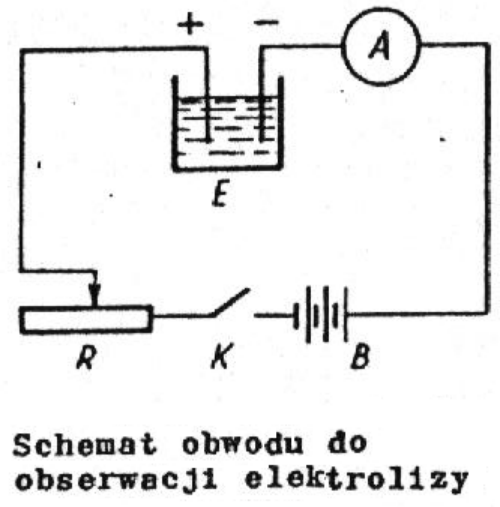0x08 graphic
zobojętniają się i reagują z miedzią elektrody tworząc drobinę CuSO₄. Tak więc masa katody rośnie, a anody maleje. Określając natężenie prądu, czas jego przepływu oraz masę miedzi wydzielonej na katodzie można z równania (3) wyznaczyć równoważnik elektrochemiczny oraz z równania (6) stałą Faraday'a i z równania (8) ładunek elementarny.

Przeprowadzenie ćwiczenia

wyznaczono masę m₁ jednej z elektrod,
włożono elektrody do woltametru, złożono obwód elektryczny tak, aby zważona elektroda była katodą,
zmierzono odległość d między elektrodami
włączono zasilacz prądowy, ustawiono na 1A i zmierzono napięcie U₁ między elektrodami,
po ściśle określonym czasie (tu: 20 minut) zmierzono napięcie U₂ i wyłączono zasilanie oraz wyjęto katodę,
zważono ponownie katodę oraz zmierzono wymiary a i b określające na elektrodzie powierzchnię, która była zanurzona,
wyznaczono masę miedzi m=m₂-m₁,
pomiary powtórzono jeszcze kilkakrotnie.

Tabele pomiarowe

Lp.	I	t	m₁	m₂	m	k	F	Δk	ΔF
-	A	s	kg	kg	kg		C		C
1	1	1200	0,2393	0,2360	-0,0033	-2,750·10^-6	-23116·10³	0,03896·10^-6	331,12·10³
2	1	1200	0,2368	0,2381	0,0013	1,083·10^-6	58680·10³	0,01535·10^-6	840,54·10³
3	1,5	600	0,2381	0,2379	-0,0002	-0,222·10^-6	-286065·10³	0,00333·10^-6	4336,26·10³

Lp.	I	U₁	U₂		d		a	b	S	j	γ
-	A	V	V	V	m		m	m	m²
1	1	2,92	2,84	2,88	0,0550	52,36	0,1046	0,0662	0,0069245	144,41	2,75791
2	1	0,97	0,984	0,977	0,0202	48,37	0,1045	0,0658	0,0068671	145,43	3,00687
3	1,5	5,95	5,85	5,9	0,0832	70,91	0,0961	0,0664	0,0063810	235,07	3,31491