Wahadło torsyjne, ciało o momencie bezwładności I, zawieszone na sprężystej nici (pręcie) o określonym momencie skręcającym. Okres drgań wahadła torsyjnego wynosi

T = 2π(I/D)1/2

, gdzie D - moment skręcający powodujący skręcenie o jednostkowy kąt.

Prawo Webera-Fechnera

Prawo Webera-Fechnera - zasada mówiąca o relacji pomiędzy fizyczną miarą bodźca a reakcją układu biologicznego. Dotyczy ono reakcji na bodźce takich zmysłów jak wzrok, słuch czy poczucie ciepła. Jest to zasada fenomenologiczna będąca wynikiem wielu obserwacji praktycznych i znajdująca wiele zastosowań technicznych.

Wartość reakcji układu biologicznego jest proporcjonalna do logarytmu bodźca.

w=k*ln(B/B0)

gdzie:

w - reakcja układu biologicznego (wrażenie zmysłowe)

B - natężenie danego bodźca

B0 - wartość początkowa natężenia danego bodźca

ln - logarytm naturalny

Tak więc ocena głośności dźwięku zależy od logarytmu ciśnienia akustycznego na membranie bębenka, zaś ocena jasności światła zależy od logarytmu strumienia światła mierzonego na powierzchni oka. Właśnie z powodu stosowalności zasady W-F w pomiarze głośności dźwięków stosuje się jednostki ilorazowe jak bel i jego podwielokrotności.

Inną konsekwencją zasady W-F jest fakt, że aby uzyskać liniową skalę np. w pokrętle głośności radia (dwa razy dalsza pozycja daje dwa razy głośniejszy dźwięk) należy stosować potencjometr logarytmiczny.

Przejawem tego prawa jest także znana od czasów starożytnych wielkość gwiazdowa. Bodźcem jest światło wpadające do oka, reakcją jasność gwiazdy w wielkościach gwiazdowych. Magnitudo gwiazdy zmienia się o 5 jednostek, gdy natężenie jej światła zmienia się stokrotnie. (Kazimierz Gębarski, Tomasz Kwast "500 zagadek astronomicznych" Warszawa 1984 WP s. 207) Por. absolutna wielkość gwiazdowa.

Efekt Joule'a Thomsona

(Przekierowano z Zjawisko Joule'a Thomsona)

W procesie Joule'a Thomsona gaz jest przeciskany z obszaru o ciśnieniu p1 do obszaru o ciśnieniu p2, przy czym: p1 > p2

Zmiana temperatury gazu rzeczywistego podczas izoentalpowego przeciskania gazu przez porowatą przegrodę(dławienie) z obszaru o wyższym ciśnieniu do obszaru o ciśnieniu niższym. Zmiana temperatury jest zależna od tzw. współczynnika Joule'a-Thomsona:

gdzie:

n - liczba moli gazu

Cp - ciepło molowe gazu

H - entalpia

Gdy μ jest ujemny temperatura gazu w procesie Joule'a-Thomsona rośnie, zaś dla dodatniego μ temperatura maleje. W przypadku gazu doskonałego współczynnik Joule'a-Thomsona jest tożsamościowo równy zeru. Zależności te prezentuje poniższa tabela:Znak współczynnika Zakres temperatur Zmiana temperatury Uwagi

μ > 0 niskie ΔT < 0 tzw. dodatni efekt

μ < 0 wysokie ΔT > 0 tzw. ujemny efekt

Efekt Joule'a-Thomsona stosuje się m.in przy skraplaniu gazów.

Zasady terodynamiki

Trzecia zasada termodynamiki (zasada Nernsta) może być sformułowana jako postulat: nie można za pomocą skończonej liczby kroków uzyskać temperatury zera bezwzględnego (zero kelwinów), jeżeli za punkt wyjścia obierzemy niezerową temperaturę bezwzględną.

Inne sformułowanie głosi, że entropia substancji tworzących doskonałe kryształy dąży do 0 gdy temperatura dąży do 0 K.

Mówiąc jaśniej, gdyby udało się schłodzić jakąś substancję do 0 K i gdyby ona utworzyła kryształ doskonały to jej entropia musiałaby przyjąć wartość 0. Jest to jednak technicznie, a także formalnie niewykonalne, dlatego definicja trzeciej zasady termodynamiki w formie:

entropia kryształu doskonałego w temperaturze zera bezwzględnego jest równa 0

nie jest poprawna, choć intuicyjnie akceptowalna.

Druga zasada termodynamiki stwierdza, że w układzie zamkniętym istnieje addytywna funkcja stanu, zwana entropią S, która jest rosnącą funkcją energii wewnętrznej oraz której zmiana ΔS w procesie adiabatycznym spełnia nierówność
, przy czym równość zachodzi wtedy i tylko wtedy, gdy proces jest odwracalny.

W uproszczeniu można to wyrazić też tak:

"W układzie zamkniętym w dowolnym procesie entropia nigdy nie maleje"

Pierwsza zasada termodynamiki to prosta zasada zachowania energii, czyli ogólna reguła głosząca, że energia w żadnym procesie nie może pojawić się "znikąd".

Zmiana energii wewnętrznej układu ΔU = ΔQ + ΔW

Istnieją różne sformułowania tej zasady, zależnie od sytuacji:

Sformułowanie najbardziej ogólne:

Energia wewnętrzna układu izolowanego nie zmienia się, niezależnie od przemian zachodzących w tym układzie.

Sformułowanie dla procesów cieplno-mechanicznych:

Zmiana energii wewnętrznej układu jest równa sumie pracy wykonanej przez układ bądź nad układem i ciepła dostarczonego lub oddanego przez układ.

Doświadczalną podstawą pierwszej zasady jest doświadczenie Joule'a i pokrewne mu, które dowodzą równoważności ciepła i pracy mechanicznej przez pokazanie możliwości całkowitej zamiany pracy na ciepło. Uznanie ciepła jako innego niż praca sposobu zmiany energii prowadzi w naturalny sposób do włączenie ciepła do zasady zachowania energii. Pierwsza zasada termodynamiki jest dokładnie tym prawem.

Joule, Mayer (1842), Helmholtz (1847): Zmiana energii wewnętrznej układu równa jest dostarczonemu do układu ciepłu i pracy wykonanej nad układem przez siły zewnętrzne:

ΔU = ΔW + ΔQ

Gdzie:

ΔU - zmiana energii wewnętrznej układu

ΔQ - ciepło wymienione przez układ z otoczeniem, jeśli układ oddaje ciepło, jego energia wewnętrzna maleje

ΔW - praca wykonana przez układ lub nad układem

Pierwsza zasada termodynamiki pozwala na zdefiniowanie energii wewnętrznej jako funkcji stanu: dla wszystkich procesów prowadzących od pewnego określonego stanu do drugiego, zmiana ΔU ma zawsze tę samą wartość, choć ilości dostarczanego ciepła i wykonanej pracy są na ogół różne dla różnych procesów.

Ciepło właściwe molowe [edytuj]

Ciepło właściwe molowe definiuje wzór:

gdzie:

C - molowe ciepło właściwe, (J/mol K)

n - liczność (ilość substancji w molach)

Q - ciepło dostarczane do układu

By odróżnić ciepło właściwe molowe oznacza się je wielką literą C.

Posługiwanie się ciepłem właściwym molowym jest wygodne, bo dla wielu substancji ma ono taką samą lub podobną wartość.

W przypadku gazów ciepło właściwe zależy od rodzaju przemiany, dlatego wprowadzono pojęcie ciepła właściwego przy stałym ciśnieniu cp (ciepło właściwe przemiany izobarycznej) i przy stałej objętości cv (ciepło właściwe przemiany izochorycznej). Cp i Cv używa się w obliczeniach zależnie od tego, czy dana przemiana zachodzi przy stałym ciśnieniu czy przy stałej objętości gazu.

Dla gazu doskonałego zachodzi zależność między molowymi ciepłami właściwymi:

gdzie: MR - uniwersalna stała gazowa (MR = 8.314 J/(mol K)).

Klasyczna teoria ciepła właściwego określa, że energia kinetyczna na jeden stopień swobody (oznaczany zwykle literą i) (zasada ekwipartycji energii) jednej cząsteczki wynosi kT/2, zatem energia jednego mola gazu doskonałego, która jest sumą energii kinetycznej cząsteczek wyraża się wzorem:

gdzie:

i - liczba stopni swobody cząsteczki,

N - liczba cząsteczek liczba Avogadra

k - stała Boltzmana,

T - temperatura

Dla:

jednoatomowego gazu i = 3, dlatego Cv = 3 / 2Nk = 12,5J / (molK)

dwuatomowego gazu i = 5, dlatego Cv = 5 / 2Nk = 20,8J / (molK)

Wartości te odpowiadają wyznaczonym ciepłom właściwym gazów szlachetnych (12,5 J/(molK), azotu (20,8 J/(molK), tlenu (20,9 J/(molK) i wodoru (20,3 (J/molK). W niskich temperaturach i pod dużym ciśnieniem ciepło właściwe zmniejsza się.

W przypadku ciał stałych ciepło właściwe w niskich temperaturach zależy od trzeciej potęgi temperatury. Ta zależność może być wyprowadzona z modelu Debye'a. Pierwszym historycznie modelem był model Einsteina.

Pompa dyfuzyjna[edytuj]

Pompa dyfuzyjna - rodzaj pompy próżniowej, w której strumień czynnika pompującego (specjalnego oleju lub rtęci) wskutek m.in. zjawiska dyfuzji porywa ze sobą cząsteczki gazu przenosząc je z obszaru próżni wysokiej (z obszaru pompowanego) do obszaru próżni wstępnej.

Zasada działania [edytuj]

Strumień par czynnika pompującego uzyskuje się wskutek ogrzania do wrzenia oleju mineralnego lub rtęci. Służy do tego najczęściej grzejnik elektryczny, umieszczony na dnie pompy. Pary wrzącego czynnika za pomocą systemu dysz unoszą się do góry pompy i wylatują z nich pod kątem ostrym, porywając gaz w dół pompy. U dołu znajduje się wylot do pompy próżni wstępnej. Pary czynnika skraplają się na ściankach pompy, które są chłodzone wodą lub powietrzem. Czynnik ścieka na dół pompy, gdzie znów podlega wrzeniu.

Konstrukcja [edytuj]

Ilość dysz może być różna (najczęściej od jednej do trzech) - pompa jest wtedy jedno-, dwu-, lub trójstopniowa. Ostatni stopień, najbliżej wylotu do próżni wstępnej często wykonuje się jako eżektorowy. Dzięki temu pompa może pracować przy gorszej próżni wstępnej. Potrzebna próżnia wstępna wynosi zazwyczaj 0,01 - 0,5 Tr dla pomp olejowych i do 20 Tr dla pomp rtęciowych. Przy wyższym ciśnieniu próżni wstępnej pompa dyfuzyjna przestaje pracować.

Ze względu na konstrukcję pompy dyfuzyjne mogą być szklane i metalowe.

Zastosowanie [edytuj]

Za pomocą typowych pomp dyfuzyjnych można uzyskiwać ciśnienia 10-5 - 10-7 Tr, a nawet niższe. Pogorszenie próżni wstępnej jest szkodliwe dla działania pompy dyfuzyjnej (zwłaszcza olejowej), gdyż olej ulega utlenieniu, co pogarsza parametry pompy.

Pewną wadą pomp dyfuzyjnych jest występowanie wstecznego strumienia par czynnika, który podąża do obszaru pompowanego, psując próżnię. Za pomocą odrzutników i wymrażaczy można temu zjawisku w znacznym stopniu zapobiec.

Pompy dyfuzyjne w wielu zastosowaniach ustąpiły miejsca pompom turbomolekularnym oraz jonowym.

Ruchy Browna[edytuj]

Ruchy Browna to chaotyczne ruchy cząsteczek płynu i gazu , powodujące jego lokalne, chwilowe zmiany gęstości. Ruchy Browna są najczęściej spowodowane nierównomiernym rozkładem temperatury w płynie, dowiedziono jednak, że występują one nawet w płynach, w których rozkład temperatury jest całkowicie równomierny, a ich przyczyną jest kwantowa struktura materii.

W 1827 roku brytyjski biolog Robert Brown obserwując przez mikroskop pyłki kwiatowe w zawiesinie wodnej dostrzegł, iż znajdują się one w nieustannym, chaotycznym ruchu, a nie - jak sądził - stoją w miejscu.

Opis ruchów Browna [edytuj]

Autorami matematycznego opisu ruchów Browna byli niezależnie Albert Einstein (w 1905 roku) i Marian Smoluchowski (w 1906). Obaj naukowcy zauważyli, że przypadkowe błądzenie pyłków jest wywołane bombardowaniem ich przez cząsteczki wody. Cząsteczki wody są dużo mniejsze, jest ich wiele oraz poruszają się bardzo szybko. Różnice w prędkości ruchu oraz ilości uderzających cząsteczek z poszczególnych stron są przyczyną ruchów drobin pyłku w cieczy.

Przykłady ruchów Browna [edytuj]

cząsteczki tłuszczu na mleku

pyłek kwiatowy na wodzie

mgła

rozpylone w powietrzu perfumy

krople tuszu na wodzie

Galwanometr

Konstrukcja galwanometru

Galwanometr to bardzo czuły miernik magnetoelektryczny. Służy on do mierzenia niewielkich wartości natężenia prądu elektrycznego (wykrywa nawet tysięczne części ampera), może też służyć do sygnalizacji stanu równowagi mostka elektrycznego.

Rozróżnia się kilka rodzajów galwanometrów, między innymi ze względu na budowę wewnętrzną - ze stałym uzwojeniem i ruchomym magnesem, ze stałym magnesem i ruchomym uzwojeniem, oraz ze względu na sposób wskazywania - galwanometr ze wskazówką, galwanometr zwierciadlany, galwanometr z wbudowanym źródłem światła.

Galwanometr stosowany był powszechnie w precycyjnych przyrządach pomiarowych w XX w., później wyparty został przez cyfrowe metody pomiaru. Na zdjęciu ustrój pomiarowy klasycznego galwanometru ze stałym magnesem i ruchomą cewką, ze wskazówką.

Budowa i działanie galwanometru

Weźmy cienką prostokątną ramkę, zawieszoną na nitce pomiędzy magnesami (N i S). Dodatkowo w ramkę jest wsunięty rdzeń, dzięki któremu uzyskuje się niemal radialny rozkład natężenia pola magnetycznego. Na ramkę działają siły pochodzące od pola magnetyczego (moment obrotowy ramki), oraz siła pochodząca od nici podtrzymującej ramkę (moment skręcający pochodzący od stabilności nici). Oba momenty częściowo się równoważą, dlatego też, gdy przez ramkę przepłynie prąd, to ramka wychyli się ze swego położenia równowagi do nowego położenia równowagi. Kąt wychylenia ramki jest proporcjonalny do prądu płynącego przez ramkę. Jeśli do ramki przypniemy wskazówkę lub lekkie zwierciadło, będziemy mogli obserwować wychylenie ramki, a więc i natężenie prądu płynącego przez ramkę galwanometru.

Ponieważ galwanometr jest urządzeniem bardzo czułym, nie możemy go podpiąć do układu bezpośrednio, wymagane jest zabezpieczenie.

Rozkład Boltzmanna

Rozkład Boltzmanna - bardzo ogólne, powszechnie stosowane w fizyce i chemii, równanie określające sposób obsadzania poziomów energetycznych przez atomy, cząsteczki lub inne indywidua cząsteczkowe (cząstki) w stanie równowagi termicznej.

Równanie Boltzmanna pozwala okreslić tzw. funkcję rozkładu energii dla układów zawierających tak duże liczby obiektów, że stosują się do tzw. prawa wielkich liczb i można stosować do nich metody termodynamiki statystycznej, np. do gazu doskonałego lub gazu rzeczywistego. Przy stosowaniu rozkładu Boltzmanna nie jest wymagana szczegółowa wiedza na temat charakteru poziomów energetycznych.

W najprostszej postaci przedstawia stosunek obsadzeń Ni/Nj przez obiekty mikroskopowe dla dwu stanów "i", "j" różniących się energią:

gdzie:

Ni, Nj - liczba obiektów w stanach "i", "j"

ΔEij = Ei − Ej - różnica energii dla stanów "i", "j"

k - stała Boltzmanna, k = R/NA (R - (uniwersalna) stała gazowa, NA - stała Avogadra)

T - temperatura

Jak widać oprócz różnicy energii zasadniczą rolę odgrywa temperatura. Zgodnie z rozkładem Boltzmanna dla temperatury dążącej do zera będą obsadzone jedynie najniższe, podstawowe poziomy energetyczne.

Jeżeli dane poziomy są zdegenerowane (dla danej energii istnieje gi poziomów o tej samej energii obsadzenia) wówczas prawdopodobieństwa obsadzenia rosną proporcjonalnie do degeneracji:

gdzie:

gi, gj - degeneracja poziomów "i", "j" (liczba stanów zdegenerowanych odpowiadających tej samej energii)

Uwzględniając możliwość obsadzenia wszystkich stanów otrzymamy:

gdzie:

N - liczba wszystkich obiektów (cząsteczek)

-
tzw. suma stanów (funkcja rozdziału)

W przypadku obecności stanów zdegenerowanych:

gdzie:

-
suma stanów uwzględniająca degenerację

Rozkład Boltzmanna jest zasadniczo rozkładem, w którym prawdopodobieństwo obsadzenia stanu maleje wykładniczo wraz z energią poziomu, jednak w przypadku silnej degeneracji niektórych poziomów, mogą być one silniej obsadzone niż niższe poziomy.

W przypadku bardzo wysokiej temperatury (T → ∞) wszystkie czynniki typu exp(-E/kT) stają się równe jedności (oczywiście gdy E << kT) i wówczas wszystkie stany są jednakowo prawdopodobne, a rozkład Boltzmanna przechodzi wówczas w rozkład jednostajny.

Pojemność cieplna[edytuj]Spis treści [ukryj]

1 Definicja

2 Pojemność cieplna gazów

Definicja [edytuj]

Pojemność cieplna - stosunek ilości ciepła (dQ) dostarczonego do układu, do odpowiadającego mu przyrostu temperatury (dT).

gdzie:

C - pojemność cieplna

Q - ciepło

T - temperatura

Pojemność cieplna przypadająca na jednostkę masy to ciepło właściwe a na 1 mol to molowe ciepło właściwe (ciepło molowe).

Pojemność cieplna C jest związana z ciepłem właściwym poprzez prostą zależność:

gdzie:

c - ciepło właściwe

m - masa substancji

Pojemność cieplną oblicza się często na podstawie molowego ciepła właściwgo (ciepła molowe) wg wzoru:

gdzie:

M - masa molowa

Wygodnie jest rozpatrywać pojemność cieplną molową. W wszystkich równaniach poniżej używa się właśnie molowych pojemności cieplnych.

Pojemność cieplna gazów [edytuj]

W przypadku układów zawierających fazy nieskondensowane (gazy i pary) często konieczne jest jeszcze rozróżnienie warunków w których mierzona jest (molowa) pojemność cieplna:

dla przemiany izochorycznej (przy stałej objętości układu, V=const):

dla przemiany izobarycznej (przy stałym ciśnieniu w układzie, p=const):

Dla jednoatomowego gazu doskonałego, gdzie energia wewnętrzna składa się jedynie z energii kinetycznej ruchu postępowego cząsteczek - na każdy stopień swobody przypada kT/2 (RT/2 dla mola cząsteczek):

Dla cząsteczek wieloatomowych, w zależności od ich budowy pojemność cieplna rośnie, gdyż oprócz ruchu postępowego cząsteczek mamy do czynienia z obrotem - dla cząsteczek liniowych możliwy jest wzrost energii cząsteczek poprzez obrót w 2 prostopadłych kierunkach, skąd:

Dla cząsteczki o budowie nieliniowej (obrót w 3 prostopadłych kierunkach):

Cv,nielin = 3R

Dla wszystkich gazów doskonałych dla przemiany izobarycznej:

Cp = Cv + R

Skąd dla gazu jednoatomowego:

Prawo Daltona[edytuj]

Prawo Daltona to wspólne określenie na dwa różnie prawa, prawo ciśnień cząstkowych, prawo objętości cząstkowych, oba zaproponowane przez Johna Daltona, które są wzajemnie komplementarne.Spis treści [ukryj]

1 Prawo ciśnień cząstkowych

2 Prawo objętości cząstkowych

3 Wyprowadzenie

3.1 Ciśnienie cząstkowe

3.2 Objętość cząstkowa

Prawo ciśnień cząstkowych [edytuj]

Prawo ciśnień cząstkowych zostało opublikowane przez Daltona w 1810 r. Głosi ono:

"Ciśnienie wywierane przez mieszaninę gazów jest równe sumie ciśnień wywieranych przez składniki mieszaniny, gdyby każdy z nich był umieszczany osobno w tych samych warunkach objętości i temperatury (suma ciśnień cząstkowych)."

W formie matematycznej można je wyrazić jako:

gdzie:

P - ciśnienie w mieszaninie k-składnikowej (objętość V i temperatura T)

pi - ciśnienie cząstkowe (parcjalne) składnika "i" (objętość V i temperatura T)

Prawo Daltona jest słuszne dla gazów doskonałych nie reagujących z sobą. Dla gazów rzeczywistych jest słuszne jedynie dla gazów rozrzedzonych i w temperaturze znacznie powyżej punktu krytycznego.

Efekt Magnusa

Linie prądu płynu wokół obracającego i poruszającego się ciała

Efektem Magnusa nazywamy zjawisko z zakresu dynamiki płynów polegające na powstawaniu siły prostopadłej do kierunku ruchu działającej na obracający się walec lub inną obrotową bryłę poruszającą się względem płynu (cieczy, gazu).

Efekt odkryty przez niemieckiego fizyka Heinricha Gustava Magnusa w 1853 roku.

Zjawisko wpływa znacznie na przykład na tor lotu wirującej piłki, może być stosowane do wyznaczania prędkości przepływu płynu.

Wartość siły określa prawo Kutty-Żukowskiego, mówiące, że jeżeli nieściśliwy płyn opływa nieskończenie długi walec, którego oś jest ustawiona prostopadle do kierunku przepływu niezaburzonego, to na jednostkę długości walca działa siła nośna określona wzorem:

W pobliżu powierzchni obracającego się walca na skutek adhezji prędkość obwodowa cząsteczek płynu jest taka sama jak prędkość obwodowa walca i wynosi dla walca o promieniu 'a'

cyrkulacja prędkości będzie równa:

a siła

gdzie:

ρ - gęstość płynu,

V - prędkość płynu,

a - promień walca

Γ - oznacza cyrkulację prędkości wzdłuż dowolnego konturu zamkniętego obejmującego jeden raz walec.

Teoretyczne i uzyskiwane drogą pomiaru wartości współczynnika siły nośnej

Można też wyrazić siłę nośną za pomocą wzoru:

Z porównania wzorów wynika, że:

Wartości współczynnika siły nośnej uzyskane drogą pomiaru okazują się być mniejsze od przewidzianych powyższym wzorem. Ruch cyrkulacyjny w płynach rzeczywistych, powodowany obrotem walca, nie jest bowiem identyczny z cyrkulacyjnym opływem walca płynem doskonałym, między innymi ze względu na występowanie tak zwanej warstwy przyściennej.

Soliton[edytuj]

(Przekierowano z Solitony)

W matematyce i fizyce soliton to samopodtrzymująca się odosobniona fala wywołana przez efekty nieliniowe występujące w materiale prowadzącym falę. Solitony towarzyszą wielu zjawiskom fizycznym, pojawiają się też jako rozwiązania nieliniowych cząstkowych równań różniczkowych.

Zjawisko solitonu zostało po raz pierwszy opisane przez Johna Scotta Russella, który zaobserwował falę solitonu w kanale wodnym (Union Canal, Wielka Brytania), a następnie odtworzył to zjawisko w specjalnie przygotowanym zbiorniku wodnym. Zaobserwowaną falę Russell nazwał "falą przesunięcia" (ang. wave of translation).

Trudno precyzyjnie zdefiniować czym jest soliton. Drazin and Johnson (1989) zdefiniowali soliton jako rozwiązanie układu nieliniowych równań różniczkowych, które

reprezentują fale o niezmiennym kształcie,

są zlokalizowane tak, że zanikają lub osiągają stałą wartość w nieskończoności,

mogą oddziaływać silnie z innymi solitonami, ale po kolizji zachowują niezmienioną formę - występuje tylko przesunięcie fazy

Są znane tylko jednowymiarowe solitony. Nie wiadomo, czy dwu- i trójwymiarowe w ogóle istnieją.

Zasada Huygensa

Przejście fali między ośrodkami a Zasada Huygensa

Zasada Huygensa (czytaj: hojchensa) sformułowana przez Christiaana Huygensa mówiąca, iż każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Fale te zwane są falami cząstkowymi i interferują ze sobą. Wypadkową powierzchnię falową tworzy powierzchnia styczna do wszystkich powierzchni fal cząstkowych i ją właśnie obserwujemy w ośrodku.

Z zasady Huygensa wynika, iż fale rozchodzą się izotropowo, a więc również wstecznie. W rzeczywistości nie jest to osiągalne, co zostało udowodnione empirycznie. Poprawkę zasady wprowadził Kirchhoff dodając współczynnik kierunkowy, równy:

Fraktal[edytuj]

(Przekierowano z Fraktale)

Fraktal (łac. fractus - złamany, cząstkowy) w znaczeniu potocznym oznacza zwykle obiekt samo-podobny (tzn. taki, którego części są podobne do całości) albo "nieskończenie subtelny" (ukazujący subtelne detale nawet w wielokrotnym powiększeniu). Ze względu na olbrzymią różnorodność przykładów matematycy obecnie unikają podawania ścisłej definicji i proponują określać fraktal jako zbiór, który:

ma nietrywialną strukturę w każdej skali,

struktura ta nie daje się łatwo opisać w języku tradycyjnej geometrii euklidesowej,

jest samo-podobny, jeśli nie w sensie dokładnym, to przybliżonym lub stochastycznym,

jego wymiar Hausdorffa jest większy niż jego wymiar topologiczny,

ma względnie prostą definicję rekurencyjną,

ma naturalny ("poszarpany", "kłębiasty" itp.) wygląd.

Dokładniej, fraktalem nazwiemy zbiór który posiada wszystkie te charakterystyki albo przynajmniej ich większość (zob. Falconer (1997)). Na przykład linia prosta na płaszczyźnie jest formalnie samo-podobna, ale brak jej pozostałych cech i zwyczajowo nie uważa się jej za fraktal. Z drugiej strony, zbiór Mandelbrota ma wymiar Hausdorffa równy 2, taki sam jak jego wymiar topologiczny. Jednak pozostałe cechy wskazują, że jest to fraktal.

Fraktale znane są powszechnie ze swej urody, której przykłady podziwiać można na ilustracjach poniżej.

Krzywe Lissajous

(Przekierowano z Krzywa Lissajous)

Krzywe Lissajous (figury Lissajous) to w matematyce krzywe opisane przez równania parametryczne

opisujące drgania harmoniczne. Tą rodzinę krzywych zbadał Nathaniel Bowditch w 1815, badania kontynuował Jules Antoine Lissajous.

Kształt krzywych jest szczególnie uzależniony od współczynnika a/b. Dla współczynnika równego 1, krzywa jest elipsą, ze specjalnymi przypadkami okrąg (A = B, δ = π/2 radianów) oraz odcinek (δ = 0). Inne wartości współczynnika dają bardziej złożone krzywe, które są zamknięte tylko gdy a/b jest liczbą wymierną.

Jedną z metod uzyskiwania krzywych Lissajous jest podanie na wejścia oscyloskopu, pracującego w trybie XY, dwóch sygnałów sinusoidalnych o częstotliwościach pozostających w stosunku a/b. Ciekawy efekt uzyskuje się również, gdy stosunek tych częstotliwości jest minimalnie różny: dzięki płynnej zmianie fazy (parametru δ) uzyskuje się dobrą iluzję trójwymiarowości - krzywa wydaje się "obracać". W najprostszm przypadku a ≈ b otrzymujemy efekt "kręcącej się monety".

Krzywe Lissajous są czasem wykorzystywane w projektach graficznych jako logo.

Poniżej zamieszczono przykłady krzywych Lissajous o parametrach δ = π / 2 ,a nieparzyste, b parzyste, | a − b | = 1.

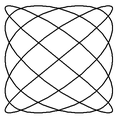
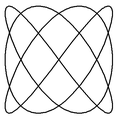
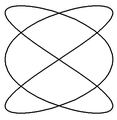
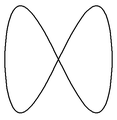
a = 1, b = 2 a = 3, b = 2 a = 3, b = 4 a = 5, b = 4

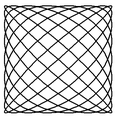
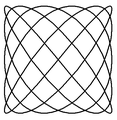
a = 5, b = 6 a = 9, b = 8

Żyroskop

Żyroskop - urządzenie składające się ze sztywnego obiektu wirującego wokół własnej osi, którego oś obrotu może swobodnie zmieniać swoją orientację w przestrzeni.

Własności żyroskopu spełnia wiele ciał np: ciała niebieskie w tym Ziemia, pociski karabinowe (z wyjątkiem wystrzelonych z broni gładkolufowej), wirniki maszyn, koła.

Przyrząd demonstrujący efekty żyroskopowe też jest nazywany żyroskopem, ma on postać metalowego krążka, który raz wprawiony w ruch obrotowy zachowuje swoje pierwotne położenie osi obrotu. Żyroskop został wynaleziony w 1852 przez Leona Foucaulta, jako demonstracja zasady zachowania momentu pędu.

Żyroskopy są używane do budowy żyrokompasów, które mają szerokie zastosowanie w nawigacji, zwłaszcza lotniczej.

Podstawowe równanie opisujące zachowanie żyroskopu:

Zjawisko zmiany położenia osi wirowania żyroskopu pod wpływem działania siły zewnętrznej nazywane jest precesją. Częstość precesji określa wzór:

gdzie:

- moment siły,

- moment pędu żyroskopu,

I - moment bezwładności,

ω - prędkość kątowa,

α - przyspieszenie kątowe,

t - czas,

- częstość precesji.

Warunkiem dobrej pracy żyroskopu jest duża prędkość obrotowa i małe tarcie w łożyskach. Ten drugi cel osiąga się łożyskując żyroskop na strumieniu sprężonego powietrza lub - jeszcze lepiej - "zawieszając" go w polu elektrostatycznym w próżni (wtedy żyroskop o prędkości 24 tys. obr./min wskazuje stały kierunek w przestrzeni z błędem nie większym niż 0,0001°/h, czyli 1° na 14 miesięcy).

Obracające się ciało o ograniczonej swobodzie ruchu osi obrotu to bąk, żyroskop jest też nazywany bąkiem swobodnym.

Dzisiaj żyroskopy stosuje się w urządzeniach do wskazywania wybranego kierunku używanych w samolotach, śmigłowcach, statkach itp. Urządzenie zbudowane na tej zasadzie jest nazywane żyroskopem, żyrokompasem lub kompasem żyroskopowym.

Popęd (fizyka)

Popęd zwany też impuls i popęd siły jest wektorową wielkością fizyczną równą iloczynowi siły i czasu jej działania:

Dla siły zmieniającej się wzór ten można wyrazić:

gdzie

I popęd siły F,

F siła,

t czas.

Jednostką popędu jest N·s = kg·m/s zwany czasami Huygens i oznaczany przez Hy.

Wyprowadzenie [edytuj]

Popęd jest wielkością wprowadzoną do prostego wyrażenia II zasady dynamiki Newtona w prostej postaci. Zmiana pędu ciała jest równa popędowi siły.

7

---