Badanie Interferencji W Doświadczeniu Younga
Wstęp Teoretyczny
Światło cechuje się dualizmem korpuskularno - falowym, co oznacza, że ma zarówno naturę:
fali elektromagnetycznej - potwierdzajÄ… to zjawiska tj.: dyfrakcja i interferencja;
kwantową (światło ma postać kwantów energii) - potwierdzają to zjawiska tj.: termoemisja i efekt Comptona.
Interferencją światła nazywamy nakładanie się dwóch lub więcej wiązek światła (fal poprzecznych) w tym samym obszarze, w wyniku czego wiązki lokalne wzmacniają się lub osłabiają.
Efekt interferencji światła obserwowany na ekranie (albo rejestrowany na kliszy fotograficznej lub powstający na siatkówce oka) nosi nazwę obrazu interferencyjnego. Powstaje on, gdy fale maję stałą w czasie różnicę faz oraz poruszają się w przybliżeniu w tym samym kierunku.
Prążki interfenecyjne to:
jasne pasma - maksima interferencyjne - miejsca wzmocnienia światłą, gdzie energia fal jest maksymalna;
ciemne pasma - minima interferencyjne - miejsca osłabienia światłą, gdzie energia fal jest równa zeru.
Interferencja Å›wiatÅ‚a Å›wiadczy o jego falowej naturze. Wzmacniać siÄ™ i osÅ‚abiać przy spotkaniu ze sobÄ… mogÄ… tylko fale, strumienie zwykÅ‚ych czÄ…stek zawsze „wzmacniajÄ… siÄ™”. Natężenie wypadkowej fali Å›wietlnej, powstaÅ‚ej w wyniku naÅ‚ożenia siÄ™ dwóch fal, zależy od różnicy faz obydwu fal:
jeżeli fazy są zgodne, następuje wzmocnienie,
jeżeli fazy są przeciwne - osłabienie.
Ta zasada interferencji zwana jest zasadÄ… Younga. Young byÅ‚ wÅ‚aÅ›ciwym odkrywcÄ… interferencji Å›wiatÅ‚a i autorem terminu: „interferencja”. W 1802 roku sformuÅ‚owaÅ‚ zasadÄ™ interferencji, która pozwoliÅ‚a mu przeprowadzić sÅ‚ynne doÅ›wiadczenie.
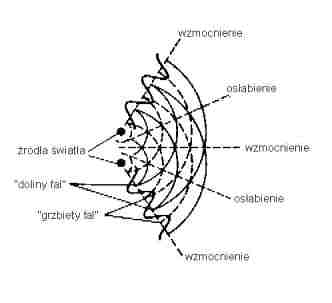
Doświadczenie Younga
Zjawisko ugięcia światła znane było zarówno Huygensowi (1629 - 1695), jak i Newtonowi (1642 - 1727), ale żaden z nich nie umiał z niego skorzystać jako z doświadczalnego kryterium przemawiającego za lub przeciw jego teorii. Dopiero późniejsi badacze, wśród których był również Young zjawisko to zbadali i wyjaśnili.
Wykazanie istnienia interferencji dla światła przez Thomasa Younga w 1801 roku dostarczyło podstawy doświadczalnej dla falowej teorii światła. Young mógł nawet na podstawie swego doświadczenia obliczyć długość fali światła, co było pierwszym pomiarem tej ważnej wielkości.
Young oświetlił światłem słonecznym dwa niewielkie otwory kołowe, co obrazuje rysunek 2.
Ekran „A”, w którym zrobiony byÅ‚ maÅ‚y otworek So. PrzechodzÄ…ce przez ten otworek Å›wiatÅ‚o rozchodzi siÄ™ zgodnie z prawami dyfrakcji i pada na otworki S1 i S2 zrobione w ekranie „B”. Znów nastÄ™puje dyfrakcja i dwie nakÅ‚adajÄ…ce siÄ™ fale kuliste rozchodzÄ… siÄ™ w przestrzeni na prawo od ekranu „B”. Mamy tu do czynienia z optykÄ… falowÄ…, a nie geometrycznÄ….
W wykonywanym przez nas doświadczeniu zamiast otworów kołowych wykorzystaliśmy dwie cienkie szczelinki, które oświetlamy światłem lasera. Schemat ilustruje rysunek 3.
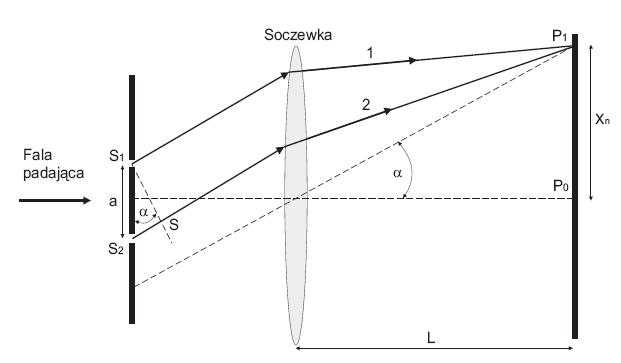
Promień 1 i 2 padając na szczelinki mają taką samą fazę. Promienie padające na soczewkę równolegle do jej głównej osi optycznej skupią się w pkt. P0. Ich różnica dróg optycznych wynosi zero, zatem w tym punkcie powstanie maksimum interferencyjne.
Warunek na maksima i minima wynikający z równania:
dla maksimum różnica dróg optycznych (S2S) równą się parzystej wielokrotności długości fali, zatem warunek przyjmuje postać:
dla minimów różnica dróg optycznych (S2S) równa się nieparzystej wielokrotności połowy długości fali, zatem warunek przyjmuje postać:
Natężenie obrazu interferencyjnego opisuje zależność:
dla λ»d (d - grubość szczelinek)
Natężenia I(α) każdego z maksimów są jednakowe.
dla dowolnych λ i d, biorąc pod
uwagÄ™ dodatkowe efekty dyfrakcyjne,
powstające na każdej ze szczelin
Efekty dyfrakcyjne zmieniają postać funkcji I(α). Maksima zmieniają swoją wartość okresowo malejąc i rosnąc, lecz położenia maksimów i minimów pozostają niemal niezmienione.
Nakładanie się efektu dyfrakcji i interferencji ilustruje poniżej rysunek 4.
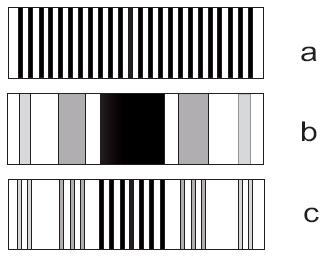
Z geometrii wynika więc:
, gdzie xn to odległość poszczególnych maksimów od środka ekranu.
Ponieważ kąty α są niewielkie to stosuje się przybliżenie: tgα ≈ sinα. Wówczas otrzymujemy:
.
Czyli odległość na ekranie między kolejnymi maksimami interferencyjnymi jest liniową funkcją rzędu maksimum:
, gdzie:
.
Cel Doświadczenia
Celem niniejszego zadania jest zbadanie interferencji na podwójnej szczelinie w doświadczeniu Younga.
Dla zrealizowania powyższego zadania należało połączyć układ pomiarowy, który ilustruje rysunek 5, składający się z:
- dwóch wsporników (2),
- lasera (1),
- przeszkody dla światła laserowego (3).
Opis Czynności Pomiarowych
Po ustawieniu układu w odległości L=132 cm od ekranu i umieszczeniu papieru milimetrowego wykonywaliśmy pomiary przy pomocy slajdów z podwójnymi szczelinami, znajdującymi się w różnej odległości od siebie.
Wyniki pomiarów przedstawiają obrazy wykonane na papierze milimetrowym, które zostały dołączone do sprawozdania.
Opracowanie Wyników Pomiarów
Wnioski
Rys. 3 Schemat interferencji w doświadczeniu Younga
Oznaczenia:
a -odległość między środkami szczelinek
L - odległość soczewki od ekranu
Rys. 5 Schemat układu pomiarowego
Rys. 4 a - obraz interferencyjny
b - obraz dyfrakcyjny (jedna szczelina)
c - nałożenie obu efektów (na dwóch szczelinach)
Rys. 2 Schemat doświadczenia przedstawiający sposób, w jaki Thomas Young wytworzył obraz interferencyjny, przepuszczając światło przez dwa otworki S1 i S2 tak, aby fale ugięte nałożyły się na ekranie C
Rys. 1. Interferencja światła
Wyszukiwarka
Podobne podstrony:
sprawozdanie8 Doświadczenie Younga Natężenie w obrazie dyfrakcyjno interferencyjnym
Doświadczenie younga
doswiadczenie younga3
Doświadczenia biologiczne(1)
Krzywa doświadczeń
Doswiadczenia chemiczne 2
2011 09 22 Rozkaz nr 904 MON instrikcja doświadczenie w SZ RP
doswiadczenia arkusz rs 6 1392900606
DOSWIADCZENIA id 141037 Nieznany
O doświadczalnym wyznaczaniu nośności krytycznej płyt na modelach obarczonych imperfekcjami geome
uzyskiwanie barw eksperyment(1), Doświadczenia(1)
Mikołaja Doświadczyńskiego przypadki, Filologia polska, Oświecenie
Wpływ różnego rodzaju pyłów na wzrost nadziemnej części roślin, referaty i materiały, biologia, dośw
więcej podobnych podstron