STATYSTYKA

STATYSTYKA OPISOWA - to pierwszy krok w analizie danych który pozwala na podsumowanie zbioru danych którymi się zajmujemy i wyciągnięcie podstawowych wniosków i uogólnień na temat tego zbioru

TECHNIKI STATYSTYKI OPISOWEJ:

opis tabelaryczny - dane są przedstawione w tabeli, Jeśli jest ich niewiele to przestawiamy je jako

1. szereg szczegółowy - jeśli jest ich niewiele np. kilkanaście sztuk, to w tabeli są wymiary

wszystkich drzew np. 25,44 cm 23,37 cm itd.

2. szereg rozdzielczy - jeśli jest dużo danych to tworzymy stopnie w których podajemy w

przedziałach ilości sztuk (szacunki)

graficzna prezentacja danych - prezentowane z szeregu rozdzielczego przy pomocy wykresów:

- histogramu (kolumny pionowe na osi x)

- wieloboku liczebności (linia łamana na max wartościach y)

- prezentowane po badaniu statystycznym

- wykresu pudełkowego „ramka - wąsy” z zaznaczeniem

max, min, mediany, kawrteli górnego i dolnego

wyznaczanie miar rozkładu - to różnego rodzaju wielkości obliczane na podstawie uzyskanych

danych tzw cechy dostarczające informacji na temat charakteru jej

rozkładu są to:

• miary położenia (mediana, modalna, średnia arytmetyczna, kwartyl górny, kwartyl dolny)

• miary zmienności = zróżnicowania (rozstęp, odchylenie standardowe, współczynnik zmienności)

• miary asymetrii (skośność)

• miary koncentracji (kurtoza)

SZEREGI STATYSTYCZNE to:

Szereg szczegółowy - zapisane wszystkie pomiary - jak jest niewiele danych w zbiorowości

statystycznej np. kilkanaście

Szereg rozdzielczy - jak dużo danych - prezentowany w formie tabel, uzyskujemy poprzez podział

na kategorie i podajemy liczebność w danej kategorii

(przedziału). Mogą być: jakościowe - strukturalne lub

Ilościowe - punktowe lub przedziałowe

ROZKŁADY EMPIRYCZNE - to przyporządkowanie do odpowiedniej zmiennej „x” odpowiadającej

jej liczebności „n”

typy rozkładów empirycznych

MIARY ROZKŁADU

MIARY POŁOŻENIA = rozkładu

Średnia arytmetyczna - miary średnie pozwalają określić tendencje centralną

To suma wartości wszystkich jednostek podzielona przez ich liczbę

Jest prawidłową miarą tylko mało zróżnicowanych zbiorowości

Nie stosujemy jej dla rozkładów asymetrycznych, bimodalnych i wielomodalnych

Mediana - to wartość dzieląca uporządkowaną zbiorowość na 2 równe części pod względem

liczebności.

Pozycja mediany - to liczba spostrzeżeń + 1 podzielona na połowę Pme = N+1/2

Np. jak 1000 to pozycja = 1001/2 = 500,5

Wartość mediany - to wartość liczby stanowiącej środek zbiorowości - jak nieparzysta

jak parzysta - to wartość jest średnią wartością między środkowymi

liczbami: 11,12,16,25 = wartość mediany = 12+16/2 = 14

Modalna (dominata) - to wartość najczęściej występująca w śród zmiennych „modna”

Np. oceny 3=12 osób, 3,5= 25 osób, 4= 5 osób, 4,5 = 2 osoby modalna - 3,5

Można ją wyznaczyć tylko dla zmiennej typu skokowego, nie można dla

zmiennych typu ciągłego (tu możemy średnią i medianę)

Kwartyle: dolny - przedział w którym 25% obserwacji ma wartość mniejszą, a 75% większą

górny - przedział w którym 75% obserwacji ma wartość mniejszą, a 25% większą

MIARY ZMIENNOŚCI

Rozstęp - różnica między wartością najmniejszą a największą zmiennej

Mała wartość poznawcza bo liczą się tylko dwie wartości często różniące się od

wszystkich pozostałych, obszar między tymi wartościami to obszar zmienności. Może się

przydać jedynie przy wstępnej ocenie rozproszenia

Wariancja - to średnia z kwadratów odchyleń poszczególnych wartości cechy od jej średniej

arytmetycznej

próba: 2 4 6 8 10 wtedy średnia = 30/5 = 6

odchylenie 2-6= -4 4-6= -2 6-6 = 0 8-6= 2 10-6= 4 zawsze daje „0”

kwadrat odchylenia 16 4 0 4 16 suma kwadratów = 40

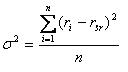
wariancja = 40 (suma kwadratów odchyleń) / 5 (wartości) = 8 cm2

to zawsze liczba nieujemna (bo kwadraty odchyleń)

zawsze wyrażona w jednostkach do kwadratu

czym większa wariancja tym bardziej zróżnicowana zbiorowość

odchylenie standardowe - to pierwiastek kwadratowy z wariancji

dla powyższego przykładu = pierwiastek z 8 cm2 = 2,73cm

określa o ile wszystkie jednostki z tej zbiorowości różnią się średnio od wartości średniej

arytmetycznej. Czym większe odchylenie standardowe tym większa zmienność

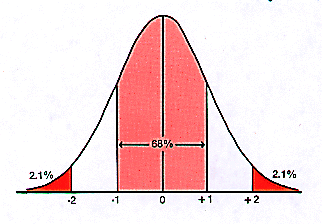
Zazwyczaj mieszczą się one w 2/3 w typowym obszarze zmienności tzn na osi po jednym

odchyleniu na prawo i lewo od średniej

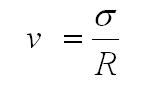
Współczynnik zmienności - to iloraz odchylenia standardowego / i średniej

arytmetycznej

Najczęściej wyrażany w % i zastępuje bezwzględne miary dyspersji (położenia).

Umożliwia dokonywanie analiz w czasie i przestrzeni

Pozwala porównywać zmienność różnych rzeczy np. drzew do pomidorów

MIARY ASYMETRII - określają wewnętrzne zróżnicowanie zbiorowości, przy ich pomocy możemy ocenić czy w zbiorowości więcej jest jednostek powyżej czy poniżej przeciętnej, a także określić charakter (kierunek) oraz jego natężenie (rozmiar)

W praktyce: badania dochodów, absencja chorobowa, wkłady oszczędnościowe

Skośność - im większa tym większe różnice między modalną (dominatą), medianą a średnią

arytmetyczną. Wartość tego współczynnika skośności waha się zazwyczaj od -1 do 1.

W szeregu symetrycznym (skośność = 0) wszystkie te wartości są równe.

Współczynnik skośności = średnia - modalna / odchylenie standardowe

Im silniejsza asymetria rozkładu tym wartość bezwzględna współczynnika skośności

wyższa.

As = 0 As < 0 As > 0

występuje najczęściej w naturze

Kurtoza - określa miarę skupienia wartości wokół średniej

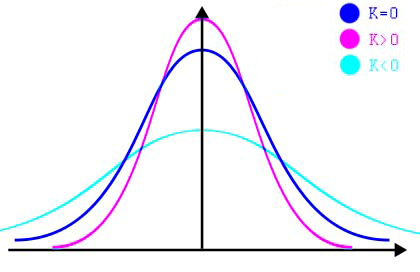
K>0 = większa koncentracja wokół średniej = mała zmienność

K<0 = mniejsza koncentracja wokół średniej = duża zmienność

---