Darrieus wind turbine

From Wikipedia, the free encyclopedia

  (Redirected from Giromill)

Jump to: navigation, search

Fig. 1: A Darrieus wind turbine once used to generate electricity on the Magdalen Islands

The Darrieus wind turbine is a type of vertical axis wind turbine (VAWT) used to generate electricity from the energy carried in the wind. The turbine consists of a number of aerofoils vertically mounted on a rotating shaft or framework. This design of wind turbine was patented by Georges Jean Marie Darrieus, a French aeronautical engineer in 1931.

The Darrieus type is theoretically just as efficient as the propeller type if wind speed is constant, but in practice this efficiency is rarely realised due to the physical stresses and limitations imposed by a practical design and wind speed variation. There are also major difficulties in protecting the Darrieus turbine from extreme wind conditions and in making it self-starting.

Contents [hide] 1 How it works 2 Giromills 3 Cycloturbines 4 Helical blades 5 External links

[edit] How it works

In the original versions of the Darrieus design, the aerofoils are arranged so that they are symmetrical and have zero rigging angle, that is, the angle that the aerofoils are set relative to the structure on which they are mounted. This arrangement is equally effective no matter which direction the wind is blowing -- in contrast to the conventional type, which must be rotated to face into the wind.

When the Darrieus rotor is spinning, the aerofoils are moving forward through the air in a circular path. Relative to the blade, this oncoming airflow is added vectorially to the wind, so that the resultant airflow creates a varying small positive angle of attack (AoA) to the blade. This generates a net force pointing obliquely forwards along a certain 'line-of-action'. This force can be projected inwards past the turbine axis at a certain distance, giving a positive torque to the shaft, thus helping it to rotate in the direction it is already travelling in. Aerodynamics which rotates rotor is equivalent to autogiros and normal helicopters in autorotation.

As the aerofoil moves around the back of the apparatus, the angle of attack changes to the opposite sign, but the generated force is still obliquely in the direction of rotation, because the wings are symmetrical and the rigging angle is zero. The rotor spins at a rate unrelated to the windspeed, and usually many times faster. The energy arising from the torque and speed may be extracted and converted into useful power by using an electrical generator.

The aeronautical terms lift and drag are, strictly speaking, forces across and along the approaching net relative airflow respectively, so they are not useful here. We really want to know the tangential force pulling the blade around, and the radial force acting against the bearings.

When the rotor is stationary, no net rotational force arises, even if the wind speed rises quite high -- the rotor must already be spinning to generate torque. Thus the design is not normally self starting. It should be noted though, that under extremely rare conditions, Darrieus rotors can self-start, so some form of brake is required to hold it when stopped.

One problem with the design is that the angle of attack changes as the turbine spins, so each blade generates its maximum torque at two points on its cycle (front and back of the turbine). This leads to a sinusoidal (pulsing) power cycle that complicates design. In particular, almost all Darrieus turbines have resonant modes where, at a particular rotational speed, the pulsing is at a natural frequency of the blades that can cause them to (eventually) break. For this reason, most Darrieus turbines have mechanical brakes or other speed control devices to keep the turbine from spinning at these speeds for any lengthy period of time.

Another problem arises because the majority of the mass of the rotating mechanism is at the periphery rather than at the hub, as it is with a propeller. This leads to very high centrifugal stresses on the mechanism, which must be stronger and heavier than otherwise to withstand them. One common approach to minimise this is to curve the wings into an "egg-beater" shape (this is called a "troposkein" shape, derived from the Greek for "the shape of a spun rope") such that they are self supporting and do not require such heavy supports and mountings. See. Fig. 1.

In this configuration, the Darrieus design is theoretically less expensive than a conventional type, as most of the stress is in the blades which torque against the generator located at the bottom of the turbine. The only forces that need to be balanced out vertically are the compression load due to the blades flexing outward (thus attempting to "squeeze" the tower), and the wind force trying to blow the whole turbine over, half of which is transmitted to the bottom and the other half of which can easily be offset with guy wires.

By contrast, a conventional design has all of the force of the wind attempting to push the tower over at the top, where the main bearing is located. Additionally, one cannot easily use guy wires to offset this load, because the propeller spins both above and below the top of the tower. Thus the conventional design requires a strong tower that grows dramatically with the size of the propeller. Modern designs can compensate most tower loads of that variable speed and variable pitch.

In overall comparison, while there are some advantages in Darrieus design there are many more disadvantages, especially with bigger machines in MW class. The Darrieus design uses much more expensive material in blades while most of the blade is too near of ground to give any real power. Traditional designs assume that wing tip is at least 40m from ground at lowest point to maximize energy production and life time. So far there is no known material (not even carbon fiber) which can meet cyclic load requirements.

[edit] Giromills

Fig 2: A Giromill-type wind turbine

Darrieus's 1927 patent also covered practically any possible arrangement using vertical airfoils. One of the more common types is the Giromill or H-bar design, in which the long "egg beater" blades of the common Darrieus design are replaced with straight vertical blade sections attached to the central tower with horizontal supports. The Giromill blade design is much simpler to build, but puts more weight into the structure as opposed to blades, and also means that the blades themselves have to be stronger for the reasons outlined above.

[edit] Cycloturbines

Another variation of the Giromill is the Cycloturbine, in which the blades are mounted so they can rotate around their vertical axis. This allows the blades to be "pitched" so that they always have some angle of attack relative to the wind. The main advantage to this design is that the torque generated remains almost constant over a fairly wide angle, so a Cycloturbine with three or four blades has a fairly constant torque. Over this range of angles, the torque itself is near the maximum possible, meaning that the system also generates more power. The Cycloturbine also has the advantage of being able to self start, by pitching the "downwind moving" blade flat to the wind to generate drag and start the turbine spinning at a low speed. On the downside, the blade pitching mechanism is complex and generally heavy, and some sort of wind-direction sensor needs to be added in order to pitch the blades properly.

Fig 3: Schematic of mass-stabilised pitch control system.

A schematic of a self-acting pitch control system that does not require a wind-direction system is shown in Figure 3.

[edit] Helical blades

The blades of a Darrieus turbine can be canted into a helix, e.g. three blades and a helical twist of 60 degrees, similar to Gorlov's water turbines. Since the wind pulls each blade around on both the windward and leeward sides of the turbine, this feature spreads the torque evenly over the entire revolution, thus preventing destructive pulsations. The skewed leading edges reduce resistance to rotation; by providing a second turbine above the first, with oppositely directed helices, the axial wind-forces cancel, thereby minimizing wear on the shaft bearings. Another advantage is that the blades generate torque well from upward-slanting airflow, such as occurs above roofs and cliffs. This design is used by the Turby and Quiet Revolution brand of wind turbine.

[edit] External links

• What Are Vertical-Axis Wind Turbines (VAWTs)?

• Bibliography of VAWT-related papers

• Three Pitch Control Systems for Vertical Axis Wind Turbines Compared - L. Lazauskas

• Experimental Verification of a Mathematical Model for Predicting the Performance of a Self-acting Variable Pitch Vertical Axis Wind Turbines - B.K. Kirke and L. Lazauskas

• US patent 1,835,018

Retrieved from "http://en.wikipedia.org/wiki/Darrieus_wind_turbine#Giromills"

Categories: Vertical axis wind turbines

What is a Darrieus Machine?

A Darrieus machine, a VAWT, is a vertical axis wind turbine. It acts much like a windmill except that a windmill has a horizontal axis. Here are images of Darrieus Machines and derivatives.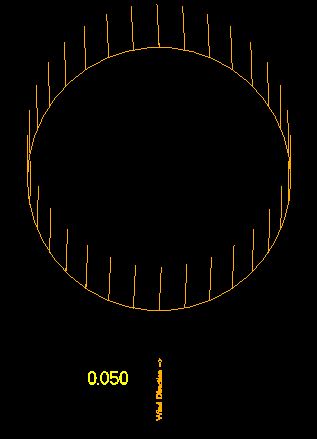





Some Conventions:

Wind is blowing up.
Rotation of the machine is clockwize.

To the right is a simulation of the localized flow at specific points along the periphera of the Darrieus machine. It is animated to show how the flow changes with different rotational speed per wind speed, which is the number in the lower right corner.

basically I used a speed triangle to create this analysis. The rotor has a given tangential speed for a certain RPM, and I vary the wind speed. This gives rise to a couple interesting points:

• Maximum speed is obtained at the 3 O'Clock position. Following, minimum speed occurs at the 9 O'Clock position.

• There is a singularity point at 9 O'Clock.

• For a fixed blade angle, Angle of attack is continuously varying between 90 degrees and 0 degrees.

Interestingly enough, a Darrieus machine used an eliptical blade that has a fixed angle of attack of 0 degrees. This is why a Darrieus machine is not self starting. With a blade angle of 0 degrees, Lift is always directly through the axis of the machine. Only when the machine is spinning can a positive torque be created.

Lets take for example a couple of specific speed ratios. Lets start with rotational speed vs. wind speed of .75.

Looking between 9:00 and 12:00, You can see that if we have a fixed angle of attack of 0 degrees, the angle of attack is almost 90 degrees, so we are making almost no force. The only thing we are creating is a lot of drag, but in this case, drag is helpful.

In the next quadrant (between 12:00 and 3:00), the angle of local flow goes between 45 degrees and 0 degrees. Here we can create some useful lift. With flow averaging about 20 degrees angle of attack, with an elipse as an airfoil we can get some good lift. Now, IANAAE¹, but what happens is that the turbulent airflow on the outside surface creates enough of a boundry layer that we get an effective airfoil shape that has a negative angle of attack (it is pointed inward). so we not only get lift, but the lift is pointed in the propper direction.

In the third quadrant (3:00 to 6:00), we have the same effect. The effective airfoil has a negative angle of attack, which produces a torque about the center axis of the machine.

Fourth Quadrant. Angle of attack goes from 45 degrees to 90 degrees. What really is interesting here is what happens at exactly 90 degrees. If you compair the stream here (directly up) with a flow at a ratio above 1, you will see that the flow instentaneously changes. At a ratio of exactly 1, the relative wind magnitude is exactly zero. Since we are below a ratio of 1, the relative wind is still vaguely in the direction of the real wind, so we would be better off increasing drag (rather than relying on lift) through this quadrant.

So that is it. One cycle in a Darrieus machine.

Now lets take a look at a more advanced flow. With a rotational speed vs wind speed of 1.10, we see a slightly different picture. Quadrants 2 and 3 are very similar. ####, all the quadrants are similar. But look at 9:00. Notice it is pointing down. Notice that the stream line below 9:00 is pointing in the opposite direction of the same stream line for .75. We have a flow reversal somewhere along there.

At this point (9:00) it doesn't make too much sense to become a drag device. if you did, you would actually accelerate the air at 9 O'Clock! So the conclusion is that if you make a drag device you are never going to exceed a ratio of 1.

So Radius is governed by nominal wind speed. Increased windspeed matches increased radius with a constant rotational speed (keeping the ratio to 1). Of course, Power increases linearly with radius (and height too).

Things to do:

• I am not sure what the big boys ratio works out to, but I will find out. generally 5-7

• To do a torque/phase/ratio surface, I need to know stall angles and lift coefficients for an ellipse. (it's the next step up from a torque/phase curve)
  looks like an ellipse stalls at 10 degrees angle of attack and a 1 foot cord, 6 foot long blade will generate about 34 lbs of lift at 42 mph. aim for a thickness about 20% chord width. (a flat plate will do about 29 lbs of lift under the same conditions... is it worth it?

I'd also like to think about making a Darrieus machine that keeps a constant angle of attack. But to do it mechanically means that it is a semi-drag device (it goes into drag mode at 9:00). Which is yet another thing that I am going to need to learn some more numerical controls for.

Why did I do this?
I think Darrieus Machines look cool.

-James

---