Agnieszka Magiera Ewelina Zielińska

Sprawozdanie nr 9 - Konduktometryczne wyznaczanie stałej dysocjacji

1. Wstęp teoretyczny

Słaby jednoprotonowy kwas HA dysocjuje zgodnie z równaniem:

Równowaga tej reakcji zgodnie z prawem działania mas opisywana jest następującym równaniem:

Uwzględniając stopień dysocjacji α, stężenia poszczególnych składników roztworu można wyrazić jako część całkowitego stężenia kwasu c:

Po wstawieniu powyższych równań do równania i uproszczeniu otrzymujemy równanie opisujące prawo rozcieńczeń Ostwalda:

Stopień dysocjacji α można wyrazić jako stosunek przewodnictwa równoważnikowego λ danego elektrolitu do jego granicznego przewodnictwa równoważnikowego λ^∞ (postulat Arrheniusa):

Po przekształceniu otrzymujemy równanie opisujące stałą dysocjacji K_a słabego kwasu z wykorzystaniem przewodnictwa równoważnikowego:

Dalsze przekształcenie prowadzi do równania o następującej formie:

Równanie to jest równaniem prostej typu
:

Po zmierzeniu przewodnictwa właściwego κ roztworu słabego kwasu dla różnych stężeń c można wyliczyć przewodnictwo równoważnikowe roztworu λ. Z wykresu funkcji 1/λ = f(cλ) w pierwszej kolejności wyznacza się λ^∞ (z przecięcia prostej z osią y przy zerowej wartości na osi x), a następnie z nachylenia prostej stałą dysocjacji K_a.

2. Obliczenia

1. Obliczyłyśmy ze wzoru
   stałą oporową sondy, gdzie:

S - przewodnictwo roztworu wzorcowego zmierzonego przez nas S=

H - przewodnictwo właściwe substancji wzorcowej (KCl), wartość tablicowa H= 0,0012211

2. Wyliczyłyśmy, korzystając z wcześniejszego wzoru, przewodnictwo badanych roztworów dla wszystkich stężeń:

Dla poszczególnych stężeń danych substancji, z wyznaczoną przez nas przewodnością na zajęciach, sporządziłyśmy tabelę, w której umieściłyśmy obliczone za pomocą powyższego wzoru przewodnictwa właściwe:

co	CH3COOH		CH3COONa		HCl		NaCl
		S [mS]	H[ ]	S [mS]	H[ ]	S [mS]	H[ ]	S [mS]	H[ ]
1/16	0,35	4,55
1/32	0,22	2,86	1,87	24,3	9,90	128,70	2,77	36,0
1/64	0,16	2,08	1,04	13,5	5,13	66,69	1,44	18,7
1/128	0,12	1,56	0,54	7,0	2,57	33,41	0,73	9,5
1/256	0,08	1,04	0,32	4,2	1,29	16,77	0,37	4,8
1/512	0,05	0,65	0,17	2,2	0,65	8,45	0,19	2,5
1/1014	0,03	0,39	0,10	1,3	0,33	4,29	0,10	1,3

3. Korzystając z poniższego wzoru obliczyłyśmy dla wszystkich pomiarów wartości λ.

, gdzie:

c - stężenie roztworu

H - przewodnictwo właściwe

Jeżeli:

a:

wtedy:

gdzie 1000 oznacza 1000cm³ na 1dm³

stąd:

(Jednostki tej nie umieszczamy w tabeli poniżej, bo zajmowała ona zbyt dużo miejsca w kolumnach).

Wyniki umieściłyśmy w tabeli niżej, zestawiając w niej wcześniej obliczone przez nas wielkości.

co [M]	CH3COOH			CH3COONa			HCl			NaCl
		S [mS]	H[ ]	λ	S [mS]	H[ ]	λ	S [mS]	H[ ]	λ	S [mS]	H[ ]	λ
1/16	0,35	4,55	7,2800
1/32	0,22	2,86	9,1520	1,87	24,3	77,7920	9,90	128,70	411,840	2,77	36,0	115,232
1/64	0,16	2,08	13,3120	1,04	13,5	86,5280	5,13	66,69	426,816	1,44	18,7	119,808
1/128	0,12	1,56	19,9680	0,54	7,0	89,8560	2,57	33,41	427,648	0,73	9,5	121,472
1/256	0,08	1,04	26,6240	0,32	4,2	106,4960	1,29	16,77	429,312	0,37	4,8	123,136
1/512	0,05	0,65	33,2800	0,17	2,2	113,1520	0,65	8,45	432,640	0,19	2,5	126,464
1/1024	0,03	0,39	39,9360	0,10	1,3	133,1200	0,33	4,29	439,296	0,10	1,3	133,120

4. Wykonałyśmy wykres zależności
   dla roztworów badanych i ekstrapolowałyśmy graficznie powyższą funkcję do
   by wyznaczyć wartości przewodnictwa granicznego mocnych elektrolitów.

Poniżej umieściłyśmy pomocniczą tabelę:

	co [M]	CH3COOH	CH3COONa	HCl	NaCl
				λ	λ	λ	λ
0,2500	1/16	7,2800
0,1768	1/32	9,1520	77,7920	411,840	115,232
0,1250	1/64	13,3120	86,5280	426,816	119,808
0,0884	1/128	19,9680	89,8560	427,648	121,472
0,0625	1/256	26,6240	106,4960	429,312	123,136
0,0442	1/512	33,2800	113,1520	432,640	126,464
0,0313	1/1024	39,9360	133,1200	439,296	133,120

5. Obliczyłyśmy przewodnictwo graniczne słabego kwasu korzystając ze wzoru
   

6. Na podstawie wzoru
   obliczyłyśmy stałe dysocjacji słabego kwasu dla wszystkich stężeń, gdzie:

α - stopień dysocjacji elektrolitu,

K_dys - stała dysocjacji elektrolitu

c₀ - stężenie początkowe elektrolitu

Wyniki zamieściłyśmy w tabeli:

co [M]	K
1/16	2,7080
1/32	1,3540
1/64	0,6770
1/128	0,3385
1/256	0,1693
1/512	0,0846
1/1024	0,0423

Obliczamy wartość średnią stałej dysocjacji, jej średni błąd kwadratowy i odchylenie standardowe:

Wartość średnia stałej dysocjacji wynosi : 7,677

Odchylenie standardowe wynosi: 9,706

Średni błąd kwadratowy średniej aryt. wynosi: 3,962

Wartość średnia stałej dysocjacji po uwzględnieniu odchylenia standardowego zgadza się z wartością tablicową:

7. 
   Wykonałyśmy wykres zależności
   i obliczyłyśmy z wykresu stałą dysocjacji kwasu korzystając z zależności
   . Następnie porównałyśmy wartość przez nas uzyskaną z otrzymaną z wykresu oraz z wartością literaturową.

Poniżej prezentujemy pomocniczą tabelę, która posłużyła nam do sporządzenia wykresu:

λ	c	1/ λ	c* λ
7,2800	0,0625	0,1374	0,455
9,1520	0,0312	0,1093	0,286
13,3120	0,0156	0,0751	0,208
19,9680	0,0078	0,0501	0,156
26,6240	0,0039	0,0376	0,104
33,2800	0,0020	0,0301	0,065
39,9360	0,0010	0,0251	0,039

Równanie to jest równaniem prostej typu

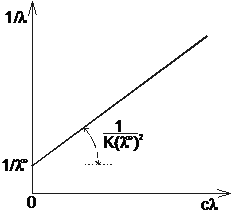
Korzystając z regresji liniowej wyliczyłyśmy współczynnik korelacji, współczynnik kierunkowy a oraz wyraz wolny b:

a=0,291 i b=0,012

r=0,97 - tak duża wartość współczynnika korelacji świadczy o zależności liniowej

Wiedząc, że:

oraz
otrzymujemy:

Wartość tablicowa wynosi:

Błąd względny wynosi:

Odchylenie standardowe wartości współczynnika kierunkowego wynosi S_a= 0,023.

3. Wnioski

W przypadku mocnych elektrolitów, takich jak HCl i NaCl oraz CH₃COONa zależność opisana wzorem Kohlrauscha jest prostoliniowa i umożliwia wyznaczanie granicznej przewodności molowej na drodze ekstrapolacji. Dla elektrolitów słabych, takich jak CH₃COOH, zależność Kohlrauscha nie jest już liniowa, dlatego ekstrapolacji dla elektrolitów słabych nie można dokonać. Dla tych elektrolitów przewodnictwo równoważnikowe wzrasta gwałtownie, gdy stężenie zmierza do zera (krzywa zbliża się asymptotycznie do osi rzędnych nie przecinając jej). Wartość granicznej przewodności mogłyśmy obliczyć korzystając z prawa niezależnego ruchu jonów Kohlrauscha poprzez zsumowanie stałych udziałów jonowych. Nasze doświadczenie i wykonane przez nas obliczenia dowodzą prawdziwości tej teorii.

Jak widać na wykresach przez nas sporządzonych, w obszarze niskich stężeń dla obu grup elektrolitów - i słabych, i mocnych - obserwujemy monotoniczny spadek przewodności molowej ze stężeniem. Jest on jednak znacznie szybszy dla elektrolitów słabych - już dla roztworów średnio stężonych wartości przewodności są niskie. Wytłumaczeniem tego faktu jest zmniejszanie się stopnia dysocjacji ze wzrostem stężenia. Wpływ wzrostu stężenia roztworów silnych elektrolitów na spadek wartości przewodności jest znacznie słabszy, bo w obszarze wysokich stężeń wartość przewodności dla mocnych elektrolitów pozostaje na znaczącym poziomie - mocne elektrolity są w roztworze praktycznie całkowicie zdysocjowane.

Otrzymane przez nas wartości dowodzą, że założenie Arrheniusa dotyczące braku wpływu stężenia na ruchliwość jonów jest wystarczające - obliczona przez nas stała dysocjacji jest bardzo zbliżona do wartości tablicowej. Prawo rozcieńczeń Ostwalda, z którego korzystałyśmy, pozwoliło nam sprawdzić, że słuszne są założenia klasycznej teorii dysocjacji elektrolitycznej. Obliczona przez nas stała dysocjacji w granicach błędu również zgadza się z wartością tablicową.

---