1.Wyliczenie siły potrzebnej do utrzymania klapy w zamknięciu.

1.1 Wykres parcia (Rys.1)

h₁= 1,45 m d₁=1,2m

h₂= 3,2 m d₃=1,2 m

h₃= 1,9 m

b= 1,0 m

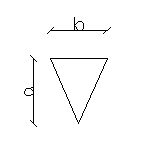
1.2 Schemat przegrody

1.3 Obliczenie sił parcia hydrostatycznego wody na ściany zbiornika.

h₁= 1,45 m d₁=1,2m

h₂= 3,2 m d₃=1,2 m

h₃= 1,9 m

b= 1,2 m

γ = 10 kN/m³

1. Rzędne parcia w punktach charakterystycznych.

γ ⋅ h₁ = 10 kN/m³ ⋅ 1,45 m = 14,5 kPa

γ ⋅ (h₁+h₂ ) = 10 kN/m³ ⋅ (1,45m +3,2m) = 46,5 kPa

γ ⋅ (h₁+h₂+h₃ ) = 10 kN/m³ ⋅ (1,45m +3,2m + 1,9m) =65,5 kPa

2. Wyliczenie poszczególnych składowych siły parcia hydrostatycznego.

Sposób pierwszy:

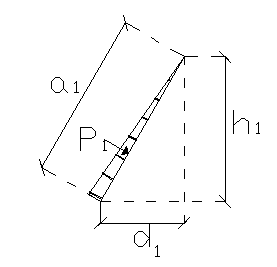
P₁ = 0,5თa₁ თ (ၧ ⋅ h₁) თ b = 0,5 თ1,8821თ (10 თ1,45) თ 1,00 = 13,6452 kN

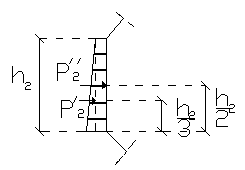
P'₂ = 0,5 თ [ ၧ თ (h₁+h₂) - (ၧთh₁)] · h₂ თ b =

= 0,5 თ [ 10 თ (1,45 + 3,2) - (10 · 1,45)] · 3,2 თ 1,00 = 51,2 kN

P''₂ = (ၧ თ h₁) თ h₂ თ b = (10 kN/m³ თ 1,45m) თ 3,2 თ 1,00 = 46,4 kN

P₂ = P'₂ + P''₂ = 51,2 kN+ 46,4 kN = 97,6 kN

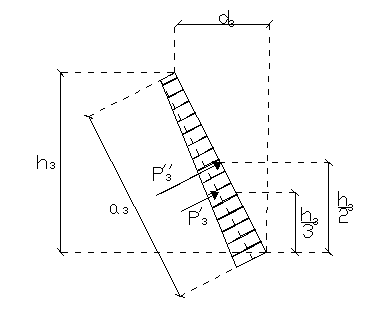
P'₃ = 0,5 თ [ ၧ თ (h₁+h₂+h₃) - ၧ (h₁+h₂) ] თ a₃ თ b =

= 0,5 თ [ 10 თ (1,45 +3,2+1,9) - 10(1,45+3,2) ] თ 2,2472 თ 1,00 = 21,3484 kN

P''₃ = a₃ [ၧ თ (h₁+h₂)] თ b = 2,2472·[10 kN/m³ თ (1,45+3,2)] თ 1,00 = 104,4948 kN

P₃ = P'₃ + P''₃ = 21,3484 kN + 104,4948 kN = 125,8432 kN

Sposób drugi:

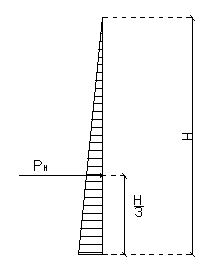
P_H = 0,5 თ [ ၧ თ (h₁+h₂+h₃) ] თ (h₁+h₂+h₃) თ b =

= 0,5 თ [ 10 თ (1,45 + 3,2 + 1,9)] · (1,45 + 3,2 + 1,9) თ 1,00 = 214,51 kN

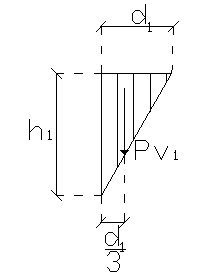
P_V1= 0,5 თ d₁ თ (ၧ თ h₁) თ b = 0,5 თ 1,2 თ (10 თ 1,45) თ 1,00 = 8,7 kN

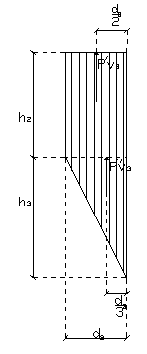
P_V3' =d₃ თ [ ၧ თ (h₁+h₂)] თ b = 1,2 თ [10 თ (1,45 + 3,2)] თ 1,00 = 55,8 kN

P_V3'' = 0,5 თ [ ၧ თ (h₁+h₂+h₃) - ၧ (h₁+h₂)] · d₃ თ b =

= 0,5 თ [ 10 თ (1,45 + 3,2 + 1,9) - 10(1,45+3,2)] · 1,2 · 1,00 = 11,4 kN

P_V3= P_V2'+ P_V2'' = 55,8 kN +11,4 kN = 67,2 kN

3. Sprawdzenie obliczeń

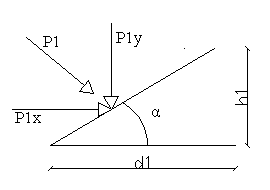
α = arc tg 1,2083 =50,3885°

P₁x = P_1·sinα = 10,5121 kN

P₁y = P_1·cosα = 8,7 kN

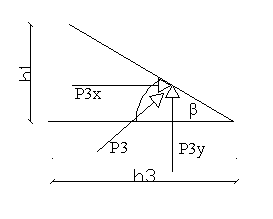
β = arc tg 1,95 =57,7238°

P₃x = P_3·sinβ = 106,3983 kN

P₃y = P_3·cosβ = 67,2004 kN

y: -P₁y + P₃y = -Pv₁ + Pv₃ L=P dopuszczalny błąd: ±0,05

-8,7 + 67,2004 = -8,7+67,2

58,5004 = 58,5 błąd: 0,0004

x: P₁x +P₂ + P₃x = P_H L=P dopuszczalny błąd: ±0,05

10,5121 + 97,6 + 106,3983 = 296,45

214,5104 =214,51 błąd: 0,0004

1.4 Obliczenie siły F

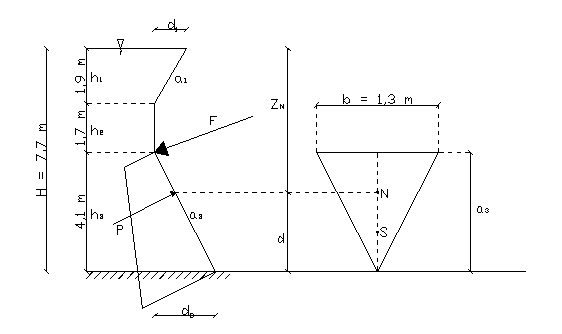
1. Parcie hydrostatyczne

P=
59,3635 kN

2. Zagłębienie środka parcia - Z_N

3. Obliczenie siły F potrzebnej do utrzymania w zamknięciu klapy.

H = h₁ + h₂ +h₃ = 6,55 m

d = H - Z_N = 6,55 - 5,318 = 1,232 m

β = 57,7238°

F · a₃ ≥ P · e

F ≥ 38,49 kN

Minimalna siła potrzebna do utrzymania klapy w zamknięciu to 38,49 kN.

2. Sporządzenia wykresu linii ciśnień i energii. ( Rys. 2)

2.1. Założenie Q - przepływu

d₁= 19mm

d₂= 29mm

l₁= 3,9m

l₂= 14,1m

l₃= 2,3m

Zakładam Q = 69,3 [l/min] = 1,155 · 10 ^{- 3} [m³/s]

2.2.Obliczenie prędkości przepływu w przewodzie odpływowym na kolejnych odcinkach dla założonego Q.

d - przekrój przewodu [m]

2.3 Obliczenie liczby Reynolds'a

R_e=

R_e ≤ 2320 → ruch laminarny

R_e > 4000 → ruch turbulentny

2320 < R_e ≤ 4000 → ruch nieustalony

ν = 1,306 · 10 ^{- 6} [m²/s] - kinetyczny współczynnik lepkości, dla wody w temp. 10°C, którą przyjmuje się w Polsce do obliczeń wodociągów.

R_e1=
= 59294 = 5,9294 × 10⁴ → Re₁ > 4000 - przepływ burzliwy

R_e2=
= 38848 = 3,8848 × 10⁴ → 2320 < Re₂ ≤ 4000 - przepływ nieustalony

2.4 Obliczanie chropowatości względnej.

k - chropowatość względna [mm]

d - chropowatość [mm] dla miedzi k = 0,0015 [mm]

2.5 Odczyt współczynnika λ z homogramu współczynników strat energii na długości:

λ₁=0,0218

λ₂=0,0244

λ - współczynnik strat na długości zależny od liczby Reynolds'a i chropowatości

względnej ε

2.6 Ustalenie współczynnika strat miejscowych ξ

1. strata 1 - spowodowana nagłym zmniejszeniem przewodu odpływowego

= 0,2854

2. strata 2 spowodowana załamaniem przewodu odpływowego

dla φ = 15° → ξ₂ = 0,02

3. strata 3 spowodowane wlotem o prostokątnych krawędziach

ξ₃=0,5

2.7 Obliczenie strat energii na długości:

g - przyśpieszenie ziemskie [m²/s]

g = 9,81[m²/s]

L₃- długość przewodu [m]

5,9517m

2.8 Ustalenie strat miejscowych

0,3227m

2.9 Obliczenie wysokości prędkości

wysokość prędkości [m]

α=1,0 - współczynnik Saint - Venanta (1,0 - dla rur)

2.10 Obliczanie wysokości położenia rozpatrywanego przekroju z₁

2.11 Sprawdzanie obliczeń Dopuszczalny błąd ±0,05

1,9 + 1,7 + 4,1 = 5,9517+0,3227+
+0,61628

7,7 = 7,73728

L ≈ P błąd : 0,03728

Projekt nr 1 z hydrauliki i hydrologii

STR. 6

---