2.2 Zestawienie obciążeń stropu

Rodzaj warstwy	Obciążenie charakterystyczne kN/m²	γf	Obciążenie obliczeniowe kN/m²
Płytki lastryko 0,03*22	0,66	1,2	0,792
Gładź cementowa grubości 35mm 0,03*21	0,63	1,3	0,819
Płyta pilśniowa 0,02*5,5	0,11	1,2	0,132
Wylewka betonowa 0,06*24	1,44	1,3	1,872
blacha trapezowa T55 × 188 104,97 kN/m^2	0,22	1,1	0,242
Belka I 340 68,1 kN/m^2	0,668	1,1	0,735
Płyta gipsowo kartonowa 0,015	0,522	1,2	0,626
RAZEM	4,25	-	5,22
Obciążenie zmienne	1,6	1,3	2,08
RAZEM	5,85	-	7,3

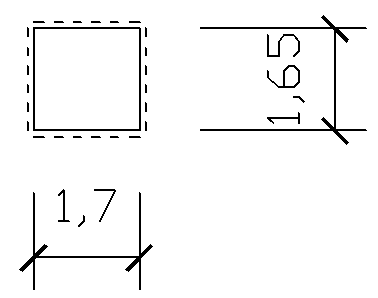
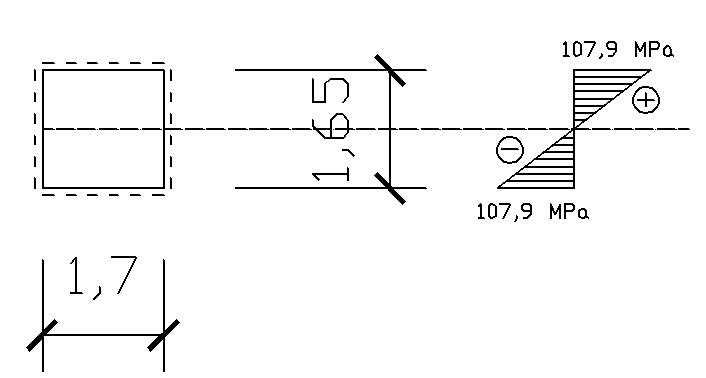
Strop:

-rozstaw belek A-1 (1700mm)

-rozstaw belek A-2 (1500mm)

2.3. Wymiarowanie belki A-1:

Belka będzie wykonana ze stali St3SY o f_d= 215 MPa.

2.3.1 Obliczenia statyczne:

- obliczenie wartości obliczeniowej płyty o rozpiętości belki a=1,7m

g_o = (g + p) · a = 7,3 · 1,7 = 12,41 kN/m

-rozpiętość obliczeniowa dla belki jednostronnie opartej na murze:

l₀=

- wartości maksymalnych sił wewnętrznych wynoszą:

moment zginający

- reakcje podporowe

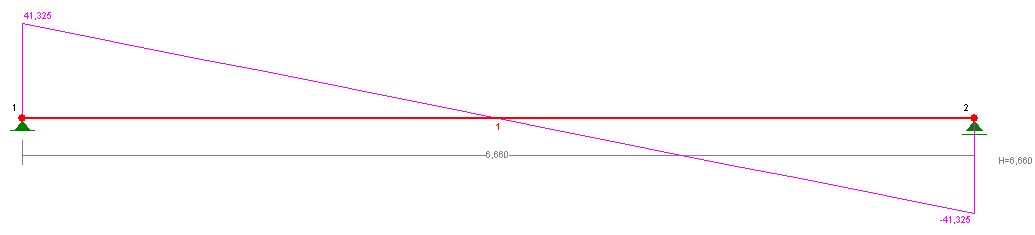
2.3 Obliczenie belki A-1 i A2

2.3.2. Wstępne przyjęcie wymiarów belki.

Założenia:

- belka pracuje w jednoosiowym stanie zginania

- zakładam przekrój klasy 3 ψ=1

- belka zabezpieczona przed zwichrzeniem φ=1

Sprawdzenie nośności elementów jednokierunkowo zginanych:

(wzór 52 normy)

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

M = M_max = 68,81kNm.

Na podstawie przekształcenia wzorów (52) i uwzględniając wzór (42) obliczam niezbędną wielkość wskaźnika przekroju na zginanie W_x:

W_x
W_x
W_x

Wstępnie przyjmuję dwuteownik zwykły I 240 o następujących parametrach:

W_x = 354 cm³ I_x= 4250 cm⁴ I_y=221cm⁴ g=0,37kN/m A= 46,1cm²

2.3.3. Korekta wartości obciążenia obliczeniowego oraz sił wewnętrznych.

g₀ = g₀ + (g · a) = 12,41+
= 12,82 kN/m

2.3.4. Sprawdzenie SGN (Stanu Granicznego Nośności) dla belki A-1:

- wyznaczenie klasy przekroju:

h = 240 mm

b_f = 106 mm

t_f = 13,1 mm

t_w = 8,7 mm

R = 8,7 mm

- klasa środnika (tablica 6 pozycja A normy)

Środnik jest w klasie 1.

- klasa pasów (tablica 6 pozycja b normy):

Pas znajduje się w klasie 1.

Przekrój znajduje się w klasie 1.

2.3.4.1 Sprawdzenie nośności.

Nośność obliczeniowa ścianek ścinanych określana jest wzorem 16 normy :

- współczynnik niestateczności przy ścinaniu

- pole przekroju czynnego przy ścinaniu

f_d - wytrzymałość obliczeniowa stali

Warunek nośności przekroju:

Warunek nośności został spełniony.

2.3.4.2 Sprawdzenie nośności na momenty.

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

M_R=

Warunek nośności przekroju zabezpieczenia przed zwichrzeniem:

Warunek nośności został spełniony.

2.3.5 Sprawdzenie SGU (Stanu Granicznego Użytkowania):

- wartość obciążenia charakterystycznego działającego na belkę:

- obliczenie ugięcia belki

Belka jest jednoprzęsłowa wolnopodparta obciążona w sposób ciągły, przy

obliczaniu ugięcia ze wzoru:

- wartość ugięcia dopuszczalnego

(tablica 4 normy)

Warunek SGU jest spełniony.

Ostatecznie przyjmuje belkę A-1 jako I 240 o parametrach:

Wx = 354 cm³ ; Ix= 4250 cm⁴ ; g=0,37kN/m

2.3.6 Sprawdzenie belki na zwichrzenie w fazie montażu na stropie:

-nie uwzględniam obciążenie zmiennego technologicznie.

lecz:

-cechy geometryczne przekroju I240

J_x= 4250 cm⁴; J_τ= 27,2 cm⁴;

J_y= 221 cm⁴; k= 0,0192 1/cm;

i_x= 9,59 cm; y_s= 0 cm;

i_y= 2,20 cm ; r_x= 0;

W_x= 354 cm³;

W_y= 41,7 cm³;

ω_max = 60,2 cm²;

J_ω= 28500 cm⁶;

W_ω= 473 cm⁴;

a_s= y_s - a₀= 12cm;

b_y= y_s-0,5⋅r_x= 0cm;

- współczynnik długości wyboczeniowej przy wyboczeniu giętnym:

µ_y= 1 (tablica Z1-2);

-współczynnik długości wyboczeniowej przy wyboczeniu skrętnym:

µ_w= 1 (tablica Z1-2);

-obliczenie siły krytycznej przy ściskaniu osiowym:

-obliczenie siły krytycznej przy wyboczeniu skrętnym:

(Z1-5)

-współczynniki pomocnicze:

A₁= 0,61; A₂= 0,53; B= 1,14; C₁= 0,93; C₂= 0,81; (tablica Z1-2)

-moment krytyczny przy zwichrzeniu:

(Z1-9)

-obliczenie nośności przekroju w jednokierunkowym zginaniu

-obliczenie smukłości przy zwichrzeniu:

-odczytanie współczynnika zwichrzenia:

-nośność belki na zginanie:

Belka wymaga zabezpieczenia przed zwichrzeniem.

Metoda uproszczona:

1,53 > 1

Belka wymaga zabezpieczenia przed zwichrzeniem.

2.4 Wymiarowanie belki A-2:

Belka będzie wykonana ze stali St3SY o f_d= 215 MPa.

2.4.1 Obliczenia statyczne:

- obliczenie wartości obliczeniowej płyty o rozpiętości belki a=1,5m

g_o = (g + p) · a = 7,3 · 1,5 = 10,95 kN/m

-rozpiętość obliczeniowa dla belki jednostronnie opartej na murze:

l₀=

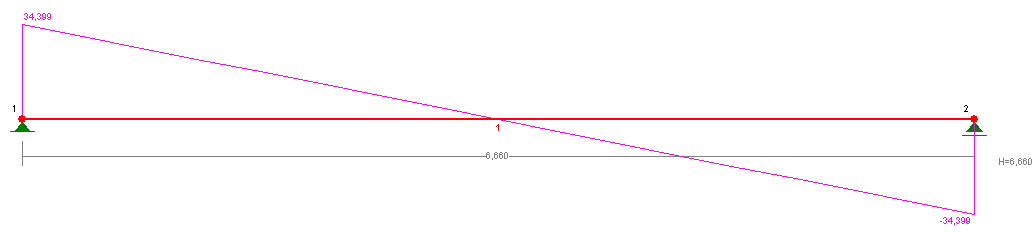
- wartości maksymalnych sił wewnętrznych wynoszą:

moment zginający

- reakcje podporowe

2.4.2. Wstępne przyjęcie wymiarów belki.

Założenia:

- belka pracuje w jednoosiowym stanie zginania

- zakładam przekrój klasy 3 ψ=1

- belka zabezpieczona przed zwichrzeniem φ=1

Sprawdzenie nośności elementów jednokierunkowo zginanych:

(wzór 52 normy)

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

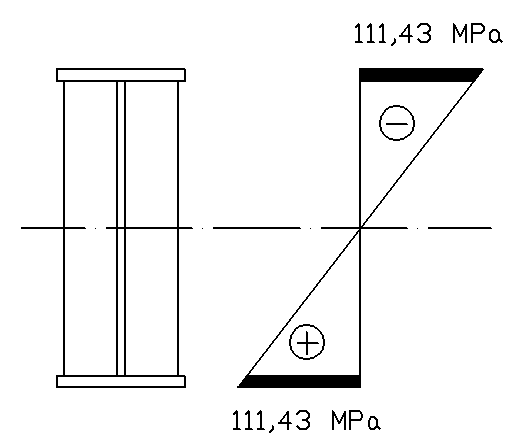
M = M_max = 60,71kNm.

Na podstawie przekształcenia wzorów (52) i uwzględniając wzór (42) obliczam niezbędną wielkość wskaźnika przekroju na zginanie W_x:

W_x
W_x
W

Wstępnie przyjmuję dwuteownik zwykły I 240 o następujących parametrach:

W_x = 354 cm³ I_x= 4250 cm⁴ I_y=221cm⁴ g=0,37kN/m A= 46,1cm²

2.4.3. Korekta wartości obciążenia obliczeniowego oraz sił wewnętrznych.

g₀ = g₀ + (g · a) = 10,95+
= 11,36 kN/m

2.4.4. Sprawdzenie SGN (Stanu Granicznego Nośności) dla belki A-2:

- wyznaczenie klasy przekroju:

h = 240 mm

b_f = 106 mm

t_f = 13,1 mm

t_w = 8,7 mm

R = 8,7 mm

- klasa środnika (tablica 6 pozycja A normy)

Środnik jest w klasie 1.

- klasa pasów (tablica 6 pozycja b normy):

Pas znajduje się w klasie 1.

Przekrój znajduje się w klasie 1.

2.3.4.1 Sprawdzenie nośności.

Nośność obliczeniowa ścianek ścinanych określana jest wzorem 16 normy :

- współczynnik niestateczności przy ścinaniu

- pole przekroju czynnego przy ścinaniu

f_d - wytrzymałość obliczeniowa stali

Warunek nośności przekroju:

Warunek nośności został spełniony.

2.4.4.2 Sprawdzenie nośności na momenty.

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

M_R=

Warunek nośności przekroju zabezpieczenia przed zwichrzeniem:

Warunek nośności został spełniony.

2.4.5 Sprawdzenie SGU (Stanu Granicznego Użytkowania):

- wartość obciążenia charakterystycznego działającego na belkę:

- obliczenie ugięcia belki

Belka jest jednoprzęsłowa wolnopodparta obciążona w sposób ciągły, przy

obliczaniu ugięcia ze wzoru:

- wartość ugięcia dopuszczalnego

(tablica 4 normy)

Warunek SGU jest spełniony.

Ostatecznie przyjmuje belkę A-2 jako I 240 o parametrach:

Wx = 354 cm³ ; Ix= 4250 cm⁴ ; g=0,37kN/m

2.3.6 Sprawdzenie belki na zwichrzenie w fazie montażu na stropie:

-nie uwzględniam obciążenie zmiennego technologicznie.

lecz:

-cechy geometryczne przekroju I240

J_x= 4250 cm⁴; J_τ= 27,2 cm⁴;

J_y= 221 cm⁴; k= 0,0192 1/cm;

i_x= 9,59 cm; y_s= 0 cm;

i_y= 2,20 cm ; r_x= 0;

W_x= 354 cm³;

W_y= 41,7 cm³;

ω_max = 60,2 cm²;

J_ω= 28500 cm⁶;

W_ω= 473 cm⁴;

a_s= y_s - a₀= 12cm;

b_y= y_s-0,5⋅r_x= 0cm;

- współczynnik długości wyboczeniowej przy wyboczeniu giętnym:

µ_y= 1 (tablica Z1-2);

-współczynnik długości wyboczeniowej przy wyboczeniu skrętnym:

µ_w= 1 (tablica Z1-2);

-obliczenie siły krytycznej przy ściskaniu osiowym:

-obliczenie siły krytycznej przy wyboczeniu skrętnym:

(Z1-5)

-współczynniki pomocnicze:

A₁= 0,61; A₂= 0,53; B= 1,14; C₁= 0,93; C₂= 0,81; (tablica Z1-2)

-moment krytyczny przy zwichrzeniu:

(Z1-9)

-obliczenie nośności przekroju w jednokierunkowym zginaniu

-obliczenie smukłości przy zwichrzeniu:

-odczytanie współczynnika zwichrzenia:

-nośność belki na zginanie:

Belka wymaga zabezpieczenia przed zwichrzeniem.

2.5 Wymiarowanie belki A-3

Belka będzie wykonana ze stali St3SY o f_d= 215 MPa.

2.5.1 Obliczenia statyczne:

- obliczenie wartości obliczeniowej płyty (belka oparta jednostronnie na

murze) o rozpiętości belki a=1,7m:

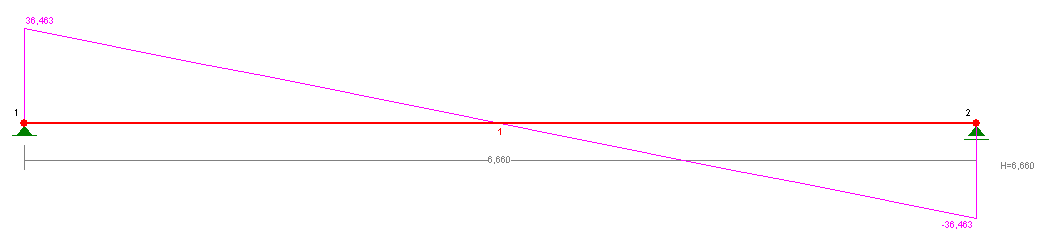
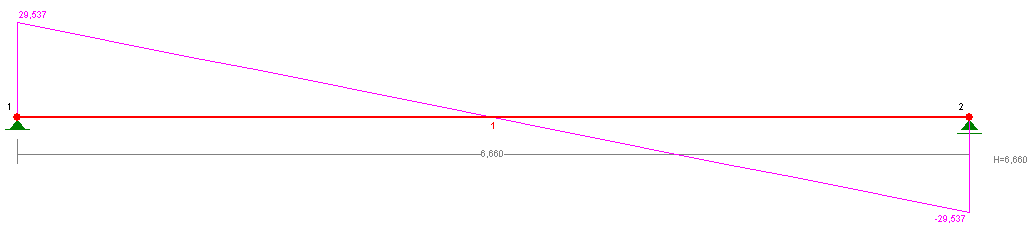
g₀ = (g + p) · 1,7⋅0,5 = 7,3 · 1,7⋅0,5= 6,21 kN/m.

R_A-2=37,83 kN

Rozpiętość obliczeniowa dla belki jednoprzęsłowej wynosi:

l₀=

- obliczenia statyczne wykonane przy pomocy programu „RM-Win­_4.21”

Schemat:

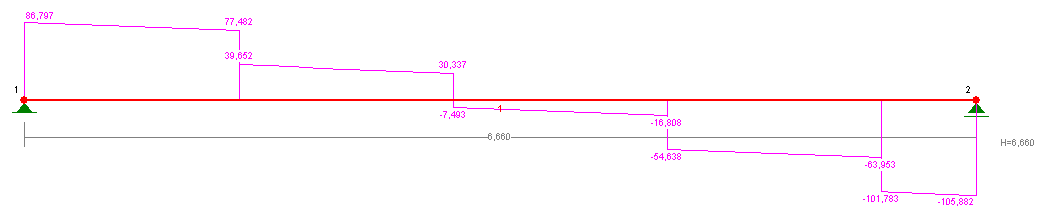
2.5.2. Wstępne przyjęcie wymiarów belki.

Założenia:

- belka pracuje w jednoosiowym stanie zginania

- zakładam przekrój klasy 3 ψ=1

- belka zabezpieczona przed zwichrzeniem φ=1

Sprawdzenie nośności elementów jednokierunkowo zginanych:

wzór 52 normy

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

M = M_max = 175,7 kNm.

Na podstawie przekształcenia wzorów (52) i uwzględniając wzór (42) obliczam niezbędna wielkość wskaźnika przekroju na zginanie W_x:

W_x
W_x
W_x
= 817,2 cm³

Wstępnie przyjmuję dwuteownik zwykły I 340 o następujących parametrach:

Wx = 923 cm³ Ix= 15700 cm⁴ I_y=674cm⁴ g=0,69kN/m A= 86,8cm²

2.5.3. Korekta wartości obciążenia obliczeniowego oraz sił wewnętrznych.

g₀ = g₀ + (g · a) = 6,21+0,69⋅1,1= 6,97 kN/m

2.5.4. Sprawdzenie SGN (Stanu Granicznego Nośności) dla belki A-3:

- wyznaczenie klasy przekroju:

h = 340 mm

b_f = 137 mm

t_f = 18,3 mm

t_w = 12,2 mm

R = 12,2 mm

- klasa środnika (tablica 6 pozycja A normy)

Środnik jest w klasie 1.

- klasa pasów (tablica 6 pozycja b normy):

Pas znajduje się w klasie 1.

Przekrój znajduje się w klasie 1.

2.4.4.1 Sprawdzenie nośności.

Nośność obliczeniowa ścianek ścinanych określana jest wzorem 16 normy :

- współczynnik niestateczności przy ścinaniu

- pole przekroju czynnego przy ścinaniu

f_d - wytrzymałość obliczeniowa stali

Warunek nośności przekroju:

Warunek nośności został spełniony.

2.5.4.2 Sprawdzenie nośności na momenty.

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

M_R=

Warunek nośności przekroju zabezpieczenia przed zwichrzeniem:

Warunek nośności został spełniony.

2.5.5 Sprawdzenie SGU (Stanu Granicznego Użytkowania):

- wartość obciążenia charakterystycznego działającego na belkę:

R_A-2k=37,83 kN

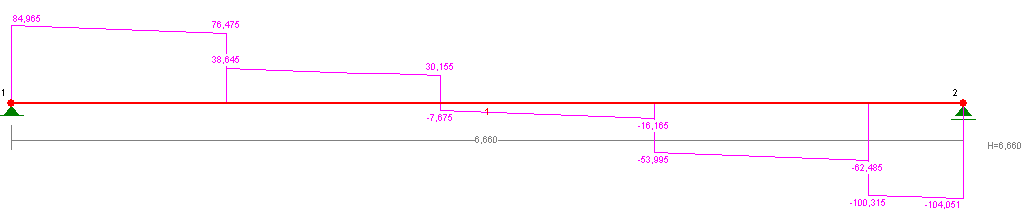
- obliczenie ugięcia belki

Budowa układu zastępczego:

ci	ξ	η
1,5	0,2252	0,6300
3	0,4505	0,9858
0,5	0,0751	0,2235
2	0,3003	0,7926
SUMA	-	2,6318

-obliczenie ugięcia rzeczywistego belki:

- wartość ugięcia dopuszczalnego

(tablica 4 normy)

Warunek SGU nie został spełniony.

Przyjmuję dwuteownik zwykły I 360 o następujących parametrach:

Wx = 1090 cm³ I_x= 19610 cm⁴ I_y=818cm⁴ g=0,77kN/m A= 97,1cm²

2.5.6. Korekta wartości obciążenia obliczeniowego oraz sił wewnętrznych.

g₀ = g₀ + (g · a) = 6,21+0,77⋅1,1= 7,06 kN/m

2.5.7. Sprawdzenie SGN (Stanu Granicznego Nośności) dla belki A-3:

- wyznaczenie klasy przekroju:

h = 360 mm

b_f = 143 mm

t_f = 19,5 mm

t_w = 13 mm

R = 13 mm

- klasa środnika (tablica 6 pozycja A normy)

Środnik jest w klasie 1.

- klasa pasów (tablica 6 pozycja b normy):

Pas znajduje się w klasie 1.

Przekrój znajduje się w klasie 1.

2.5.7.1 Sprawdzenie nośności.

Nośność obliczeniowa ścianek ścinanych określana jest wzorem 16 normy :

- współczynnik niestateczności przy ścinaniu

- pole przekroju czynnego przy ścinaniu

f_d - wytrzymałość obliczeniowa stali

Warunek nośności przekroju:

Warunek nośności został spełniony.

2.5.7.2 Sprawdzenie nośności na momenty.

Nośność obliczeniową przekroju wyznaczam ze wzoru 42 normy:

M_R=

Warunek nośności przekroju zabezpieczenia przed zwichrzeniem:

Warunek nośności został spełniony.

2.5.8 Sprawdzenie SGU (Stanu Granicznego Użytkowania):

-obliczenie ugięcia rzeczywistego belki:

- wartość ugięcia dopuszczalnego

(tablica 4 normy)

Ostatecznie przyjmuje belkę A-3 jako I 360 o parametrach:

W_x = 1090 cm³ I_x= 19610 cm⁴ I_y=818cm⁴ g=0,77kN/m A= 97,1cm²

W stropie ostatecznie występują belki:

A-1 : I 240;

A-2: I 240;

A-3: I 360.

2.6. Sprawdzenie muru na docisk ( wg. PN-B-3002:1999):

2.6.1. Ustalenie parametrów wytrzymałościowych dla muru:

-naprężenie pod belką A-1

Belka IPN 240 o szerokości s= 0,106m obciąża mur siłą N_id= 41,3kN. Oparcie belki:

Naprężenia działające pod belką:

-obliczenie wytrzymałości muru na ściskanie

Mur wykonany jest z cegły klasy 25 oraz na zaprawie marki 10

Współczynnik bezpieczeństwa
dla I kategorii produkcji elementów murowanych oraz kategorii B wykonania robót:

Efektywne pole przekroju ściany:

Nośność muru pod obciążeniem skupionym

Nośność muru poddanego działaniu obciążenia skupionego jest wystarczająca.

-naprężenie pod belką A-2

Belka IPN 240 o szerokości s= 0,106m obciąża mur siłą N_id= 36,46kN. Oparcie belki:

Naprężenia działające pod belką:

-obliczenie wytrzymałości muru na ściskanie

Mur wykonany jest z cegły klasy 25 oraz na zaprawie marki 10

Współczynnik bezpieczeństwa
dla I kategorii produkcji elementów murowanych oraz kategorii B wykonania robót:

Efektywne pole przekroju ściany:

Nośność muru pod obciążeniem skupionym

Nośność muru poddanego działaniu obciążenia skupionego jest wystarczająca.

-naprężenie pod belką A-3

Belka IPN 360 o szerokości s= 0,143m obciąża mur siłą N_id= 36,46kN. Oparcie belki:

Naprężenia działające pod belką:

-obliczenie wytrzymałości muru na ściskanie

Mur wykonany jest z cegły klasy 25 oraz na zaprawie marki 10

Współczynnik bezpieczeństwa
dla I kategorii produkcji elementów murowanych oraz kategorii B wykonania robót:

Efektywne pole przekroju ściany:

Nośność muru pod obciążeniem skupionym

Nośność muru poddanego działaniu obciążenia skupionego jest wystarczająca.

3. Obliczenie podciągu głównego (blachownicy) B-1

3.1 Schemat statyczny wartości sił wewnętrznych

-obciążenie blachownicy

Siły skupione:

-reakcje belki A-1:

-reakcje belki A-3B

Obciążenie rozłożona:

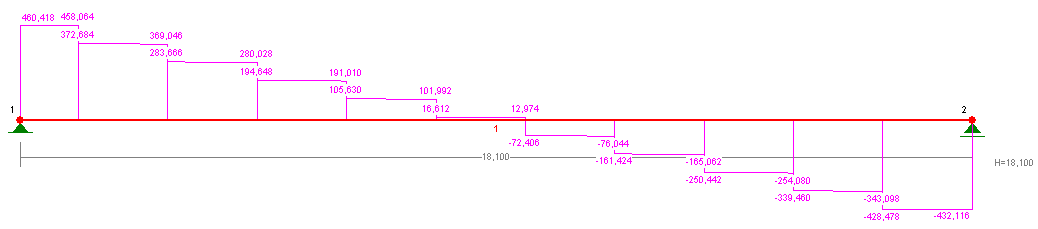
3.2. Kształtowanie poprzeczne blachownicy:

Założenia:

- blachownica zabezpieczona przed zwichrzeniem

- zakładam przekrój klasy 4;

- zakładam współczynnik niestateczności miejscowej

- obliczenie wskaźnika wytrzymałości przekroju na zginanie:

W_x
; W_x
W_x

-założenie do optymalnego kształtowania blachownicy:

• 
  
  

• 
  

• 
  

• 
  

• 
  

Ostatecznie przyjmuję wymiary przekroju poprzecznego blachownicy:

3.3 Korekta sił wewnętrznych blachownicy:

- obciążenie blachownicy:

Siły skupione:

• Reakcje belki A-1:
  

• Reakcja belki A-3:
  

Obciążenie rozłożone:

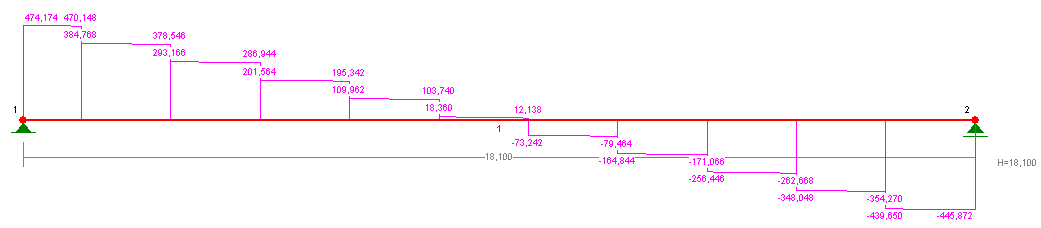
3.4 Sprawdzenie stateczności ścianek blachownicy:

3.4.1 Przekrój 1-1:

a.) sprawdzanie stateczności środnika:

• Sprawdzenie warunku nośności obliczeniowej zredukowanej M_{R­_V}:

Klasa przekroju na ścinanie (tablica 7):

Należy uwzględnić współczynnik miejscowej utraty stateczności.

- obliczenie współczynnika niestateczności miejscowej przy ścinaniu (tablica 8):

-obliczenie smukłości względem ścianki:

-współczynnik niestateczności miejscowej:

- pole czynne przy ścinaniu:

-nośność przekroju na ścinanie:

W dalszych obliczeniach nie uwzględniam nośności obliczeniowej zredukowanej

-sprawdzenie stateczności środnika:

Obliczenie wartości naprężenia na wysokości środnika pułki:

- obliczenie smukłości względnej ścianki: :

-współczynnik niestateczności miejscowej:
(tablica 9)

- nośność obliczeniowa przekroju na zginanie:

-warunek stateczności środnika:

Stateczność środnika jest zachowana.

b.) sprawdzenie stateczności pasa ściskanego

naprężenia maksymalne w włóknach skrajnych:

2.6 Sprawdzenie oparcia (docisku) belki na murze.

2.6.1 Wyznaczenie wytrzymałości obliczeniowej muru na ścinanie

*przyjęto cegłę pełną klasy 15MPa na zaprawie klasy M10

-ηw=1

-δ=0,81 dla cegły zwykłej

-fB=15MPa

-K=0,5

-fm=10Mpa

-ηA=1 dla A>30cm²

-γm=1,7 kategoria I wykonawstwa A

-Wyznaczenie wytrzymałości obliczeniowej muru na ściskanie:

-wytrzymałość na ściskanie elementu murowego

fb= ηw* δ* fB=1*0,81*15=12,15MPa

-wytrzymałość charakterystyczna muru na ściskanie:

fk=K*fb^0,65*fm^0,25=0,5*12,15^0,65*10^0,25=4,508MPa

-wytrzymałość obliczeniowa muru na ściskanie:

fd=fk/( ηA* γm)=4,508/(1*1,7)=2,65MPa

2.6.2 Sprawdzenie docisku dla belki A-1

Długość oparcia a<15cm+h/3cm=15+34/3=26,333 przyjęto a = 24cm

-Wyznaczenie naprężeń docisku:

-σd=RA-1/Ab

-pole oddziaływania obciążenia skupionego Ab

Ab=a*s=0,24*0,137=0,03288m²

-naprężenia docisku

σd =51,638/0,03288=1570,498kPa=1,57MPa

-efektywne pole przekroju ściany

Aeff=leff*t

Przyjęto: H=10m

leff=s+2*(H/2)/tg60=0,137+2*(10/2)/1,732=5,91m

a1= (leff - s)/2=(5,91-0,137)/2=2,886m

a1=5/tg60=2,886

Aeff=5,91*0,51=3,0141m

-weryfikacja warunku docisku σd

x=2*a1 /H <1,0

x=2*2,886/10=0,5772<1,0

σd=1,57 <fk/γm(1+0,15x)(1,5-1,1*Ab/Aeff)=4,508/1,7[(1+0,15*0,5772)(1,5-1,1*0,03288/3,0141)=

=4,287MPa

-weryfikacja warunku docisku σd:

σd < 1,394*fd

σd =1,57 < 1,394*2,65=3,694MPa

Wniosek:

Oparcie belki A-1 nie wymaga zastosowania podkładki.

2.6.3 Sprawdzenie docisku dla belki A-2

Długość oparcia a<15cm+h/3cm=15+30/3=25 przyjęto a = 20cm

-Wyznaczenie naprężeń docisku:

-σd=RA-2/Ab

-pole oddziaływania obciążenia skupionego Ab

Ab=a*s=0,20*0,125=0,025m²

-naprężenia docisku

σd =45,041/0,025=1801,64kPa=1,8MPa

-efektywne pole przekroju ściany

Aeff=leff*t

Przyjęto: H=10m

leff=s+2*(H/2)/tg60=0,125+2*(10/2)/1,732=5,898m

a1= (leff - s)/2=(5,898-0,125)/2=2,886m

a1=5/tg60=2,886

Aeff=5,898*0,51=3,008m

-weryfikacja warunku docisku σd

x=2*a1 /H <1,0

x=2*2,886/10=0,5772<1,0

σd=1,8 <fk/γm(1+0,15x)(1,5-1,1*Ab/Aeff)=4,508/1,7[(1+0,15*0,5772)(1,5-1,1*0,025/3,008)=

=4,295MPa

-weryfikacja warunku docisku σd:

σd < 1,394*fd

σd < 1,394*2,65=3,694MPa

Wniosek:

Oparcie belki A-1 nie wymaga zastosowania podkładki.

2.6.4 Sprawdzenie docisku dla belki A-3

Długość oparcia a<15cm+50/3cm=15+34/3=31,666cm przyjęto a =30cm

-Wyznaczenie naprężeń docisku:

-σd=RA-3/Ab

-pole oddziaływania obciążenia skupionego Ab

Ab=a*s=0,3*0,185=0,0555m²

-naprężenia docisku

σd =199,732/0,0555=3598,774kPa=3,6MPa

-efektywne pole przekroju ściany

Aeff=leff*t

Przyjęto: H=10m

leff=s+2*(H/2)/tg60=0,185+2*(10/2)/1,732=5,96m

a1= (leff - s)/2=(5,96-0,185)/2=2,8875m

a1=5/tg60=2,8867

Aeff=5,96*0,51=3,0369m

-weryfikacja warunku docisku σd

x=2*a1 /H <1,0

x=2*2,8867/10=0,5773<1,0

σd=3,6 <fk/γm(1+0,15x)(1,5-1,1*Ab/Aeff)=4,508/1,7[(1+0,15*0,5773)(1,5-1,1*0,0555/3,0369)=

=4,287MPa

-weryfikacja warunku docisku σd:

σd < 1,394*fd

σd =3,6 < 1,394*2,65=3,694MPa

Wniosek:

Oparcie belki A-1 nie wymaga zastosowania podkładki.

3.0 Obliczenie podciągu głównego B

3.1 Schemat statyczny:

g*=(70+10*l0)*0,85=(70+10*17,99)*0,85=212,515kG/m=2,125kN/m

Wartości obciążenia siłami skupionymi:

-wartości obliczeniowe

RA-1=51,638kN RA-3 =199,732kN

2* RA-1=103,276kN 2* RA-3 =399,464kN

-wartości charakterystyczne

RA-1= 41,527kN RA-3 =158,451kN

2* RA-1=83,054kN 2* RA-3 =316,9kN

Mmax=3586,042kNm

Vmax=749,838 1

3.2 Wstępny dobór przekroju blachownicy:

Mr=αp*Wx*fd

Przyjęto stal St3SY 16mm<t<40mm→ fd=205MPa

Założono klasę przekroju 1,2 → przyjęto αp = 1 dla belek wolnopodpartych

φL=1 - usztywnienie pasa górnego belkami A-1

M'max/(Wx* fd)=1 → Wx= M'max/ fd

Wx= 3586,042/205000=0,017493 m³=17493 cm³

Zwiększono sprężysty wskaźnik zginania o około 20%:

Przyjęto wymiary:

Ix=tw*hw³/12+2*(bf*tf³/12+ tf * bf(hw/2+tf/2)²

y=hw/2+tf

Wx=Ix/y

-optymalizacja wymiarów blachownicy:

-hw/l=(1/10-1/15) → hw/17990=1/13→ hw ~ 1400mm

-tw=7+3* hw=7+3*1,4=11,2mm

- tf=28-32mm → przyjęto tf ~ 30mm

-b/ tf<25 → b<750mm

→przyjęto wymiary:

tf=30mm

b=420mm

hw=1400mm

tw=12mm

A=2*(b* tf)+( tw* hw)=2*(42*3)+(1,2*140)=420cm²

Ix=tw*hw³/12+2*(bf*tf³/12+ tf *bf(hw/2+tf/2)²=1,2*140³/12+2*(42*3³/12+3*42(140/2+3/2)² =1562882cm^4

y=hw/2+tf=140/2+3=73cm

Wx=Ix/y=1562882/73=21409cm³

Q=7,85*420=3297=3,3kN/m

3.3 Zestawienie obciążeń

-wartości obliczeniowe

g0=3,3*1,1=3,63kN/m

-wartości charakterystyczne

gk=3,3kN/m

3.4 Obliczenia sił wewnętrznych i kształtowanie podłużne blachownicy.

-max momenty zginające i siły tnące na granicach przedziałów

Mmax I =3613,311kNm

V max I=-2,598kNm

Mmax II =3065,837kNm

V max II=322,113kN

Mmax III =1947,556kNm

V max III=538,103kN

Ra=755,182

Rb=1155,450

-charakterystyki poszczególnych odcinków

WxI=21409cm³

WxII=Mmax II /fd=3065,837/205000=14955,302 cm³

WxIII=Mmax III /fd=1947,556/215000=90584 cm³

-przyjęto

I: tfI=30mm→ IxI=1562882cm^4→ WxI=21409 cm³

II: tfII=25mm→ IxII=1340587,5 cm^4→ WxII=18490 cm³

III: tfIII=16mm → IxII1= 947176,272cm^4→ WxIII=13247cm³

3.5 Sprawdzenie nośności blachownicy - weryfikacje SGN

-wyznaczenie klasy przekroju

ε= √(215/205)=1,025

-dla środnika

b/t=hw/tw=1400/12=116,666>105 ε → klasa 4

-dla półek

b/t=(s/2-tw/2)/hf=(420/2-12/2)/16=12,75<14ε → klasa 4

Wniosek: Cały przekrój należy do klasy 4.

-wyznaczenie Ψ dla stanu krytycznego:

β=a/b=1200/1400=0,857<1 ν=0

K2=0,4/(1- ν)=0,4

λp=(b/t)*(K/56)* √(fd/215)

λp=1400/12*0,4/56*√(215/215)=0,8333 → φp= Ψ =0,934

-warunek nośności elementu jednokierunkowo zginanego:

Mmax/(φL*MR)<1

- nośność przekroju przy jednokierunkowym zginaniu dla klasy 4

MRI= Ψ* WxI*fd=0,934*21409*10^-6*205000=4099,2kNm

MRII= Ψ* WxII*fd=0,934*18490,9*10^-6*205000=3540,4kNm

MRII= Ψ* WxIII*fd=0,934*13247,2*10^-6*215000=2660,2kNm

-weryfikacja warunku:

I: MmaxI/(φL*MRI)=3613,3/(1,0*4099,2)=0,88<1

II: MmaxII/(φL*MRII)=3065,8/(1,0*3540,45)=0,87<1

III: MmaxIII/(φL*MRIII)=1947,556*/(1,0*2660,2)=0,73<1=

WNIOSEK: Warunek SGN ze względu na zginanie został spełniony w każdym przekroju.

-warunek nośności elementu ścinanego

ε= √(215/fd)= √(215/205)=1,025

-warunek smukłości

hw/tw=1400/12=116,666>105* ε

-pole czynne przy ścinaniu

Av=hw* tw=1400*12=1,68*10^-2m²

-współczynnik niestateczności przy ścinaniu

φpv=1/λp=1/0,883=1,2>1 przyjęto φpv=1

-nośność przekroju przy ścinaniu

VR=0,58* φpv* Av *fd=0,58*1*1,68*10^-2*205000=1997,52kN

-weryfikacja warunku

Vmax/VR =755,986/1997,52=0,378<1

-sprawdzenie warunku przy zredukowaniu nośności na ścinanie:

V0=0,3* VR=0,3*1997,52=599,256kN

Ponieważ VI,VII,VIII<0,3 VR nie zachodzi konieczność redukcji nośności przekroju na zginanie do wartości MR,V.

WNIOSEK:

Warunek stanu granicznego ze względu na ścinanie został spełniony w każdym przekroju.

3.6 Weryfikacja stateczności ścianek blachownicy.

Warunek stateczności σc/( φp*fd)<1

-środnk

φp = 0,934

fd=215MPa - tw<16mm

σ= MmaxI/Wx1=3613,311/21409*10^-6=168775kPa=169,4 MPa

σc= σ*hw/h=168,7*1400/1460=161,76MPa

-weryfikacja warunku:

σc/( φp*fd)=161,76/(0,934*215)=0,8<1

WNIOSEK: Warunek stateczności dla środnika został spełniony.

- pas sciskany

fd=205 MPa - dla 16mm<tf<40mm

φp=f(λp)

λp=(b/t)*(K/56)* √(fd/215)

b1=0,5b-0,5tw=0,5*420-0,5*12=204mm ; t=tf=30mm

β=a/b a=1200mm , b = b1=204 → β=1200/204=5,88>1,6 ; ν=(2σ*0,5)/σ=1

K=2,2*0,8*ν=2,2+0,8*1,0=3,0

λp=204/30*3/56*√(205/215)=0,355→ φp= Ψ =1

-weryfikacja warunku

σc/( φp*fd)=161,76/(1,0+205)=0,789<1

WNIOSEK:

Warunek stateczności dla pasa ściskanego został spełniony.

3.7 Wymiarowanie żeber poprzecznych.

3.7.1. Dobór wymiarów:

-Przyjęto:tz=13mm ε=√(215/fd)

Przyjęto stal St3SY → fd=215MPa → ε=1→ bz/tz<14 ε →bz<14*tz=182mm

Przyjęto bz=180mm

-szerokość współpracująca środnika: 30tw=360mm

Rozmieszczenie żeber:

Przyjęto rozmieszczenie żeber w odległości a=1200mm pod belkami A-1 oraz pod podporami. Rozstaw żeber poprzecznych powinien spełniać warunek:a<2hw

A=1200mm<2hw=2*1400mm=2800mm - warunek spełniony

-Warunek sztywności:

Is>k*bz*tz³

Is= moment bezwładności przekroju żebra obustronnego razem z częściąwspółpracującą względem osi środnika

Is= Ix=30*tw³/12+2*(tz*bz³/12+ bz* tz(bz/2+ tw/2)²) =360*12³/12+2*(13*180³/12+180*13*(90+6)²) =51840+55766880=5582cm^4

k=1,5*(b/a)²=>0,75 , gdzie b=hw, a-odległość między żebrami

k=1,5*(1400/1200)²=1,75>0,75

-weryfikacja warunku

Is=5582cm^4>1,75*18,0*1,3³=69,2055cm^4

Wniosek:

Żebro poprzeczne o przyjętych wymiarach spełnia warunek sztywności.

3.7.2 Weryfikacja warunków nośności żebra.

-Sprawdzenie nośności żebra pośredniego na ściskanie:

Warunek nośności dla elementów ściskanych osiowo:

N/(φ*NRC)<1 gdzie N=2*RA-1=2*51,638=103,276kN

-nośność obliczeniowa przekroju przy osiowym sciskaniu

NRC=Ψ*A*fd

Wyznaczenie klasy przekroju:

ε=√(215/fd)= √(215/215)=1

-dla żebra przyjęto wymiary zakładając klasę żebra nie większą niż 3

bz/tz=180/13=13,84<14 ε →klasa3

Dla przekroju klasy 3 Ψ=1

A=2*bz*tz+30tw* tw=2*180*13+30*12*12=9*10^-3m²

NRC=1*9*10^-3*215000=1935kN

-Współczynnik wyboczeniowy φ

φ= f(λ,ao)

λ= λ/ λp λ=μ*l0/ix

μ=0,8 dla żeber pośrednich i podporowych

l0= hw=1400mm

ix=√(Ix/A)= √(5582/(2*1,3*18+30*1,2*1,2))=62,02cm

λ=0,8*1400/62,02=18,6

λp=84*√(215/fd)=84

λ=18,6/84=0,221 → φ=0,977

-weryfikacja warunku

N/(φ*NRC)=103,276/(0,977*1754,4)=0,06<1

Wniosek: Warunek nośności żebra podłużnego został spełniony.

-Sprawdzenie nośności żebra podporowego na ściskanie:

Warunek nośności dla elementów ściskanych osiowo:

N/(φ*NRC)<1

N=Rb=1155,450kN

φ=0,9635

NRC=1754,4kN

-weryfikacja warunku

N/(φ*NRC)=1155,450/(0,9635*1754,4kN)=0,683<1

WNIOSEK: Warunek nośności żebra podporowego został spełniony.

-sprawdzenie nośności żebra pośredniego na docisk:

Warunek docisku:

σd=N/Ad<fdb

N=2*RA-1=2*51,638=103,276kN

fdb= wytrzymałość na docisk powierzchni płaskiej do powierzchni płaskiej

fdb=1,25fd=1,25*215=268,75MPa

Ad=2*(bz-c)*tz ; przyjęto wycięcie w żebrze na spiony c=30mm

Ad=2*(bz-c)*tz=2*(180-30)*13=3120mm²=3,9*10^-3m²

-weryfikacja warunku

N/Ad=103,276/3,9*10^-3=26481kPa=26,481MPa< fdb=268,75MPa

WNIOSEK: Warunek nośności żebra pośredniego na docisk został spełniony

Warunek nośności żebra pośredniego na docisk został spełniony.

-Sprawdzenie nośności żebra podporowego na docisk

Warunek docisku:

kN

MPa

mm² =
m²

- weryfikacja warunku

kPa =296,7 MPa >
MPa

Warunek nośności żebra podporowego na docisk nie został spełniony.

Wyliczenie potrzebnej grubości żebra podporowego

m = 15,00 mm

Przyjęto grubość żeber podporowych
mm

3.7.3. Dobór grubości spoiny połączenia żeber z blachownicą:

-Warunek nośności połączenia zakładowego przy obciążeniu osiowym:

τ = RA-1/∑li*a<αfd

RA-1=51,638kN

∑li=2*(hw-2c)=2*(1400-2*30)=2740mm

α=0,8 Re<255 fd=215MPa

-wyznaczenie obliczeniowej grubości spoiny:

τ = RA-1/∑li*a<αfd →a>F/ αfd∑li

a>51,638/(0,8*215000*2,74)=0,000109m=0,109mm

-wyznaczenie grubości spoiny z warunków konstrukcyjnych

0,2t2<10mm<anom<0,7t1

2,6< anom<8,4mm

2,5mm< anom<16mm

t1=12

t2=13

t1< t2

Przyjęto grubość spoiny a=3mm

-weryfikacja warunku nośności połączenia żebra ze środnikiem:

τ = 51,638/2,74*0,0026=7,25MPa<0,8*215=172MPa

WNIOSEK: Warunek nośności połączenia żebra ze środnikiem został spełniony.

3.8 Dobór grubości spoiny połączenia środnika z pasami blachownicy.

-Warunek nośności połączenia pasa ześrodnikiem:

τ=Q*Sx/∑a*Ix

Weryfikacja spoiny nad podporą:

Q=Qmax=Rb=1155,450kN

Sx=tf*bf*(0,5*hw+0,5*tf)=0,016*0,42*(0,5*1,4+0,5*0,0016)=4,7*10^-3m³

Ix=947176,272cm^4=9,47*10^-3m^4

∑a=2a

α= 0,8 Re<255MPa fd=215MPa

-wyznaczenie obliczeniowej grubości spoiny:

τ=Q*Sx/∑a*Ix< α* fd →a> Q*Sx/ Ix* α* fd*2

a>1155,450*4,7*10^-3/(2*215000*0,8*9,47*10^-3)=0,001667m

Przyjęto a=1,7mm

-wyznaczenie grubości spoiny z warunków konstrukcyjnych:

0,2t2<10mm<anom<0,7t1

2,5mm< anom<16mm

t1=12

t2=30,25,16

0,2*30=6<10mm<anom<0,7*12=8,4

0,2*25=5<10mm<anom<0,7*12=8,4

0,2*16=3,2<10mm<anom<0,7*12=8,4

2,5mm< anom<16mm

Przyjęto grubośc spoiny a = 6mm

-weryfikacja warunku nośności połączenia żebra ze środnikiem:

τ = 1155,450*4,7*10^-3/(2*0,006*9,47*10^-3)=47,787MPa<0,8*215=172MPa

WNIOSEK: Warunek nośności połączenia żebra ze środnikiem został spełniony.

3.9Wymiarowanie styku montażowego blachownicy.

Blachownice podzielono na 3 części.

MII=3065,837 kNm WII=18490cm³

-wyznaczenia styku czołowego w pasie dolnym blachownicy:

σ=M/Wx<αfd α=1-0,15ν=1-0,15*1=0,85

σ= M/Wx=3065,837/1,85*10^-2=165,72MPa<αfd=0,85*205=174,3MPa

WNIOSEK: Ze względów konstrukcyjnych zdecydowano się na zastosowanie styku zamkowego. Spoiny dolne przesunięto o 400mm w kierunku podpór

3.10 Sprawdzenie ugięcia blachownicy - weryfikacja stanu granicznego użytkowania>

Warunek fgr>frz

-ugięcie dopuszczalne

fgr=l/350=17,99/350=0,0514m

-ugięcie rzeczywiste

frz=qkc/(24*E*Ix1)*(5/16l^4+α1*x10^3*(4l-3* x10)+ α2*x20^3*(4l-3* x20))

Dane:

X10=2,9

X10=5,5

l=17,99

IxI=1562882cm^4

IxII=1340587,5 cm^4

IxII1= 947176,272cm^4

qkc=qk+∑2*RA-1/l RA-1-reakcja na belce A-1 z obciążenia charakterystycznego RA-1=41,527

qkc=3,3+14*2*41,527/17,99=67,93kN/m

α1=IxI/IxII-1=1562882/1340587,5-1=0,166

α2= IxI/IxIII- IxI/IxII=1562882/947176,272-1562882/1340587,5=0,484

frz=67,93/(24*205*10^6*1,563*10^-2)*(5/16*17,99^4+0,166*2,9^3*(4l-3* 2,9)+ 0,484*5,5^3*(4*17,99-3* 5,5))=8,83*10^-7*(32732,16+256.11+4465,944))=0,033

frz=0,033m< fgr= 0,0514m

WNIOSEK: Warunek stanu granicznego użytkowalności został spełniony.

3.11 Wymiarowanie łożyska podporowego blachownicy.

-przyjęcie wymiarów poziomych:

b=bf=2*0,05+0,42=0,52m → przyjęto b=0,55m

d=1/3a

σd=RB/a*b → σd=8MPa dla B15→ a= RB/ σd*b→a=755,182/(8000*0,55)=0,17m→ przyjęto a=0,20

σd=RB/a*b=755,182/0,55*0,20=6,865MPa<8MPa

d=1/3a=20/3≈7cm

-przyjęcie grubości blachy podłożyskowej:

Moment zginający blachę podłożyskową:

Mα= σd*b*0,5c²=6865*0,55*0,5*((0,20-0,07)/2)²=7,976kNm

Grubosć blachy:

tpł=√((6 Mα)/(b*fd)= √((6 *7,976)/(0,55*205000)=0,02m=20mm>tmin=8mm

→ przyjęto blachę podłożyskową 200*550*20mm

-Wymiarowanie łożyska:

-Wyznaczenia grubości łożyska

Mβ= σd*b*0,125*a²=6865*0,55*0,125*(0,20)²=18,878kNm

W=Wpł+Wł → Wł=W- Wpł

Wpł=b*tp/6=0,55*0,02²/6=3,666*10^-5m³

W= Mβ/fd=18,878/205000=0,92*10^-4m³

Wł→b*tł²/6 → tł=√(( W- Wpł)*6/b) → tł=√((0,92*10^-4-3,666*10^-5)*6/0,55=0,0246m

Przyjęto tł=0,025m

-obliczenie promienia łożyska:

σbH=0,42*√(p*E/r)<fdbH=3,6fd

r>p*E/(3,6fd/0,42)²)

p=RB/b=755,182/0,55=1373,06kN/m

r>1373,06*205*10^6/(3,6*205000/0,42)²=0,09m<rmin=0,5m

→Przyjęto łożysko podporowe: 70*550*25mm o promieniu r=500mm

-Sprawdzenie docisku łożyska do blachy podłożyskowej:

σd=RB/b*d=755,182/0,55*0,07=19,615<1,25*205=256MPa

WNIOSEK: Wytrzymałość blachy podłożyskowej na docisk jest wystarczająca.

4.0 Wymiarowanie połączeń belek stalowych

4.1 Obliczenie połączenia belki A-2 z podciągiem A-3.

Przyjęto łączenie śrubami M16 klasy 4.8.

g=10,8 mm.

-Rozmieszczenie śrub w połączeniu

(24 mm ; min(129,6 mm, 150 mm, 83,2 mm))

mm
przyjęto
mm

mm))

(40 mm; min(151,2 ; 200 mm))
przyjęto a = 80 mm

łącznie szerokość blachy b = 2
+2a = 2*40+2*80 = 240 mm

mm

-Obciążenie skrajnych śrub

kNm

kN

kN

wypadkowa:
kN

-Nośność śruby na ścięcie trzpienia

Mpa m = 1

m²

kN

-Nośność na docisk trzpienia do ścianki otworu

lub

przyjęto

Mpa
mm

kN

-Weryfikacja warunku nośności śruby

kN
kN}

Warunek jest spełniony.

-Sprawdzenie warunku nośności połączeń obciążonych siłą poprzeczną.

kN

mm² =
m²

mm² =
m²

kN

kN

Nośność połączenia na siłę poprzeczną jest wystarczająca.

4.2. Obliczenie połączenia belki A-1 z blachownicą.

Do wymiarowania przyjęto śruby M16 klasy 4,8.

Połączono za pomocą żeber pośrednich g = 13 mm

-Rozmieszczenie śrub w połączeniu

(24 mm ; min(156 mm, 150 mm, 92 mm))

mm
przyjęto
mm
mm

mm))

(40 mm; min(182, 200 mm))
przyjęto a = 80 mm

łącznie szerokość blachy b = 280 mm

mm

-Obciążenie skrajnych śrub

kNm

kN

kN

wypadkowa:
kN

-Nośność śruby na ścięcie trzpienia

Mpa m = 1

m²

kN

-Nośność na docisk trzpienia do ścianki otworu

lub

przyjęto

Mpa
mm

kN

-Weryfikacja warunku nośności blachy

kN
kN}

Warunek jest spełniony.

-Sprawdzenie warunku nośności połączeń obciążonych siłą poprzeczną.

kN

mm² =
m²

mm² =
m²

kN

kN

Nośność połączenia na siłę poprzeczną jest wystarczająca.

4.3. Obliczenie połączenia podciągu A-3 z blachownicą

Przyjęto łączenie śrubami M16 klasy 4.8.

Połączono za pomocą żebra podporowego g = 15 mm

• Rozmieszczenie śrub w połączeniu

(24 mm ; min(180 mm, 150 mm, 100 mm))

mm
przyjęto
mm
mm

mm))

(40 mm; min(210, 200 mm))
przyjęto a = 100 mm

łącznie szerokość blachy b = 350 mm

mm

-Obciążenie skrajnych śrub

kNm

kN

kN

wypadkowa:
kN

-Nośność śruby na ścięcie trzpienia

Mpa m = 1

m²

kN
Nośność z warunku zerwania trzpienia nie jest spełniona, przyjęto śruby M24 klasy 4.6

MPa
m²

kN

-Nośność na docisk trzpienia do ścianki otworu

lub

przyjęto

Mpa
mm

kN

-Weryfikacja warunku nośności blachy

kN
kN}

Warunek jest spełniony.

-Sprawdzenie warunku nośności połączeń obciążonych siłą poprzeczną.

kN

mm² =
m²

mm² =
m²

kN

kN

Nośność połączenia na siłę poprzeczną jest wystarczająca.

Ćwiczenie 2 - Słup dwugałęziowy

1.Obliczenie trzonu słupa

1.1 Wstępny dobór przekroju słupa

N=RB=1155,45kN

-Nośność obliczeniowa przekroju przy osiowym ściskaniu:

NRC=Ψ*A*fd

Założono wstępnie klasę przekroju 1.

Ψ=1 - współczynnik redukcyjny nośności obliczeniowej dla klasy 1,2,3

fd= 215MPa - dla stali St3SY o t<16

-Nośność elementów ściskanych osiowo:

N/φNRC<1

-Współczynnik wyboczeniowy φ=f(λ,c)

λ= λ/ λp

Założono wstępnie λ=100

λp=84√215/fd=84

λ=100/84=1,19 →odczytano z tabl. 11 normy z krzywej b φ=0,532

-Wyznaczenie przekroju poprzecznego z warunków na nośność elementów ściskanych osiowo:

N/(φ*Ψ*A*fd)<1 →A>N/φ*fd

A>1155,45/0,532*215000=0,0101m^2=101cm^2

→Przyjęto wstępnie 2 C280:

A1=53,3

A=2* A1=106,6cm^2

Ix1=6280cm^4

Iy1=399cm^4

ix=10,9cm

iy= 2,74

ei=2,53

-Wyznaczenie rozstawu gałęzi słupa:

Założenie: 1,1 Ix=Iy

Ix=2Ix1

Iy=2Iy1+2A1*(e/2)²

e=2√(1,1Ix1-Iy1)/A1)=2√(1,1*6280-399)/53,3)=22,1

→Przyjęto e=23cm

1.2 Wyznaczenie smukłości słupa

Dla całego przekroju:

A=106,6cm²

Ix=12560cm^4

Iy=14895,85cm^4

ix=√Ix/A=10,9cm

iy=√Iy/A=11,8cm

lx=H-0,5hA-3=7,60-0,5*0,5=7,35m

ly=H-hb=7,6-(1,4+0,03+0,016)=6,154m

-smukłość wyboczenia giętnego całego przekroju względem osi x-x:

λx=lx*μx/ix=7,35*1/0,109=67,43

-smukłość wyboczenia giętnego całego przekroju względem osi y-y:

λy=ly*μy/iy=6,154*1/0,118=52,15

-smukłośćwyboczeniowa postaciowego pojedynczej gałęzi przekroju między przewiązkami

λv=λ1=l1*μy/iy1- dla słupa usztywnionegoprzewiązkami

l1= λ1* iy1/μy ; μy=1

λ1<[0,8λx=53,94;60] → przyjęto λ1=53,94

l1=53,94*0,0274=1,478m

λv=1,487*1/0,0274=54,27

-smukłośćzastępcza elementu wielogałęziowego

λm=√( λy²+m/2* λv²)

m=2 - liczba gałęzi w płaszczyźnie przewiązek, równoległej do kierunku wyboczenia

λm=√ (52,15²+2/2*54,27²)=75,26

1.3 Obliczenie nośności trzonu słupa

Ponieważ: λm=75,26> λx=67,43> λy= 52,15 , to taki przekrój liczymy jako klasę 4 gdzie,

Ψ=min(φ1,φp)

- φ1- współczynnik wyboczeniowy ustalony dla pojedynczej gałęzi φ1=f(λv,c)

λv = λv/ λp

λp=84√215/fd=84

λv=54,27/84=0,646 →odczytano z tabl. 11 normy φ1=0,776

- φp- współczynnik niestateczności miejscowej φp=f(λp)

λp = b/t*K/56*√215/fd

b=h-2*t-2*r=280-2*15-2*15=220mm

t=g=10

K- współczynnik podparcia i obciążenia ścianki wyznaczony na podstawie tab. 8 normy

β=a/b a=l1=1478mm b=220 → β=1478/220=6,72>1 ; ν=1

K2=0,4+0,6 ν=1

λp =220/10*1/56*√(215/215)=0,393→ odczytano z tab.9 φp=1

-Wartość współczynnika redukcyjnego nośności obliczeniowej przekroju trzonu słupa:

Ψ=min(0,776;1)=0,776

-Współczynnik wyboczeniowy φ dla elementu wielogałęziowego:

φ = f(λm,b)

λm= λm/ λp*√ Ψ - dla klasy 4

λp=84√215/fd=84

λm=75,26/84*√0,776=0,79 →odczytano z tab. 11 normy φ=0,786

-weryfikacja warunku nośności elementu ściskanego osiowo:

N/φNRC<1

-nośność przekroju przy jednoosiowym ściskaniu dla klasy 4:

NRC= Ψ*A*fd=0,776*0,01066*215000=1778,5144kN

-weryfikacja warunku

N/φNRC=1155,45/(0,786*1778,5144)=0,826

WNIOSEK: Warunek stanu granicznego nośności został spełniony

1.4 Obliczenie przewiązek:

Wyznaczenie obciążenia przypadającego na przewiązkę:

Q=0,012*A*fd=0,012*0,01066*215000=27,5kN

-wartość siły poprzecznej i momentu w przewiązce:

VQ=Q*l1/(n(m-1)e)=27,5*1,478/(2*(2-1)*0,23=88,36kN

MQ= Q*l1/(n*m)=27,5*1,478/(2*2)=10,16kNm

-Przyjęcie wymiarów przewiązki:

Przyjęto przewiązkę grubości tp=12mm, szerokości bp=180mm

bp/tp=15<16ε →klasa 1

-warunek nośności elementu ściskanego:

VMax/VR<1

-nośność przekroju na ściskanie:

VR =0,58*Av*fd

Av=0,9* bp*tp=0,9*180*12=1944mm²=1,944*10^-3m²

VR =0,58* 1,944*10^-3*215000=242,41kN

-weryfikacja warunku:

przy jednokierunkowym zginaniu:

MR=Ψ*Wx*fd

Ψ=1 dla klasy przekroju 1,2,3

MR=1*0,012*0,18²/6*215000=13,93kNm

-weryfikacja warunku:

MQ/ MR,V=10,16/(0,903*13.93)=0,8

WNIOSEK: Warunek stanu granicznego nośności ze względu na zginanie został spełniony.

1.5 Obliczenie spoiny łączącej przewiązkę z gałęziami

0,2t2<10mm<anom<0,7t1

2,5mm< anom<16mm

t1=tp=12mm

t2=15mm

0,2*15=3mm< anom<0,7*12=8,4mm

2,5mm< anom<16mm

Przyjęto grubosć spoiny: a=4mm

c>{40mm;10a=40mm}, przyjęto c= s-e1=95-25,3=68mm

-Sprowadzenie obciążenia do środka ciężkości spoiny:

-środek ciężkości spoiny:

Sy1=a*b*a/2+2*a*c*c/2=4*180*4/2+2*4*68*68/2=19936mm²

x0= Sy1/A= Sy1/(a*b+2*a*c)= 19936/(180*4+2*4*68)=15,77mm

cx= x0-a=15,77-4=11,77mm

-długość przewiązki:

lp=e=230mm

-wartość momentów w środku ciężkości spoiny:

e2= lp-2 cx=230-2*11,77=206,46mm

MQ=VQ* e2/2=88,36*0,20646/2=9,12kNm

-Wyznaczenie naprężeń w spoinie:

-wyznaczenie momentów bezwładności spoin:

Ix=ab³/12+2*(c*a³/12+a*c*(b/2+a/2)²=4*180³/12+2*(68*4³/12+4*68*(180/2+4/2)²)=

Ix=654,9cm^4

Iy=b*a³/12+b*a*( cx*a/2)²+2*(a*c³/12+a*c*(c/2- cx)²)=180*4³/12+180*4*(11,77+4/2)²+2* (4*68³/12+4*68*(68/2-11,77)²)=

Iy=61,5932cm^4

I0= Ix+ Iy=654,9cm^4+61,5932cm^4=716,5cm^4

-wyznaczenie maksymalnego promienia wodzącego dla najbardziej wytężonego punktu spoiny:

r=√((b/2)²+(c-cx)²)= √((180/2+4) ²+(68-11,77) ²)=109,53mm

-naprężenia w punkcie najbardziej wytężonym:

a*∑l=4*(2*68+180)=1264mm²

τF=VQ/ a*∑l=88,36/1,264*10^-3=69905kPa

τM=MQ*r/I0=9,12*0,10953/7,165*10^-6=139415,7153kPa

cosΘ=0,51339

sin Θ=0,85815

-weryfukacja nośności spiony:

τ= √(( τM+ τF* cosΘ)²+( τF* sin Θ)²<α┴fd

τ=√((139415,7153+69905*0,51339)²+( 69905*0,85815)²)=168190,9< α┴fd=0,9*215000 =193000kPa

WNIOSEK: Nośność spoiny jest wystarczająca.

1.6 Zaprojektowanie przepony w trzonie słupa.

H=ly=6,154m

Przyjęto jedną przeponę umieszczoną w środku wysokości słupa.

-wyznaczenie grubości przepony

h/t<70√215/f d= 70 →t>h/70

h=hC280=280mm

t>280/70=4mm

→Przyjęto grubość przepony jako t=tmin=12mm

2.0 Obliczanie przegubowej podstawy słupa

2.1 Obliczanie blachy podstawy.

-Określenie wymiarów poziomych blachy podstawy:

N/L*B<0,8fcd

Przyjęto L ~ B →B>√(N/0,8 fcd)

fcd<13,3MPa dla B25

N=RB+Q*1,2; Q=ly*A*78,5*1,1=6,154*106,6*10^-4*78,5*1,1=5,66kN

N=1155,450+5,66*1,2=1162,242kN

B>√(1162,242/0,8*13300)=0,33m

Przyjęto wstępnie B=0,4m ; L=0,5m

-Określenie grubości blachy podstawy:

Grubość blachy podstawy określa się na podstawie wzorów Galerkina

-ekstremalny moment w strefie (1)

σd= N/B*L=1162,242/0,4*0,5=5811,21kPa

y1=(L-hC280-2*bt)/2=(0,5-0,28-2*0,014)/2=0,096m

M1= σd*y1²*0,5=5811,21*(0,096)²*0,5=26,77kNm/m

-ekstremalny moment w strefie (2)

b2=hc280=280mm

a2=(B-(e+2e1))/2=(0,4-(0,23+2*0,0253))/2=0,0597m

M2=β*σd*b2²*1

β =f(a2,b2) a2/b2=0,06/0,28=0,214 → 0,04

M2=β*σd*b2²*1=0,04*5811,21*0,28²*1=18,223kNm/m

-ekstremalny moment w strefie (3)

a3=e+2e1-2gC280=0,23+2*0,0253-2*0,01=0,26m

M3=α* σd* a3²*1

α=f(b2,a3) b2\a3=0,28/0,26=1,077 → 0,052

M3=0,052*5811,21*0,26²*1=20,427kNm/m

-wyznaczenie grubości blachy podstawy:

MMAX=[M1, M2, M3]= M1=26,77kNm/m

tp>√(6*MMax/fd)= √(6*26,77/205000)=0,028m

→przyjęto blachę podstawy: 400*500*30mm

2.2 Obliczenie blachy trapezowej

2.2.1 Określenie wymiarów blachy trapezowej.

Wyznaczenie wysokości blachy trapezowej z warunków konstrukcyjnych

0,2t2<10mm<anom<0,7t1

2,5mm< anom<16mm

t1=10mm

t2=14mm

0,2*14=2,8mm< anom<0,7*10=7mm

2,5mm< anom<16mm

-przyjęto grubość spoiny: a=5mm

-wysokość blachy trapezowej

τ=N/a*∑l ∑l=4ht

α║=0,8 fd=215MPa

τ=N/a*4ht< α║*fd → ht>N/(a*4* α║*fd)

ht>1162,242/(0,005*4*0,8*215000)=0,34m

Przyjęto wysokość blachy trapezowej ht=0,35m

-Wyznaczenie szerokości blachy trapezowej z warunku docisku:

σd=0,5N/Ad<fdb=1,25fd

0,5N=0,5*1162,242=581,121kN

Ad=bt*lt=0,014lt

0,5N/0,015lt<1,25fd → lt>0,5N/0,014*1,25fd

lt>581,121/(0,014*1,25*215000)=154mm>B

Przyjęto blachę trapezową: 400*350*14mm

2.2.2 Sprawdzenie przekroju blachy trapezowej.

-środek ciężkości na osi m-m

Sx1=2*bt*ht²+tp*L*(tp/2+ht)=2*0,14*0,35²/2+0,03*0,05*(0,03/2+0,35)=7,19*10^-3m³

A=2* ht*bt+tp*L=2*0,35*0,014*0,5*0,03=0,0248m²

cy= Sx1/A=7,19*10^-3/0,0248=0,29m

-Siły wewnętrzne:

Vα= σd*L*a2=5811,21*0,5*0,0597=173,464kN

Mα= Vα*0,5*a2=173,464*0,5*0,0597=5,1778kNm

-Obliczenie nośności przekroju:

VR=0,58*AV*fd

AV=2*ht*bt=2*0,35*0,014=0,0098m²

VR=0,58*0,0098*215000=1222,1kN

V0=0,3*VR=366,6kN

Ponieważ Vα< V0 nie zachodzi konieczność redukci obciążenia nośności przekroju na zginanie do wartości MR,V.

MR=αp*Wm*fd=

Im=2*( bt*ht³/12+ bt*ht*(ht/2-cy)²+L*tp³/12+L*tp*(ht+tp/12-cy)²=

2*(1,4*35³/12+1,4*35*(35/2-29)²)+50*3³/12+50*3*(35+3/2-29)²)=31515cm^4

Wm=Im/cy=31515/29=1087cm³

MR=1*1087*10^-6*215000=233,7kN

-Weryfikacja warunków nośności przekroju blachy trapezowej:

Mα/MR<1, Vα<VR<1

Mα/MR=5,1778/233,7=0,022<1

Vα<VR=173,464/1222,1=0,142<1

WNIOSEK: Nośność przekroju blachy trapezowej na ścinanie i zginanie jest wystarczająca.

2.3 Obliczanie spoin w podstawie słupa.

2.3.2 Spiony pionowe.

Jak w punkcie 2.2.1

2.3.2 Spoiny poziome.

-wyznaczenie grubości spoiny z warunków konstrukcyjnych

0,2t2<10mm<anom<0,7t1

2,5mm< anom<16mm

t1=14mm

t2=30mm

0,2*30=6mm< anom<0,7*14=9,8mm

2,5mm< anom<16mm

-Przyjęto grubość spoiny a=7mm

-Wyznaczenie naprężeń stycznych prostopadłych spoiny:

τ┴=N/a*∑l<α┴*fd

∑l=2*B+4*a2=2*0,4+4*0,0597=1,0388m

τ┴=1162,242/(0,007*1,0388)=159833kPa< α┴*fd=0,9*205000=184500kPa

-Wyznaczenie naprężeń stycznych równoległych spoiny:

τ║=Vα*Sm/Im*∑a< α║*fd

∑a=4a=4*0,007=0,028m

Vα=173,464kN

Im=31515cm^4

Z=29cm

Sm=L*tp*(ht+tp/2-z)=50*3*(35+3/2-29)=1125cm³

τ║=173,464*1125*10^-6/(31515*10^-8*0,028)= 22115kPa<α║*fd=0,8*205000=164000kPa

-weryfikacja warunku nośności spoiny pachwinowej:

χ√(3*( τ║²+ τ┴²))<fd

0,7*√3(22115²+159833²))=195633kPa<fd=205000kPa

2.4 Zakotwienie płyty poziomej z fundamentem.

Przyjęto zakotwienie dwiema śrubami M25, na głębokości L=(20-30d)=(500-750)mm, przyjęto L=550mm

3.0 Obliczenie głowicy słupa:

3.1 Przyjęcie wymiarów poziomej płyty głowicy.

Przyjęto wymiary:

L=500mm

B=400mm

tp=20mm

3.2 Obliczenie blachy trapezowej.

Założono grubość blachy trapezowej bt=14mm

-Wyznaczenie wysokości blachy trapezowej

Przyjęto grubość spoiny a=5mm (z pkt. 2.2.1)

-wysokość blachy trapezowej

τ=N/a*∑l ∑l=4ht

α║=0,8 fd=215MPa

τ=RB/a*4ht<α║*fd →ht>RB/(a*4* α║*fd)

ht>1155,45/(0,005*4*0,8*215000)=0,336m

Przyjęto wysokość blachy trapezowej ht=0,35m

-Wyznaczenie szerokości blachy trapezowej:

Lt=B=400mm

Przyjęto blachę trapezową: 400*350*14mm

3.3 Wymiarowanie łożyska podporowego.

Wyznaczenie grubości łożyska:

-wyznaczenie maksymalnej wartości momentu gnącego:

S=L-2*4=50-8=42cm

L=hc280+bt=0,28+0,014=0,294mm

q= RB/B=1155,45/0,4=2888,625kN/m

MMAX=25,4777kNm

-grubośćłożyska

tc=t1+tp → t1= tc - tp

tc = √(6*MMAX/b1*fd)=6*25,5/(0,12*205000)=0,09m

t1=0,09-0,02=0,07m

-obliczenie promienia łożyska:

σbH=0,42*√(p*E/r)<fdbH=3,6fd →r>p*E/((3,6fd/0,42)²)

p=q=2888,625kN/m

r>2888,625*205*10^6/(3,6*205000/0,42)²=0,192m<rmin=0,5m

→Przyjęto łożysko podporowe: 120*420*70mm o promieniu r=500mm

-Sprawdzenie docisku łożyska do blachy podłożyskowej:

σd=RB/b1*d1=1155,45/0,12*0,42=22,925<1,25*205=256MPa

WNIOSEK:

Wytrzymałość blachy podłożyskowej na docisk jest wystarczająca:

3.4. Obliczanie spoin w głowicy słupa.

3.4.1. Spoiny pionowe

Jak w punkcie 3.2

3.4.2 Spoiny poziome.

-wyznaczenie grubości spoiny z warunków konstrukcyjnych

0,2t2<10mm<anom<0,7t1

2,5mm< anom<16mm

t1=14mm

t2=20mm

0,2*20=4mm< anom<0,7*14=9,8mm

2,5mm< anom<16mm

-Przyjęto grubość spoiny a=7mm

-Wyznaczenie naprężeń stycznych prostopadłych spoiny:

τ┴=RB/a*∑l<α┴*fd

∑l=2*B+4*a2=2*0,4+4*0,0597=1,0388m

τ┴=1162,242/(0,007*1,0388)=159833kPa< α┴*fd=0,9*205000=184500kPa

WNIOSEK: Nośność spoiny jest wystarczająca.

1

---