6. Zachowanie się układów prętowych przy obciążeniach termicznych i geometrycznych.

7. Obciążenia różnych typów; wpływ temperatury, przemieszczenia wymuszonego, uwzględnienie sprężystego podparcia punktowego i ciągłego, wykorzystanie symetrii układu i obciążeń.

I.Typy obciążeń:

• statyczne - wartość zwiększa się od zera do wartości końcowej,usuwanie obciążenia na statyczne można związać z największym okresem drgań własnych konstrukcji.Jeżeli czas zmiany obciążenia jest znacznie większy od największego okresu drgań własnych konstrukcji,to można to nazwać statycznym

• dynamiczne - wartość zmienia się nagle lub okresowo zmiennie lub w chwili przyłożenia do konstrukcji jest skończona

Zależnie od czasu trwania i sposobu działania:

• stałe - wartość,kierunek i położenie pozostają niezmienne w czasie użytkowania budowli,jej montażu i remontu

• zmienne - mogą zmieniać wartość,kierunek lub położenie w czasie użytkowania budowli

-w całości długotrwałe- np.parcie wody o stałym poziomie zwierciadła

-w części długotrwałe- np.ciężar pyłu,obciążenie od suwnic

-w całości krótkotrwałe- np.śnieg,wiatr

• wyjątkowe - występują w wyniku mało prawdopodobnych zdarzeń w czasie użytkowania budowli (powódz,pożar)

II.Wpływ temperatury

Zmiana temperatury w stosunku do temperatury montażu powoduje wydłużenie pręta w osi lub :zginanie pręta momentami powstałymi na skutek gradientu temperatur.

Siły wewnętrzne powstające pod wpływem tego rodzaju obciążenia można obliczać za pomocą metody przemieszczeń, gdzie zadane przemieszczenie wynosi α*t*l,

α- współczynnik rozszerzalności termicznej

t - temperatura

l - długość pręta

lub metodą sił, w której wpływ temperatury uwzględniony jest przez Δ_it

δ₁₁x₁ + δ₁₂x₂ + Δ_1t = 0

δ₂₁x₁ + δ₂₂x₂ + Δ_2t = 0

Δ_it = Σ [ ∫N_i*α*t_c*ds. + ∫M*α*(ΔT/h)ds. ]

h - wysokość przekroju

∫N_i*α*t_c*ds. - równomierne ogrzanie

∫M*α*(ΔT/h)ds. - nierównomierne ogrzanie

III.Wymuszone przemieszczenie

Siły wewnętrzne w układzie statycznie niewyznaczalnym,wynikłe z przemieszczenia podpór wylicza się za pomocą:

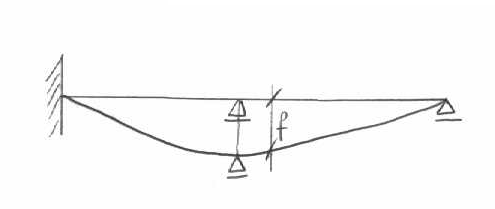
• metody przemieszczeń - przemieszczenie podpór f traktuje się jako obciążenie geometryczne stanowi osiadanie podpór lub wymuszone przemieszczenia węzłów

• metody sił - układ równań:

gdzie Δ_ip = 0 - brak obciążenia zewnętrznego

x₁δ₁₁ + x₂δ₁₂ + Δ_1p = -f

x₁δ₂₁ + x₂δ₂₂ + Δ_2p = 0

---