Mostek rezystancyjny

I. Wstęp.

Pomiary przy użyciu mostka rezystancyjnego są powszechnie stosowaną metodą pomiaru rezystancji, indukcyjności i pojemności.

Samo słowo „mostek” oznacza w tym przypadku fakt, iż w pomiarach tego typu dwa punkty obwodu są połączone przez wskaźnik zrównoważenia (przyrząd mierzący prąd lub napięcie), który ma za zadanie wykryć różnicę potencjałów między tymi punktami, w szczególnym przypadku zerową.

Najprostszą formą mostka jest czteroramienny mostek rezystancyjny Wheatstone'a, zasilany ze źródła napięcia stałego.

Mostek może być używany w dwóch układach:

• zrównoważonym ( zerowym)

mamy wówczas do czynienia z zerową różnicą potencjałów między punktami A i C mostka;

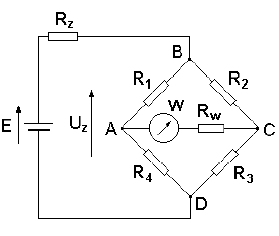
Oznaczenia:

 E - SEM źródła

 Rz - rezystancja wewnętrzna źródła

 W - wskaźnik zrównoważenia mostka

 Rw - rezystancja wewnętrzna wskaźnika

Rys. 1. Schemat mostka Wheatstone'a do pomiaru

rezystancji.

W stanie równowagi mostka (Uwy=UAC=0) jest spełniony warunek:

R1/(R1 + R4) = R2/(R2 + R3),

a stąd po przekształceniu otrzymuje się warunek równowagi mostka:

R1R3=R2R4.

Warunek równowagi nie zależy od rezystancji wewnętrznej Rz źródła zasilającego mostek, ani też od czułości i rezystancji wejściowej Rw wskaźnika zera.

Wymienione czynniki warunkują jednak precyzję, z jaką można stan zera określić.

Czułość S mostka można zdefiniować jako stosunek napięcia wyjściowego mostka do napięcia zasilania, tj.

S = Uwyj/Uz.

Czułość mostka zależy od rezystancji źródła i wskaźnika, a także od stosunków rezystancji poszczególnych ramion mostka.

Mostek o jednakowych ramionach jest najbardziej czuły na zmiany rezystancji.

- niezrównoważony ( wychyłowy)

między punktami A i C występuje niezerowe napięcie lub prąd, a jego pomiar realizujemy przy pomocy wskaźnika.

Mostek niezrównoważony (wychyłowy) stosuje się wtedy, gdy trzeba w sposób ciągły mierzyć (a najczęściej również rejestrować) małe zmiany rezystancji ( δ1).

Posługując się mostkiem wychyłowym należy pamiętać, że:

 napięcie wyjściowe mostka wychyłowego zależy wprost proporcjonalnie od wartości napięcia zasilania mostka;

dla małych wartości rozrównoważenia mostka napięcie wyjściowe mostka zależy prawie liniowo od rozrównoważenia - nieliniowośc wzrasta ze wzrostem δ;

 w praktyce często stosuje się doświadczalne wzorcowanie mostka wychyłowego za pomocą rezystora kalibracyjnego dołączonego równolegle do rezystora wzorcowego R2.

Typowym zastosowaniem mostka Wheatstone'a są pomiary rezystancji w zakresie od 1Ω do10 MΩ.

II. Cel ćwiczenia.

Realizowanym zadaniem jest zapoznanie się z mostkiem Wheatstone'a do pomiaru rezystancji oraz jego właściwościami w zastosowaniach jako mostek zrównoważony i wychyłowy.

III. Wykorzystane przyrządy.

1.Mostek Wheatstone'a

2.Opornica dekadowa

3.Woltomierz cyfrowy Metex

4.Źródło o E = 4,5V.

IV. Wykonanie ćwiczenia.

1.1

Do mostka (rys. 1) dołączam jako R1 dekadę rezystancyjną i zrównoważam nią mostek kolejno dla

R2=100Ω oraz R2=1kΩ, przy różnych wartościach stosunku R4/R3 (1, 10, 0.1). W każdym przypadku

określam najmniejszą możliwą do uzyskania zmianę wskazania wskaźnika zrównoważenia mostka

1.3

Do mostka dołączono jako R1 dekadę rezystancyjną, nastawiono R2=R3=R4=100Ω i zrównoważono mostek utrzymując stałą wartość napięcia zasilania równą 4,5V.

Mierzono napięcie wyjściowe mostka w funkcji stosunku Rx/R0, gdzie R0 jest wartością rezystora w stanie zrównoważenia mostka.

W naszym ćwiczeniu R0=100Ω.

Stosunek Rx/R0 zmieniano w sposób równomierny, w granicach 0,2÷2 oraz0,9÷1,1.

Wartości zmierzone przy pomocy woltomierza zestawiono w tabeli i na ich podstawie sporządzono wykresy U_AC=f(Rx/R0).

Tabela 1.1

.

Lp	R1[Ω]	R2[Ω]	R3[Ω]	R4[Ω]	R4/R3	Uwyj[mV]	ΔR	ΔUac[mV]
1	100	100	100	100	1	0,41	0,1	1,1
	100,1					1,51
2	1000,1	100	100	1K	10	-0,08	0,1	0,1
	1000,2					0,02
3	9,9	100	1K	100	0,1	-2,43	0,1	3,64
	10					1,21
4	1000,3	1K	100	100	1	0	0,1	0,03
	1000,4					0,03
5	10002	1K	100	1K	10	-0,01	0,5	0,01
	10002,5					0
6	99,9	1K	1K	100	0,1	-0,73	0,1	1,1
	100					0,37

Tabela 1.3 a

Wartości U_AC dla stosunków Rx/R0 zmienianych w granicach 0,2÷2.

Lp	Rx	Uac[V]	Rx/Ro
1	20	-1,4552	0,2
2	30	-1,1771	0,3
3	40	-0,9381	0,4
4	50	-0,7304	0,5
5	60	-0,5483	0,6
6	70	-0,3873	0,7
7	80	-0,2439	0,8
8	90	-0,1155	0,9
9	100	0,00037	1
10	110	0,10548	1,1
11	120	0,2006	1,2
12	130	0,2878	1,3
13	140	0,3679	1,4
14	150	0,4416	1,5
15	160	0,5096	1,6
16	170	0,5726	1,7
17	180	0,6312	1,8
18	190	0,6859	1,9
19	200	0,7369	2

wykres 1.3a

Tabela 1.3b

Wartości U_AC dla stosunków Rx/R0

Lp	Rx	Uac[V]	Rx/Ro
1	90	-0,1154	0,9
2	91	-0,1034	0,91
3	92	-0,0913	0,92
4	93	-0,0795	0,93
5	94	-0,0678	0,94
6	95	-0,0561	0,95
7	96	-0,0446	0,96
8	97	-0,0332	0,97
9	98	-0,022	0,98
10	99	-0,0108	0,99
11	100	0,002	1
12	101	0,0111	1,01
13	102	0,022	1,02
14	103	0,0327	1,03
15	104	0,0433	1,04
16	105	0,0539	1,05
17	106	0,0643	1,06
18	107	0,0746	1,07
19	108	0,0848	1,08
20	109	0,095	1,09
21	110	0,1052	1,1

wykres 1.3b

V. Wnioski

Dla podpunktu 1.1 widzimy ,że w zależności ustawienia rezystancji R2,R3,R4 możemy uzyskiwać rożne efekty, np. dla pomiaru 5 na piec ziaren rezystancji uzyskujemy tylko jedno ziarno ΔUac, co oznacza ze przy tym ustawieniu nasz przyrząd pomiarowy jest nie dość czuły, natomiast dla pomiaru 3 , na jedno ziarno rezystancji uzyskujemy 36 ziaren ΔUac, co oznacza ze dla tego ustawienia aparat pomiarowy ma bardzo dużą czułość. Tworząc odpowiedni układ możemy mierzyć nawet najmniejsze różnice napięcia , co daje nam możliwość tworzenia bardzo czulej aparatury pomiarowej, np. termometry wykorzystujące efekt zmiany rezystancji materiału pod wpływem temp ,także pH metry i szereg innych urządzeń do pomiarów rożnych sygnałów .

5

---