Nr ćwiczenia |
Wyznaczanie rozkładów wyników pomiarów (krzywa Gaussa) wykonanych przy użyciu mostka Wheatstone'a. |
Ocena przygotowania teoretycznego. |
|||
1 |
|
|
|||
Nr zespołu |
Nazwisko i imię |
Ocena za sprawozdanie. |
|||
9 |
Bieszczad Paweł |
|
|||
Data |
Wydział |
Rok |
Grupa |
|
UWAGI : |
11.04.2000 |
EAI i E |
I |
I |
|
|
Cel ćwiczenia:
Wykazanie statystycznego charakteru wyników pomiarów przy użyciu mostka Wheatstone'a.
Wiadomości teoretyczne:
Z błędem przypadkowym mamy doczynienia, gdy występuje statystyczny rozrzut wyników kolejnych pomiarów wokół wartości średniej.
Błędy systematyczne Wynikają one ze złego cechowania ( kalibracji) przyrządów pomiarowych, z błędnej metody pomiaru lub z działania czynników zewnętrznych.
Błędy grube powstają na skutek nieumiejętności użycia danego przyrządu, pomyłek przy odczytywaniu i zapisywaniu wyników itp.
W większości doświadczeń stwierdza się, że rozkład błędów przypadkowych jest dany jako rozkład Gaussa.
Prawo Ohma - Opór rozważanego przewodnika jest zawsze taki sam, niezależnie od wielkości przyłożonego napięcia w celu zmierzenia go. U=IR
Prawo to nie stosuje się jednak do wszystkich przewodników. Dla wszystkich słuszny jest jednak: ![]()
Prawa Kirchhoffa to dwa podstawowe prawa dotyczące przepływu prądu stałego w obwodach:
I prawo Kirchhoffa: wektorowa suma wszystkich natężeń prądu dopływających do punktu rozgałęzienia w obwodzie elektrycznym równa jest zeru (inaczej: suma natężeń prądów wpływających do punktu rozgałęzienia równa jest sumie natężeń prądów wypływających).
II prawo Kirchhoffa: suma spadków napięcia w każdym zamkniętym obwodzie elektrycznym równa jest zewnętrznej sile elektromotorycznej SEM działającej na ten obwód.
Błąd średni kwadratowy pojedynczego pomiaru.
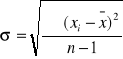
Błąd średni kwadratowy średniej arytmetycznej.
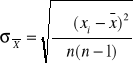
Rozkład Gaussa.
W tym rozkładzie funkcja gęstości jest następująca
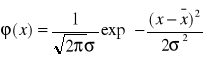
Wzór na nieznany opór mostka Wheatstone'a.
Gdy mostek jest w stanie równowagi to przez galwanometr nie płynie prąd. Oznacza to, że przez Rx i R1 płynie prąd o takim samym natężeniu oraz, że spadki napięć na Rx i R2 są takie same. Korzystając z tego możemy obliczyć Rx.
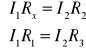
czyli ![]()
Zastępując rezystancję R2 i R3 działkami, których liczba jest wprost proporcjonalna do rezystancji otrzymujemy: Rx =
Pomiary:
Znaczny wpływ na dokładność pomiarów ma dokładność helipotu.
Opór dekadowy nie ma praktycznie wpływu na ten błąd.
Jak widać z powyższych obliczeń wyliczona procentowa zawartość wyników w odpowiednich przedziałach jest zbliżona do teoretycznych
Średnia ważona i średnia arytmetyczna mają tę samą wartość
Pomiar oporu mostkiem Wheatstone'a daje dość dokładną wartość mierzonego, nieznanego oporu, ponieważ wpływ na błąd ma tylko dokładność jednego przyrządu
Wyszukiwarka
Podobne podstrony:
Lepkość-sciaga, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[4]tabelka, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYK~47, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
cw8 wyniki, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
za, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki fizy
konspekt nr8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fi
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
konspekt 8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
konspekt 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
rys, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 11 Poziomy energetyc
więcej podobnych podstron